ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
1-2.エジプト数学と歴史観の変遷
ページ目次
記数法から見る数の理解
現代の私たちは、歴史書を読むとき、どうしても現代人の考え方や道徳観で過去の出来事を判断してしまいます。しかし古代の人たちは現代の私たちとまったく違ったものの見方をしていることが多いのです。これは神話とか昔話を読むときも時々感じます。ただし、神話や昔話などの伝承は、その時代の感性に合うようにどんどん書き換えられてしまっていることにも注意が必要です。歴史上の出来事も時代によって解釈がずいぶんと変わってきます。ある高名な歴史学者は「歴史は歴史学者の創作である」といっています。
では数はどうでしょうか。数はこれまでどのように考えられ、どのように扱われてきたのでしょうか。
数にはいろいろなものがあるので、ここで復習しておきましょう。ものの個数を数える、1, 2, 3, … を自然数といいます。自然数にゼロと負の数を加えたものが整数です。分母と分子がともに整数である分数が有理数です。有理数以外の実数を無理数といいます。もちろんこれは自然数、整数、有理数、無理数の定義ではありません。昔の人は、数というものは自然界にもともとあるものと考えていて、定義をしようなどとは考えもしませんでした。これに関しては次の問いがよく知られていて、多くの著作で引用されています。
数は人間の発明か、それとも人間などいなくても存在したのか
19世紀も終わりごろになって、クロネッカー※という数学者は次のように言っています。

自然数は神がお創りになった。それ以外は人間の業だ。
しかし、このすぐ後にペアノ※という数学者が自然数までも定義してしまったのです。
サルやイルカ、カラスやオウムなども数を認識するといいます。でもこれは小さな数にすぎません。億とか兆、あるいはもっと巨大な 1050 とか 10100 といった数はどうでしょうか。こういった数を理解するには言語や記号が必要です。私たちは言語を使ってものを考えます。言語がなければ思考は非常に制限されたものになるでしょう。言葉は文字によって記録されます。しかし、文字は単に言語を記録するだけのものではありません。文字の発明によって、言語は急速に発展したのです。このことは、数をどのように記号化するかという記数法をみても分かります。つまり、古代の人々の『思考』を知るためには、その時代の言語や扱っていた文字の理解が不可欠なのです。
ヨーロッパの人々は、近世になるまでローマ数字を使っていました。ローマ数字は古い時計などに使われている数字で、たとえば 1, 2, …, 11, 12 は
I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII
と表されます。これは文字を覚えることが苦手な当時の一般大衆が使うのにはよかったのですが、億とか兆といった大きい数字を表すのはとてもできませんし、扱うことができるのは自然数だけでした。レオナルド・ダ・ヴィンチ※が活躍するルネサンスになると、アラビアから入ってきたアラビア数字(現在私たちが使っている算用数字 0, 1, 2, …, 9)とそれを用いた10進数が使われるようになりますが、扱われるのは依然として自然数だけだったのです。つまり、ルネサンス期まではヨーロッパには分数も小数もなかったのです。ですから、古代人もルネサンス期の人々も円周率 π = 3.14… とか、黄金率 φ = 1.618… などという概念は持っていなかったはずです。
ギリシア数学とオリエントの影響
ヨーロッパの人たちの歴史観には、ギリシアが大きくかかわっています。ギリシアはヨーロッパ文明の源流、数学はギリシアで生まれたとされてきました。しかし最近、エジプトのパピルスの象形文字や、メソポタミアの楔形文字の解読が進み、古代オリエント文明にも高度な数学が存在していたことが明らかになってきました。ギリシアの数学はオリエントの数学の影響を受けている可能性があるのです。つまり、ギリシア文明は、東地中海を取り巻く地域全体の文明の一部として考えられるようになってきたのです。
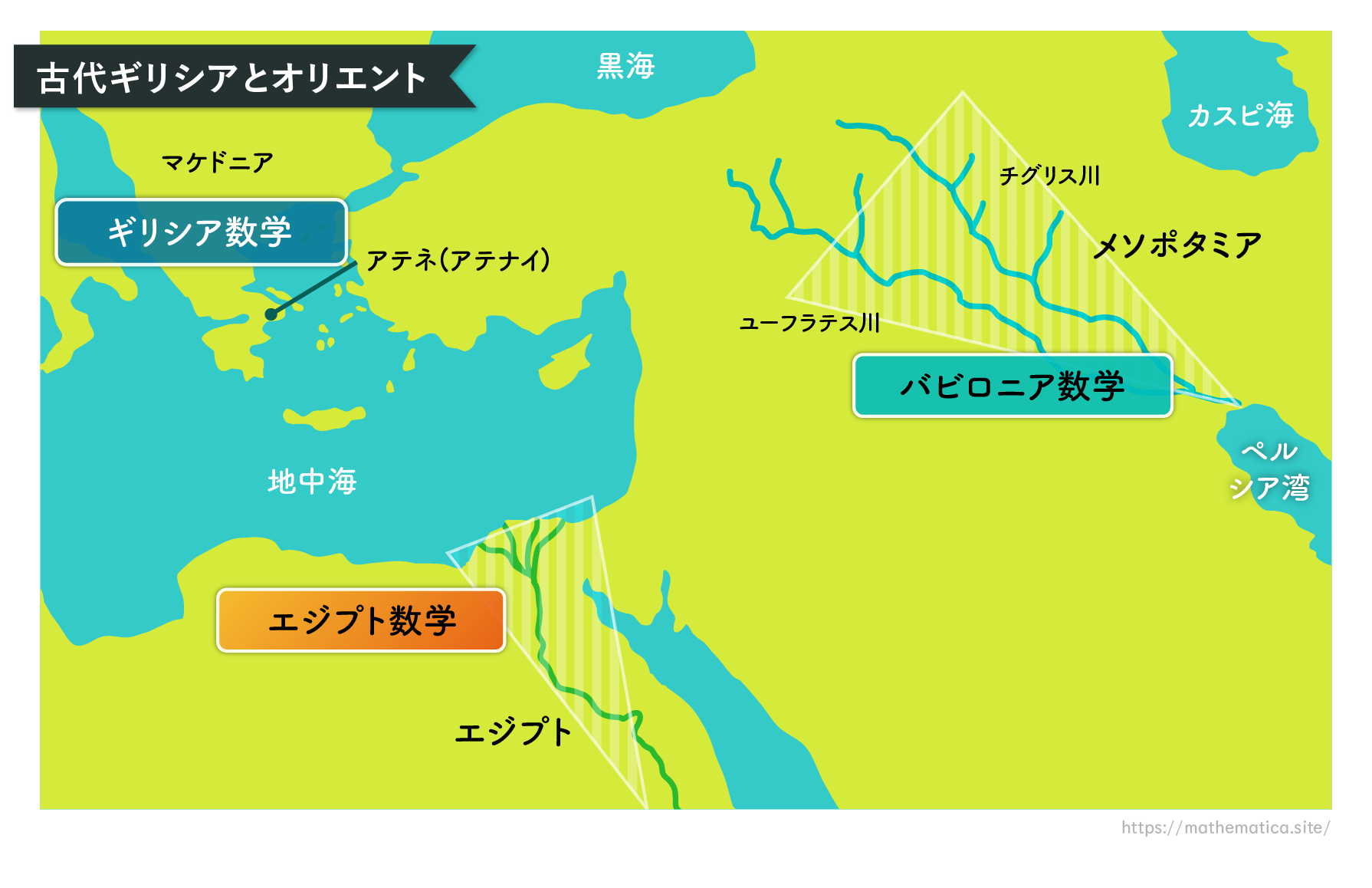
メソポタミア地方で発達した数学を「バビロニア数学」とよぶのが慣習となっていますから本連載でもこの呼び方をします。ここで、エジプト数学、バビロニア数学、ギリシア数学、について少し述べます。エジプト文明の最後の王朝はギリシア人の王が支配する王朝でした。したがって本連載で用いる用語の多くはギリシア語です。最近の専門の歴史書とか数学史の本などは、古代エジプト語を用いることが多くなっているようですが、本連載は基礎的な数学史を扱いますので、一般に使われている用語を使うことにしました。また、たとえばファラオなどの用語は、ピラミッド時代ではまだ使われてなく、それよりあとの時代に使われるようになったようですが、時代を通してエジプト王のことをファラオと呼びます。
エジプト文明とギリシア文明
ギリシア文明が興ろうとしていたころエジプト文明は長い歴史の黄昏期に入っていました。ギリシア本土は山がちで農地が少なく、農業だけでは食べていけません。地中海沿岸都市と交易をしたり、植民地を作って移住をします。特にアナトリア(現在のトルコ)にはギリシアの植民都市がいくつもできました。当時の交易は、時として略奪行為に変貌します。老人は殺され、子供や若者は奴隷にされます。しかし古代では、このような行為は当たり前のことで、非難されるようなことではなかったのです。ギリシア人は勇猛さは定評があり、各地で傭兵として雇われていました。あるときエジプトのある海岸の村がギリシア人の一団に襲われました。それを聞いたファラオは急いで駆けつけ、ギリシア人と交渉し、エジプトの傭兵として雇い入れることで話はまとまります。エジプトにギリシア人の傭兵の町ができ、その町を仲介としてギリシアとの交易が始まります。
ギリシア古典期・ヘレニズム時代・ローマ時代
当時メソポタミアには、エジプトと同じぐらい古い歴史を持つ文明が栄えていました。なかでも古都バビロンを首都とするバビロニアは巨大な城壁に囲まれた文化都市で、多くの商人が行き交い国際都市として栄えていました。ところが、メソポタミアの深部で興ったペルシアが次々と周りの国を平定して、ついにはバビロニアも滅ぼし大帝国に成長してきます。
ギリシアも、東地中海沿岸にいくつもの都市を持つまでに成長していましたが、まだまだペルシアに対抗できるだけの力はありませんでした。ギリシア人はエーゲ海をわが海として活動していましたが、とうとうペルシア戦争が勃発します。そのとき奇跡が起こります。都市の連合体にすぎないギリシアが、だれもが負けると思っていたギリシアが、大帝国ペルシアに勝ったのです。このペルシア戦争の勝利から、ギリシアの都市連合体が北のギリシアの小王国マケドニアに敗北するまでを、ギリシアの古典期といいます。ギリシアの古典期はギリシア文明が華やかに花開いた時期であり、文芸、彫像、建築などの“ヨーロッパの古典”がこの時代に発達したのです。
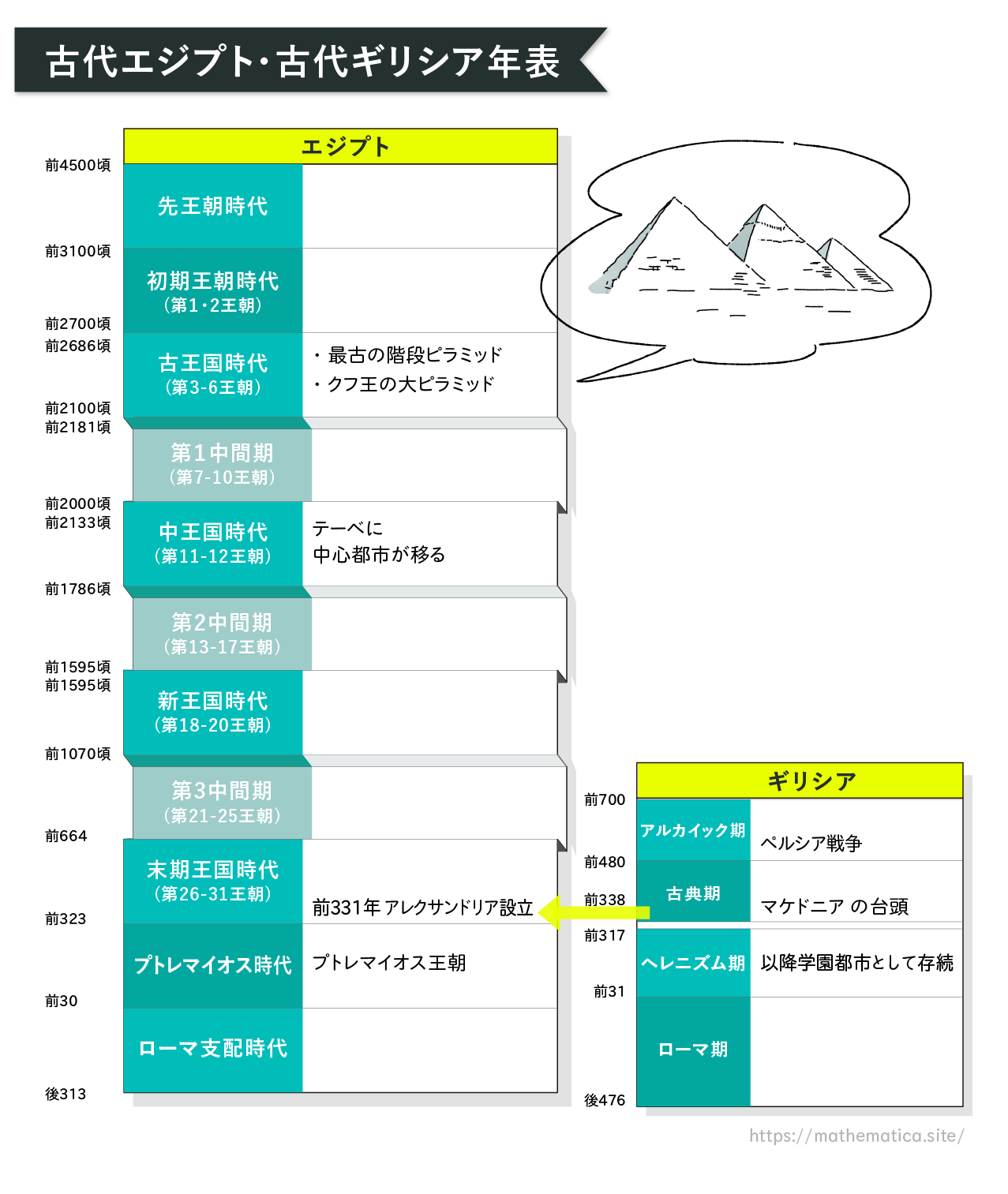
マケドニアの王アレクサンドロス※は、ペルシア戦争の報復という名目でペルシア征服の遠征を開始し、ついにペルシア帝国を滅ぼし大帝国を樹立します。エジプトにはアレクサンドリアという都市を建設します。しかしアレクサンドロス大王はあっけなく死んでしまい、帝国は分裂します。
エジプトには、アレクサンドロス大王の将軍の一人プトレマイオスがエジプト王朝を引き継ぎ、プトレマイオス王朝をひらきます。このときから、エジプトがローマに征服されローマの属州となるまでをヘレニズム時代と呼びます。ヘレニズム時代のあとはローマ時代です。
古典期のギリシア人と高度なエジプト数学
最近まで古代エジプトに高度な数学が発達していたことは知られていませんでした。知られていなかったというよりは、忘れ去られていたといった方がいいかもしれません。古典期のギリシア人はエジプトの進んだ文化を認めていて、多くの哲学者や政治家がエジプトの先進科学や社会システムを学びに訪れています。歴史の父ヘロドトス※もエジプトを訪れ、エジプトの進んだ文化に驚嘆し、ギリシアは神々をはじめ多くのものをエジプトから学んでいることを認めています。
ローマ時代のあとはイスラーム世界の支配を受け、さらに近世に入ると、ヨーロッパ列強の植民地主義の犠牲となります。近世のヨーロッパの科学技術の発達はすさまじく、ヨーロッパは先進国、エジプトを含むアジアは後進国とみなされるようになりました。もはやエジプトに進んだ数学が存在したなどとは誰も思わなくなってしまったのです。
エジプト数学・バビロニア数学・ギリシア数学の特徴
ギリシア数学、バビロニア数学、エジプト数学の特徴と違いを整理しましょう。これまで現代数学の源流はギリシアにあるとされてきました。ギリシア数学では、理論を展開する前にまずどのような前提で議論するかをはっきりさせます。つまり、だれもが正しいと認めることを公理(“公準”ともいいます)として述べます。次に理論のなかで使用する用語の意味を明確にします。これを用語の定義といいます。さらに、明確な定められた推論形式にのっとって論証を進めます。この過程を証明といいます。このような『公理』『定義』『証明』で構成される数学を論証数学といい、これらは現代数学に引き継がれています。これに対し、エジプト数学やバビロニア数学などオリエントの数学には「なぜ成立するのか」ということを示す明確な証明というものがありません。批判的に見る人はこれを、「単なる実用の具であるとか、職人芸にすぎない」と、たいして価値を認めてきませんでした。また、扱っている対象や目的から見ると、ギリシアは理論数学、オリエント(エジプト数学・バビロニア数学)は実用数学ということができます。この対立はまた、純粋数学対応用数学と言い換えられることがあります。
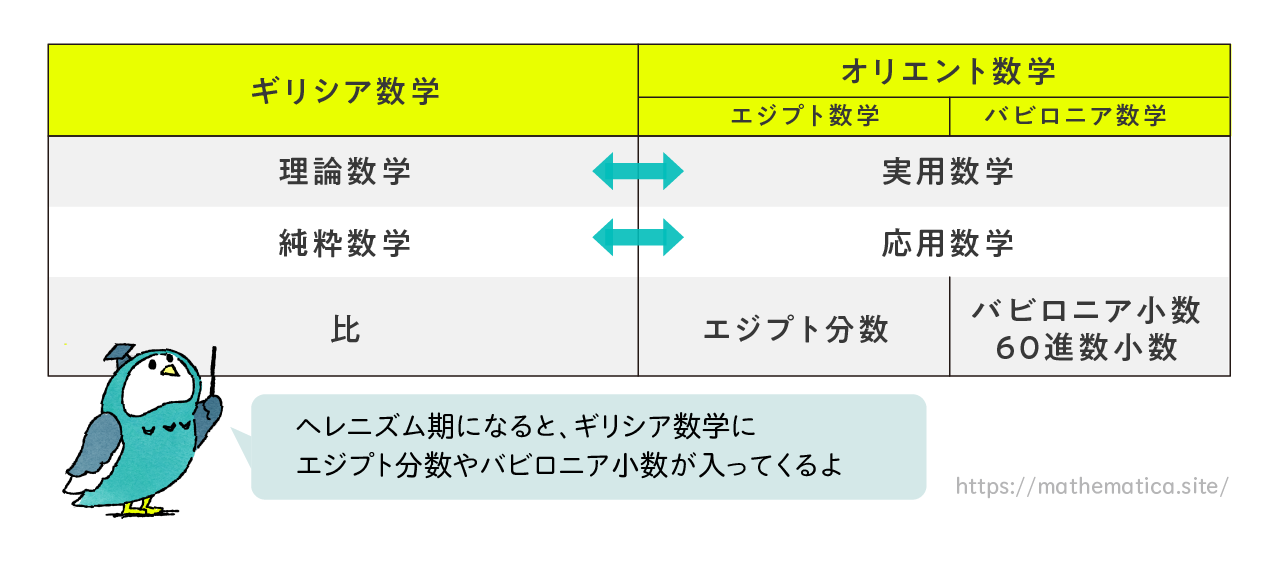
数についてもエジプト数学、バビロニア数学、ギリシア数学では扱いが違います。エジプトではエジプト分数とよばれる特殊な分数を使っていました。エジプト分数については別の記事で詳しく解説したいと思います。バビロニアでは60進数小数とよばれる特殊な小数を使っていました。60進数小数は、現在の私たちも時間や角度を表すのに使っています。たとえば
23度45分18秒 = 23°45’18” = 23 + 45 60 + 18 3600 度 = 23.755 度
古代ギリシアでは比を扱います。注意しなければならないのは「比は数ではない」ということです。現在の私たちは、比「a 対 b」を分数a bと同等のものとして扱っていますが、もともとは別の概念なのです。たとえば「3 対 5」という比は「私の年齢に対する兄の年齢は 3 に対する 5 という比に等しい」という表現の中でしか用いられません。言い換えると、ギリシア数学における比の表現では必ず4つの数が現れ、「3 対 5」とか「私の年齢対兄の年齢」が別々に扱われることはなかったのです。一方これを分数で表すと、「兄の年齢はわたしの 5 3倍」あるいは「私の年齢は兄の 3 5倍」となり、5 3 や 3 5 がひとつの対象、つまり分数という数として認識されるようになります。3 5 という分数は「3を5で割る」という行為を表しますが、同時にその結果である 0.6 という数値を表します。現在の私たちは「a 対 b」という比を a : b という式で表します。すると「a:b」という表現自体が一つの抽象的な対象を表すようになってきます。分数と比が同一視されるようになったのは、数学に式が使われるようになった近世に入ってからです。つまり、ギリシア人にとって、比とは2つの対象 a と b の関係を表すものであって、現代の式 a : b とか a b のような一つの対象を表すものではなかったのです。
時代とともに変わる数の概念
エジプト人は分数(正確にはエジプト分数)を、バビロニア人は小数(正確には60進数小数)を数としていました。これに対し、ギリシア人が考える数とは自然数でした。長さ、面積、体積、角度などは量として扱っており、数とは区別していたのです。たいていの古代文明では長方形の面積を「縦の長さ×横の長さ」と計算しますが、ギリシア数学ではこのような扱いはしていません。でも逆に考えて、私たちはなぜ「長方形の面積=縦の長さ×横の長さ」と計算できるのでしょうか。
ここでいうギリシアの数とは、正確にはユークリッド※の『原論』で扱われている数のことです。ヘレニズム期になると、ギリシア数学にエジプト分数やバビロニアの小数が入ってきます。有名なヘレニズム期やローマ期の数学者アルキメデス※、ヘロン※、プトレマイオス※などはエジプト分数を使って面積の計算をしています。(アルキメデスは、エジプト分数も、バビロニア小数も両方使っています。)
古典期のギリシアでも、商人や農民や建築技師などは、実用的に布や畑や土地などの面積を「長さ×長さ」で計算したはずです。ではなぜギリシアの数学者は長方形の面積を「縦の長さ×横の長さ」と定めることをしなかったのでしょうか。ギリシア数学は純粋数学であって実用数学ではなかったからです。ギリシア人数学者にとって“長さとは何か”、“面積とは何か”、“掛け算とは何か”などを定義することは必要なかったのです。
現在の私たちであれば「長さとは正の実数のことである」と定義できます。しかし、実数が厳密に定義されたのは19世紀に入ってからのことです。数、長さ、面積などの正確な定義は実は大変難しいのです。
以上をまとめると、数という概念も普遍的なものではなく、エジプトとバビロニアとギリシアでは違っていたようなのです。また時代によっても扱う数の概念は変わってきます。バビロニアでは分数を扱っていましたが、無限小数などはありませんでした。いずれにしても、古代やルネサンス時代の人々の頭には円周率 π = 3.1415… とか黄金率 φ = 1.618… という数はありませんでした。
これまで円周率 π について議論してきました。アルキメデスが π の近似値として 22 7 を得たことは有名です。アルキメデスは 22 7 が「 π の真の値」ではないことは知っていたと思います。さらにもっと正確な値が計算できることも知っていたでしょう。しかし果たしてアルキメデスは「円周率 π の真の値はなにか」などということを考えたでしょうか。皆さんはたとえば鉛筆を見て「この鉛筆の真の長さはなにか?」などと考えますか。
小数点以下たった 10 桁で原子の大きさを越えてしまいます。 π の値は計算を無限に続けたその先にある値です。人類が「 π の真の値」に興味を持つようになるのは、数学がもっと進んでからのように思います。人間は必要でないことには思いが至らないものです。したがって、以下本連載では円周率と黄金率は、 π および φ のことではなくて、 π の近似値、 φ の近似値を意味することにします。前回の1-1.ピラミッドの謎とは でも述べた円周率の謎も微妙に意味が違ってきます。
円周率の謎大ピラミッドの底面の周長を高さの 2 倍で割ると円周率になる
周長も高さも共に測定値ですから近似値であり、当然計算結果も近似値となります。したがって、円周率が π の近似値でなく π 自身だとすると、いくら精確に大ピラミッドを測っても「ピラミッドの謎」を解くことはできません。些細なことのようにも思いますが、はっきりさせておきます。
