ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
4-6.古代ローマとルネサンス:ウィトルウィウスと実用数学
ページ目次
ギリシアの数学の変遷:古典期からヘレニズム期、そしてローマ期への移り変わり
『4-4.古典期の数学とヘレニズム期の数学』でギリシアの古典期の数学とヘレニズム期の数学の違いを述べ、『4-5.アルキメデスの円周率 』では具体的な例として、アルキメデス※の円周率の計算を見てみました。ここではもう一度振り返って、古典期からヘレニズム期、ローマ期とどのように移り変わっていったかを見てみましょう。
アテナイの学園都市とギリシアの古典文化の守護
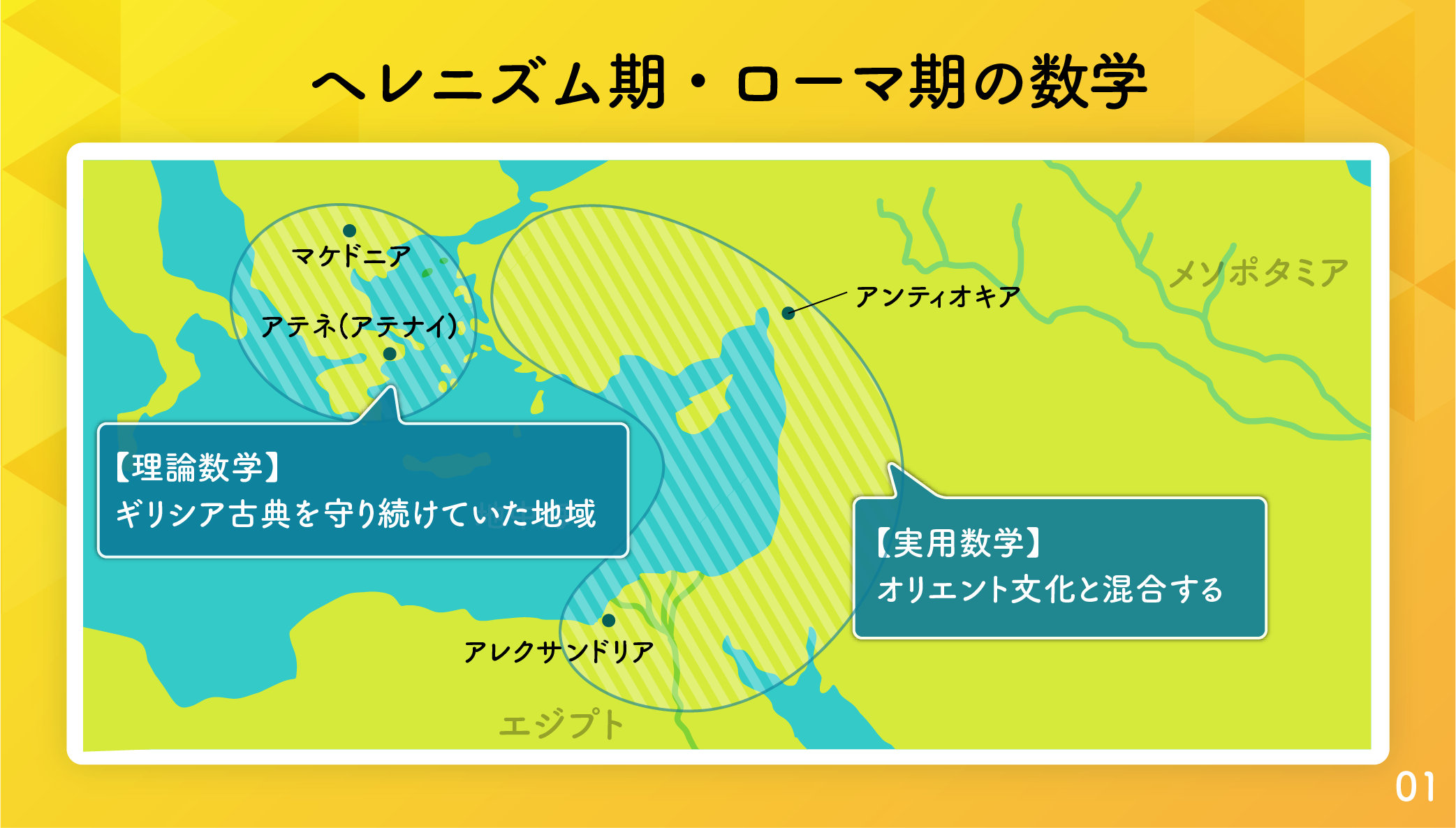
ギリシア史のある専門家は、ヘレニズム期のギリシア文化圏を「旧 いギリシア」と「新しいギリシア」の2つに分けることができる、と述べています。「旧いギリシア」とはギリシア本土と、エーゲ海の島々のことで「新しいギリシア」とは新たに支配したエジプトやシリアやメソポタミアなど、豊かなオリエント文明の遺産を引き継ぐ地域のことです。「新しいギリシア」はエジプトのアレクサンドリアやシリアのアンティオキアを中心として活発な交易活動を開始し、文化の先進地域となります。新しい血が入ったため、ギリシア文明も若さを取り戻し、再生します。一方「旧いギリシア」であるギリシア本土は、もともと農作に適さない痩せた土地であったうえに、大国の間にあって相変わらず紛争や政変が繰り返されて、経済も疲弊し、新しい潮流から取り残されていきます。
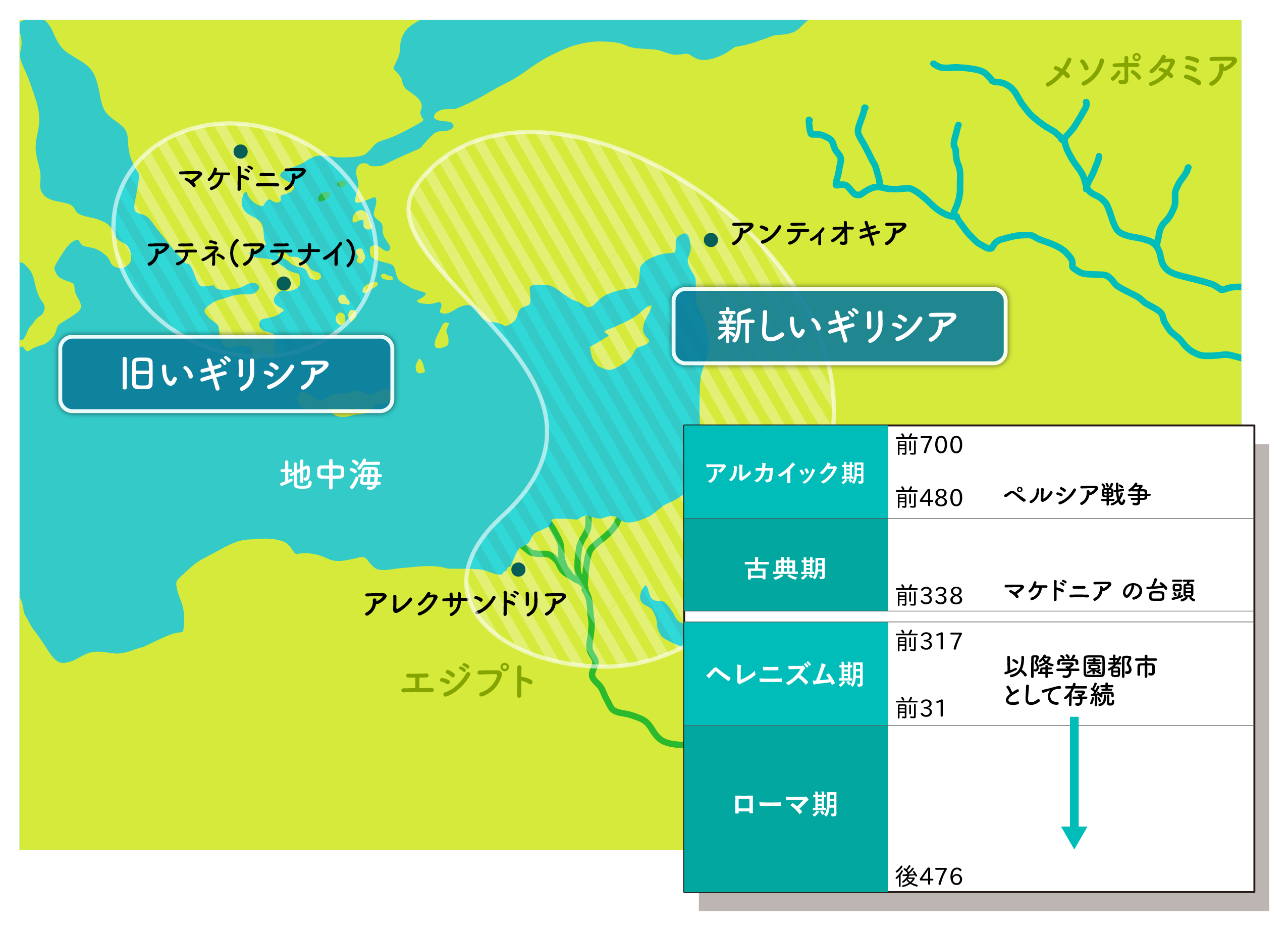
ローマは、紀元前4世紀ごろまではイタリア半島中部の小さな都市国家にすぎませんでしたが、しだいに勢力をのばしてきて、やがて東地中海地域はローマに支配されることになります。ローマ時代になっても、「旧いギリシア」と「新しいギリシア」はそのまま存続します。
「旧いギリシア」に属するアテナイは、かつての裕福なポリスではなくなっていましたが、「学園都市」として存続していました。プラトン※の創った教育と研究の学園アカデメイアはプラトン学の牙城として、アリストテレス※の創ったリュケイオン学園はアリストテレス哲学の牙城として、「ギリシアの古典」を守り続けていました。ヘレニズム期にはヘレニズム王国の王族の子弟たちが、ローマ時代にはローマの貴族の子弟たちが、ギリシアの古典文化を学びにアテナイに留学していました。ローマ人は地中海に進出する以前からギリシア文明を尊敬し、学んできましたが、地中海世界を支配下に入れた後も変わりませんでした。しかし、ローマ人が尊敬し学ぼうとしたのは「旧いギリシア」だけのようです。ローマ人は「新しいギリシア」とくに「数学」には興味がなかったようです。
古典期のアテナイの多様性と自由な発想
古典期のアテナイは、発展途上の若々しさがあり、因習にとらわれない大胆で自由な発想がギリシア文明の独創性と独自性を生み出してきました。誰でもが裁判官であり、政治家であり、軍人であり、哲学者であり、数学者でした。討論や対話はその場限りの白熱した真剣勝負でした。しかし「旧いギリシア」となった今、学問は専門の偉い学者の占有物となってしまい、ギリシア哲学の権威と伝統の灯を守ることに汲々としていたのです。一方、「新しいギリシア」では、オリエント文明と混合し、ギリシア語を共通語とした新しい文化を創り出し始めます。特にアレクサンドリアでは、多くの国々からいろいろな分野の人が集まる学際都市となり、科学者たちは未知の領域を切り開き独創的な成果を生みだしていました。
結局西ヨーロッパには数学は伝わらなかったようです。古代ローマの雄弁キケロもローマ人が数学に興味を持っていないことを認め次のように言っています。

ギリシア人は幾何学に最高の敬意を払い、数学者ほど尊敬されるものはいなかった。われわれローマ人は、この技法を測量や計算という実用的なものだけに限定してしまった
しかしキケロ自身もギリシアの哲学や弁証法を学んでいますから、「旧いギリシア」は伝わったようです。ヨーロッパの歴史では、ギリシアの後はローマが続きますが、数学の歴史ではギリシアの後にはローマが続きません。ヨーロッパの人たちから見れば、アカデメイアが閉鎖された529年頃がギリシア文明の終焉に見えるかもしれませんが、これは「旧いギリシア」が消滅しただけで、「新しいギリシア」は東ローマ帝国のもとで、エジプトやシリアやアナトリアで存続し、やがてアラビアで興ったイスラームの人々に受け継がれます。ここで発展した数学をアラビア数学といいます。
ギリシアの没落とエジプトの変遷:ローマ時代の科学と文化
エジプトがローマの属州になると、それまで支配階級にあったギリシア人たちは没落します。しかし、それまで大きな成果をあげてきた科学研究所ムセイオンは存続します。それどころか、ローマ帝国の手厚い保護を受けています。たとえば、紀元130年にローマ皇帝ハドリアヌスは、ムセイオンを訪れ学者たちと懇談していますし、学術振興には出費を惜しみませんでした。数学の研究は一人ではできず、やはり学園とか研究所のような公共の施設が必要のようです。アルキメデス はシチリア島のシラクサで一人研究を続けましたが、常にアレクサンドリアの学者たちと手紙のやり取りをしています。ローマは、科学研究はアレクサンドリアにまかせ、本国のイタリアには科学研究機関は作らなかったようです。
しかしアレクサンドリアにおけるギリシア人の零落はだんだん目立つようになってきます。それに代わってエジプト系ローマ人が政府の要職に就くことが多くなります。このころはギリシア人もかなり混血していたようですし、学者たちのなかにもエジプト人や外国人が増えてきます。たぶんそのためでしょう、ギリシア人の中にバルバロイ(蛮人)に対する差別意識が強くなってきたようです。またローマの著述家、たとえばストラボン、ディオドロス、プリニウス、プルタルコス※などは、ギリシア文化を崇拝するあまり、ギリシアのことをあまりよく書かなかった歴史家ヘロドトス※をひどく嫌って酷評するようになりますし、エジプト文明に対しても、野蛮で原始的だと見るようになっています。ヘロドトスの評価は、このように時代によって乱高下します。
--Advertising--
古代ローマの建築家ウィトルウィウスと実用数学
上でギリシアの数学はローマには伝わらなかったと述べました。以下この節では、次のチャプターにも登場するローマ人の有名な建築家で数学者のウィトルウィウスについて見てみましょう。
ウィトルウィウスは、プトレマイオス王朝の終焉の頃からエジプトがローマに併合され地中海アジアの大部分がローマの領土となる頃に活躍しました。当時ローマでは巨大な石造建築、大浴場や柱廊付の建物や庭園、それに遠方から水を流す水道の建設が盛んに行なわれるようになりました。それを指揮したのがウィトルウィウスです。ウィトルウィウスが著した全10巻の『建築について』という著作は、その後長い間千年以上も、後のルネサンス期の建築設計者に至るまで大きな影響を与えました。ウィトルウィウスはギリシアの理論数学をある程度理解していたかもしれませんが、むしろオリエントの実用数学を好んで用いていたようです。
たとえばウィトルウィウスが用いた π の近似値は、アルキメデスの見つけた22 7 ではなく25 8 でした。なぜ 22 7 を使わなかったのでしょう。アルキメデスの著作は難しすぎてあまり読まれていなかったという意見もありますし、当時のオリエントでは25 8 が使われていたためかもしれません(バビロニア数学では 25 8 でした)。
ここでエジプト数学について少し解説しておきます。エジプト数学では四則演算は2倍法と2分法を基本としていました。2倍法は2倍、2倍していく方法で、2分法は、半分、半分、と半分に割っていく方法です。すると、a 8 は a を半分に割り、半分に割り、さらに半分に割ることで計算できます。また、1 7 と 1 8 の差は
1 7 ー 1 8 = 1 56
にすぎません。ウィトルウィウスはエジプト式で計算していたと思います。前節で述べた円周率の計算の中で、アルキメデスは 1 7 の代わりに 1 8 を用いています。中世ヨーロッパにおける算術の掛け算や割り算は2倍法と2分法を使っていますが、これもエジプトから伝わったのかもしれません。
しかしこれはウィトルウィウスが正確さを軽視していたわけでは決してありません。彼は水道の設計についての著作の中で、水を滞りなく流すにはその勾配を 1 : 4,800 にするのがよいと述べています。これは 4.8km いくごとにたった 1m しか下がりません。実際古代ローマの有名なポン•デュ•ガールの巨大な3段アーチの水道では、最上段の全長 275m もの長さに対して、高度差はたった 2.5cm でしかありません。
関連記事以下の記事で詳しく解説しています++。
ウィトルウィウスの『正方形が2つ並んだ形の作図』
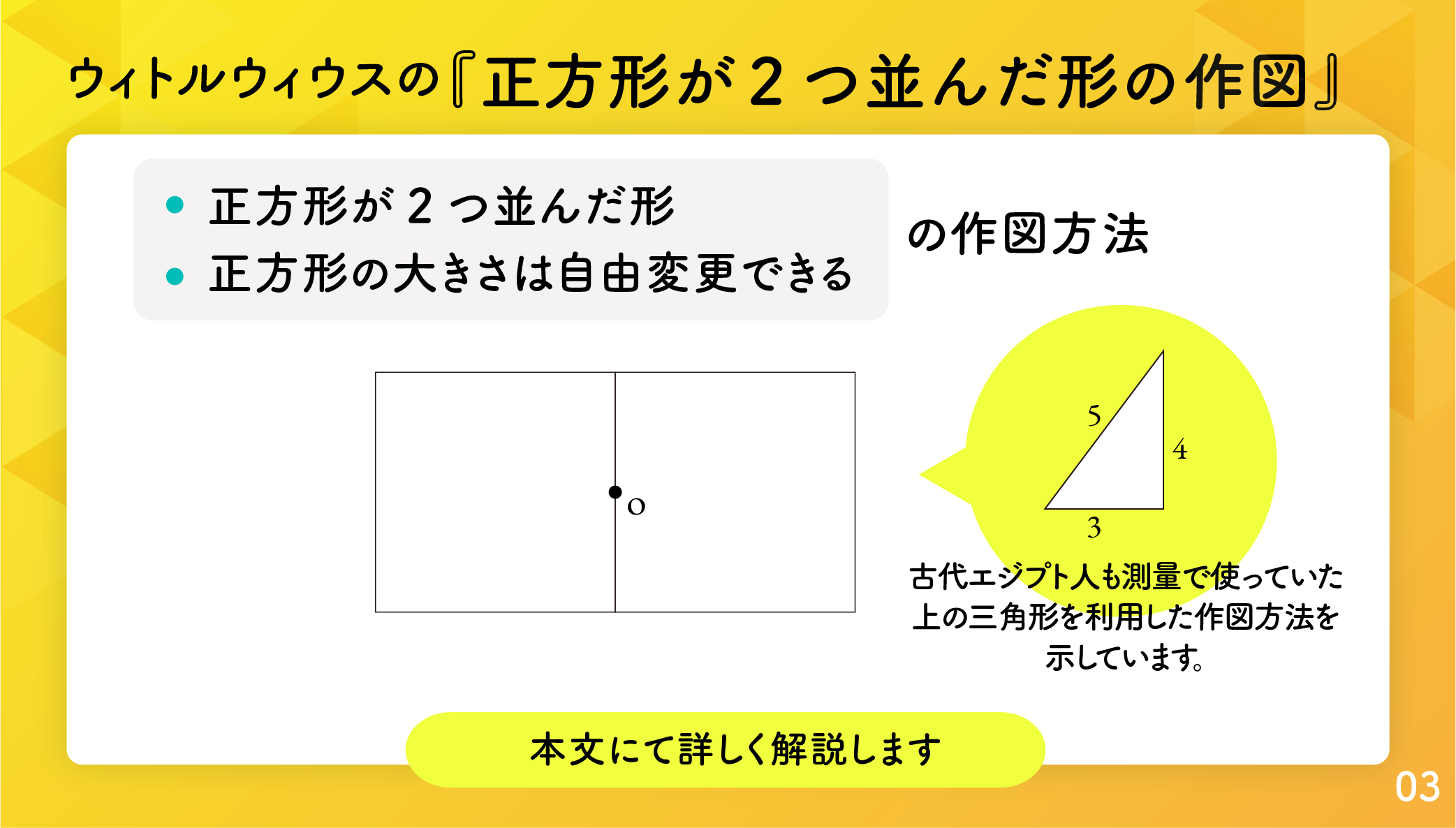
さてウィトルウィウスは、正方形が2つ並んだ形、あるいは3つ並んだ形の作図法について述べています。正方形が2つ並んだ形から始めましょう。祭壇かなにかの設計で、中心 O が与えられたとき図4.6.1 のように正方形を2つ並べます。このとき2つの正方形を自由に大きくしたり小さくしたりできるようにしたいのです。
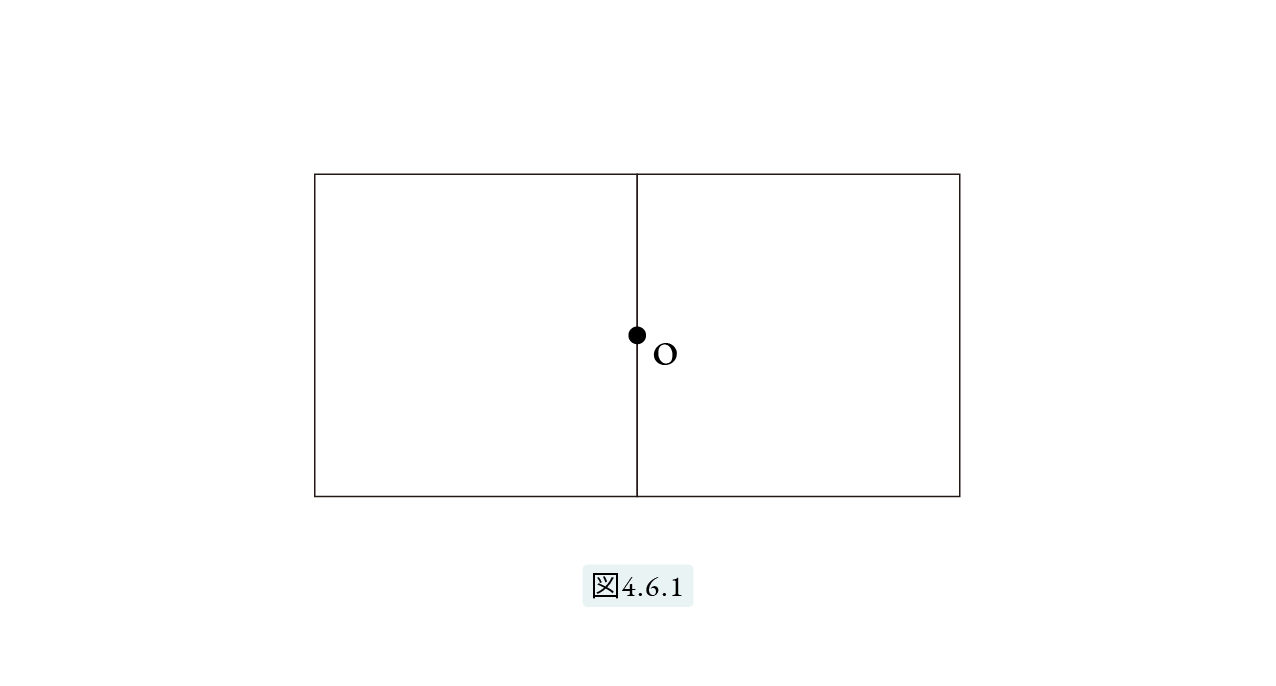
以下では、ウィトルウィウスがこの作図をどのように示したかを説明します。まずは動画で作図方法をみてみましょう。
上の動画で説明した作図方法を文章でもおさらいしておきます。3-4-5の直角三角形 XOY を図4.6.2 のように置きます。
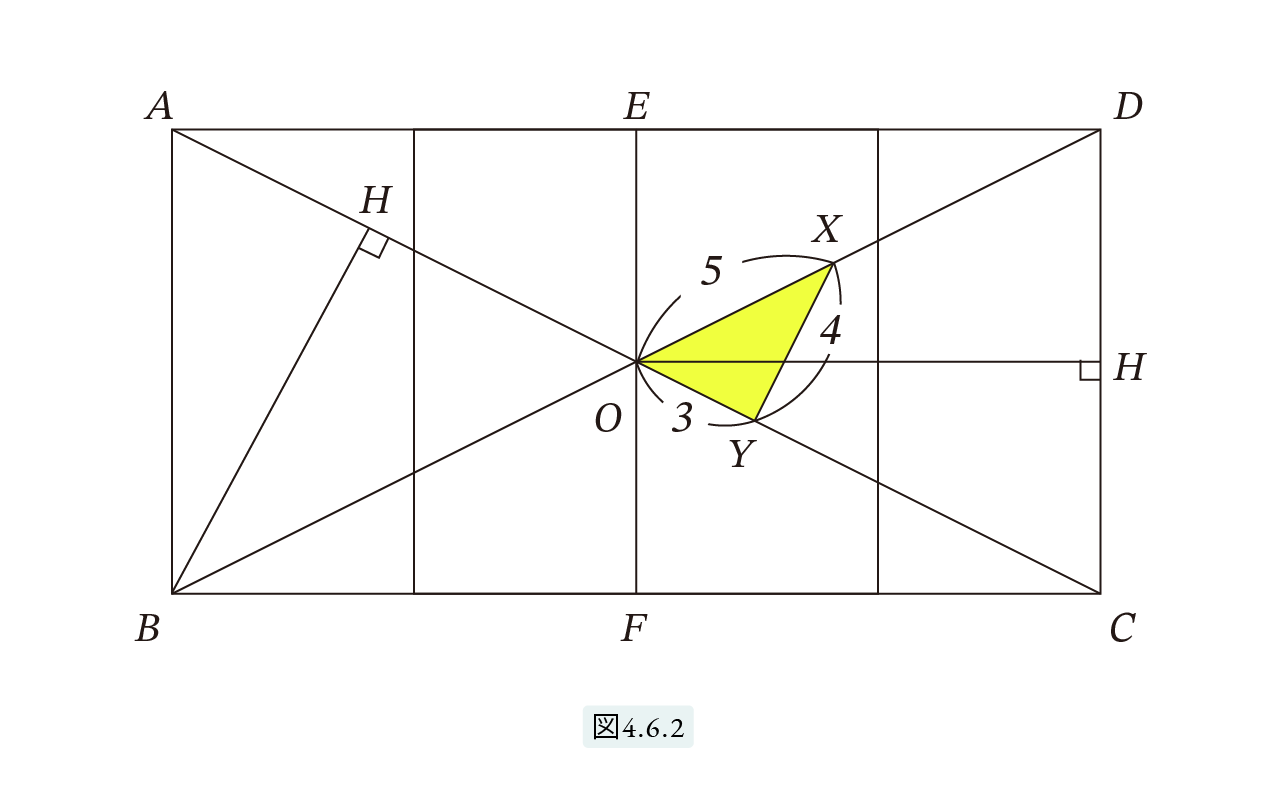
OX=5, OY=3, XY=4 とします。OX と OY を両方向に延長します。この2つの直線上に点 A, B, C, D を AO=BO=CO=DO となるように取ります。すると、以下で示すように ABCD は正方形が2つ並んだ形になります。AO の長さは適当に決めることができますから、正方形の大きさは自由に決めることができます。つまりこれは「点Oが与えられたとき、O が中心にくるように正方形が2つ並んだ祭壇を設計する方法」なのです。
では、続いて上の作図方法で、ABCD は正方形が2つ並んだ形であることを証明しましょう。
証明
Fを BC の中点、 Eを AD の中点とすると、三角形OBC は2等辺三角形だから ∠F は直角になります。ABFE が正方形となることを証明します。OAの長さは任意に決めたのですから、OA=5 としてかまいません。
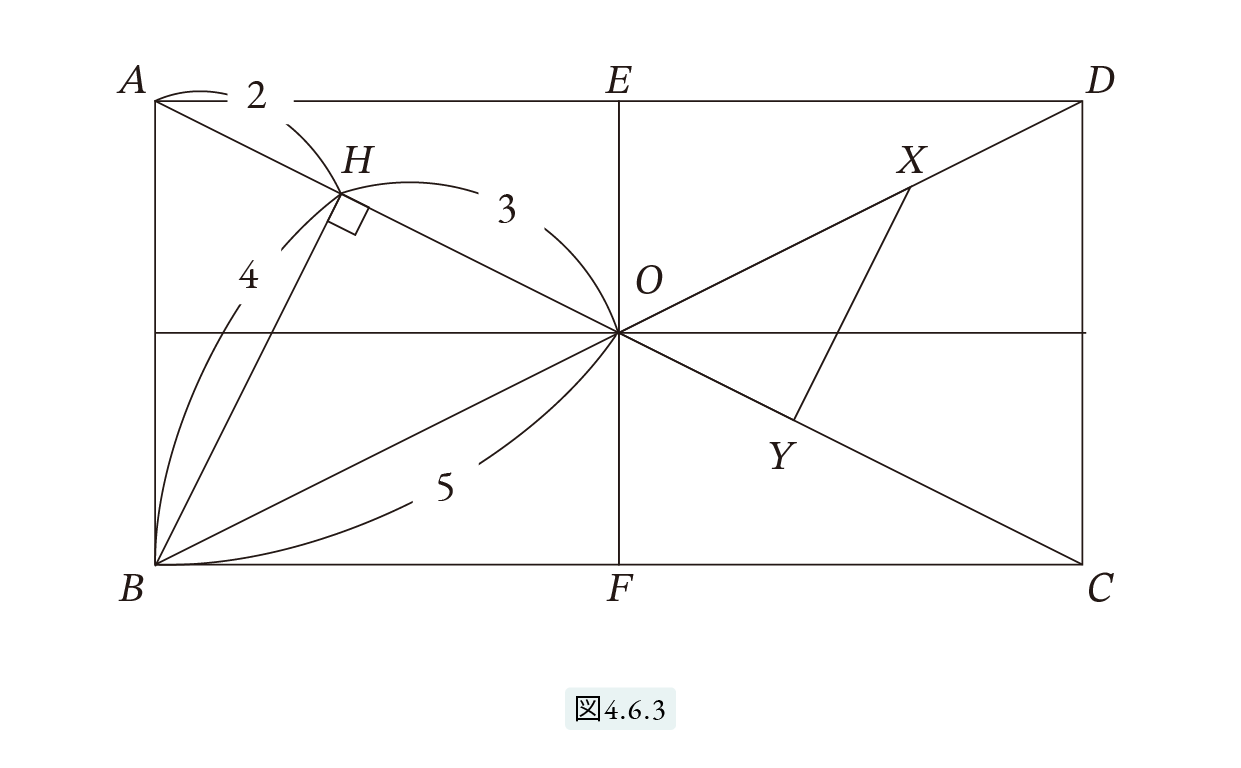
点B からOA に垂線 BH を下ろします。すると △XOY と △BOHは相似となります。OB=5 ですから、 OH=3, BH=4 となり AH=2 となります。また CO=OA, CF=FB より OF と AB は平行です。図4.6.3 で示されるように、∠FOB = ∠OBA = ∠BAH ですから、直角三角形AHB とOFB は相似です。
よって
OF : BF = AH : HB = 2 : 4 = 1 : 2
となります。 OF は BF の半分で、OF は AB の半分でもありますから AB = BF となります。
この証明では三角形の相似を使っていますが、相似比は整数です。ギリシアの幾何学では数値が出てきません。したがって、3 – 4 – 5 の直角三角形などは現れてきません。また、ギリシア数学では、こういった「祭壇の設計」などの応用は「レベルの低い職人の数学」とみなし扱いませんでした。つまり、ここでの数学はギリシア数学ではなくエジプト数学なのです。
ウィトルウィルスがなぜこんな面倒な作図法を述べているのかは謎です。長さを測ったり直角を作る器具を使わず、縄だけで作図したかったのでしょうか。あるいは幾何学を教えたかったのかもしれません。
ウィトルウィウスの『正方形が3つ並んだ形の作図』
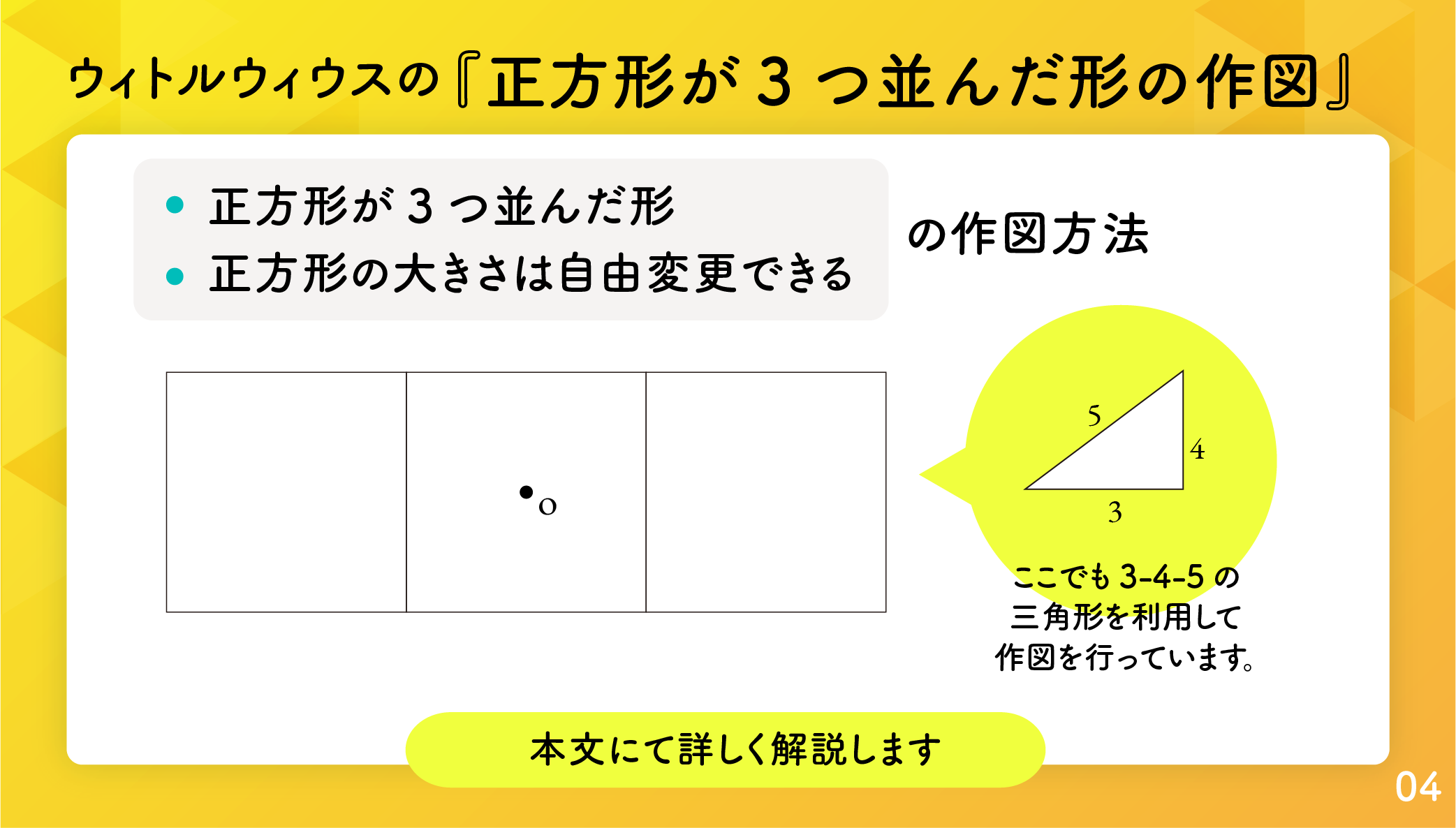
今度は『正方形が3つ並んだ形の作図』を考えます。作図方法は『正方形が2つ並んだ形の作図』とほぼ同じで OX=5, OY=4 とするところだけが異なります。
証明
BからOAに垂線 BH を下ろし、OからBC に垂線 F を下ろします。OB=5 としてもかまいません。すると、OH=4, BH=3, AH=1 となります。図4.6.4 参照。
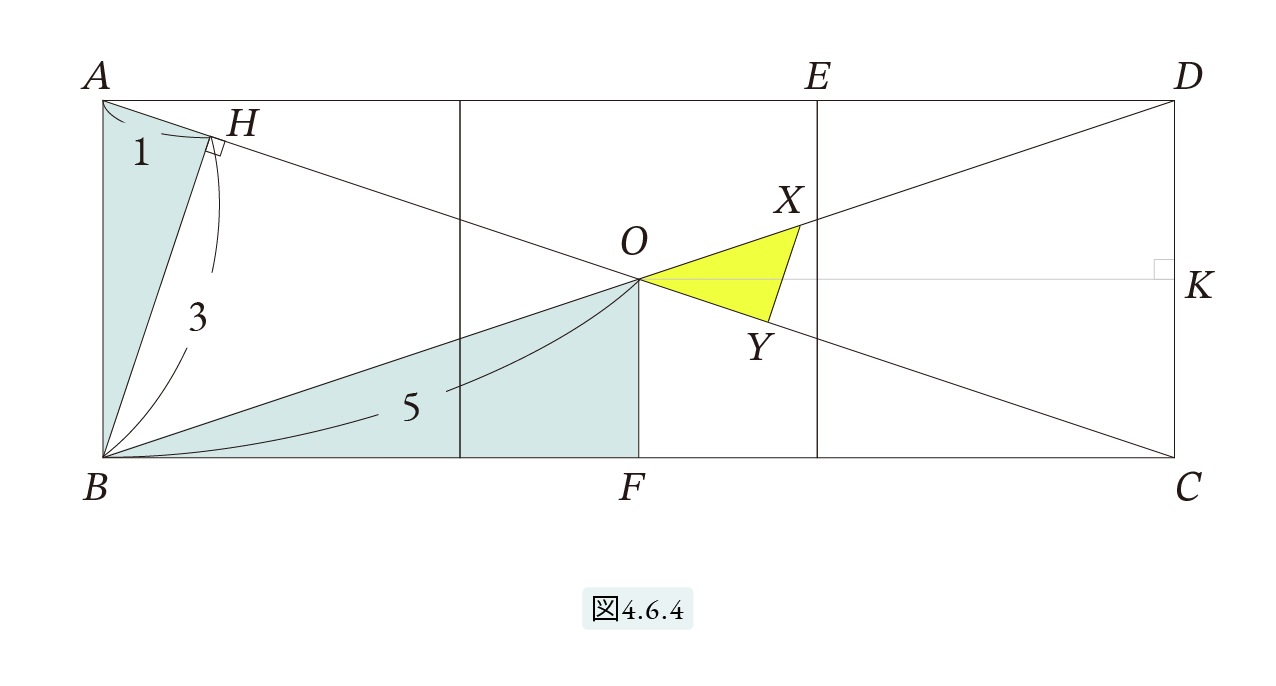
前と同様 △AHB と △OFB は相似となります。よって
OF : BF = AH : HB = 1 : 3
となります。したがって AB : BC も 1 : 3 となり、長方形 ABCD は正方形を3つ並べた形となります。
3 – 4 – 5 の直角三角形はこのようにとんでもないところに出現します。とても不思議な感じがしませんか。
ウィトルウィウスと黄金三角形
ウィトルウィウスは上の『正方形が3つ並んだ形』の中にある三角形 OCD が黄金三角形となっていると主張しています。黄金三角形とは五芒星※にあらわれる三角形のことで、図4.6.5の三角形 ABC のことです。KはDCの中点です。
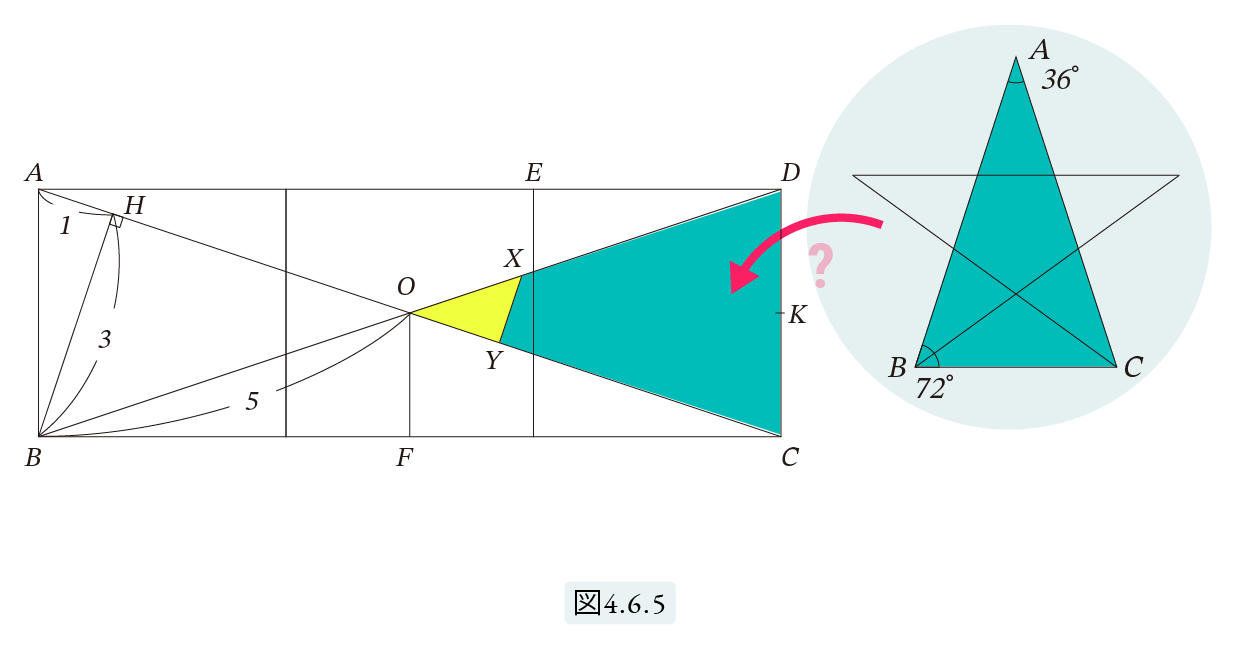
この主張がどれほど厳密に正しいかを計算して調べてみましょう。2つの角度 ∠COD と ∠OCD を tan-1 を使って計算してみましょう。
∠COD = ∠YOX = tan-13 4 = 36.87
∠OCD = ∠OCK = tan-13 1 = 71.565
五芒星にあらわれる三角形の角度はそれぞれ36°と72°なので正確には異なります。三角形OCD は見た目には黄金三角形とほとんど同じに見えますが、“全く同一”とはならいようです。
また、ウィトルウィウスは三角形OCD を使うと円を10等分できると言っていますが、36.87 を10倍すると368.7 となり、9度近く違っています。ウィトルウィルスは、古代ローマの当代随一の数学者として扱われています。しかし使われている数学はきわめて初等的です。
続いてOC : CD が黄金比となっているかも試してみましょう。
OC CD = 5 = 2 =1.5811⋯ ≒ 1.6
ほぼ黄金率となっていますが正確には違います。ギリシアの理論数学なら厳密な証明を与えるところです。
古代の数学者に対し少し厳しすぎる意見のように思えますが、これは後で黄金率の議論でウィトルウィルスが出てくるからです。
--Advertising--
まとめ
ウィトルウィウスの議論のなかに 3 – 4 – 5 の直角三角形が現れていることに注意してください。これは、縄師とよばれるエジプトの測量士が直角を作るのに用いたといわれている三角形です。ウィトルウィウスはこの 3 – 4 – 5 の直角三角形と黄金比を関連付けていることにも注意してください。ウィトルウィウスの議論のしかたは、ギリシアの理論数学より、エジプトの実用数学を思わせます。証明はまったく出てきません。水道橋の設計の場合は非常に正確な数値計算をしますが、円周の長さに関しては、わりと大雑把な計算をしています。ウィトルウィルスの実用数学にとってこれで十分だったと思われます。また、ウィトルウィルスは黄金比(外中比)などの用語は使っていません。厳密な定義などは考えず、「五芒星の主要な部分となる三角形」とぐらいに思っていたのでしょう。ウィトルウィルスにとって五芒星も、正確な正五角形になる必要はなく、左右対称で美しければそれでよかったのかもしれません。