ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
4-2.ピタゴラスの定理:古代ギリシアにおける数の扱い
ページ目次
古代ギリシア数学の概念とピタゴラスの定理
「古代ギリシア人がピタゴラスの定理を証明した」という表現の誤りについて
この節ではギリシア人が数をどのように捉えていたかを考えます。もう少し正確に言うと、ユークリッド※の『原論』において、長さとか面積とか体積がどのように扱われていたか、についてです。私たちはどうしても過去の数学を現代人の眼で見てしまいます。たとえばピタゴラスの定理は、通常次のようにいわれています。
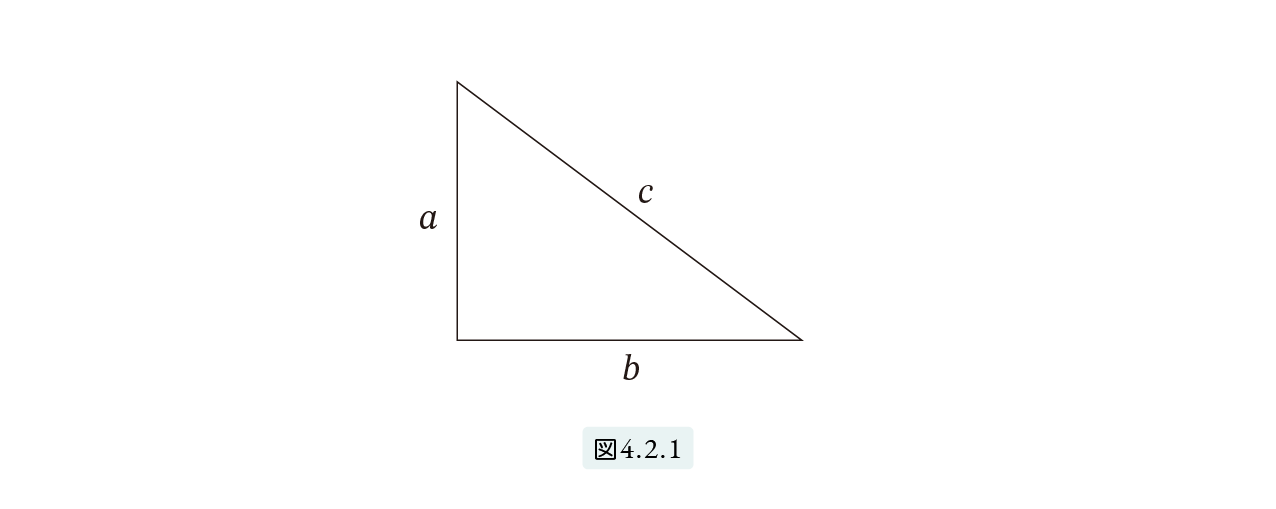
定理 A 図4.2.1 の直角三角形において次が成立する。
c2 = a2+ b2 (1)
また、ギリシア人が発見した定理として次も有名です。
定理 B は無理数である。
しかしながら数学史の表現としては、「ギリシア人は定理 A を証明した」とか、「ギリシア人は定理 B を証明した」という言明は、実は間違いなのです。この節では、この表現のどこが間違っているのかを説明します。
--Advertising--
古代ギリシア人の数の概念:数と量
現代の私たちは、長さ、面積、体積、角度などを数で表していますから、古代ギリシア人も私たちと同様だと思いがちですが、実はそうではありません。ギリシア人にとって数とは個数を表わす自然数だけだったのです。ここでいう古代ギリシア人とは、文芸や哲学で名高いギリシア文明が花開いた古典期の都市アテナイの人々、特に幾何学という数学の原点を創設した人々のことです。科学の中心が都市アテナイから、エジプトのアレクサンドリアに移ると、エジプトやバビロニアの実用数学の影響を受け、数学も大きく変貌します。ギリシア人も1よりも小さいエジプト分数やバビロニアの 60進小数を使うようになり、数の概念も変わってきます。エジプト人やバビロニア人は面積や体積を
面積=長さ×長さ
体積=長さ×長さ×長さ
として扱っていました。しかし、アルキメデス※などギリシアの理論数学を順守する人たちはこの立場を取っていません。ギリシアの「幾何学」の流れの中で理論を展開しています。
長さ、面積、体積、角度など自然数以外の数を量と呼びます。あるいは現代の物理でよく使われる、
3メートル、3平方メートル、3立方メートル、3度
のような「単位名つきの数」だと考えた方が理解しやすいかもしれません。また、以下では混乱を避けるために、数の代わりに自然数という用語を用いることにします。
古代ギリシア人が作り上げた幾何学
ピタゴラスの定理
なぜギリシア人が数と量を峻別したかはあとで議論することにして、このような枠組みでギリシア人がどのようにして歴史的偉業である「幾何学」を作り上げたか見てみましょう。ここではその代表的な例として「ピタゴラスの定理」をとりあげます。
「幾何学」では4つの量、長さ、面積、体積、角度、を扱いますが、これらはそれぞれ独立した別種のものです。演算は足し算と引き算だけですが、許されるのは同じ種類の量に限ります。たとえば次は許されません。
長さ+面積、長さ+体積、長さ+角度、…
同じ種類の足し算が許されますから、自然数倍も許されます。a を量、n を自然数とするとき、na は次で定義されます。
na = a + a + … + a (n個)
上の定理 A で、a2 は a × a という意味です。しかし、量には掛け算が定義されていません。ギリシアの幾何学には「長さ×長さ」という概念はないのです。例えば、
定理 A 図4.2.1 の直角三角形において次が成立する。
c2 = a2+ b2 (1)

3メートル + 4メートル = 7メートル は〇
3メートル × 4メートル = 12平方メートル は×
となります。
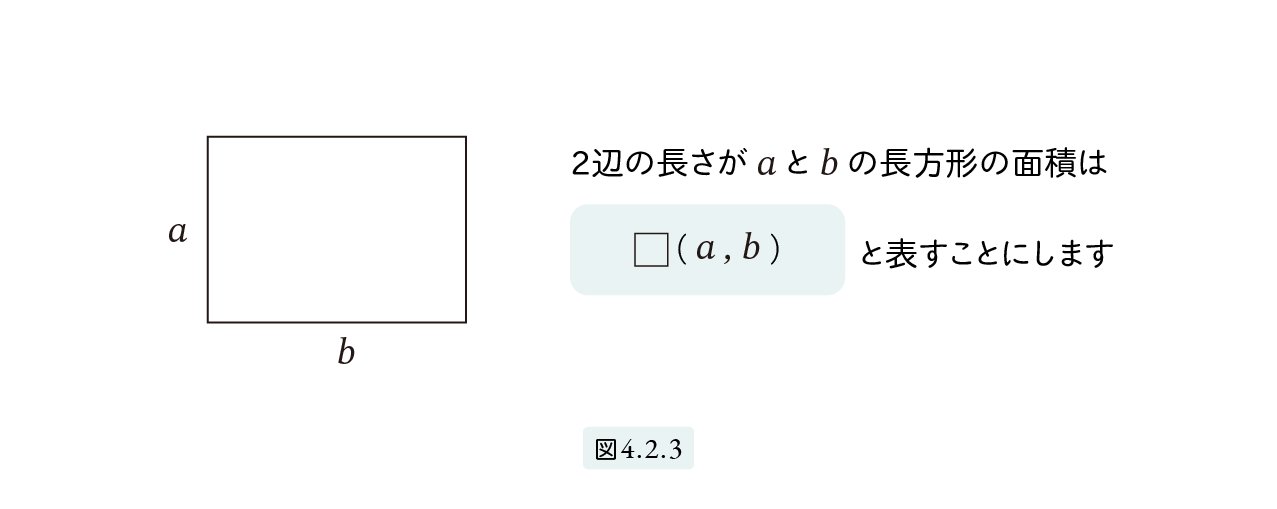
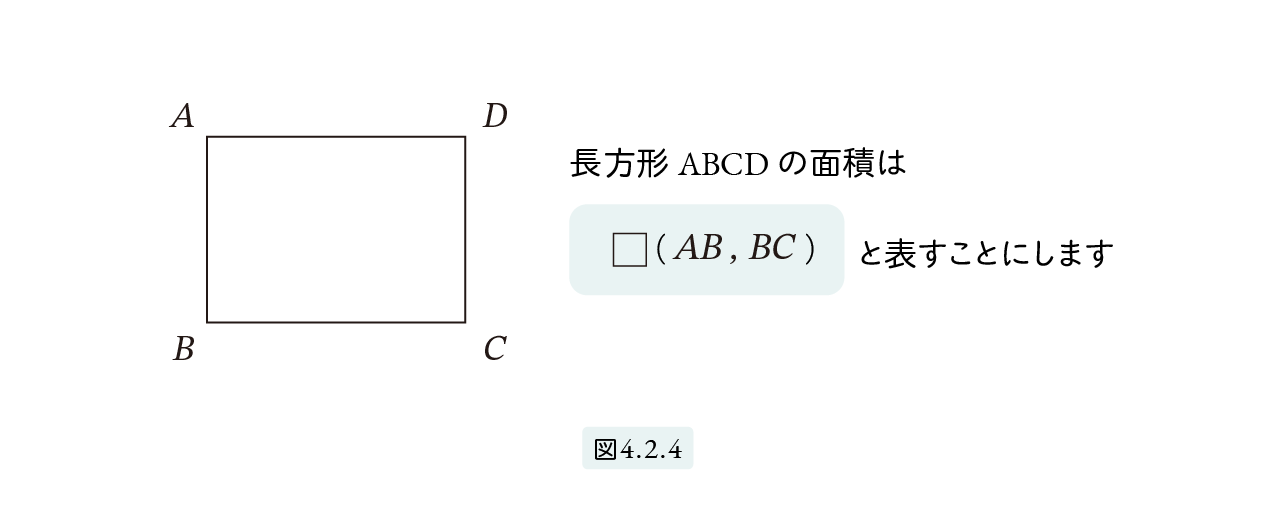
面積は長さとは独立した量として扱われます。図4.2.3のように、2辺の長さが a と b の長方形の面積を □( a , b ) で、図4.2.4 の長方形 ABCD の面積を □( AB, BC ) で表すことにします。また、1辺が a の正方形の面積を □2(a) で表すことにします。ここで、□2(a) は □(a.a) の略記法であって、2乗を意味するものではないことに注意してください。
ピタゴラスの定理を、ギリシアの概念だけを使って述べなおすと次のようになります。
定理 4.2.1 (ピタゴラスの定理)
図4.2.1の直角三角形において、次が成立する。
□2 ( a ) + □2 ( b ) = □2 (c) (2)

この表現も式を使っているので、古代に忠実だとは言えません。式 (2) は次のような言葉に翻訳できます。
直角三角形において、斜辺上の正方形は、
直角をはさむ2辺上の正方形の和に等しい
式 (1) と式 (2) は本質的に意味が違うことに注意してください。式 (1) の a2 は実数 a の2乗を表し、式(2) の □2(a) は1辺の長さが a の正方形の面積を表しています。
平行四辺形の面積と合同
古代の数学について述べるときには、用語については細心の注意が必要です。数学史の専門家はこの点に非常に苦労されています。この点において本連載はあまり厳密ではありません。現代の読者になるべくわかりやすく現代風に言い換えています。『原論』では 長さ、面積、体積という用語は用いていません。これらは、それぞれ、線、領域、立体の大きさと表現されます。例えば、「線分 AB と線分 CD が同じ大きさ」である、とは「ABの長さとCD の長さが等しい」ことです。
同じ種類の量に関しては、大きさの大小が定まることがあります。「図形 a が図形 b の一部」であるとき、「図形 a は図形 b より小さい」といいます。 本連載では等号 = は「同じ大きさ」を表します。例えば「△ABC = △DEF」は、「三角形ABC の面積は、三角形DEF の面積に等しい」の略記法です。
幾何学には、同じ量 という関係のほかに合同という重要な概念があります。ある図形 a が、移動したりひっくり返したりして図形 b とピッタリと重なるとき、図形a は図形 b と合同であるといいます。もちろん、合同なら同じ量です。
面積に関する議論で基本となるのは三角形ですが、まず平行四辺形について考えます。図4.2.5 のような底辺 AB を共通とし、上辺 DC と EF が同一直線上にある2つの平行四辺形ABDC と ABFE を考えます。
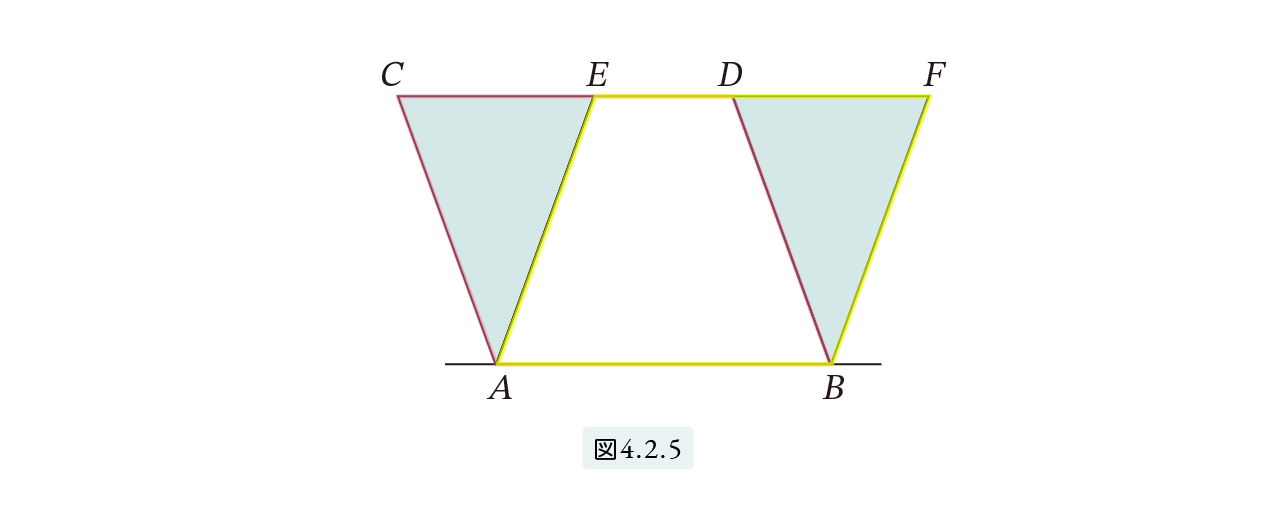
次の定理はこの2つの平行四辺形の面積が等しいことを言っています。
定理 4.2.2 底辺と高さが等しい2つの平行四辺形の面積は等しい。
図4.2.5 で、CD = AB = EF です。したがって
CE = CD – ED = EF – ED = DF
さらに平行四辺形の性質より CA=DB, EA=FB です。よって三角形CAE と三角形DBF は合同、つまり等しいことになります。よって、
平行四辺形ABDC = 三角形CAE + 台形 EABD
= 三角形DBF +台形 EABD = 平行四辺形 ABFE
となり、定理が証明されました。
三角形の面積
定理 4.2.3 底辺と高さが等しい2つの三角形の面積は等しい。
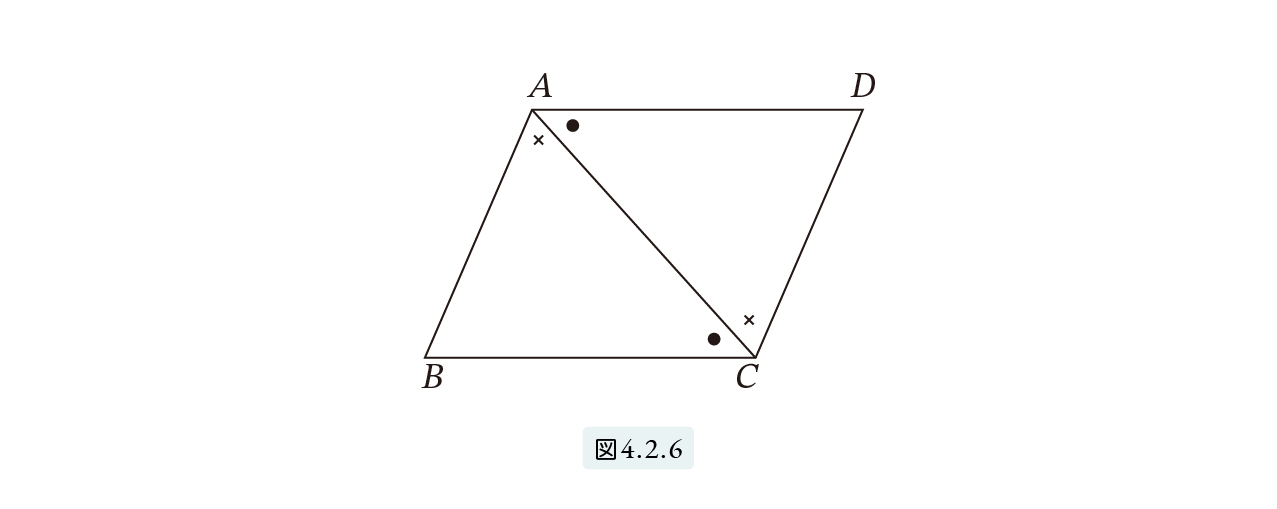
任意の三角形 ABC は、図 4.2.6 のように合同な三角形 CAD を張り合わせると、平行四辺形 ABCD となります。三角形は平行四辺形の半分ですから、定理 4.2.3は定理 4.2.2 からただちに得られます。
PICK UP!!こちらのWeb連載もおすすめです

--Advertising--
ピタゴラスの定理の証明
それでは定理 4.2.1(ピタゴラスの定理) の証明をしましょう。ピタゴラスの定理はとても数多くの証明があることで有名ですが、次は『原論』にある証明で、とても美しいことで有名です。図4.2.7 をみてください。
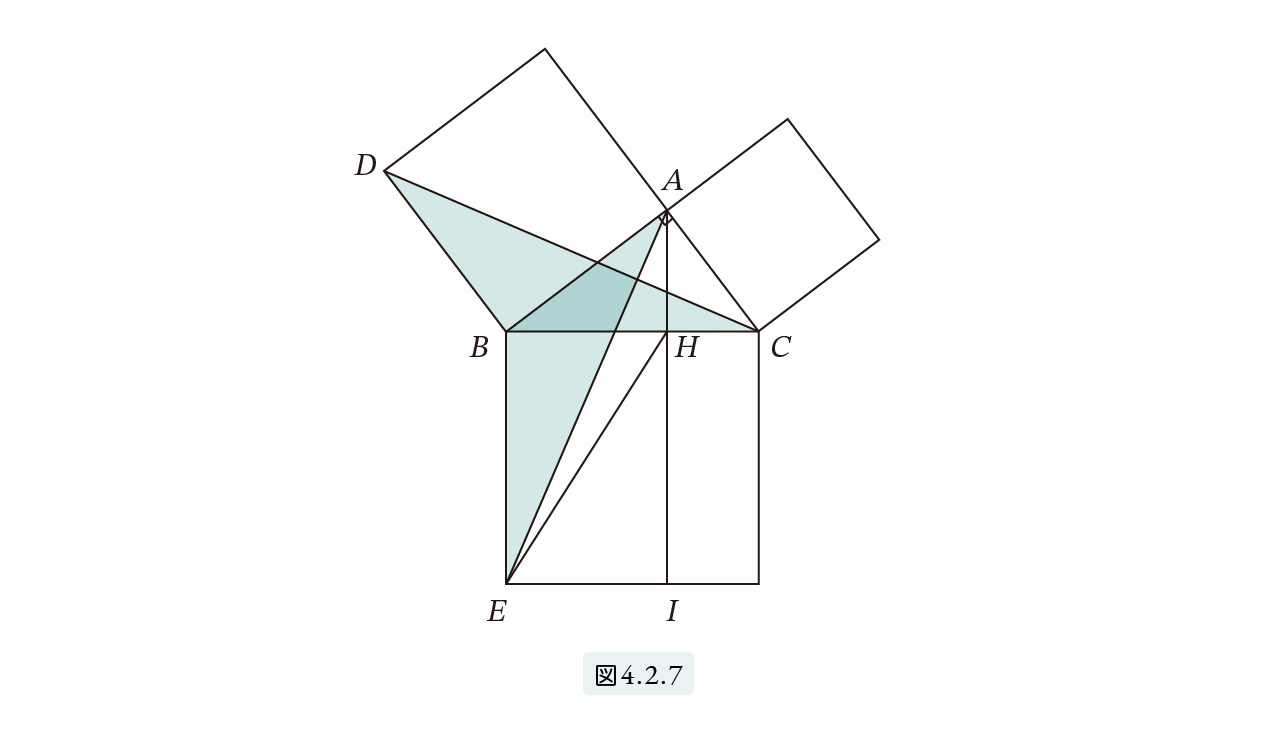
三角形 DBC と三角形 ABE は2辺夾角で合同です。また、今証明した定理4.2.3 より
三角形 ADB = 三角形 DBC, 三角形 ABE = 三角形 HBE
となります。これらを合わせると、
三角形 ADB = 三角形 DBC = 三角形 ABE = 三角形 HBE
よって、
□2(AB) = 2×三角形 ADB = 2×三角形 HBE = □(BH, HI)
同様にして □2(AC) = □(HC, HI) が証明できます。これより
□2(AB)+□2(AC) = □(BH, HI)+□(HC, HI) = □2(BC)
が得られます。
▼動画説明でこの証明をおさらいしてみましょう。
無理数と共測
次に定理 B を考えます。
定理 B は無理数である。 (再録)
まず数学の復習をしましょう。私たちは という記号で、「2乗すると2となる正の実数」を表しますが、ギリシア人はこんな便利な記号を持っていませんし、長さに数値を結びつけることもできませんでした。したがって、無理数とか有理数という概念もありません。復習すると、有理数とは、分母と分子がともに整数の分数で表せる数のことで、無理数とは有理数ではない実数のことです。
ギリシア数学では、長さなどの量は数値に結びつけるのではなく、比に結びつけました。つまり、数という概念の代わりに共測という概念を用いたのです。たとえば2本のロープ A と B があったとしましょう。A と B の長さを評価するために、基準となるロープ e を使います。A は e が 3 個分、B は e が 7 個分であったとします。すると A と B の長さの比は 3 : 7 となります。もし A か B のどちらかが e で正確に測れないなら、さらに小さな単位のロープを用います。もし、A と B が共通の単位で測れるなら、A と B は共測であるといいます。共測という用語は通約可能と呼ばれることもあるので覚えておいてください。
一般の量に対し共測という概念を定義しておきます。与えられた量 a と b に対し、ある量 e と自然数 m と n が存在し、a = me, b = ne と表されるとき、a と b は共測であると言います。簡単にいうと、「2つの量 a と b が共測であるとは、a : b が自然数の比 m : n で表わせること」となります。定理 B はギリシアの幾何学では、次のように表現されなければなりません。
定理 4.2.4 正方形において、一辺の長さと対角線の長さは共測でない
この定理の証明は省略します。本によっては、無理数の代わりに無理量としているものもありますが、このような量も『原論』には出てきません。またよくある間違いは、自然数を(特別な)量と考えていることです。これは、自然数が(特別な)実数であることからの類推だと思われます。
--Advertising--
古代ギリシア人はなぜ自然数と量をきりわけたのか
ではなぜギリシア人は数(=自然数)と量とを切り分けたのでしょうか。よく言われている理由のひとつは、定義の難しさです。長さとか面積をどのように定義したらよいのか? 現在のように「量=実数」とみなすと、実数の定義が必要となります。こういったものはやっと19世紀になってから考えられるようになったものです。ギリシア人ができなくて当然です。しかしこれは少しギリシア数学を買いかぶりすぎかもしれません。理由はもっと単純なものかもしれません。
理由の一つは記数法です。私たちは言葉を使って考えます。したがって言葉によって思考が制限されます。ギリシア人の記数法は、ローマ数字と同様のもので極めて原始的なものでした。また、自然数と比べ、長さや重さや容量(体積)などは、単位が10 進ではなく複雑でした。したがって、量を抽象的な数に結びつけるのがなかなか難しかったのではないかと思います。
もう一つの大きな障害は、量に対して絶対的普遍的な単位を想定できなかったためです。現在の私たちは、長さに対しては1メートルという単位を、重さについては1グラムという絶対的な単位を持っていて、世界中どこに行っても同じです。しかしギリシア世界はまだ国としてまとまっておらず、多くのポリスの集合体で、ポリスごとに長さや重さの単位度量衡が違っていたのです。つまり、「量というものは常に相対的なもの」だったのです。
それともうひとつの大きな理由は、ギリシア数学が理論数学であって、実用数学ではなかったこともあると思います。数という概念を習得するには毎日のように数を扱って、実際に計算を繰り返しやってみる実践が必要だと思います。そのことによって数というものを、あたかも実在するもののように感じることができるのです。しかしときには実用を忘れ、純粋に思索に耽ることも必要です。そうでなかったなら、定理4.2.4 のような定理を思いつくことはなかったでしょう。また、現在の数学の原点ともなるギリシア数学も生まれなかったと思われます。
