ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
5-3.ピラミッドの『黄金比の謎』を解明する
ページ目次
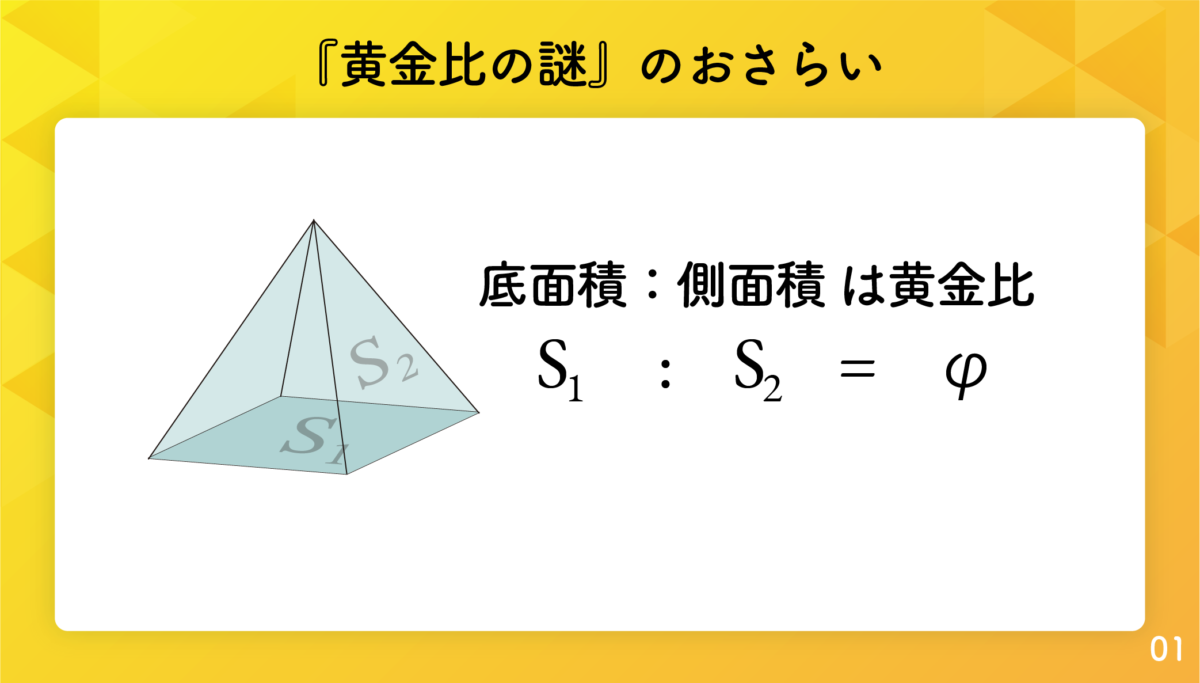
ピラミッドの『黄金比の謎』のおさらい
この節では、なぜピラミッドに黄金比が現れるのか、について考えてみたいと思います。また、ピラミッドのセケドが 5;1 2 から 5;1 4 に変わった理由についても考えます。数学は、ピタゴラスの定理と平方根の計算が出てきますが、論理はそれほど難しくはないと思います。関数電卓を使って実際に計算してみてください。
前にも述べましたが、黄金比という用語は近世につくられたもので、古典期のギリシアでは外中比と呼んでいました。しかし本連載では皆さんがよく知っている黄金比、黄金率という用語を用いることにします。
まず復習をしましょう。a と b を a < b を満たす正の実数とします。次を満たすとき、a : b は黄金比であるといいます。
a : b = b : a + b (1)
小さい方 : 大きい方 = 大きい方 : 全体
a : b が黄金比であるとき、b a を黄金率と呼びます(分母と分子が通常と逆であることに注意してください)。黄金率はよくギリシア文字 φ で表します。『4-3.黄金比とは何か』で述べたように
φ = 1+ 2 = 1.618033989 (2)
となります。
この節では、あるピラミッドが黄金比の謎を満たすとは次が成立することを言います。
黄金比の謎 底面積:側面積は黄金比である。
ここで、底面積も側面積も実際に測定した値ですから測定誤差を持ちます。したがって、黄金率も正確に φ でなくても φ に近い値であればよいとします。まず、エジプト人がどう考えていたかではなく、現代数学を使ってこの問題を考えましょう。円周率の謎と同様、黄金比の謎に対しても次が成立します。
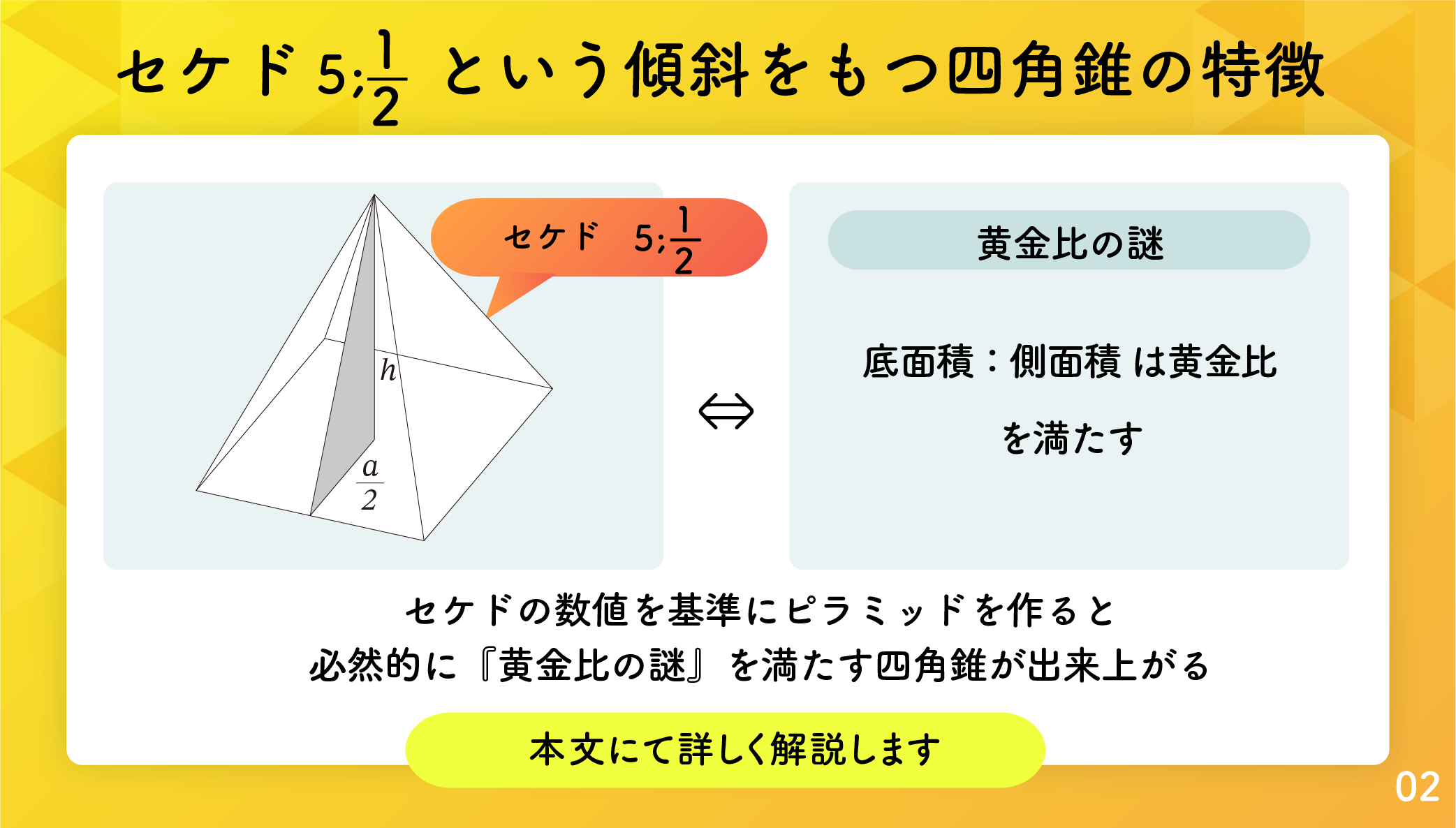
事実2 ピラミッドのセケドは 5;1 2 ⇔ ピラミッドは黄金比の謎を満たす
証明
高さ h、底面の1辺が a のピラミッドを考えます。図5.2.1参照。
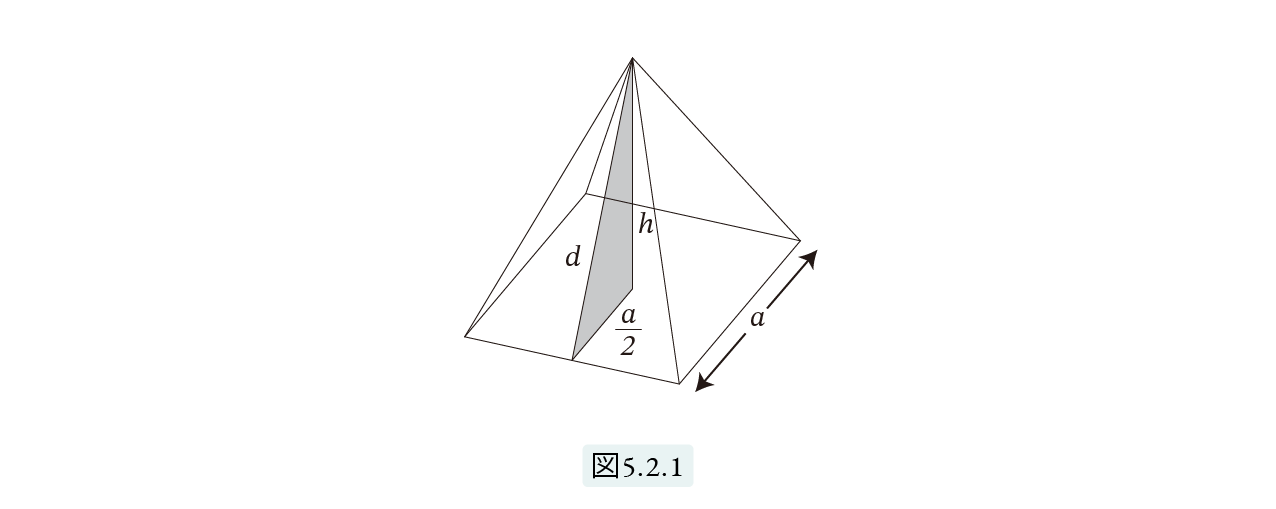
セケドを 5;1 2 とします。すると、傾きは 14 11 ですから
h a/2 = 14 11 よって h = 7 11 a
となります。底面積を S1、側面の4つの三角形の一つの面積を S2 とします。 S1 = a2 です。S2 を求めるために、S2 の高さ d を求めます。ここでピタゴラスの定理を使うと
d2 = (a 2)2+ h2 = a2 4{1 + (2 a)2×(7 11a)2}
となります。
S2 = ad 2 ですから
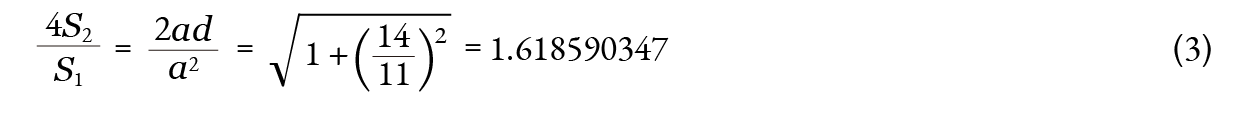
となり、この値は (2) の黄金率の理論値φと驚くべき一致をします。
続いて逆を示しましょう。底面を S1、側面の 1 4 を S2 とし、4S2 S1 = φ とします 。高さを h、底面の1辺を a、S2 の高さをd とします。S1 = a2 ですから、
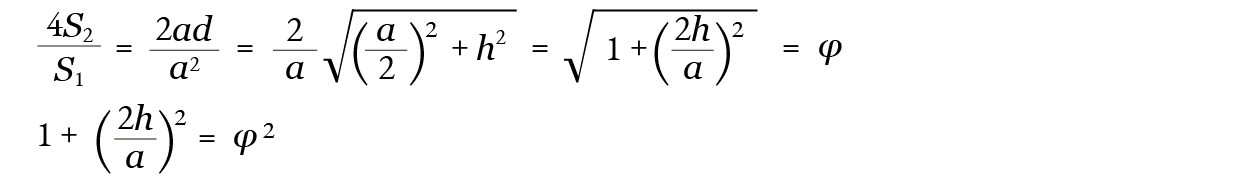
『4-3.黄金比とはなにか』で述べたように 1 + φ = φ2 が成り立ちます。よって、
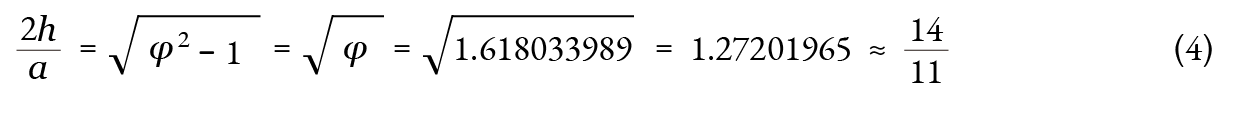
傾き 14 11 はセケド 1 2 = 5;1 2 です。 以上より 事実 2 が成立することが示されました。
関連記事以下の記事で詳しく解説しています++。
数学の世界では『ピラミッドの謎[黄金比]』はどう解釈できるか
『5-1.ピラミッドの『円周率の謎』を解明する(1)』で述べた事実1 と事実2 では、円周率と黄金率は近似値でもよいとしました。すなわち、数学的に正確に一致することまでは要求しませんでした。それでは真の円周率 π と真の黄金率 φ が存在する魔法の世界、つまり数学の世界ではどうなるのでしょうか。「底面積:側面積= 1 : φ」となるピラミッドを黄金ピラミッド、「底面の周長 ÷ 2 × 高さ= π 」となるピラミッドを円周率ピラミッドと呼ぶことにします。このようなピラミッドは数学の世界にしか存在しません。たとえば、ピラミッドの高さをメートルで測るとして、小数点以下無限桁どころか、たった100桁でさえ原子の大きさ(小ささ)をはるかに越えてしまいます。言い換えると、原子の大きさを越える値まで π や φ の値と一致するようなピラミッドが存在するのは数学の世界だけです。
次を証明します。
事実3 黄金ピラミッドは円周率ピラミッドではない
図5.2.1を黄金ピラミッドとします。すると上の (4) で計算したように

が成り立ちます。すると
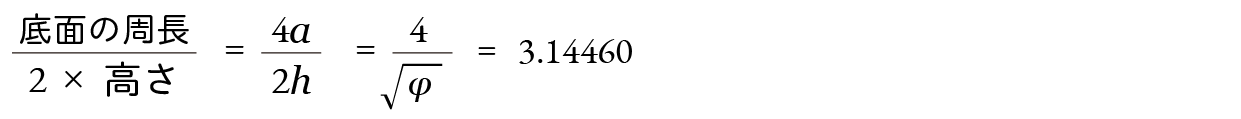
となります。3.14460 は π に非常に近いのですが π ではありません。
円周率ピラミッドについても同様なのですが、すでに計算をしているので、練習問題としてやってみましょう。円周率ピラミッドを考えます。高さを h、底面の1辺を a とします。すると
4a 2h = 2a h = π
ですから、上で計算したように
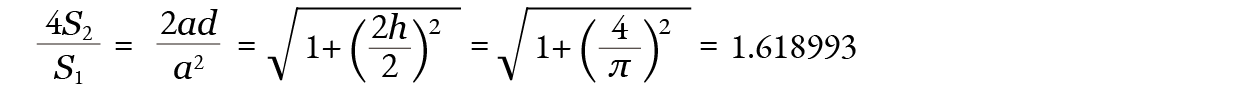
となり、黄金率に非常に近いのですが、正確には黄金率ではありません。
事実3 は数学的事実ですから疑問の余地はありません。事実3とその証明より、「円周率ピラミッドは近似的には黄金ピラミッドとみなすことができるが、数学的には等しくない」ということが分かりました。数にはこういった不思議な現象がたびたび起こりますが、これは全くの偶然であり、等しいことを証明することはできません。
前節では、セケド 5;1 2 は円周率の謎を満たすように決められたという説を述べました。もしこれを認めるなら、事実2 より黄金比の謎は自動的に満たされます。したがって、「黄金比の謎」は偶然にそうなったということになります。もちろんその逆も成り立ちますが、「エジプト人は黄金比のことを知っていた」ことを示すためには、ピラミッド以外の別の理由を探さなければなりません。
黄金比と黄金ピラミッドの特徴
黄金比は美しい性質を持っているので、黄金比を持つ構造はいろいろな解釈ができることがあります。これがいろいろな数の不思議を引き起こしているのかもしれません。黄金比の謎も、上で述べたのと違った表現で述べられることもあります。これらは簡単な数学の問題ですから、興味のある人は練習問題として解いてみてください。黄金ピラミッドに関して次が成立します。
命題1 ピラミッドは黄金ピラミッド
⇔ 側面の三角形は高さを1辺とする正方形に等しい
⇔ 「底辺の1辺の半分 : 側面の三角形の高さ」は黄金比
証明
図5.2.1 のピラミッドを考えます。底面を S1、側面の一つを S2 とします。すると上の命題は次のように言い換えられます。
黄金ピラミッド ⇔ S2 = h2 ⇔ a2:d は黄金比
ピタゴラスの定理より、
d2 = (a 2) 2 + h2
が成立し、S2 = ad 2 ですから
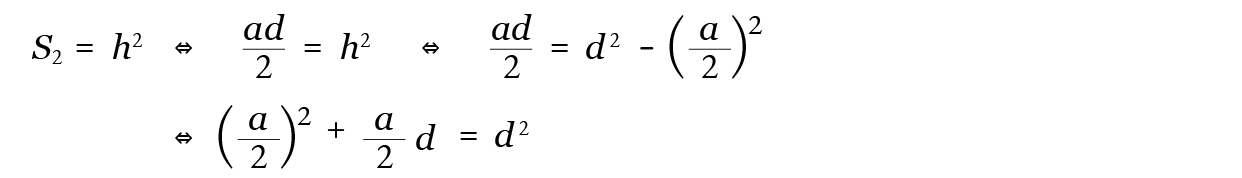
最後の式の両辺を (a 2)2 で割って、x = 2d a と置くと 1 + x = x2 となります。『4-3.黄金比とはなにか』で述べたように、方程式 1 + x = x2 の正の解が黄金率 φ です。よって次が得られます。
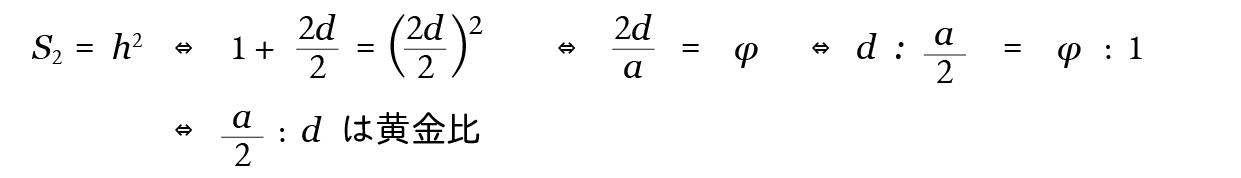
黄金ピラミッドとは S1 : 4S2 が黄金比となるピラミッドのこと、つまり 4S2 S1 が黄金率となるピラミッドのことです。4S2 S1 = (4×ad 2 )/a2 = 2d a ですから、上の続きで
2d a= φ ⇔ 4S2 S1 = φ ⇔ ピラミッドは黄金ピラミッド
となり、命題1 が証明されました。
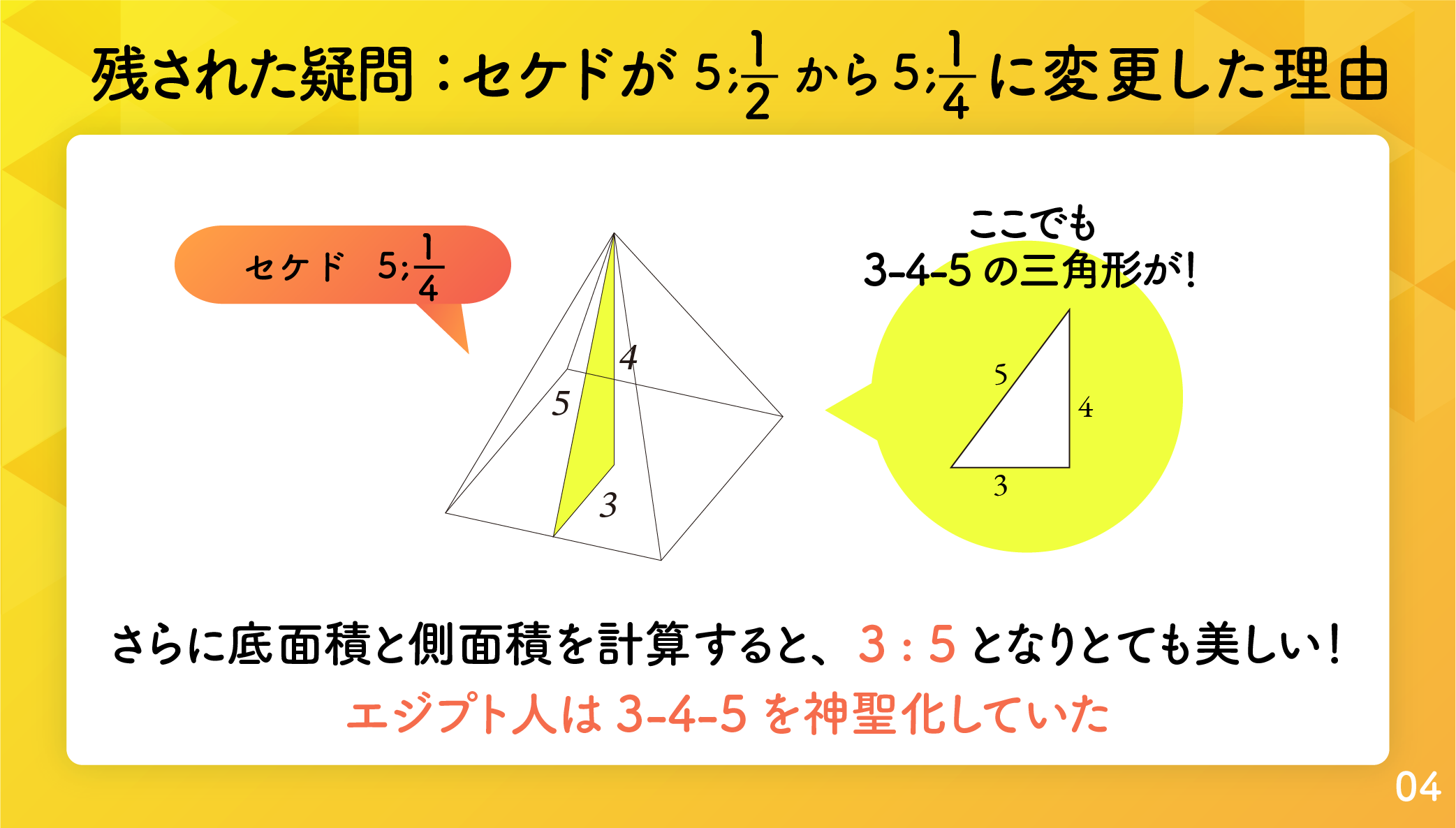
なぜセケド 5;1 2 からセケド 5;1 4 に変更したか
セケド 5;1 2 のピラミッドは円周率の謎を満たすことが分かりました。また、数学上の偶然で、黄金率の謎も満たします。では、セケド 5;1 4 のピラミッドはどうでしょうか。クフ王の後継者のカフラー王のピラミッドはセケドが 5;1 2 ではなくて 5;1 4 となっています。また『5-1』の表1 にはセケド 5;1 4 のピラミッドが 6 個も、53°も含めると 7 個あります。『3-2.比と傾き』で述べたパピルスに出てくる問題3.2.2と問題3.2.3は、セケド 5;1 4 のピラミッドを扱っています。このセケドには何か秘密が隠されていそうです。せっかく正円錐を忠実に模倣するように、ピラミッドのセケドを 5;1 2 と定めたのに、なぜセケド 5;1 2 をやめてセケド 5;1 4 に変更したのでしょうか。
セケド 5;1 4 を傾きに直しましょう。傾きは「セケドの逆数を7倍」すれば得られます。
傾き =7 21/4 = 7 × 4 21 = 4 3
セケド 5;1 4 は傾きに直すと 4 3 です。傾き 4 3 の直角三角形の斜辺はピタゴラスの定理より
= = 5
となります。つまり3辺とも整数となります。図5.2.2 参照。
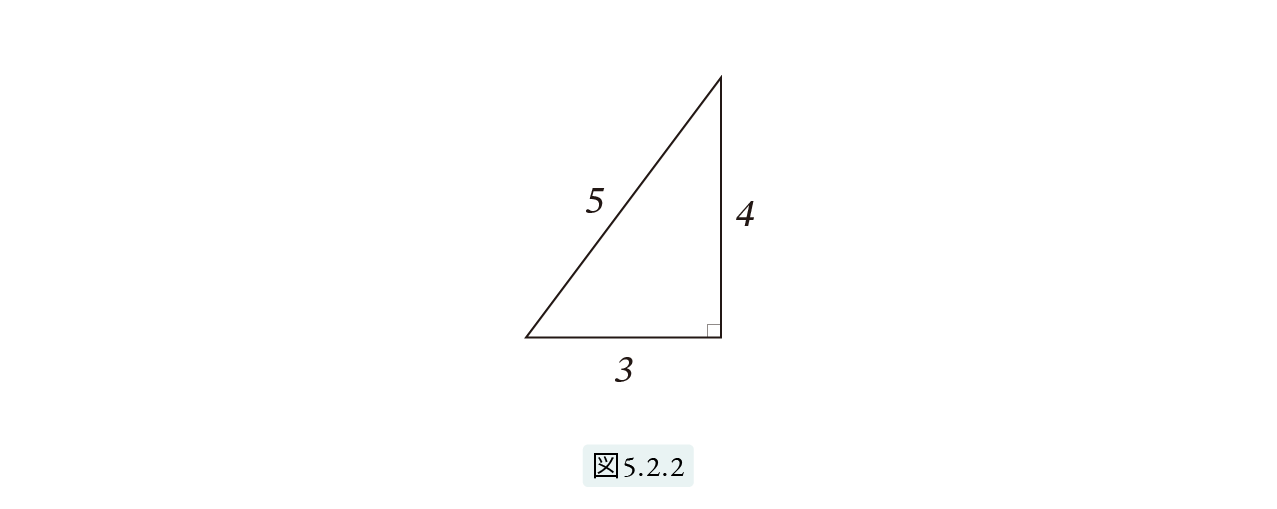
ここで現れたのはこれまで何度も現れた 3 – 4 – 5 のいわくつきの三角形、縄師が直角を作るために使ったといわれる元祖ピタゴラスの三角形とも呼ばれる直角三角形です。やはりエジプト人はこの三角形に執着していたと言わざるをえません。
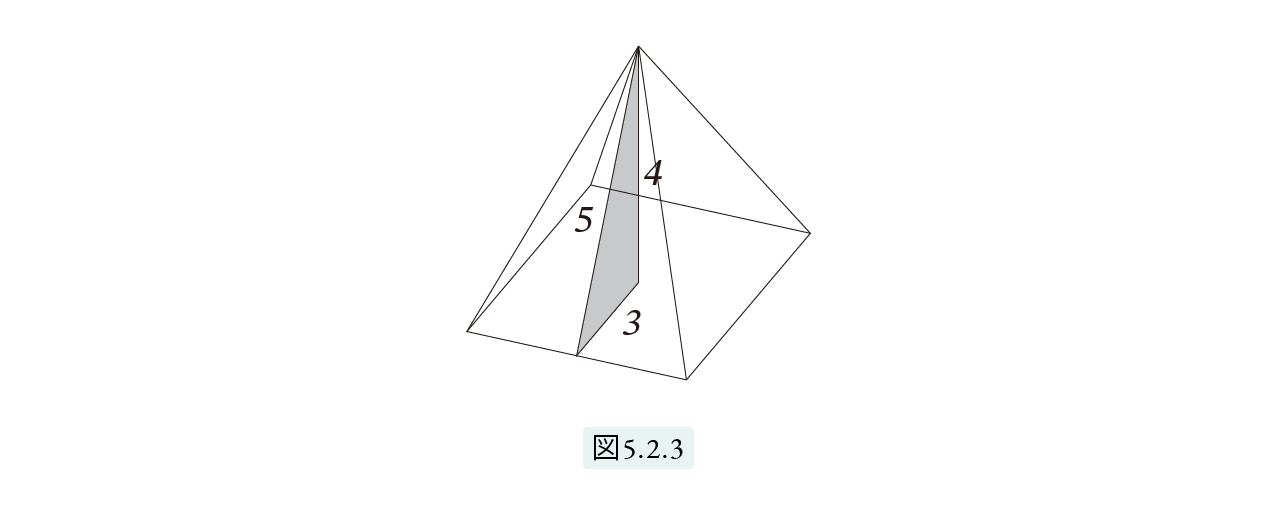
セケド 5;1 4 のピラミッドに対しピラミッドの謎がどうなるか調べてみましょう。図5.2.3のように、底面の1辺を6、高さを4 とします。まず円周率の謎から見てみましょう。
円周率の謎 底面の周長は高さを半径とする円周に等しい。
底面の正方形の周長は 4 × 6=24 です。古代では、よく円の円周を直径の3倍で計算しています。半径が4なら直径は8ですから 3 × 8 = 24 となります。したがって、円周率を3とするなら、円周率の謎が成り立ちます。
ギリシア人は円を厳密に定義し、円の幾何学的な性質を調べましたが、ギリシアの幾何学には数値が現われません。ギリシア人にとって、円は数学の対象であったのに対し、エジプト人にとって円とは現実の丸太とか円柱など現実の対象であり、円周とか面積が大きな関心事でした。仮説2 を認めるなら、エジプト人は円周が直径の 31 7 あることを知っていたことになりますが、通常は直径の3倍で計算していたかもしれません。実際、バビロニア人は円周が直径の 25 8 倍であることを知っていましたが、普通は直径の3倍で計算していました。『4-6.古代ローマとルネサンス』で述べた古代ローマの数学者ウィトルウィウスも円の扱いはとても不正確でした。古代人にとっては、円周率が 3 でも 31 7 でも31 8 でもたいした違いがないと思っていたのかもしれません。エジプト人にとってはむしろ円周率を 31 7 とするより 3 とした方が円周も自然数となるので“神秘の力”があると感じたのかもしれません。
関連記事以下の記事で詳しく解説しています++。
仮説2 エジプト人は直径 R の円周を 22 7 R で計算していた。
次に黄金率の謎を見てみましょう。
黄金率の謎 底面積 : 側面積 は黄金比である
もう一度図5.2.3 を見てください。辺の長さはすべて整数なので計算しやすいと思います。
底面積 = 6 × 6 = 36
側面積 = 4 × ( 6 × 5 ) / 2 = 60
よって 底面積 : 側面積 = 36 : 60 = 3 : 5
はたしてエジプト人は黄金率の謎 という謎に気づいていたのでしょうか。この謎には側面積が関係しています。もう一度セケド 5;1 2 のピラミッドに戻って見てみましょう。セケド 5;1 2 を傾きに直すと 14 11 です。底辺 11、高さ 14 の直角三角形の斜辺の長さは、ピタゴラスの定理を使うと
=
となり、整数にはなりませんし、この計算はエジプト人の計算能力を超えるものだと思われます。クフ王の大ピラミッドは、現代人から見れば黄金率の謎 を満たすことはわかりますが、エジプト人が実際に大ピラミッドの側面積を計算することはなかったと思われます。もし計算したとするなら、側面の三角形の高さを実際に測らなければなりません。さらにエジプト人は“黄金比”という概念も“黄金率”という概念もおそらく持っていなかったと思われます。したがって、黄金比の謎は近世に入ってから言われだしたものだと思います。しかし、まったくの創作なのでしょうか。何かもとになる言い伝えはなかったのでしょうか。
セケド 5;1 2 のピラミッドよりセケド 5;1 4 のピラミッドが優れているとエジプト人が考えたのは、側面積が整数で表されるということと、ピラミッドの断面に 3 – 4 – 5の元祖ピタゴラスの三角形が現れるということだと思われます。古代人は現代の私たちが思っているよりもはるかに自然数にこだわりを持っていたのではないかと思います。
前に述べたように、ピラミッドは正円錐をモデルとしたものであり、正円錐は半球、つまり天球を表すと思われます。すると、
側面=天上界、底面=地上界
と考えたのでしょう。だとすると「地上界 : 天上界」 が 3 : 5 という比で表されることになにか神秘的なものを感じたのではないかと思われます。この「地上界 : 天上界」という比に関する伝承が後世にまで伝わり黄金率の謎に繋がったのかもしれません。
エジプト人は 3 – 4 – 5 の三角形を神聖視していたようです。これはおそらく、自然数の順番に並んだ列 1, 2, 3, 4, 5 の最初の2つをとった数列だからだと思います。3-4-5 が神聖なら、3-5 も神聖だと感じておかしくありません。したがって次を仮説として採ることにします。
仮説3 エジプト人は 3 : 5 を“聖なる比”と考えていた
5/3 = 1.666… は黄金率 φ= 1.61859 と比べて少し違いますが、古代エジプト人もギリシア人も黄金率 φ という数値についてはなにも知らなかったことに注意してください。何しろ無限小数はおろか、小数でさえそれを表す言葉も文字も持っていなかったのですから。
エジプトの神殿や壁画や彫像などに、黄金比が現れるといろいろな著作に書かれています。本節では、エジプト人は黄金比も黄金率も知らなかった可能性が高い、と考えました。したがって、次回以下では、比 3 : 5 は黄金比とは呼ばず聖なる比と呼ぶことにします。ギリシア時代においても、ミロのヴィーナスやパルテノン神殿などに、黄金比が認められるとよくいわれます。確かに『原論』では外中比(=黄金比)のいろいろな理論的性質が議論されています。しかしギリシアの幾何学は、建築や彫像などに実際に適用されることはなかったと思われます。実際ギリシア人は、「幾何学は、純粋に“美しさ”を追求するものであって、実用に供せられるべきものではない」と述べています。またギリシアの幾何学(特に比の理論)が生まれたのは、パルテノン神殿が建設されたあとです。ですから古代のエジプトやギリシアの神殿や彫像に黄金比が現れているとするなら、それは黄金比ではなく“聖なる比”となります。
ヨーロッパで黄金比が取り上げられるようになったのは、ルネサンス以降です。ルネサンスの絵画には黄金比が使われているとされているものが多数あります。次回ではこれについて調べてみましょう。