ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
3-4.体積の計算
古代エジプト人はどのように体積を計算していたか
エジプト人は直方体の体積を「底面積×高さ」で計算していました。これは、体積を「1 × 1 × 1 の単位立方体がいくつ取れるか」と考えていたとすれば納得できます。しかしさらに複雑な円柱の体積も「底面積×高さ」で計算しています。この厳密で数学的な証明は2千年後のアルキメデス※まで待たなければなりません。エジプト人はどのようにしてこの計算式を思いついたのでしょうか。
前節で述べたように、エジプト人は円の面積をその円に外接する正方形の4隅を切ってできる八角形の面積で近似していました。正方形を 9×9 の単位正方形81個とみると、八角形は 63個分です。この 63 をエジプト人の好きな 64=82 とみなします。つまり、円の面積を単位正方形の合計で測っているのです。面積を単位正方形の合計とみなすことができたなら、体積を単位立方体の合計とみなすことはそれほど難しくはありません。もちろん少し粗雑な計測ですが、これはアルキメデスの円の面積の計測の原型と見ることもできます。
古代の円柱の体積の求め方
問題3.4.1直径10高さ10の円柱の体積を求めよ。
前節で述べた円の面の公式を復習します。
円の面積 = ( 直径×8 9 )2
この直径に10を代入し、高さの10を掛ければ答えの体積が出ます。エジプト人はこの計算をエジプト分数という特別な分数を使って計算していますが、現在のわれわれは通常の分数を使って計算しましょう。
(10×8 9)2 × 10 = ( 10 9)2 × 640 = (1+19 81) × 640 = 640 + 150×81 + 9 + 1 81 = 790 + 1 9+1 81
よって体積は 790;1 9;1 81 となります。
体積の単位
ここでエジプトの体積の単位について述べておきます。『3-2.比と傾き』で小麦の容量を測るのに枡という単位を述べました。枡は体積の単位で次のように定義されています。
1立方腕尺 = 30枡、 1枡= 1 30立方腕尺
1腕尺 ≒ 52 cm ですから、
1立方腕尺 = 523 cm3 ≒ 144リットル
1枡 = 1 30 立方腕尺 = 4.8リットル
エジプト人は2進法が好きなようで、(二倍枡)、(四倍枡) という単位もあります。これらはそれぞれ、枡の2倍、4倍の単位です。次の問題では答えを (四倍枡) で計算しています。
問題3.4.2直径が9腕尺で、高さが10腕尺の円柱の穀物倉庫の体積を求めよ
まず体積を立方腕尺で求めます。
( 9 × 8 9)2 × 10 = 640腕尺 3
1腕尺3 = 30枡、4枡= 1(四倍枡) ですから
640 腕尺3 = 19200 枡 = 4800 (四倍枡)
となります。
エジプト人は、直方体の体積だけではなく円柱の体積まで考えていたのです。こんどは本連載の目的であるピラミッドの体積について述べましょう。
切頭ピラミッドの体積
通常ピラミッドといえば底面が正方形なのですが、この節では都合により底面が長方形のものもピラミッドと呼ぶことにします。正確にいうと、ピラミッドとは、頂点から底面に下ろした垂線の足が長方形の対角線の交点にくる四角錐のことです。図3.4.1。
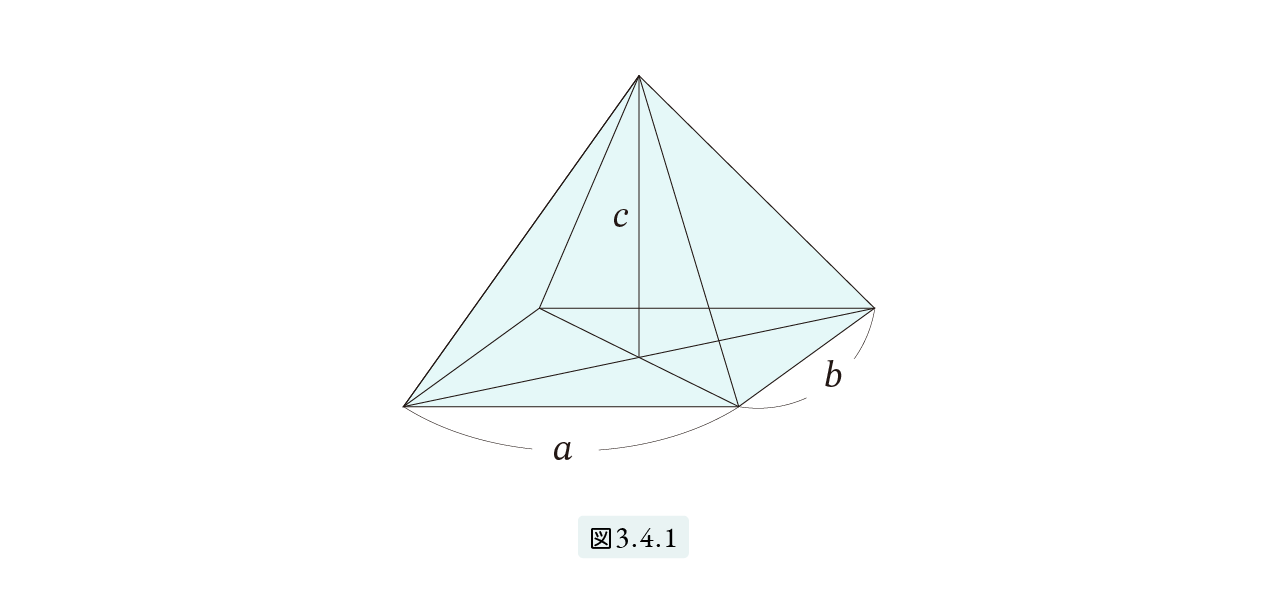
エジプト人はピラミッドの体積が
体積 = 1 3× 底面積×高さ (1)
で計算できることを知っていたと思われます。というのは、ピラミッドよりさらに複雑な、底面に平行な平面で頭部を切り取った「切頭ピラミッド」の体積を計算しているからです。エジプト人がどのようにして公式 (1) を得たかは後回しにして、まず切頭ピラミッドについて述べましょう。エジプト人が切頭ピラミッドの体積を求める公式を知っていたことは、出土したパピルスに書かれていた次の問題から分かります。
問題3.4.3上面が 2 × 2、底面が 4 × 4、高さが 6 の切頭ピラミッドの体積を求めよ。
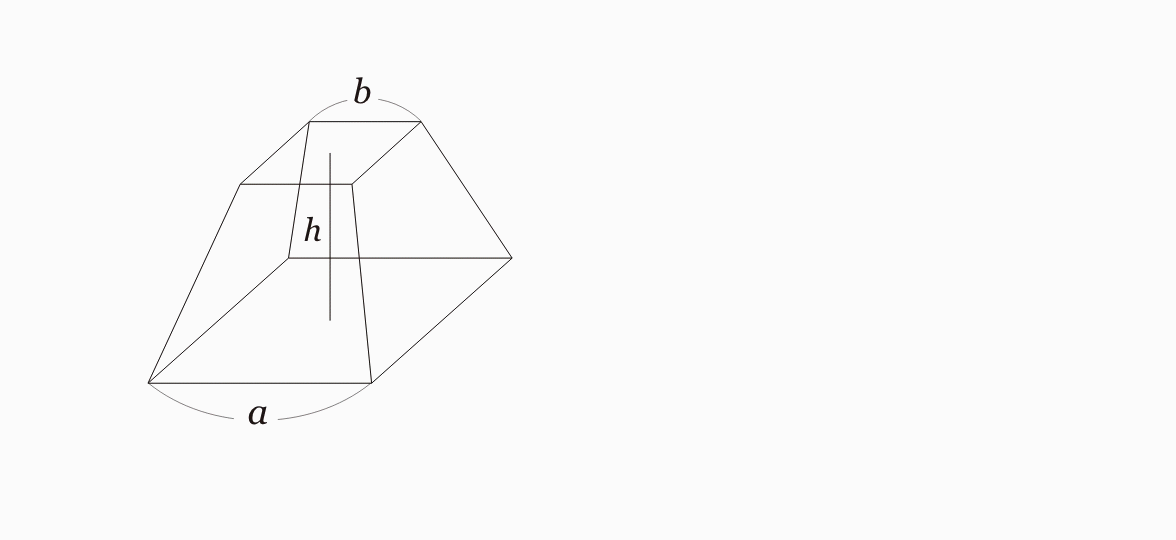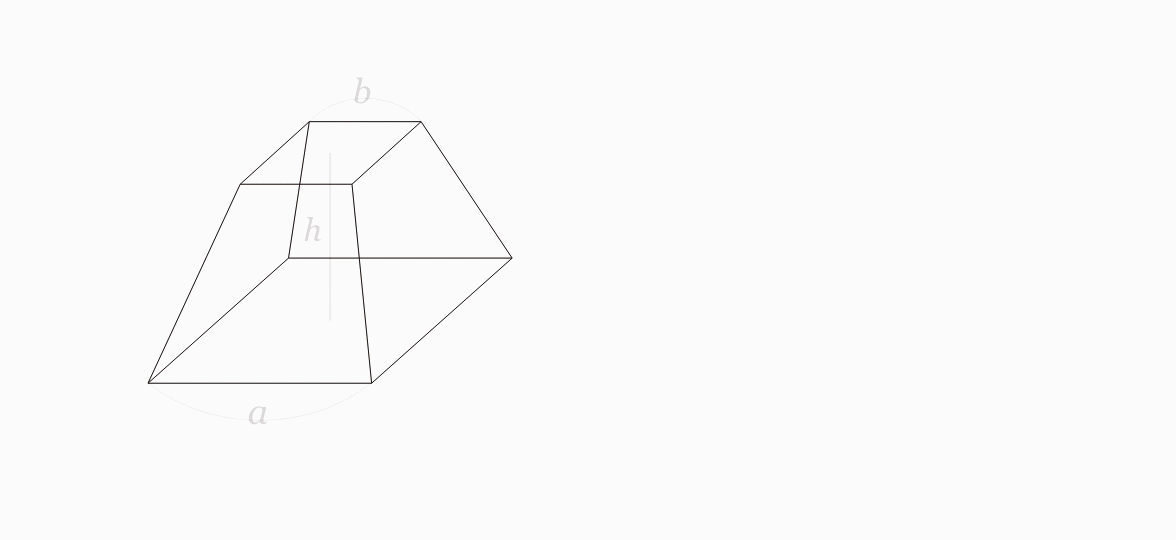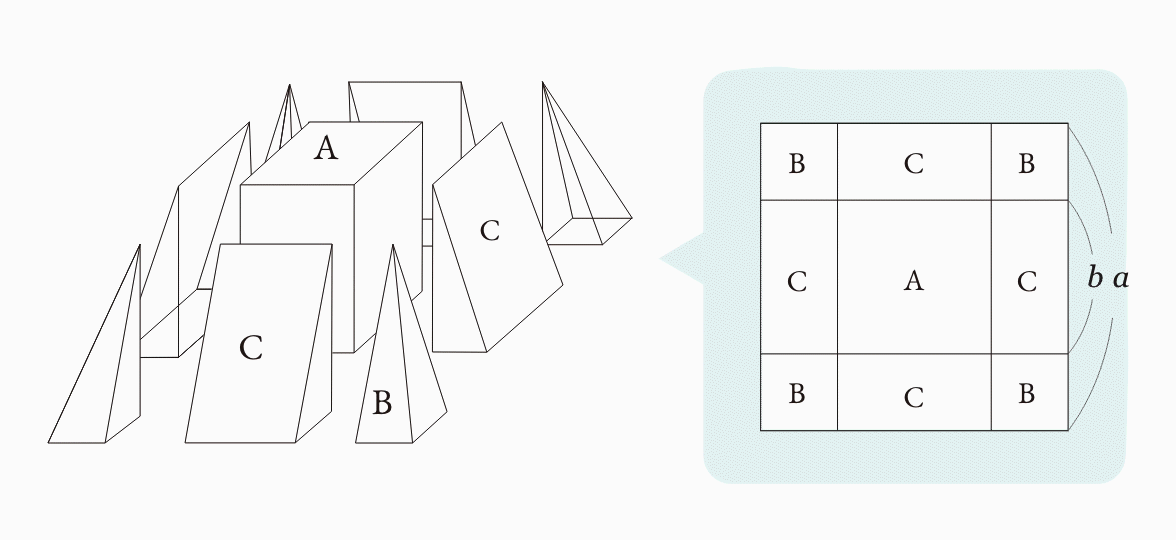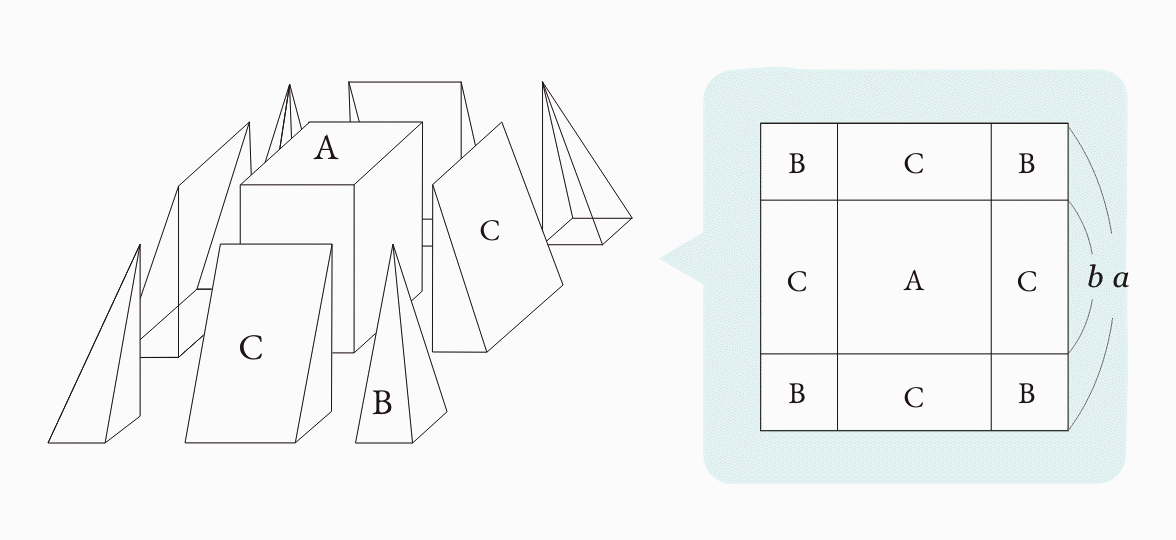
パピルスには体積を求める手順が、数値の4, 2, 6 を使って述べられています。古代では a, b, c などの記号を使えませんから 4, 2, 6 と具体的な数値で説明していますが、これは他の問題のときと同様、特定の数値ではなく一般の数値を表していると考えてよいと思います。現代風に述べるなら、底辺がa、上辺がb、高さ h の四角錐台の体積 V は次の公式で計算できると述べることができます。切頭ピラミッドの場合は、上面と底面は共に正方形とします。図 3.4.2。
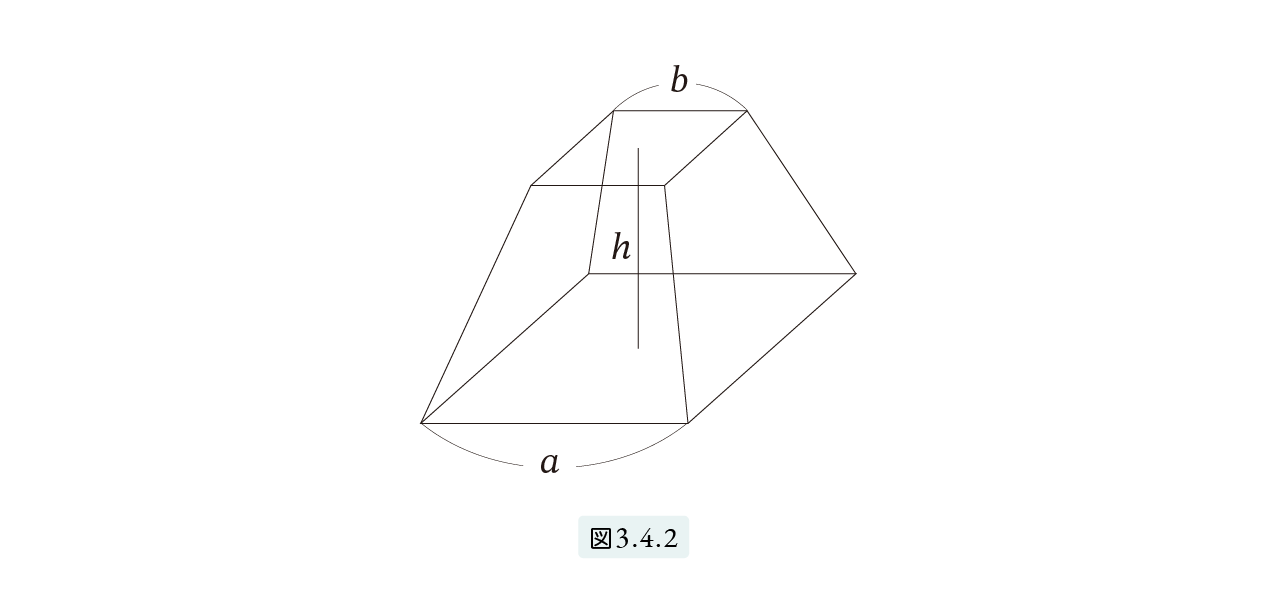
V = 1 3h (a2 + ab + b2 ) (2)
切頭ピラミッドを図3.4.3 のように切断します。真ん中に直方体が1個、四隅には四角錐が4個、4つの側面には三角柱が4個できます。
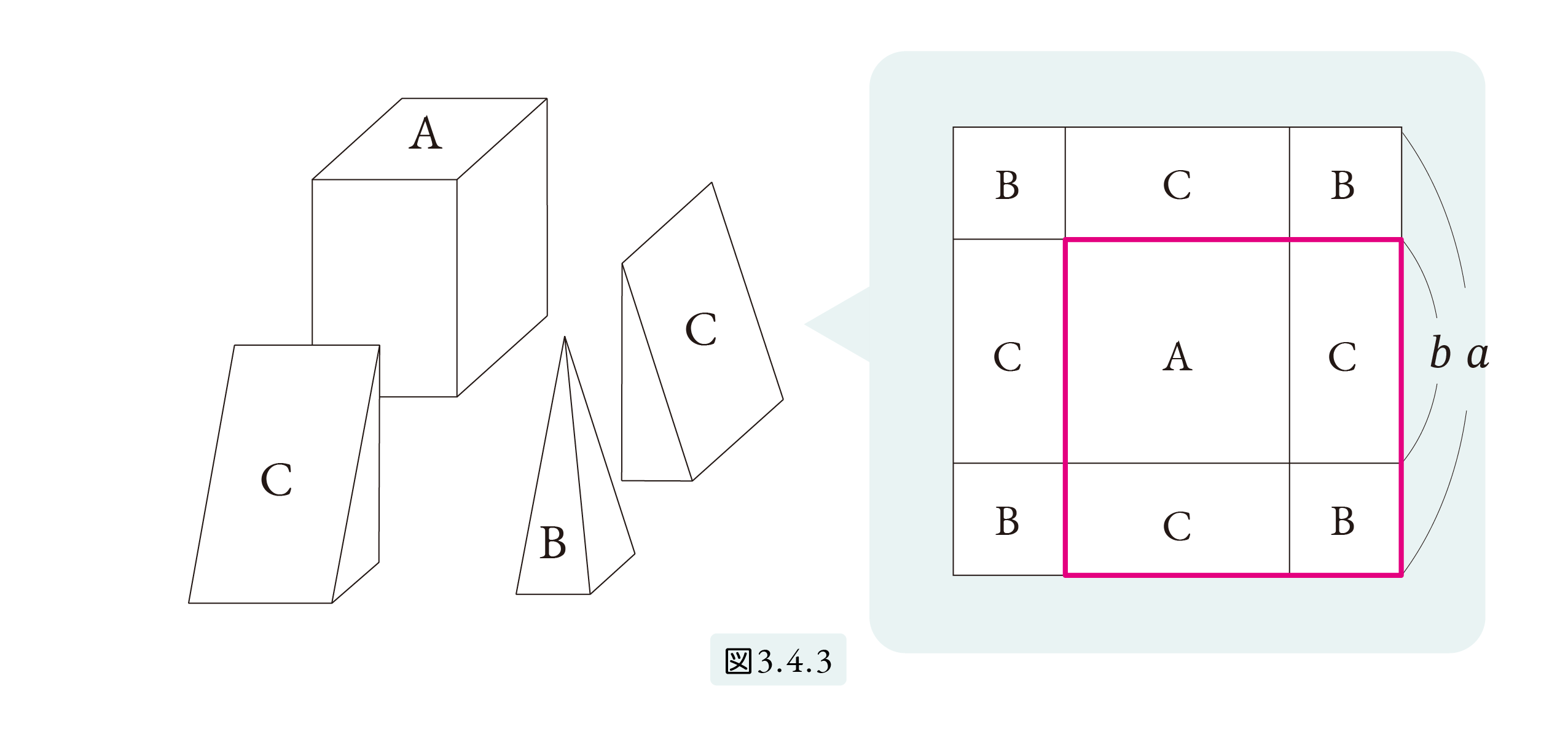
▼動画で補足しますと、以下のようになります。
四隅の四角錐を4つ合わせると、底面が (a – b) × (a – b) 高さが h のピラミッドになり図3.4.4(イ)、三角柱を2つ合わせると、底面がa – b 2× b、高さが h の四角柱になります図3.4.4(ロ)。
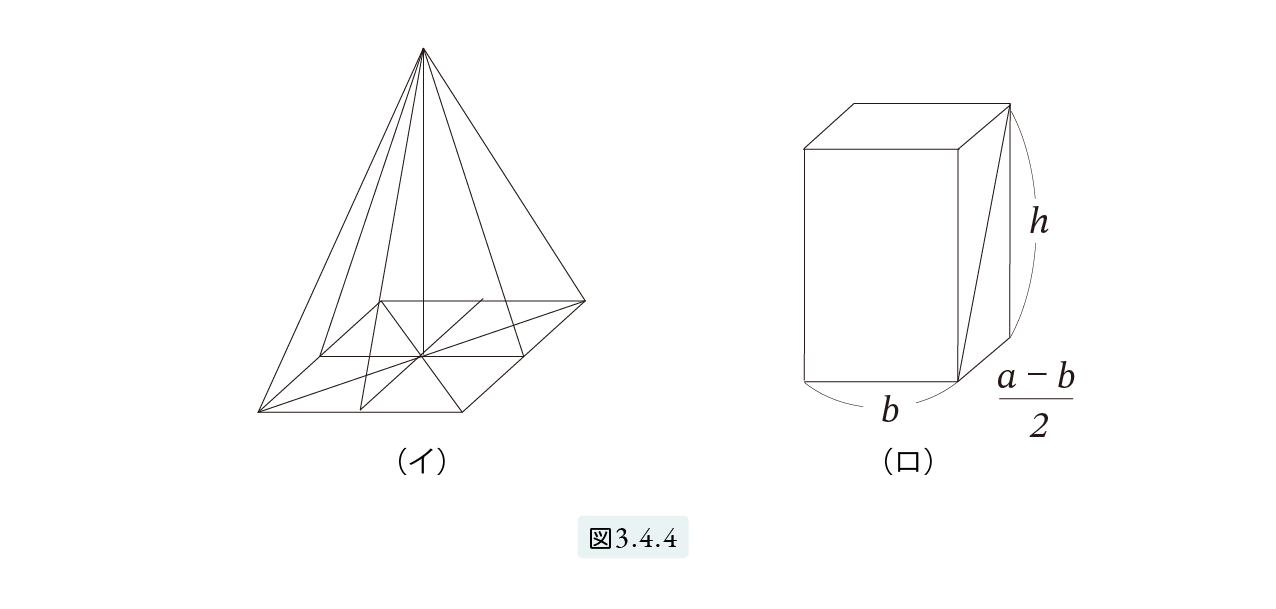
この四角柱が2個です。したがって、切頭ピラミッドの体積は
V= b2 h +2×a-b 2×bh + 1 3(a-b)2 h = 1 3 h ( 3b2+ 3ab – 3b2 + a 2 – 2ab + b2 ) = 1 3 h ( a2 + ab + b2 )
となります。
古代エジプト人は四角錐の体積の公式を知っていた
切頭ピラミッドの体積の公式 (2) の求め方はほかにも考えられますが、ピラミッドの体積の求め方 (1) さえわかれば、それほど難しいものではないよう思えます。ではエジプト人はどのようにして (1) の公式を得たのでしょうか。これに関する史料は見つかっていません。したがって以下で述べるのは想像に過ぎませんが、おそらくこれぐらいは考えついたのではないかと思われます。
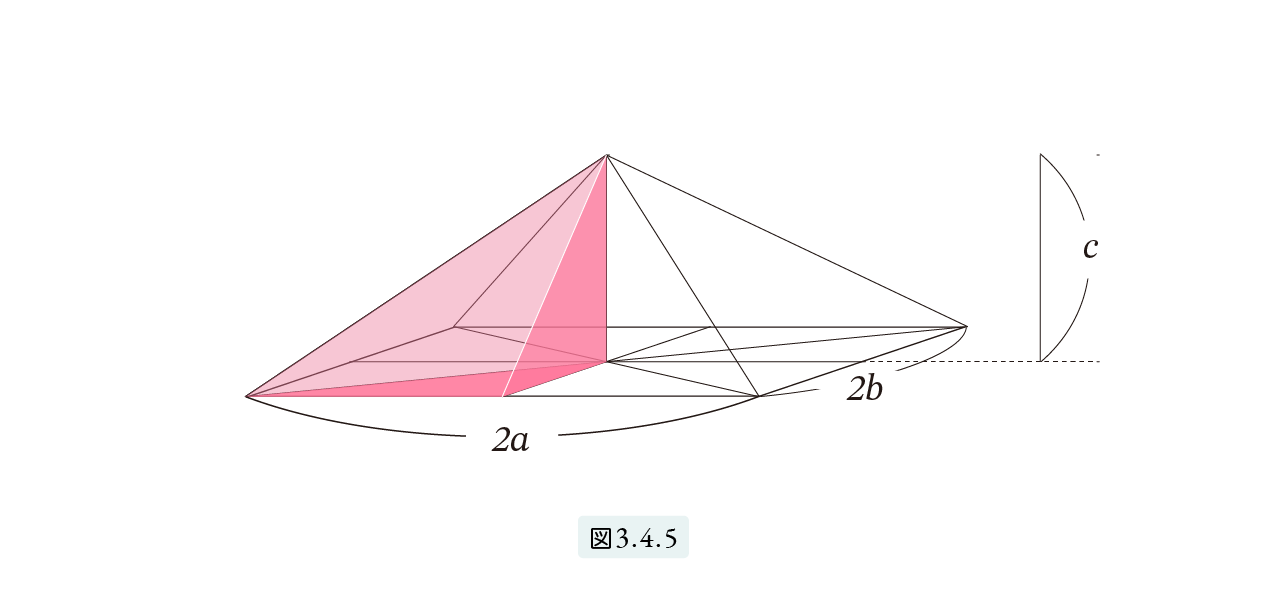
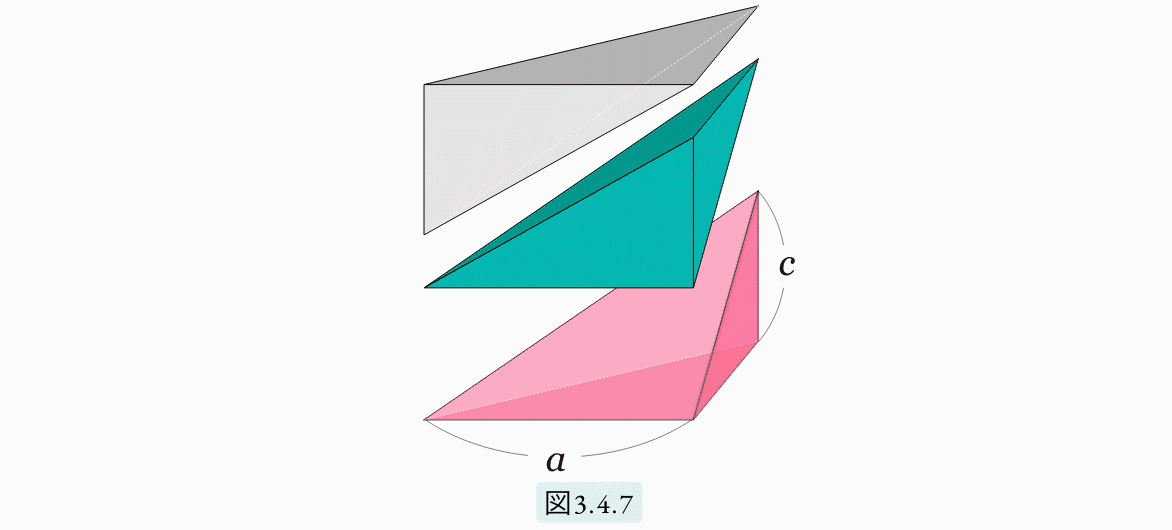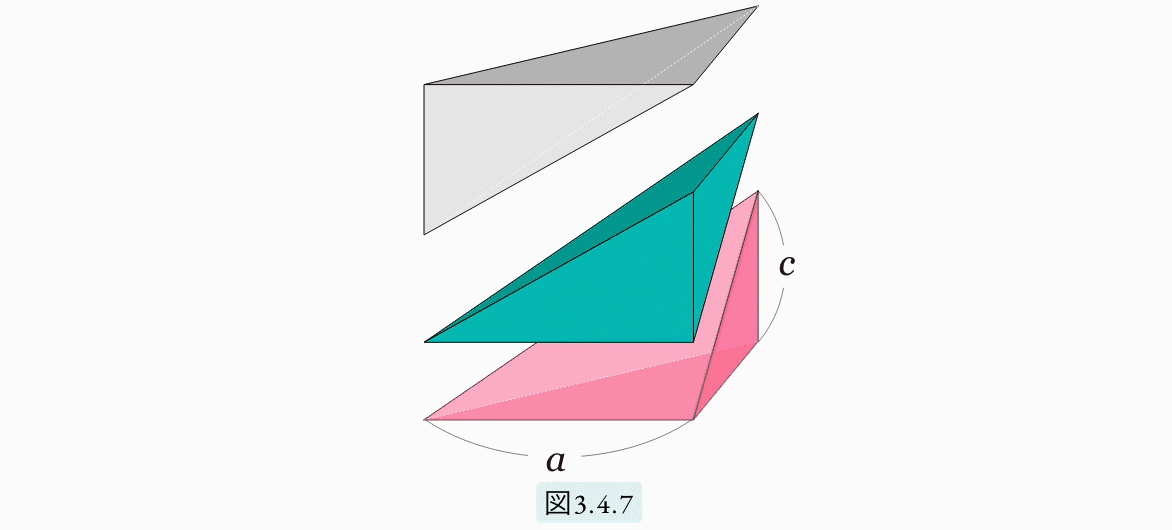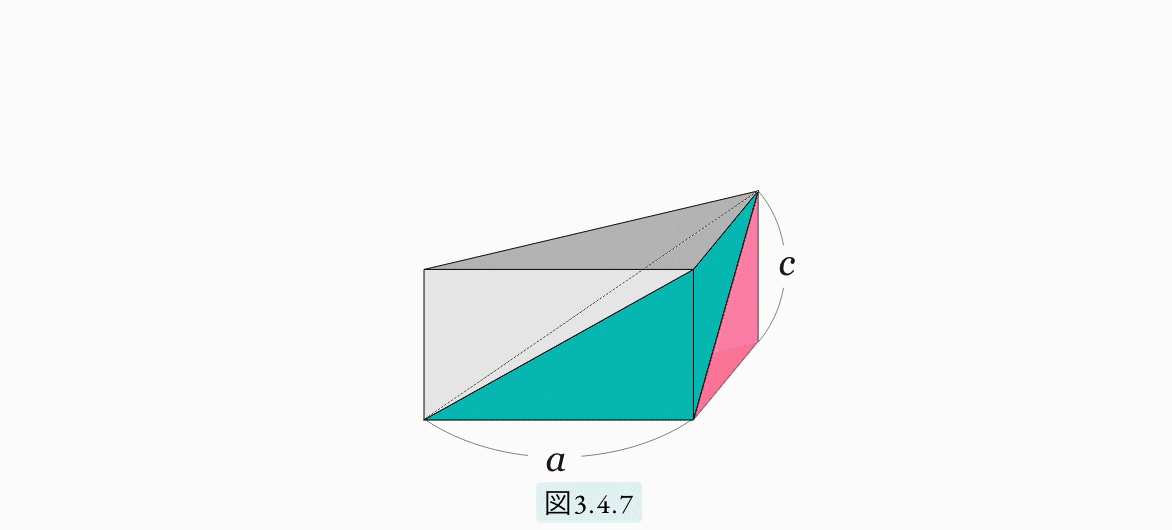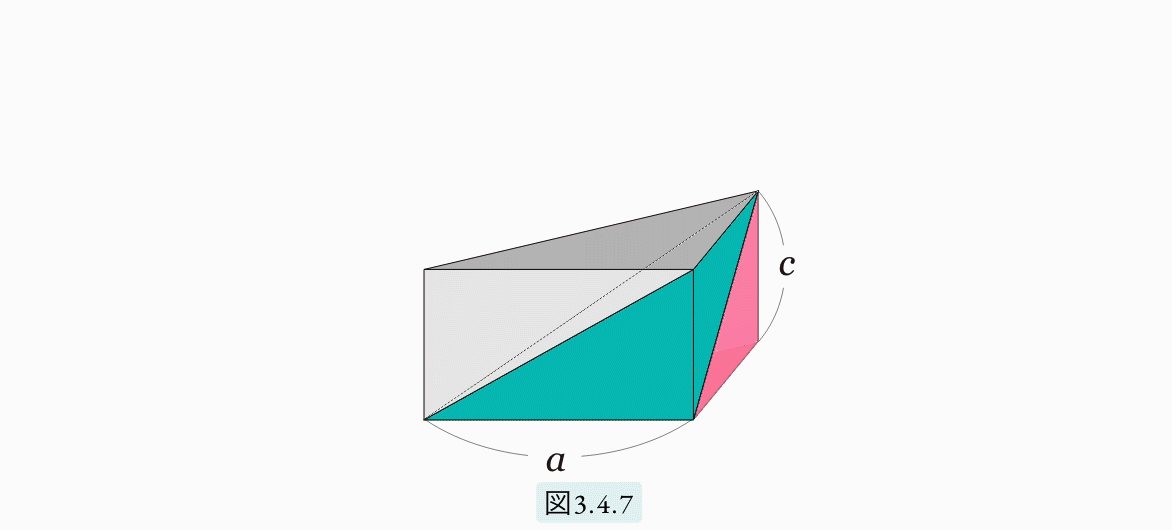
図3.4.5のような、底辺が 2a × 2b 高さが c のピラミッドと考えます。上の図3.4.4 の(イ) と同様に、このピラミッドを8個の三角錐に分割します。図3.4.5(イ) は、その8個のうちの一つを取り出したものです。底面が a×b の直角三角形、高さがc です。ここで (ロ) と (ハ) のような三角錐を考えます。この3つの三角錐をうまく組み合わせると、図3.4.7 で示されるような三角柱ができ上ります。
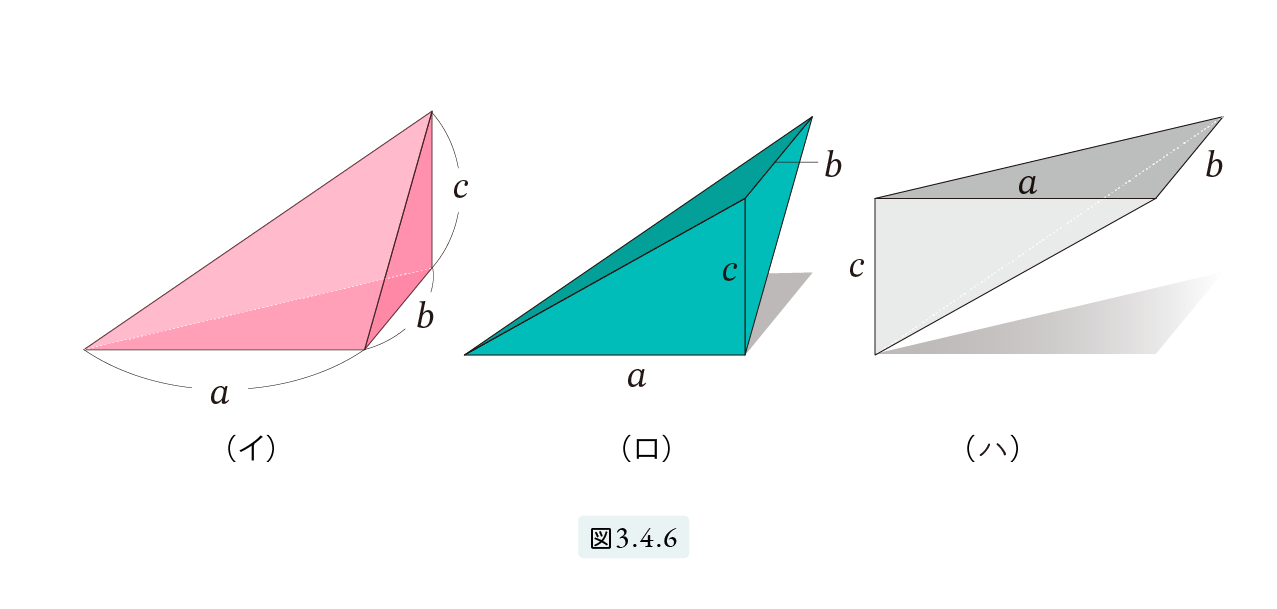
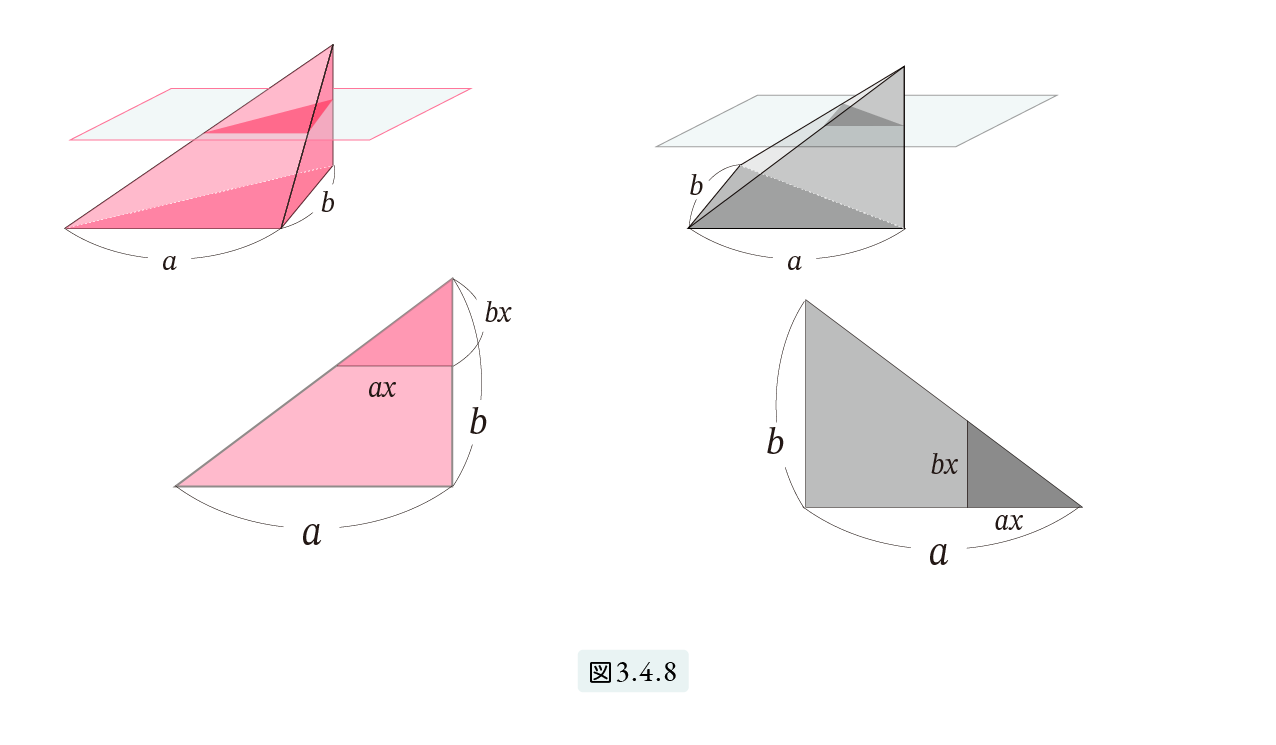
次に、これら (イ), (ロ), (ハ) の体積が等しいことを示します。まず (イ) と (ハ)。2つの三角錐を、a と b を辺とする直角三角形を底面とするように置き、底面と平行な平面で切断します。図3.4.8 は真上から見た図で、真上の頂点から cx (0<x<1) の所で切断した図です。この切断面は合同であることが分かります。エジプト人は、石を下から積むことでピラミッドを作りましたから、切断面が常に同じなら体積が同じであると判断できたと思います。
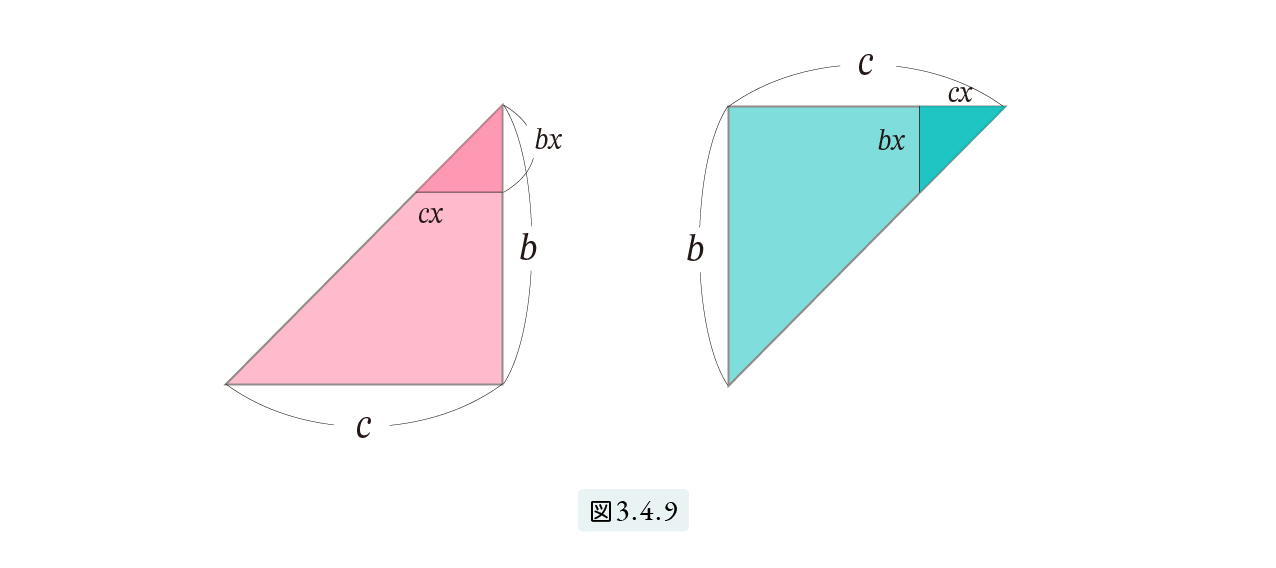
(イ) と (ロ) の体積が同じことも同様に示すことができます。こんどは b と c を辺とする直角三角形を底面とするように置きます。図3.4.9 は真上から見た図で、影の直角三角形は、上から ax の所で切断した切断面です。この場合も切断面は合同となります。
以上よりこれら3つの三角錐は同じ体積です。よって、(イ) の三角錐の体積は、図3.4.7 の三角柱の 1 3 となります。よって、
(イ) の三角錐の体積 = 1 6 abc
となります。この計算より、図3.4.5 のピラミッドを切り分けた 8 個の三角錐はすべて同じ体積 1 8abc となることが分かります。よって、
図3.4.5 のピラミッドの体積 = 1 3(2a)(2b)c
となることが示されました。
