1-1.ピラミッドの謎とは

ピラミッドに関する３つの謎

みなさん、「ピラミッドの謎」のことはご存知ですか。
昔から、エジプトには多くの人が訪れています。歴史や考古学は人気があり、ピラミッドはテレビなどでよく取り上げられています。特に有名なのはギザにあるクフ王のピラミッドで、「大ピラミッド」といえばこのピラミッドのことを指します。太古の昔から多くの人が大ピラミッドを訪れ、その巨大な姿に圧倒されてきました。大ピラミッドは今から 4500年ほど前に造られたのですが、その後ほぼ3000年もの間、表面が真っ白な石灰岩でできた化粧石で覆われ、白く光り輝いていたようです。この巨大な建造物をまのあたりにした古代の人々は、その壮大な姿に衝撃的な感動をおぼえたものと思います。「誰がこんなに美しい巨大なものを造ったのだろう。とても人間わざとは思えない。きっとこの中には、すばらしい財宝、古代の英知、あるいは神の言葉の書かれた文書があるに違いない」と、考えたに違いありません。もちろん、時代や人によって考え方は様々で、「なんでこんななんの役にも立たないバカでかいものを、たった一人のファラオのために造ったのだろう」という意見を言う人もいました。
　大ピラミッドは世界7不思議の1つといわれ、昔から多くの人が「ピラミッドの謎」について語っています。ここではその謎のなかでも数学に関係した謎を取り上げます。

第1の謎：ピラミッドには『 π 』が含まれている？

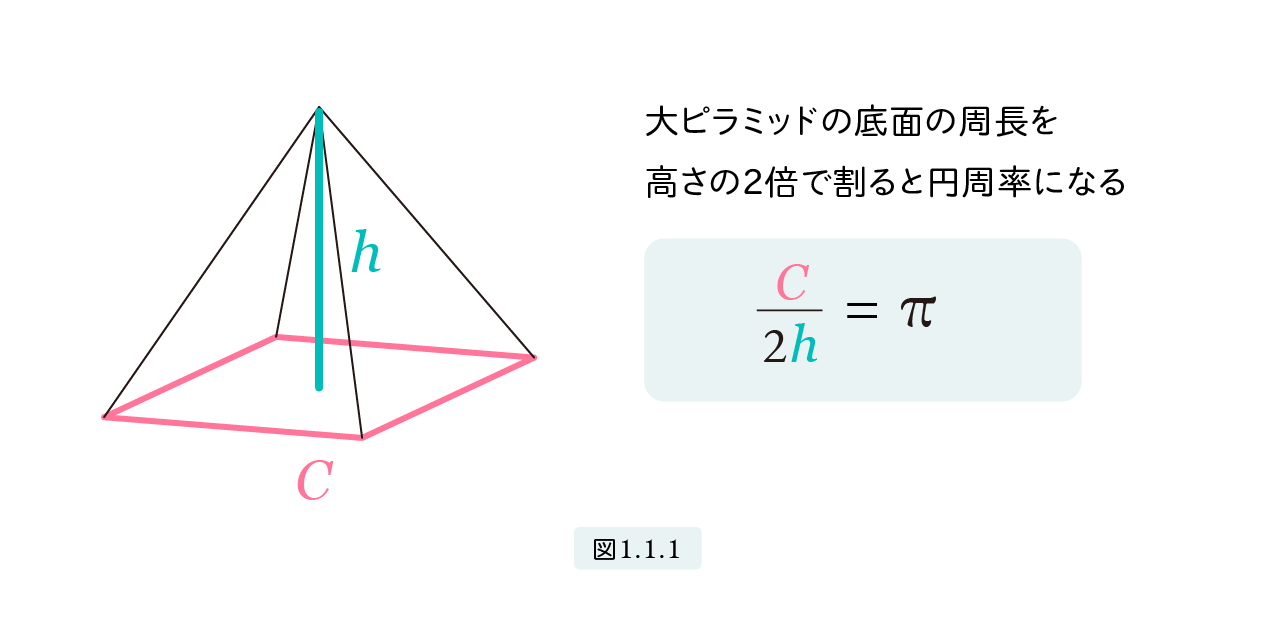
円周率の謎大ピラミッドの底面の周長を高さの2倍で割ると円周率になる

円周率とは「円周を直径で割った値」のことで、現代の皆さんなら円周率πは次の値であることを知っていると思います。

π = 3.141592654⋯(1)

では、エジプト人はこの円周率πを知っていたのでしょうか。

図1.1.1は周長が C で高さが h のピラミッドです。円周率の謎は「C 2h ＝ π」が成立すると言っています。

大ピラミッドが実際に円周率の謎を満たしていることを確かめてみましょう。大ピラミッドは今から4500年も前に作られたのだから、だいぶ風化していて正確な値はわからないと思われるかもしれません。底辺の基部は長い間砂に埋もれていて原形をとどめているようです。また、頂上部や側面は、かつては化粧石で覆われていたのに今では化粧石が剥ぎ取られ巨石のブロックが積まれた状態ですが、高さは傾斜角からほぼ正確に推測できるようです。これまで何度も測量され、計測技術も進歩して値も正確になってきています。いろいろな著作にその値が出ていて、多少の測定誤差がありますが、次のような値とみてよいでしょう。その他の測定値をとっても結果にはほとんど影響ありません。

底面の正方形の1辺： 230.37 m,　 　高さ： 146.6 m(2)

この値を使って、円周率の謎が成立するかどうかを計算してみましょう。正方形の周長を高さの2倍で割ります。

230.37×4 146.6×2= 3.142837653(3)

上の (1) と比較してみてください。驚くほど一致しています。しかし、いくら一致している方といって、“偶然の一致”というのはよくあることです。

歴史の専門家（考古学者や数学史の学者）はこの“一致”をどのように見ているのでしょうか。たいていの専門家は「円周率が現れたのは偶然だ」と考えているようです。まったくの偶然という説と、何らかの原因でエジプト人が気づかないうちにπが紛れ込んだという説があります。「何らかの原因」の代表的なものに、「長さを測るのに図1.1.2のような一輪車を使った」というのがあります。

ピラミッドの底辺のような長い距離を測るには、ロープで測るよりも一輪車の方が楽に測れますし、このように測れば計測値にπが入ってきます。たとえば半径1メートルの車輪を1回転させると車輪の進んだ距離は 2πメートルとなります。非常に説得力のある説のように思えますが、この説は欠点もあります。一つは、エジプトで車輪が使われるようになったのはこれよりも後の時代であり、計測に車輪が使われたという証拠は現在の所発見されていないことです。さらに、もし車輪が使われたとしたなら、なぜ周長を測るのに車輪を使っておいて、高さを測るのに車輪を使わなかったのかが分かりません。
　もっと本質的な疑問は「なぜエジプト人はピラミッドをあの形にしたのか」です。今回は円周率の謎の紹介だけで、このweb連載を通してこの問題の解答を述べていきたいと思います。具体的には「エジプト人はピラミッドを、周長が高さを半径とする円の円周となるように設計していた」ことを論証するつもりです。

「エジプト人が円周率を知っていたはずがない」と考えられてきたのにはわけがあります。まず、「円周対直径」の比が円によらず一定であることを証明したのは、大ピラミッドの時代より2千年もあとのギリシア数学です。つまり、数学的に円周率という概念を得たのはギリシア時代になってからだという認識です。さらに、円周率πの近似値22 7を得たのは、数学史に 燦然 さんぜん と輝くギリシアの大数学者アルキメデス※ということになっています。未開なエジプト数学で円周率22 7 が得られたはずはない、と誰もが思っていました。しかし、21世紀になってオリエントの数学（エジプト数学とバビロニア数学）が意外と進んでいることが分かってきました。

第2の謎：ピラミッドには『 黄金比 』が隠されている？

次に黄金比の謎について述べましょう。まず 次の数 φ を考えます。

φ = 1.618033989 … (4)

この φ のことを黄金率といい、比 1 : φ のことを黄金比といいます。比とは何か、黄金比とはどんな比なのか、黄金率はどのように定義される数なのか、chapter4で説明します。ここでは、黄金比とは 1 : 1.618033989… という比のことだと考えてください。黄金比の謎は次のように述べることができます。

黄金比の謎大ピラミッドの底面積に対する側面積の比は黄金比である。

底面積を S₁、側面積を S₂ とします。黄金比の謎は、 S₁ : S₂ が黄金比となること、つまり

S₁ S₂ = φ = 1.618033989 …

が成立することです。

ピラミッドの高さを h、底面の正方形の1辺の長さを 2a、頂点から底辺に垂直に下ろした線の長さを d とします。頂点から底辺に垂直に下ろした線の長さをd とします。図1.1.3 参照。

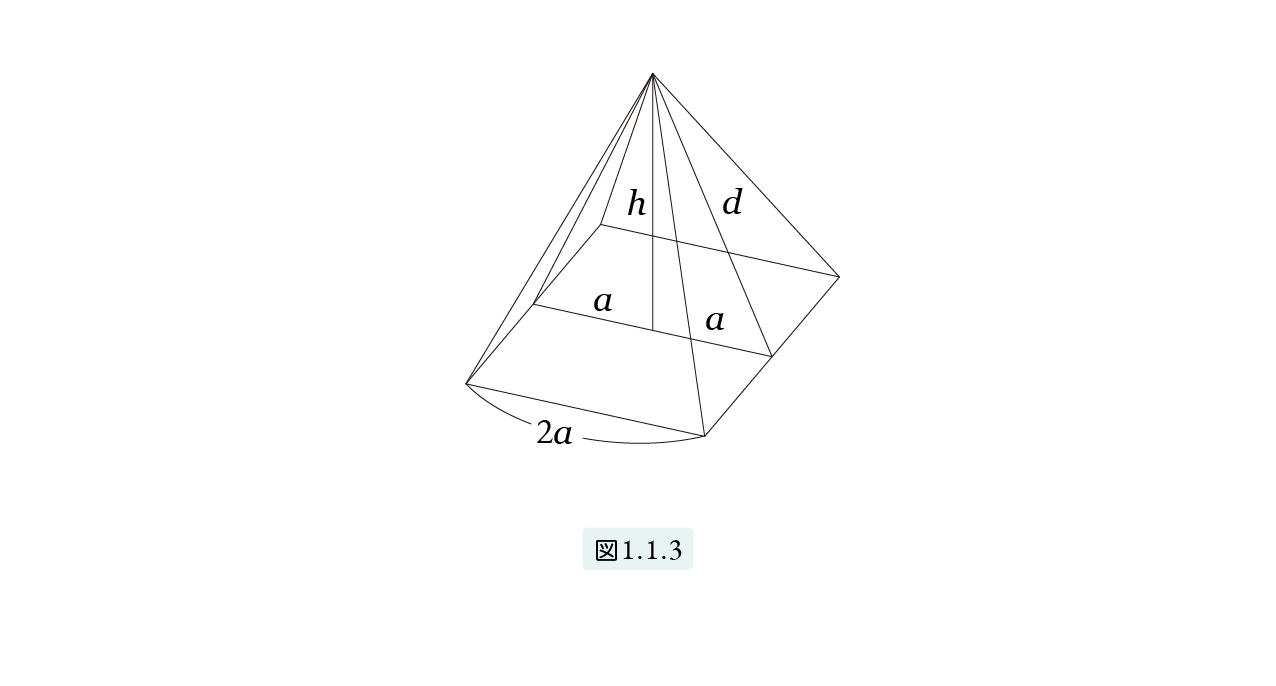
図のようにピラミッドを2つに切断すると、切断面は、底辺が 2a、高さが h の2等辺三角形となります。したがって、

底面積 S₁ = (2a)² ,
側面積 S₂ = 2ad 2 × 4 = 4ad

となります。

大ピラミッドに対し、黄金比の謎が成り立つかどうか見てみましょう。斜辺の長さ d はピタゴラスの定理より

d= $\sqrt{a^2+h^2}$

となります。

大ピラミッドの底面の1辺の長さは 2a ＝ 230.37 (m) で、高さは h ＝ 146.6 (m) です。まず d を計算すると、

d = $\sqrt{{\mathrm{115.185}}^2+{\mathrm{146.6}}^2}$ = 186.4380439

となります。したがって、

S₂ S₁ = 4ad 4a² = d a = 186.4380439 115.185  = 1.618596553 (5)

となります。これを (4) と比較してください。これはほとんど一致しているとみてよいでしょう。つまり、黄金比の謎は成り立つのです。しかしこれも円周率の謎と同様に「偶然の一致」かもしれません。また、円周率 π と同様に黄金率 φ ＝ 1.618… も無理数です。エジプト人がこのような無理数を知っているはずはありません。もし偶然でないとしたら、何か理由があるのでしょうか。

第3の謎：『 地球の緯度 』が隠されている？

大ピラミッドを測るといろいろな数値が現れます。これらの数値には天文学上の数値が隠されているというのが「天文学上の謎」です。これにはいろいろありますが、本連載ではその中で大ピラミッドの底辺は地球の大きさを表しているというものをとりあげます。正確にいいなおすと、「大ピラミッドの底面の1辺を 480 倍したものが、地球の 1緯度の長さになる」となります。地球の周長は約 4万キロです。1辺 2a ＝ 230.37 m を使って計算してみましょう。

230.37 × 480 × 360 m = 39807936 m = 39808 km

この値はほぼ 4 万キロとみてよいでしょう。しかし、「なぜ 480 倍なのか」ということと「エジプト人は、円1周が 360度という角度の単位を使っていたのか」などという疑問が生じます。それに単位もメートルで、メートルは地球の周長を基準にして決められたものです。しかし、地球の周長を測ったのは、エジプトのアレクサンドリアにいたギリシア人のエラトステネスということになっていますから、まんざら関係がないわけではありません。これについてはchapter5で議論しましょう。

ヨーロッパでは古くから、古代ギリシア時代につくられたという地中海周辺の古地図が伝わっていました。この古地図には緯度と経度が書かれていました。このことは上の「ピラミッドの底辺の長さと地球の大きさ」と何か関係がありそうです。実際次のような伝承があります。

大ピラミッドは尺度の基準を不朽のものにするために造られた

この謎は、大ピラミッドが何らかの尺度の基準であったか、あるいは地図上の基準であったのではないかということを想像させます。これについてはchapter5で議論します。

ピラミッドの謎については、上で述べたもののほかに土木工事の謎があります。土木工事の謎は、あれほど巨大な建造物を古代エジプト人が本当に造ることができたのか、もしできたとするならばどのようにして造ったのか、という謎です。一般にはこれが一番よく取り上げられていて、歴史の専門家が検討していますが、どうやら古代のエジプト人でも可能だという結論のようです。円周率の謎と黄金比の謎についてはどうでしょうか。エジプト人自身が円周率や黄金率を知っていて、地球の周長を計測したという説は（おそらく）ないと思います。となると、考えられるのは次の2つです。1つは、エジプト人がエジプト人以外の高度な知能をもった人（または神）から教えてもらったというもの。エジプト人以外の高度な知能というのは、「神の啓示」、「超古代文明」、「地球外生命」と3つあります。おそらく近世までは、「神の啓示説」が一番有力だったと思います。各国の神話には「火などの知恵を神から授かった」というお話が残っています。「超古代文明説」は、今から1万年以上前に進んだ文明が栄えていたという説で、これも古くからあります。現代では、「神の啓示説」の人気がなくなり、その代わりに「地球外生命説」、つまり宇宙人から教わったという説が浮上してきました。

歴史の専門家（考古学者や数学史の学者）は、このような説は採りません。専門家は、たとえば円周率の謎を例にとると、「円周率が現れたのは偶然だ」と唱えます。まったくの偶然という説と、何らかの原因でエジプト人が気づかないうちに π が紛れ込んだという説があります。

まとめ

数に関しては昔からとても不思議な現象がいくつも報告されています。いかに起こりそうもないことでも、偶然に起きることはあるのです。しかし、その現象が「なぜ起きたのか、どのようにして起きたのか、ということの合理的な説明」があれば、偶然説よりその説の方が支持されると思います。さらにそれと同じ現象が他でも起きていることが分かれば、もはや偶然説よりはその説の方に大きな支持が集まると思われます。本連載では上で述べた３つのピラミッドの謎について、「偶然説」ではない別の見方をします。上で述べたように、ピラミッドにはとても多くの偶然の一致があります。本当にすべてが偶然なのでしょうか。皆さんもいっしょにピラミッドの謎について考えてみませんか。