ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
5-2.ピラミッドの『円周率の謎』を解明する(2)
前回の記事では、ピラミッドはセケド(傾き)を基準に作られていたこと、またそのセケドの値とピラミッドの円周率の謎の関係性について述べました。また、『セケド5;1 2の四角錐』は、ピラミッドの円周率の謎 (底面の周長を高さの2倍で割ると円周率になる)を満たす立体であるということを証明しました。今回は、この説に残る何個かの疑問点のうち、ひとつめの疑問を明らかにしていきます。
なぜセケド5;1 2を基準にしたのか。切りのいいセケド5を選ばなかった理由。
なぜセケド5;1 2から5;1 4に変更したのか。(次回解説)
ページ目次
スネフェル王の崩れピラミッドと「ベンベン」
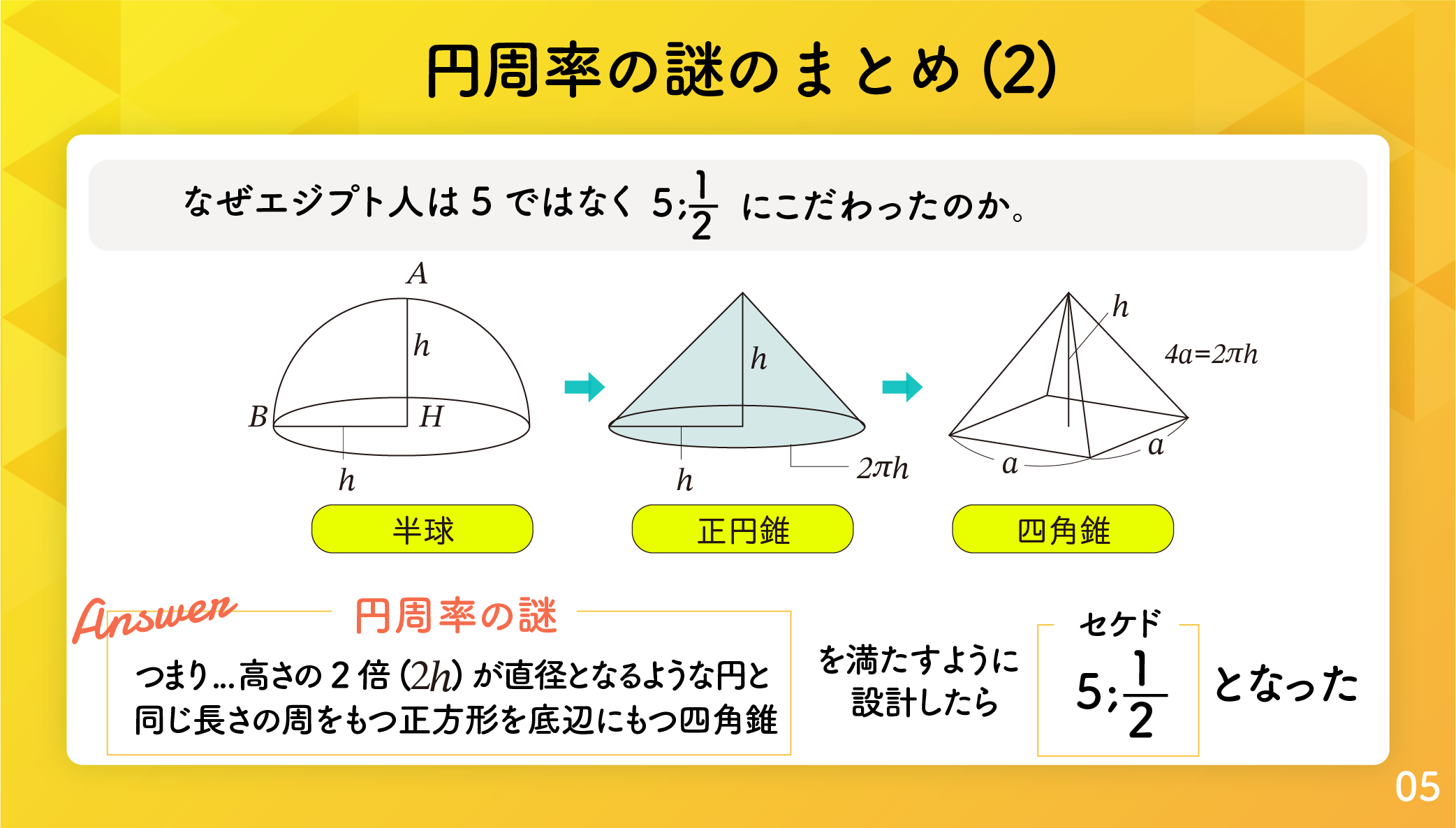
古代エジプトでは自然はマアト(秩序)によって支配されており、数には神秘的な力があると信じていました。セケドを 5;1 2 とか 5;1 4としたのは偶然ではなくなにか意味があるはずです。
事実1 より、「セケドを 5;1 2 に決めたから円周率の謎が成立した」という推論もできますが、それでは「なぜセケドを 5;1 2としたか」という謎が残ります。ここでは逆に、「円周率の謎が成立するようにピラミッドを作ったら、セケドが 5;1 2 となった」という方針で、推論を進めましょう。
ピラミッドが作り始められたのは第3王朝からで、本格的なピラミッドが作られるようになったのはクフ王の父のである第4王朝の初代の王スネフェルからのようです。スネフェルは巨大な権力を持ち、ピラミッドを3つも作っています。これらは「屈折ピラミッド」、「赤のピラミッド」、「崩れピラミッド」と呼ばれています。なぜ3つも作ったのか、歴史の専門家の間でも議論されています。専門家の意見を聞いてみましょう。
『世界の歴史4-オリエント世界の発展、小川英雄、山本由美子、中央公論社 (2009)』のなかで、この本の著者は次のように述べています。
これらの3つのピラミッドは「屈折ピラミッド」、「赤のピラミッド」、「崩れピラミッド」の順につくられたと考えられます。後で述べる理由により、王はピラミッドの傾斜角は52度が理想であると考えました。最初の屈折ピラミッドは、底面の1辺が189メートル、高さ101メートルで、途中高さ49メートルまでの勾配は54度31分、それより上は43度21分です。途中で勾配が変わるので屈折ピラミッドと呼ばれます。次に作られたのが、鉄分の多い赤い石灰岩で造られた赤のピラミッドで、底面の一辺219メートル、高さ99メートル、勾配は43度36分です。両方とも理想とする角度の 52度とかけ離れています。それで最後に作ったのが、底辺144メートル、高さ92メートル、勾配51度51分の崩れピラミッドでであったと推測しています(現在は無残にも崩れているので、崩れピラミッドと呼ばれています)。また、なぜ52度にこだわったかというと、聖都ヘリオポリス※にあった聖石「ベンベン」を手本としたためであると述べています。
ヘリオポリスという名はのちにギリシアの人が付けた名前で、ギリシア語で「太陽の都」という意味です。ヘリオポリスは太古からの太陽信仰の中心地で、不死鳥で有名なフェニックス神殿がありました。この神殿には昔から伝わる秘密の文書や歴史に埋もれた謎の物体が保管されており、ここの高位の神官は「天文学者の長」とよばれ、天文学と占星術を行っていたようです。クフ王もここにたびたび訪れ秘密の文書を探したと伝えられています。ここには、古代エジプト語で「ベンベン」とよばれる聖なる石が長らく保管されていたようです。この「ベンベン」とは何でしょうか。研究者はこれを隕石だとみています。古代では、空から落ちてくる隕石を「太陽の分身」とみて御神体とすることがよくあります。注意すべきことは、この形状が「先の尖った円錐形」をしていたという伝承があることです。ピラミッド・テキストにも側面がでこぼこした石として描かれています。研究者のなかには、この「円錐形がピラミッドのモデルになった」とみる人がいます。
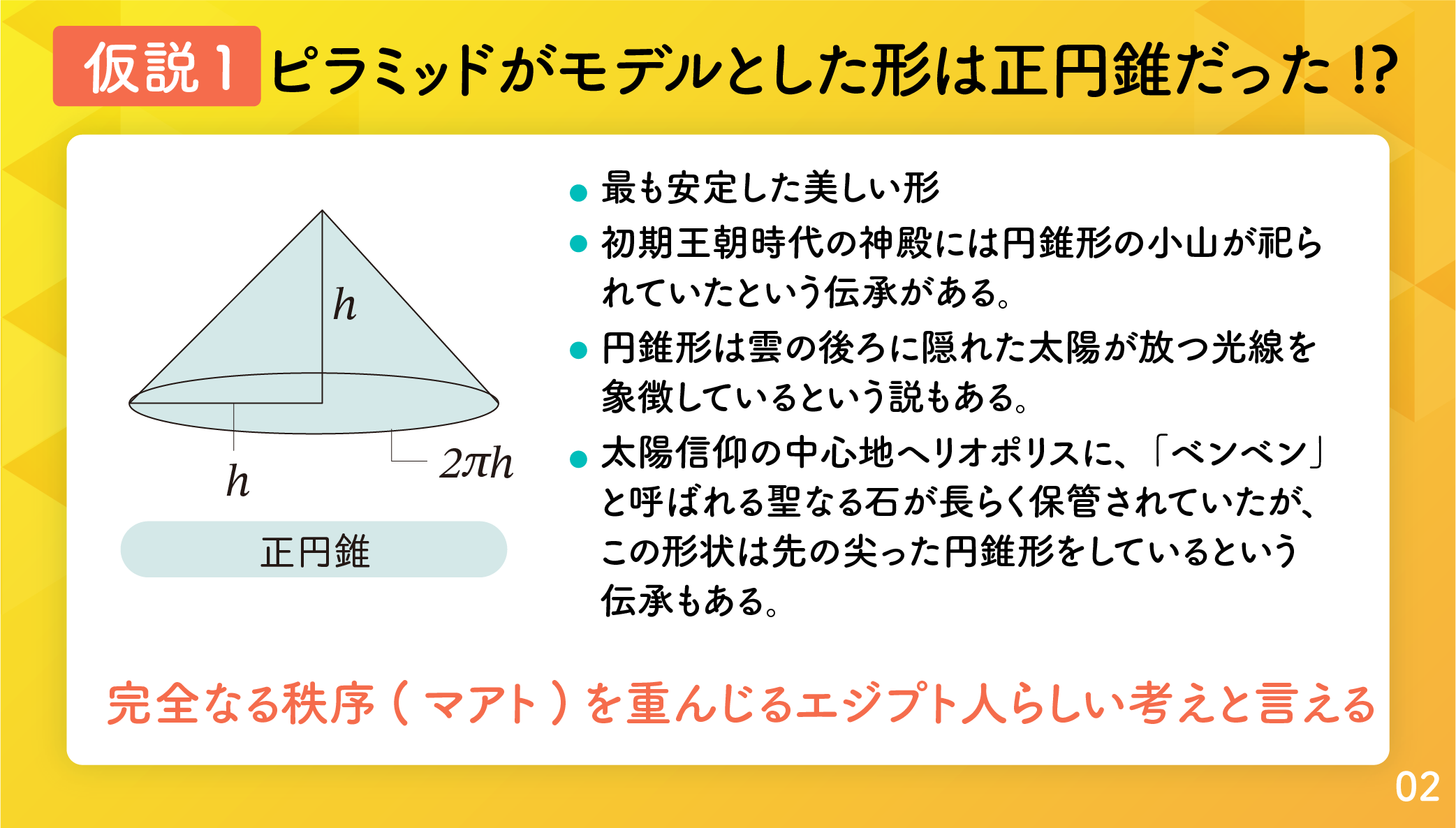
仮説1:ピラミッドのモデルは高さが底円の半径に等しい円錐形だった
円錐形で、最も安定した美しい形は、高さが底円の半径に等しい円錐形です。これを正円錐と呼ぶことにし、次の仮説を立てることにします。
仮説1 ピラミッドがモデルとした形は正円錐であった。
初期王朝時代の神殿には小石や砂で作られた円錐形の小山が祀られていたという伝承があります。日本でも「おむすび」のもともとの形は神様にお供えするためのもので「円錐形」であったといいますし、山は信仰の対象でした。エジプト人は「原初の丘※」が円錐形であったと思っていたのかもしれません。またある研究者は、円錐形は雲の後ろに隠れた太陽が放つ光線を象徴していると言っています。ではなぜ正円錐なのでしょうか。
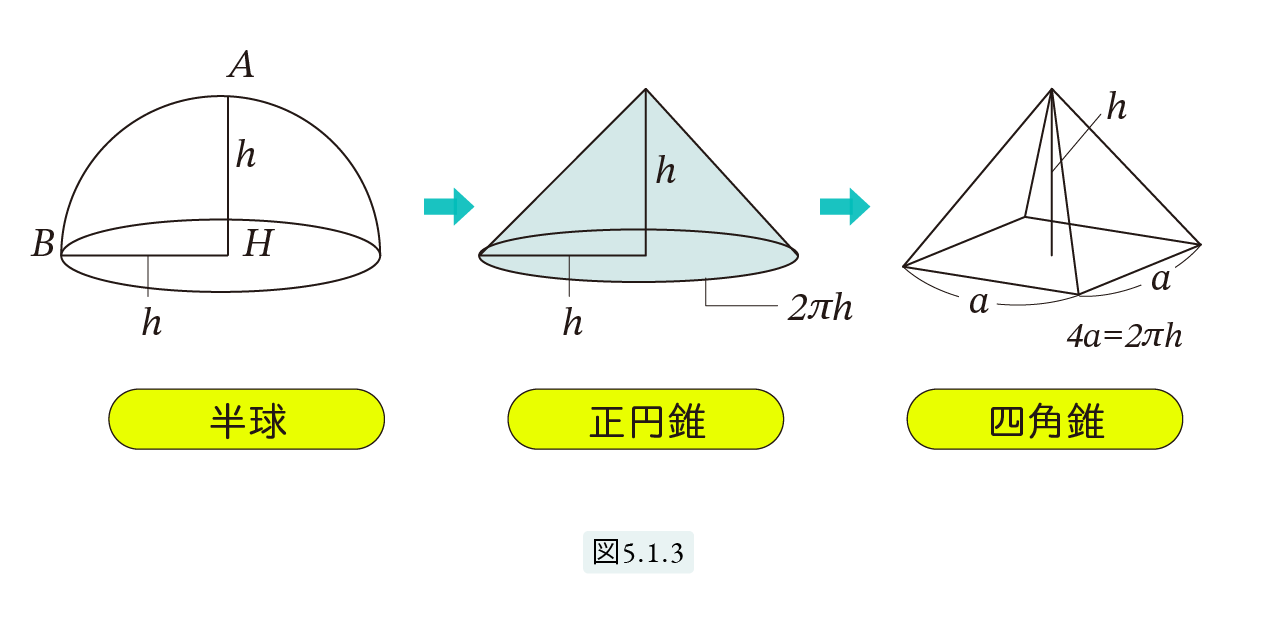
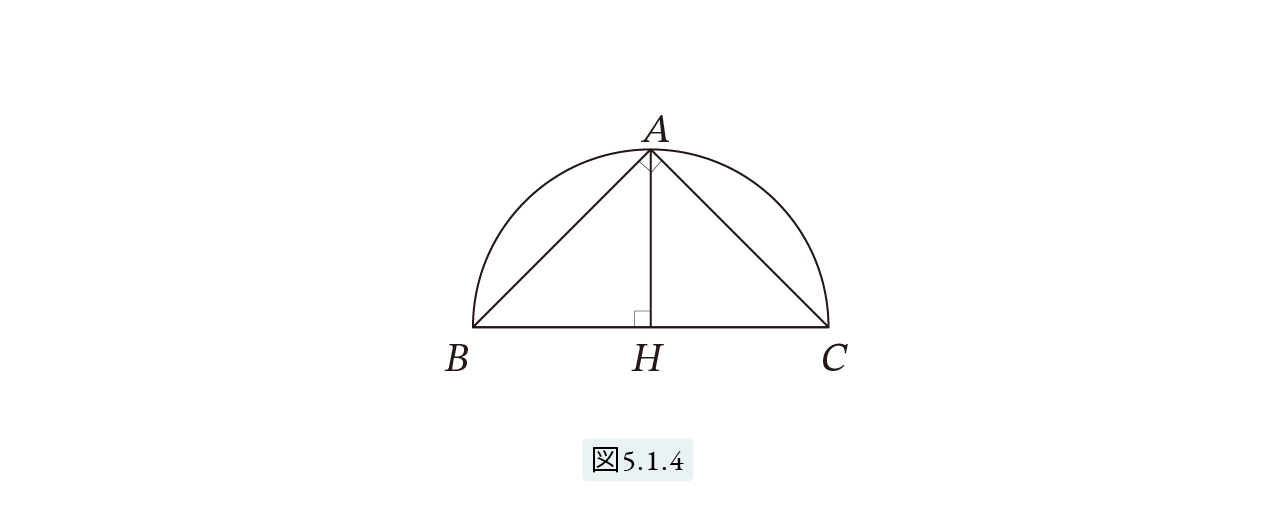
球を半分に割った半球を考えます図5.1.3。この半球の高さ AH は底面の円の半径 BH と等しくなります。エジプト人はこの半球を天球と見立てたのかもしれません。天頂 A を頂点とし、底面を底とする円錐は正円錐となります。また図5.1.4 のように正円錐の断面は美しい直角二等辺三角形が3つできます。
そもそも正方形とか円などは自然界には存在しません。こういった図形は人間の叡智の象徴です。日本でも京都の禅寺に、円と四角と三角 〇□△ が書かれた掛け軸が掛けてありました。また、日本の古墳も、前方後円墳、円墳、方墳などの形をしています。日本人もこういった記号に重要な意味が隠されていると考えたのかもしれません。しかし日本の古墳はすぐに木が生えて自然の中に溶け込み自然と一体化します。日本に神社や仏閣は自然の中に紛れるように建っています。日本人は自然と対立しようとは考えませんでした。
エジプトのピラミッドは、かつては真っ白な化粧石に覆われ白く輝いていたといいます。太陽神ラアはとても気まぐれで、時にはライオンに変身し人類を滅亡の淵に追い込んだこともあります。エジプト人がもっとも大切にしたのは完全なる秩序つまりマアトです。自然の本質は“混沌”であり、神々はときどき理不尽な洪水や旱魃を起こします。人々は、ホルスの化身である王は自然をコントロールする力があると信じていました。王は死んで北天の星となり、マアトが行きわたり、われわれ民衆が安心して暮らせるように守ってくれる、そのように願ってピラミッドを造ったものと思われます。
もちろん石材を使って円錐形の構造物を作るのは困難です。正円錐がどのようにしてクフ王の真正ピラミッドに型を変えたのか考えてみましょう。これにはエジプト人の幾何学的嗜好と美意識もあると思います。しかしもっと重要なことは、このピラミッドの建設によって、ファラオがこの自然界の摂理を支配していることを示したかったのではないでしょうか。したがって、ピラミッドが正確に東西南北を向いていること、底面が正確な正方形をしていること、底面の周長が高さを半径とする円周に等しいこと、などはこの完全なる秩序の象徴としてどうしても必要なことだったのだと思います。
仮説2:古代エジプト人は円の正方化問題を問いていた。
正円錐形をピラミッド型に忠実に置き換えるためには、底面の円を正方形に直さなければなりません。円を“等価な”正方形に変形する問題は、円の正方化問題と呼ばれ、面積に関する正方化と、長さに関する正方化の2つがあります。
円の正方化問題1 与えられた円に対し、その円と同じ面積を持つ正方形を作れ
円の正方化問題2 与えられた円に対し、その円と同じ長さの周を持つ正方形を作れ
円の正方化問題1は、ギリシアの有名な「3つの難問」の一つであり、数学史において重要な役割を演じ、多くの数学者がこの問題に挑戦しました。難問としてのこの問題は、定規とコンパスだけで作図をする問題のこと、つまり幾何学としての問題であって、数値として解くことではありません。数値として解くなら、エジプト人は、『3-3』で述べたように
直径 R の円の面積 ≒ 一辺が 8 9R の正方形の面積
として解いています。もちろんこれは近似値にすぎませんが。
ピラミッドの設計者は、正円錐の底面の円を周長の等しい正方形に変換しました。言い換えると、円の正方化問題2を解いていたのです。正確を期すためにこれを仮説2とします。
仮説2 エジプト人は直径 R の円周を 22 7 R で計算していた。
数学史を多少ともご存知の人は、この仮説2を聞くとびっくりするに違いありません。円周率の 22 7 は、『4-5』で述べたようにギリシアが誇る大数学者アルキメデス※が、精緻な理論と膨大な計算を駆使してやっと得た結果です。数学史に残る金字塔といってもいいでしょう。ですからこれまで誰もが、古代エジプト人が自力で円周率の 22 7あることを得たなどとは思いもよらなかったことでしょう。ですから、もし古代エジプト人がこの秘なる数 22 7を知っていたとするなら、ひとむかし前は数学の神トト神から、近代に入ってからは宇宙人かあるいは超古代文明から、この秘なる数を教えられたと考えても不思議ではありません。アルキメデスがあれだけ苦労をして得た 22 7 を、また円の正方化という重要な問題を、エジプト人はどのようにして得ることができたのでしょうか。答えはあっけないほど簡単です。
関連記事以下の記事で詳しく解説しています。
--Advertising--
円周の計測とエジプトの長さ単位
円周は円の面積より簡単です。私たちがたとえば丸太の周囲の長さを知りたいと思ったときどうしますか。断面の直径を測って計算するより、直接巻き尺などを巻きつけて測ればよいのです。さらに、エジプト人にとってとても幸運な偶然がありました。1腕尺= 7掌尺 という長さの単位です。これは人間の肘から指先までの長さが、手のひらの4本の指の幅と一致することから定められたもので、π とは何の関係もありません。
いま、直径が1腕尺の丸太が与えられたとしましょう。この丸太の1周は何掌尺 になるでしょうか。計算してみましょう。1腕尺 = 7掌尺 ですから
7 × π = 21.991… ≒ 22 掌尺
となります。腕尺 や 掌尺ではピンとこないかもしれませんから、cm で考えてみましょう。直径 7cm の円をコンパスで書いて、円周に沿って糸を置くなりして円周の長さを測ってみた、と思ってください。円周は 21.991 cm で、22cm との差はわずか 0.009 cm = 0.09 mm です。22 cm に対して誤差はたった 0.1mm となります。現在の私たちなら 0.1 mm を誤差と認識できますが、実際にはこの誤差は定規では測れません。ましてや古代のことなので、現在のような正確な定規もありません。直径 1腕尺 の円を描いてその周の長さを実際に測ったら「ぴったり22掌尺だ」と思ったに違いありません。これにはエジプトの長さが「10進法ではなかった」ことが幸いしました。10進法だと、たとえば、直径 10cm の円の円周は 31.4cm となり、30cm と見積もると端数が 1.4cm にもなってしまいます。言い換えると仮説2の根拠は、エジプトの「1掌尺=7腕尺」という単位系と、7π が 21.99 とほとんど整数値22 に近いという偶然にあります。
『1-1』で述べた「一輪車を使って測った説」について考えてみましょう。クフ王のピラミッドの底辺は「半径1腕尺 の車輪を70回回転させて測った」という説です。
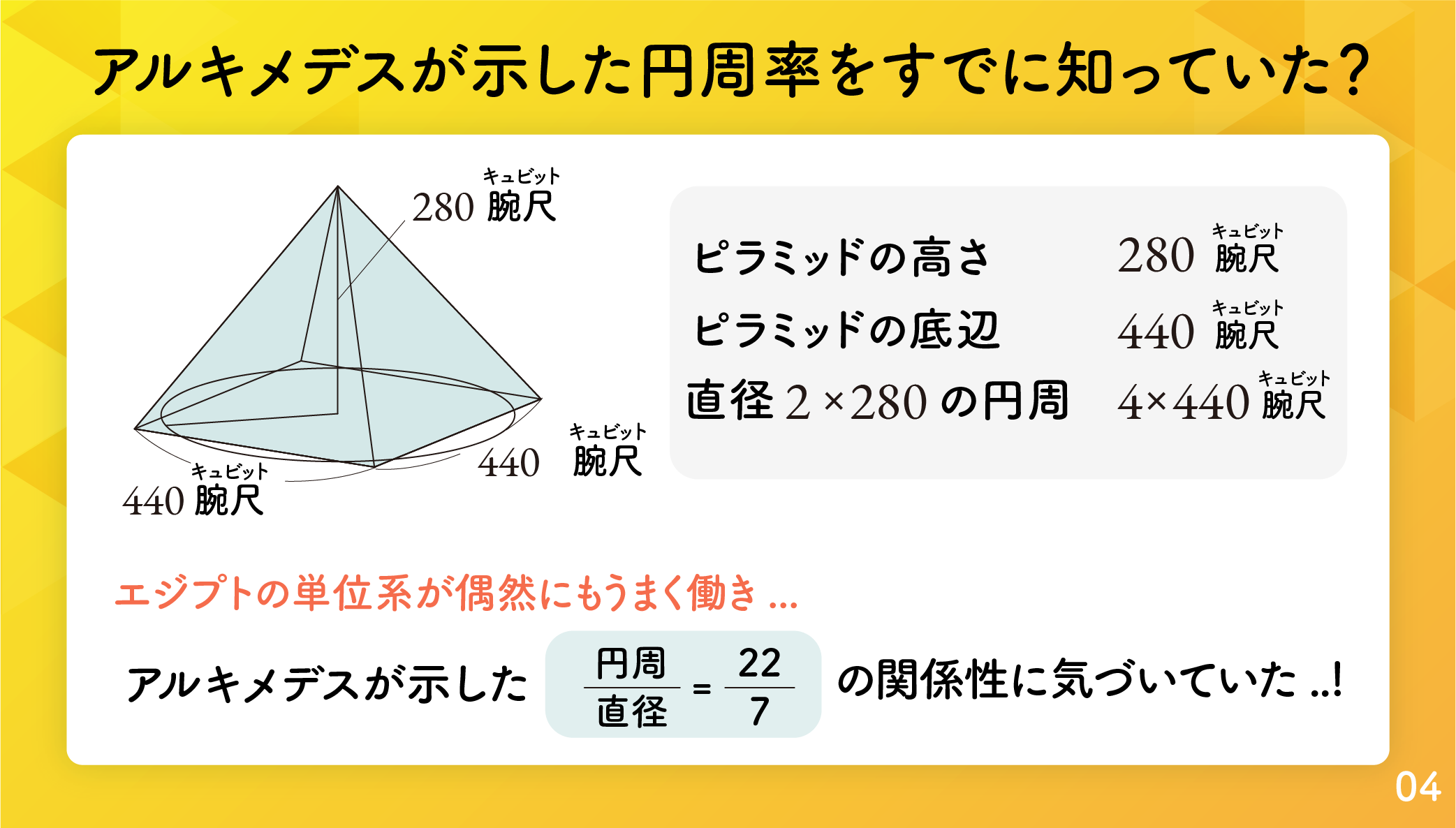
まず、エジプト人が円周率の謎を意識してピラミッドを建設したかどうかを検討しましょう。円周率の謎を考慮しなかったとしましょう。ピラミッドの底辺の計測に車輪を使うなら、高さが何であれ、セケドが何であれ、高さと底辺の比にπが入ってきます。たとえば、クフ王のピラミッドの底辺の場合、「なぜ車輪の回転数は70回なのですか」。60回でも50回でもいいはずです。さらに、表1に現れるピラミッドのほとんどのピラミッドのセケドが 5;1 2 か 5;1 4 のいずれかになることの理由が付きません。 では、円周率の謎を考慮してピラミッドを設計したとします。するとエジプト人は次が分かっていたことになります。
大ピラミッドの高さ= 280腕尺
大ピラミッドの底辺=440腕尺
直径 2×280腕尺の円周 = 4×440腕尺
エジプト人の数学の能力から判断して、このことからすぐに次に気が付くはずです。
円周 直径 = 22 7
これは仮説2にほかなりません。
上で、エジプト人が 22 7 に気づいたのは、1腕尺 = 7掌尺 というエジプトの単位が幸いしたと述べました。しかし、エジプト人はもっと賢かったかもしれません。『1-3』で、ピラミッド時代の腕尺 という単位は、「王家の腕尺 」と「標準腕尺 」の2種類があると述べました。なぜ2つの尺度があったのでしょう。正確には
王家の腕尺 = 52.375 cm,
標準腕尺 = 44.893 cm,
掌尺= 7.48cm
です。本書で使ってきた腕尺 は「王家の腕尺」です。なぜピラミッドの建設には標準腕尺 ではなく王家腕尺 を使ったのでしょうか。王家の腕尺 7 と標準腕尺 6を計算すると、
52.375 ÷ 7 = 7.48, 44.893 ÷ 6 = 7.48
となり、ともに 1 掌尺となります。つまり、「王家の腕尺」と「標準腕尺」の違いは単に 7 掌尺と 6 掌尺の違いだけで、「標準腕尺」を用いても何も問題はなかったはずです。「王家の腕尺」を用いたのは、円周を美しく表すため、
直径1腕尺の円周 = 22 掌尺という公式を成立させるためだったのではないでしょうか。
大ピラミッドが大切にした数
大ピラミッドが作り始められたのは第3王朝からです。第3王朝の王ジェセルの宰相であり、太陽神ラーの神官であったイムヘテプが神の啓示を受けピラミッドとそれを取り巻く祭殿を考案したとされています。後世の人々はイムヘテプのことを希代の大魔術師にして数学者、医学の父として敬い、やがて彼は神格化されていきます。ギリシア人がエジプトを支配するようになると、ギリシア人はイムヘテプをギリシア神話の医神アスクレピオスと同一視するようになります。イムヘテプが創ったのは真正ピラミッドの前の段階の階段ピラミッドですが、ピラミッドの基本設計はイムヘテプが作ったと、民間伝承や神話が伝えています。 この節のはじめで、「スネフェル王は3つのピラミッドを造ったが、最初の2つは角度が理想とする 52°ではなかったので作り直した」、と述べました。なぜ 52°なのかというと、「ヘリオポリスの神殿にあったベンベン石という秘宝、あるいは神殿に祀られていたという小石の円錐形の小山をモデルにしたのではないか」というのが歴史家の意見でした。エジプトでは円一周 360°という角度の単位は使っていません。角度はセケドを使います。52°はセケド 5;1 2 に当たります。実際のベンベン石とか小石の小山を測ったのでは、2度とか3度の違いは測定誤差で気になりません。つまり、セケド 5 でもいいはずです。スネフェル王は52°にこだわったのではなく、正確に言うと、セケド 5;1 2 にこだわったのです。なぜなら、セケド 5;1 2 は円周率の謎を満たすからです。