4-3.黄金比とは何か

黄金比とは

黄金比(外中比)とギリシアの幾何学

黄金比は、ギリシアの幾何学では外中比と呼ばれ、ギリシア「幾何学」のハイライトの一つです。黄金比のことをエジプト人が知っていたかどうかは疑問ですが、数学史では黄金比がよく出てくるのでここで説明しておきましょう。

ギリシアの「幾何学」は定規とコンパスだけで行うもので、数値は現れません。これは「禁止されている」というのではなく、そもそも前提となる概念のなかに数値が含まれていないのです。「幾何学」ではまず使ってもよい概念を公理や定義として述べてから理論を展開します。この方式はギリシア以降数学の標準として踏襲されてきます。ここでは、ギリシアの幾何学では比がどのように扱われているか、そのさわりだけをごく簡単に解説します。

「幾何学」では、長さ、面積、体積、角度を抽象的な対象として扱います。『4-2.ピタゴラスの定理』で述べたように、「2つの線分 α と β が等しい」とは α と β の長さが等しいことを、「2つの平面図形 α と β が等しい」とは α と β の面積が等しいことを意味します。体積や角度についても同様です。

a と b を線分とします。以下では、□( a, b ) は a と b を2辺とする長方形を表します。上で述べたように、線分 a といった場合、線分 a の長さを表すことがあります。同様に、□(a, b) は長方形を意味する場合と、その長方形の面積を表わす場合とがあります。

ギリシアの比の理論

合同と相似

ギリシア人は比の理論を、「自然数の比」と「量の比」の2つに分けて独立に構成しています。自然数は量ではないからです。本連載では「ギリシアの比の理論」について深くは解説しません(書籍の方で詳しく述べようと思います)。しかし現代の皆さんは、比 a : b、あるいは同じことですが、分数 a b のことをご存知だと思いますので、ギリシア人が比を図形的にどのように捉えていたかを説明するだけにします。

2つの図形 α と β が合同であるとは、α を移動すると β にぴったり一致するときのことを言います。したがって α と β が合同なら、α と β は等しいことになります。また、α を拡大あるいは縮小することによって β にぴったり重ね合わせることができるとき、 α と β は相似であるといいます。

皆さんは幾何の相似と合同についてはすでに知っているものと仮定します。以下では a, b, c, d は線分の長さを表すものとします。次の形の式を比例式 といいます。

a : b = c : d (1)

ここで、2つの辺の長さがそれぞれ　a と b ,　c と d の2つの長方形 □( a, b ) と □( c, d ) を考えましょう。

図4.3.2 のように2つの長方形を左下の角で重ねます。すると次が成立します。

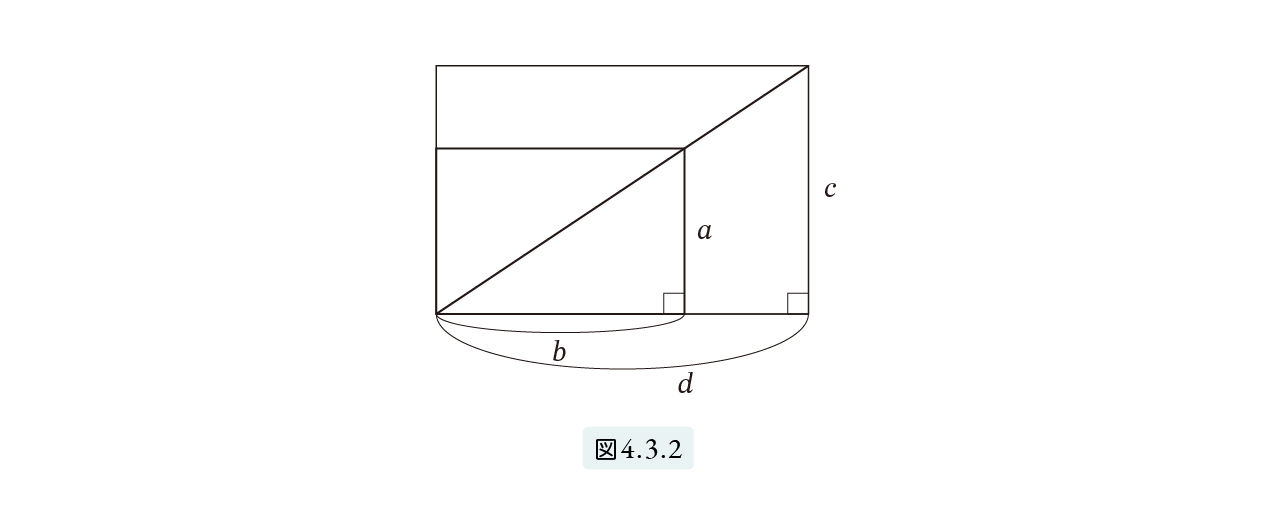
a : b = c : d　⇔ □( a , b ) と □( c , d ) は相似 　　(2)

ここで、「… ⇔ ～」は「… である必要十分条件は ～」と読みます。読者の皆さんは、(2) が比例式 a : b ＝ c : d の定義だと思ってください。つまり、a : b ＝ c : d とは、「a と b を2辺とする長方形を拡大または縮小すると c と d を2辺とする長方形にぴったりと重ねることができる」ことを意味します。

図4.3.2 のように2つの長方形を重ねます。すると、2つの長方形が相似である必要十分条件は、2つの対角線が重なることです。皆さんは、長方形の相似より図4.3.2の中の直角三角形の相似のほうが慣れているかもしれません。また、公式 (2) より次の公式の方をご存知かもしれません。

a : b = c : d　⇔ □( a , d ) ＝ □( b , c ) (3)

公式 (3) は、外項の積は内項の積に等しいと読みます。 (3) を証明しましょう。a : b ＝ c : d とします。すると □( a , b ) と □( c , d ) は相似です。したがって、2つの対角線は重なります。図4.3.3より、三角形 (イ) と (イ’) は合同、三角形 (ロ) と (ロ’) も合同となります。同様に大きい三角形 (イロハ) と (イ’ロ’ハ’) は合同ですから、2つの長方形 (ハ) と (ハ’) は同じ面積となります。よって次が成立します。

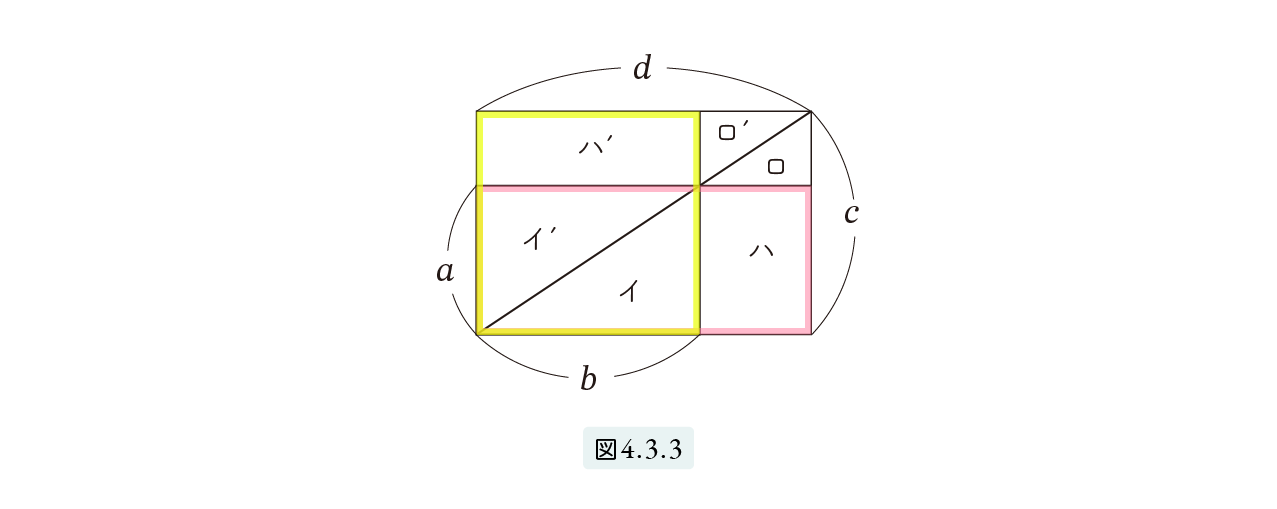
□( a, d ) ＝ (イ)＋(イ’)＋(ハ) ＝ (イ)＋(イ’)＋(ハ’) ＝ □ ( b, c )

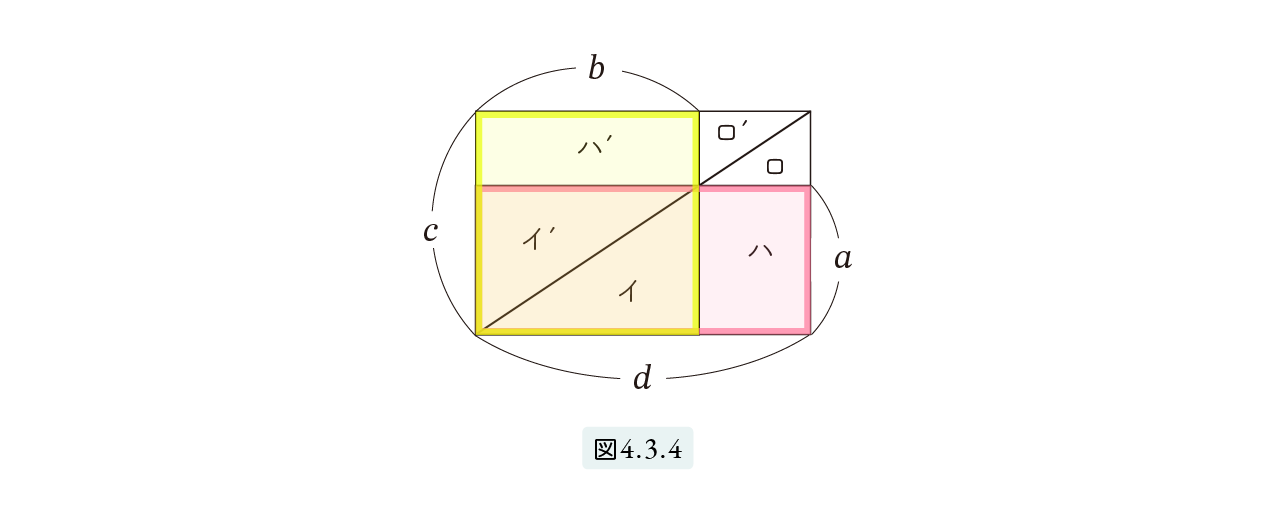
逆に、□( a, d ) ＝ □( b, c ) が成立したとします。図4.3.4参照。 (イ)＋(イ’) は2つの長方形の共通部分ですから (ハ) ＝ (ハ’) となります。したがって、(イ’)＋(ロ’)＋(ハ’) は大きい長方形 □(c, d) の半分の三角形となります。よって、□( a, b )の対角線は □(c, d) の対角線と重なり、□( a, b ) と □( c, d ) は相似となります。

黄金分割・黄金率・黄金比

黄金分割とは、線分 AB を点 C で次を満たすように分割する分割の仕方のことをいいます。

短い方 : 長い方 ＝ 長い方 : 全体 　　(4)

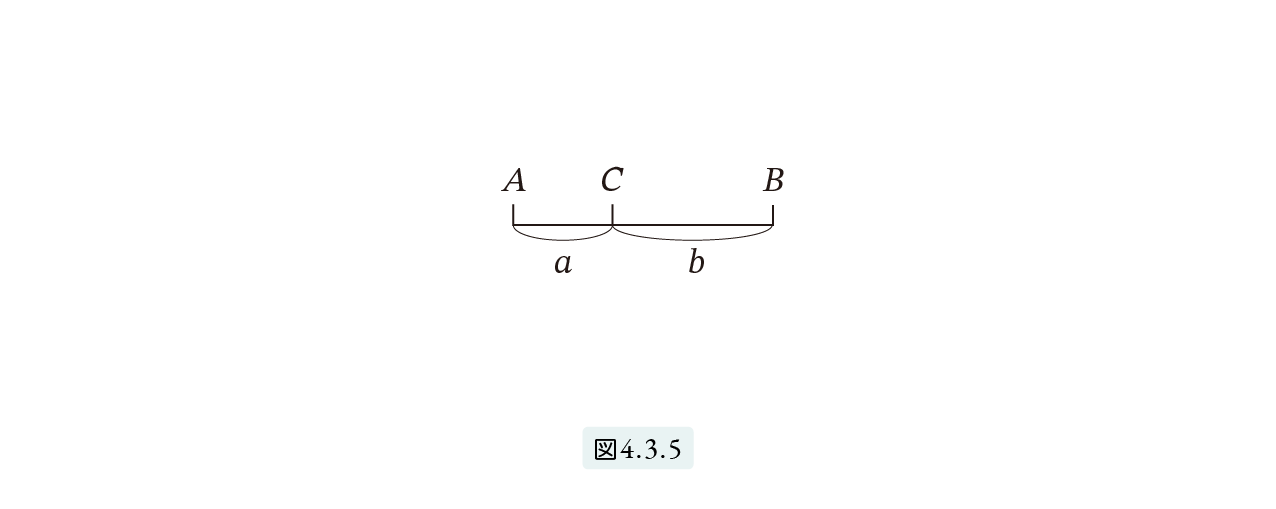
AC ＝ a , CB ＝ b とし、a ＜ b とします。すると、(4) は次のように表されます。

a : b = b : a + b 　　　 　　　　 　(5)

外項内項の規則 (3) より、次が成立します。

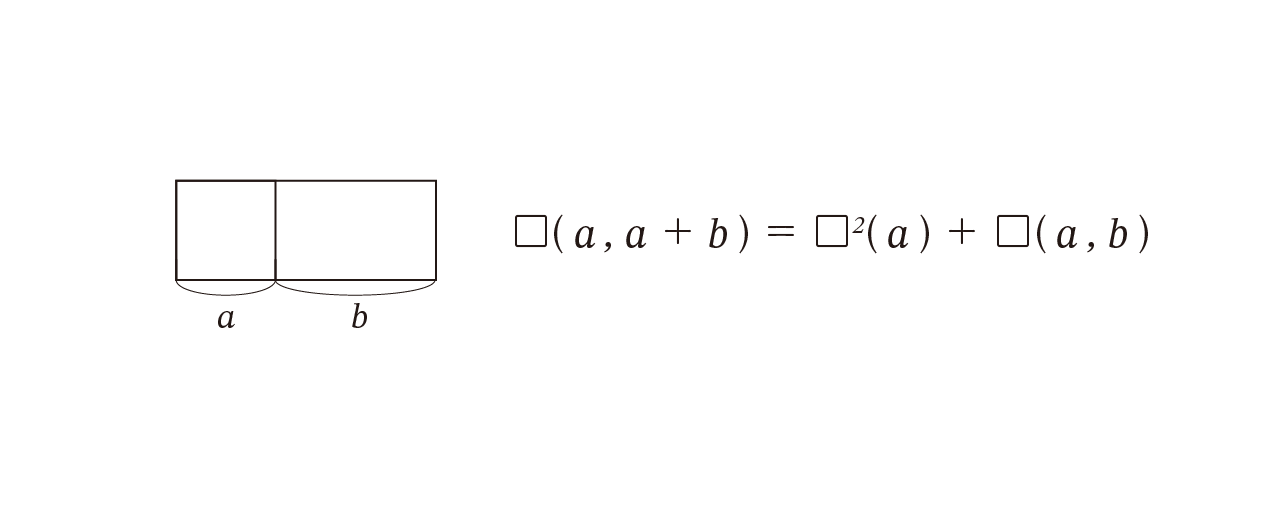
□² ( a ) ＋ □( a, b ) = □² ( b ) 　　 　　 (6)

式 (6) では、 a ＋ b は線分 a に線分 b をつないでできる線分を意味します。(6) は「辺 a 上の正方形と a と b を2辺とする長方形の和は b 上の正方形に等しい」を意味します。

ここまでがギリシアの幾何学のお話で、ここからは現代数学を使って黄金分割の説明をします。したがって、以下では a, b, c, d は正の実数とします。

(6) を満たす比 a : b を黄金比といい、b a を黄金率といいます。b a の逆数 a b を黄金率と呼ぶこともあります。本連載では、b a を黄金率としています。(6) の両辺を a² で割ると、

1+ b a = (b a)²

となります。b a ＝ x と置いて整理すると、

x² = x + 1 　　(7)

という2次方程式が得られます。この方程式の正の解は

φ = 1+$\sqrt{5}$ 2 = 1.618033989

となります。この φ が黄金率で、比 1 : φ が黄金比です。

黄金率の不思議

古代には方程式などはありませんし、$\sqrt{5}$ などといった数の表し方も知りません。したがって読者の皆さんも方程式 (7) を解く必要はありません。皆さんは a² を電卓で計算して実際に (7) が成り立つことを確かめてください。ついでに 1 φ も計算してみてください。

φ ＝ 1.61803399
φ² ＝ 2.61803399
1 φ ＝ 0.6180339887

不思議なことに気がつきませんか。この3つの値は小数点以下が一致するのです。φ は (7) の解だから φ² ＝ φ＋1 が成立します。両辺をφで割って整理すると、

1 φ = 　φ ー 1

となります。つまり、黄金率 φ は、1を加えると平方となり、1を引くと逆数になるのです。黄金率が不思議な現象を起こすのはこのようなところに原因があるのかもしれません。

黄金長方形と再帰構造

1 : φ の両項にφを掛けて、1 : φ が黄金比であることを確かめてください。図4.3.6

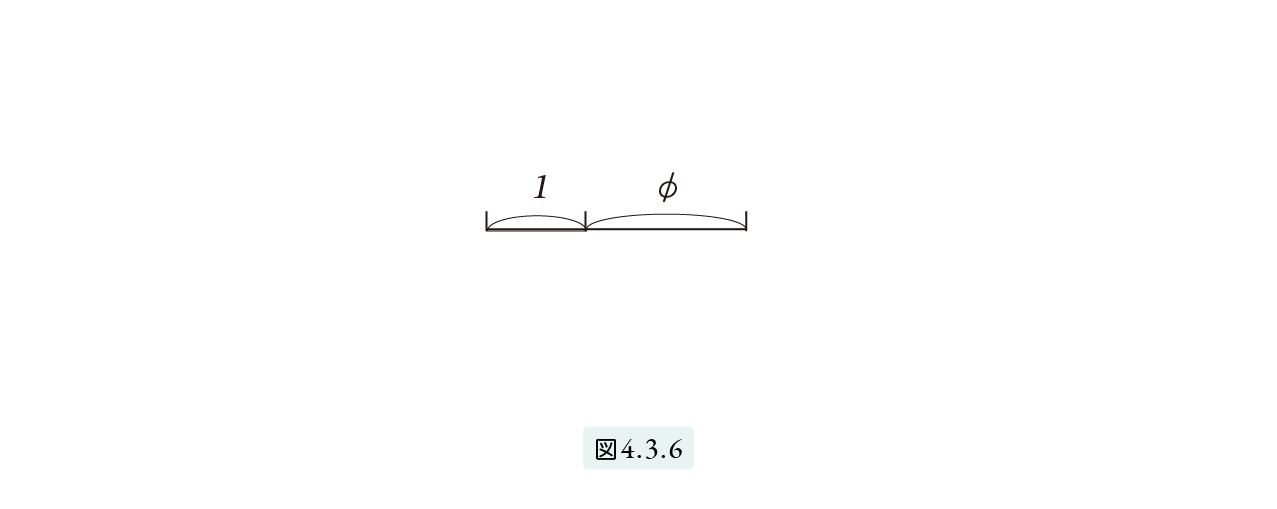
1 : φ = φ : φ² = φ : 1 + φ

a : b を黄金比とします。つまり次を満たすとします。

a : b = b : a + b 　　(8)

辺の比 a : b が黄金比である長方形を黄金長方形といいます。図4.3.7 の左上の a × b の長方形を黄金長方形とします。

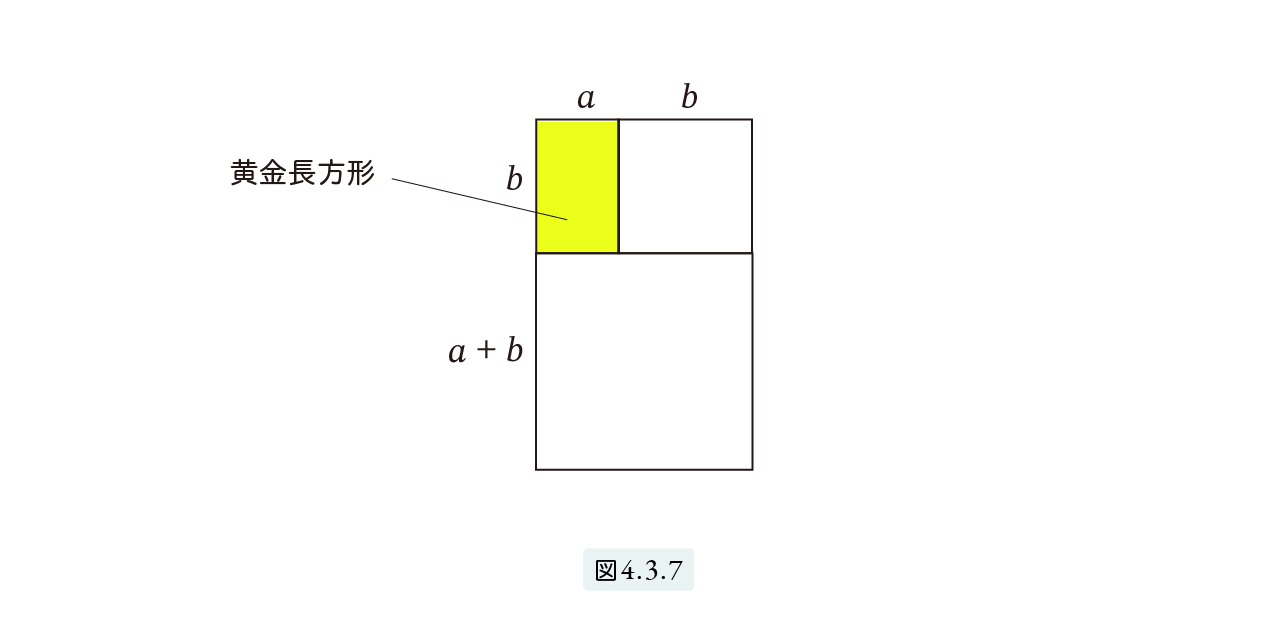
この長方形の右に b × b の正方形をくっつけましょう。すると (8) より、新しくできた長方形 b × ( a + b ) もまた黄金長方形となります。この黄金長方形の下にさらに ( a + b ) × ( a + b ) を付け加えることができます。この操作は無限に続けることができます。こういった構造を再帰構造といいます。

黄金比とフィボナッチ数列

さて、φ の近似値として 1.6 を取ったとします。すると、

1 : 1.6 ＝ 10 : 16 ＝ 5 : 8 　　(9)

となります。この 5 : 8 をよく黄金比（の近似値）として用います。5 : 8 よりもよい黄金比を使いたいときは、図4.3.7 の大きい長方形を用います。すなわち a＝5, b＝8 として、

b : a ＋ b ＝ 8 : 13 　　 　　 (10)

を使います。実際 a + b b を計算してみると、

13 8 ＝ 1.625

となり、1.6 よりも φ に近づきます。逆に図4.3.7 で大きな長方形から小さい長方形に戻ってみましょう。すなわち、a ＋ b＝8 , b ＝ 5 から a, b を求めると、

a : b ＝ 3 : 5 　 (11)

が得られます。

皆さんはフィボナッチ数列をご存知ですか。次がフィボナッチ数列です。

1, 2, 3, 5, 8, 13, 21, …

最初から、1と2を足すと3が得られ、2と3を足すと5が得られ、3と5を足すと8が得られ、… と続きます。上で出てきた式 (11), (9), (10) の比を見てください。3 : 5, 5 : 8, 8 : 13 はこのフィボナッチ数列のなかに順番に現れています。つまり、フィボナッチ数列の隣り合った数の比は黄金比の近似値となっているのです。右に進むほどより正確な黄金比となります。

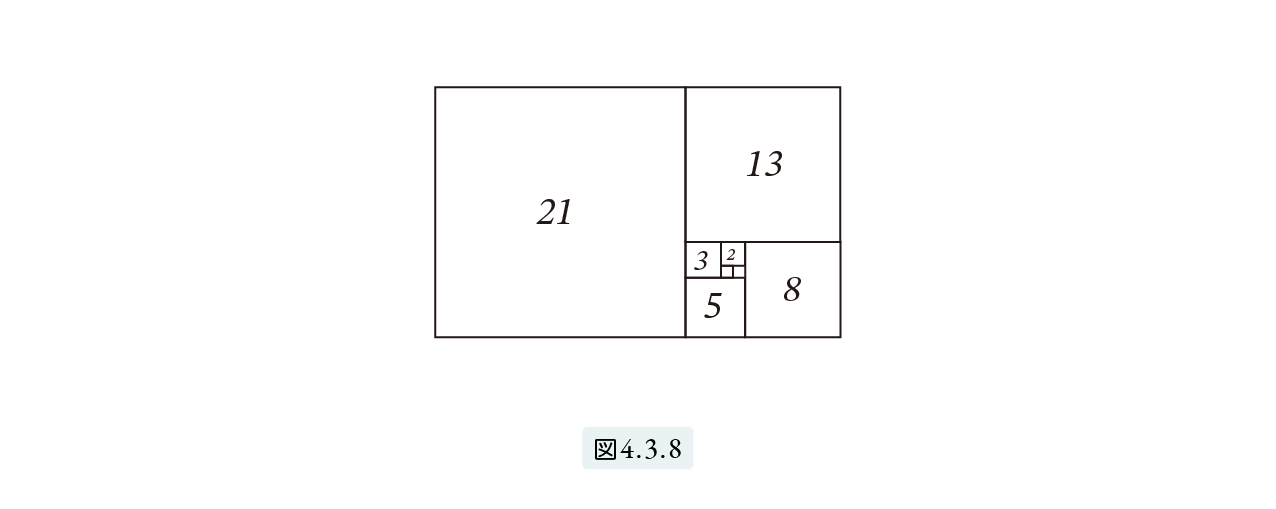
ここでフィボナッチ数列の話を終え、話題を変えると読者のなかには「フィボナッチ数列の話はどうなったのだ。この話の目的は何だったのだ」と不満の声を上げる人がいるように思います。「数学は何を目標にしているかわからないから嫌いだ」という意見もよく聞きます。フィボナッチ数列と黄金比は、円周率 π と同様、思わぬところでよく顔を出します。フィボナッチ数列が自然現象によく現れるのは図4.3.8 のような繰り返し構造に関係があるようです。また、黄金比の定義 (4) は図形的には図 4.3.7 の2つの長方形の相似で示され、これが図 4.3.8 の再帰構造を生み出す元となっています。ピラミッドとの関連では、次の比『3 : 5 』 と 『5 : 8 』が後の議論で出てきますから覚えておいてください。

古代ギリシア幾何学と五芒星

前にも述べましたが、$\sqrt{5}$ とか φ のような無理数は古代には存在しません。これらが数として扱われるようになったのはやっと近世に入ってからです。バビロニア人もアルキメデスも $\sqrt{2}$ とか $\sqrt{3}$ の“近似値”を計算していますが、まだ $\sqrt{2}$ や $\sqrt{3}$ そのものを数として扱ってはいません。黄金比という言葉も最近（1930年代ごろ）できた言葉で、ルネサンス期にはなかったようです。ギリシアの幾何学では外中比と呼ばれていましたが、本連載では黄金比という言葉で通します。

φ＝1.618… という数値が使えないとしたら、黄金比はどのように扱われていたのでしょうか。ギリシア幾何学によく出てくる五芒星を例として説明しましょう。図4.3.9 の星形を五芒星といいます。各頂点を結ぶと図4.3.10のような正五角形となります。

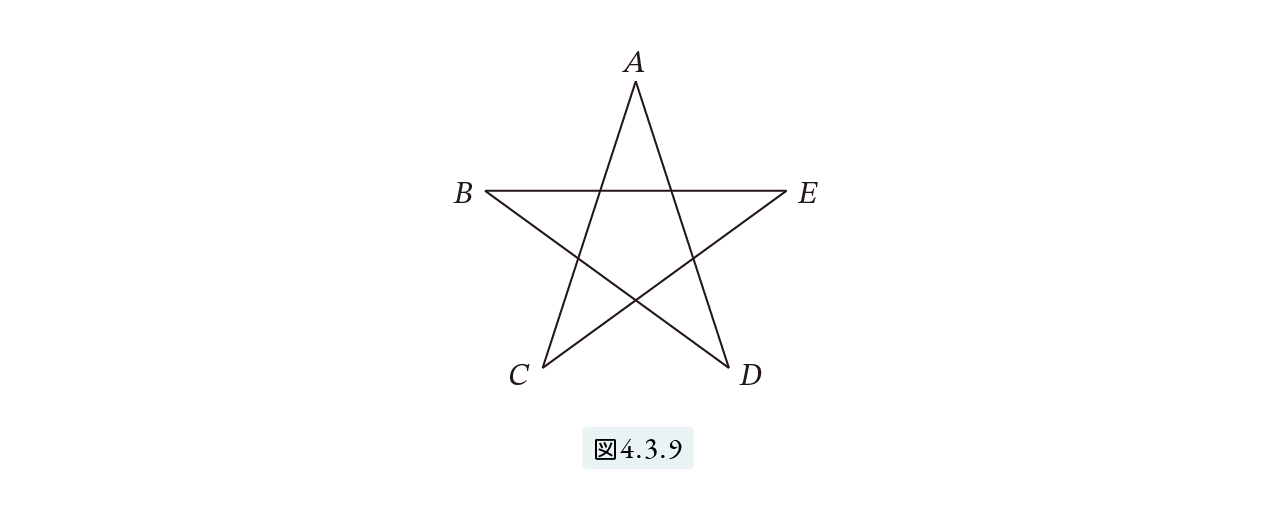
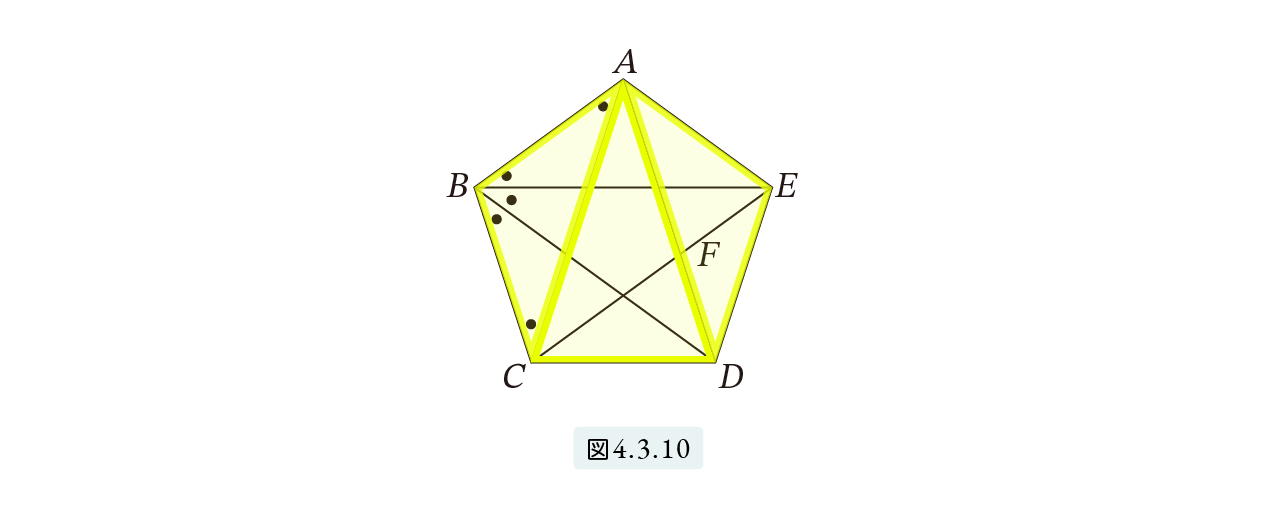
五芒星の作図が、黄金比の研究のおもな動機だといわれています。ここでは CD ： AC が黄金比となることを証明しましょう。CD は正五角形の1辺、AC は正五角形の対角線です。したがって

1辺 : 対角線 ＝ 黄金比

と書くと覚えやすいでしょう。

ギリシア人は角度も数値として扱っていませんでした。円一周 360度としたのはバビロニア人です。ここでは角度を使って証明しましょう。

正五角形は、3つの三角形 ABC, ACD, ADE に分けられます。内角の和は 180 × 3＝540度ですから、1つの内角は 540 ÷ 5＝108　度となります。三角形 ABC は二等辺三角形で ∠B は 108度だから、底角の一つは ( 180 – 108 ) ÷ 2 ＝ 36　度です。三角形 ABC と BCD は合同だから、∠CBD も36度となります。黒点・ひとつ 36度とすると、図4.3.10 で示されるようになります。

ここで三角形 ACD に注目しましょう。三角形 ACD は黄金三角形と呼ばれることがあります。ここで、F は AD と CE の交点です。図4.3.11 参照。

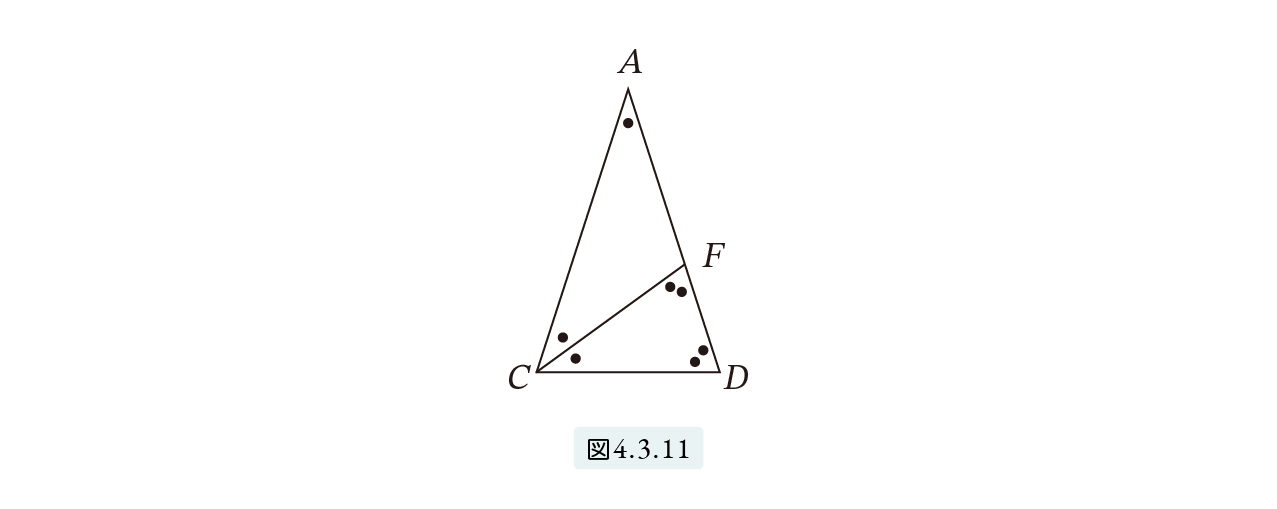
三角形 ACD と三角形 CDF 共に二等辺三角形で、互いに相似です。したがって、

AC ＝ AD, AF ＝ FC ＝ CD
FD : CD ＝ CD : AC

が得られます。この2つの式より次が得られます。

FD : FA ＝ FD : CD ＝ CD : AC ＝ FA : AD

最初と最後を取り出すと、「短い辺FD：長い辺FA ＝ 長い辺FA : 全体 AD」となり FD : FA は黄金比となります。したがって、この式の途中にあらわれる CD : AC も黄金比です。

黄金分割の作図法

エジプト人は黄金分割を知っていたのでしょうか。与えられた線分 A をロープを使って黄金分割する方法を述べましょう。点 A を通る AB に垂直な直線を引き、その線分上に点 D を、DA ＝ 1 2 AB となるようにとります。線分 DB上に点 E を DE ＝ DA となるように取ります。AB上に点 C を CB＝EB となるように取ります。すると、点 C は線分 AB を黄金分割します。図4.3.12。

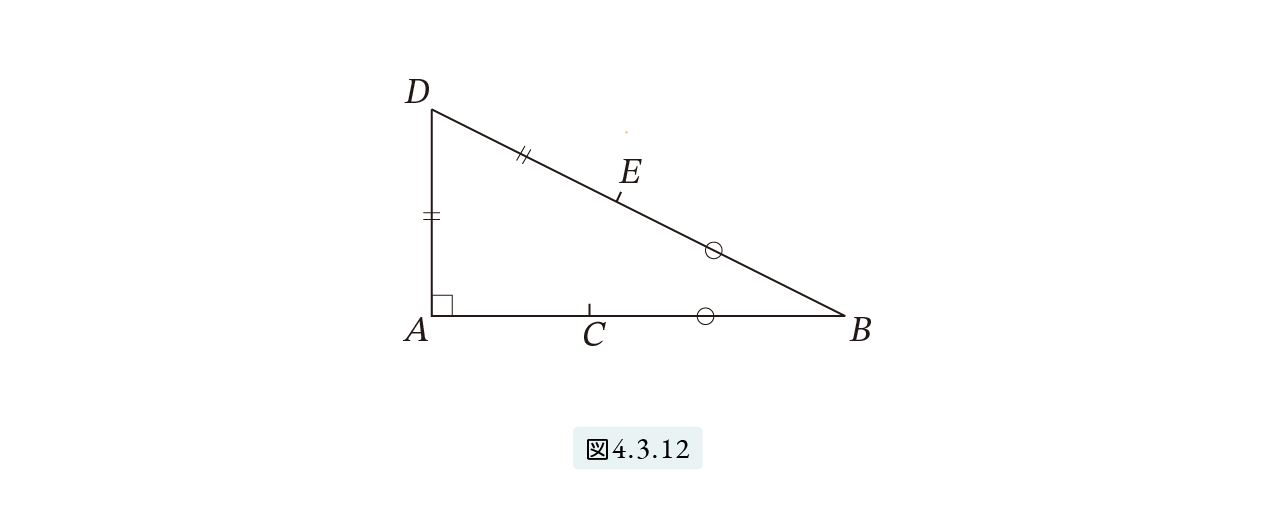
このような方法なら、杭とロープだけを使って AB を黄金分割することができます。やり方さえ覚えれば実行は簡単です。ですがエジプト人は本当にこんな方法で黄金分割をしたのでしょうか。現代の数学を使って、点 C が AB の黄金分割であることを証明しましょう。この計算は、ピタゴラスの定理と高校生程度の計算を必要としますが、単なる計算問題で論理的な難しさはありません。

AB ＝ 2, DA ＝ 1 としても一般性を失いません。すると、DB= $\sqrt{1+2^2}$ = $\sqrt{5}$ ですから

AC : CB = 2 – ($\sqrt{5}$ – 1) : $\sqrt{5}$-1
= (3 – $\sqrt{5}$) : ($\sqrt{5}$-1)
= (3-$\sqrt{5}$)(3+$\sqrt{5}$) : ($\sqrt{5}$-1)(3+$\sqrt{5}$)
= 4 : 2$\sqrt{5}$+2
= 1 : (1+$\sqrt{5}$)/2 = 1 : φ

となり、C はAB の黄金分割となっています。

ギリシア人もこれと同様な方法で黄金分割を行っています。もちろんギリシア人の方法とその証明は上のような数値を使ったものではなく、複雑で精緻な「幾何学」を使ったものでした。上で述べた「ロープを使った黄金分割の仕方」は、後世の創作だと思います。この黄金分割の作図はロープ１本あればできるのでエジプト人も知っていたはずだという人がいます。もしエジプト人がこの方法を使ったと主張するなら、「どのようにしてこの方法を思いついたのか」ということと「なぜ黄金分割が必要だったのか」を明らかにする必要があります。古代の数学史の記述、特にギリシアの数学にも、このような後世の創作がたくさん混じっているようです。この根底には「数学は普遍的事実を述べるもの」であるからどのような述べ方をしてもかまわない、という考えがあったからだと思います。