ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
5-6.エラトステネスの地球の測量
ページ目次
歴史の偉人伝と教科書:事実と創作の狭間
現在ではあまり流行らないようですが、昔は「偉人伝」とか「英雄伝」がよく書かれ、読まれていました。偉人は非の打ち所がない立派な人で、英雄は勇敢無敵でその上美男子でした。そういった話では、面白ければ面白いほど史実から離れていくような気がします。あたかも著者がその場にいたような臨場感のある描写や、録音機もない時代なのに長々と繰り返される会話などは、史実というよりは歴史小説です。しかしこういう要素がないと、現在の歴史の教科書とか数学史のようになってしまい、あまり一般受けしないのかもしれません。古代の「伝記」は、読者に受けるように書かれたものでした。それに、現在の著作のように何千部も印刷される公的なものではなく、いたって私的なものでした。ですから、著者は著作に対して責任をとる必要もなく、かってに創作したり事実を変えたりすることがよくあったようです。以下で述べるエラトステネス※についても、そのような伝記から採ったものです。
エラトステネス:多才さと業績
エラトステネスは、ヘレニズム期を代表するギリシアの科学者としてとても有名で、後の著作にたびたび出てきます。エラトステネスは、アレクサンドリアの西方、現在のリビアにあるキュレネに生まれ、しばらくの間学園都市アテナイで学んだ後、紀元前244年ごろに、プトレマイオス王朝の王子の家庭教師として招かれ、アレクサンドリアにやってきました。前236年には、大図書館の館長に就任し、終生をアレクサンドリアで過ごしたということです。
エラトステネスに関しては、とても多くの逸話や業績が伝えられています。詩人、音楽家、文学の批評家など多才で、喜劇の著作まであります。数学や天文学に関する業績も多数あります。しかしこれらが書かれたのはローマ時代で、ギリシア人はもはやエジプトの支配者ではなく、ギリシア科学は存亡の危機にありました。当時のムセイオンとよばれる科学研究所はローマ皇帝の援助で成り立っていました。ギリシアの科学を宣伝するためにはある程度の粉飾も仕方がありません。
エラトステネスはアルキメデス※から手紙をもらっており、当時でも一流の学者と認められていたようです。しかしあまりにも多くの分野に手を染めたため、どれか一つに抜きんでていたというわけではなさそうです。同時代の学者からは、ギリシアのアルファベットの最初の文字アルファではなく、2番目の文字をしめすベータと呼ばれていたようです。つまり、どの分野でも第一人者ではなく二番手だったということです。数学史の専門家の中には「エラトステネスは大図書館に所蔵されていた文書のほとんどに目を通し、大変な博識ではあったが、自分の業績は何もなかった」という人もいます。
エラトステネスは、エラトステネスのふるいとして有名な素数をいちどにたくさん求めるアルゴリズムの発明者としても有名です。読者の皆さんは素数などに興味がない方が多いかもしれません。数学の専門家でもないかぎり、素数に興味を持つ人は「数学好き」、いまの言葉でいうと「数学オタク」なのかもしれません。しかし以下の事項は、ゆっくりと読めばごく簡単です。
エラトステネスのふるい
自然数 a が2つの自然数 b と c の積で表されたとします。すなわち
a = b × c
このとき、a は b の倍数、b は a の約数であるといいます。たとえば 12 は次の6個の約数
1, 2, 3, 4, 6, 12
を持ちます。1 と 12 も 12 の約数であることに注意してください( 12 = 1 × 12 )。素数とは 1 と自分自身以外に約数を持たない自然数のことです。例外として1 は素数ではないとします。エラトステネスは、いっぺんにたくさんの素数を計算する方法を見つけました。これを現在ではエラトステネスのふるいと呼んでいます。
50以下の素数をすべて求めるものとします。表5.5.1 のように、1から 50 までの数を書きます。1 から順に素数でないものを消していきます。1 は素数でないから消します。表では、消したものは赤で示します。1の次は 2 です。消されていない素数に出会ったら、その数は素数です。2は消されていないので素数です。素数は 〇 で囲みます。次に、2の倍数をすべて消します(4, 6, 8, … 50)。これらは2を約数として持つので素数ではありません。 次に進むと3に出会います。これを 〇 で囲み、3 の倍数をすべて消します。表では緑で示してあります。
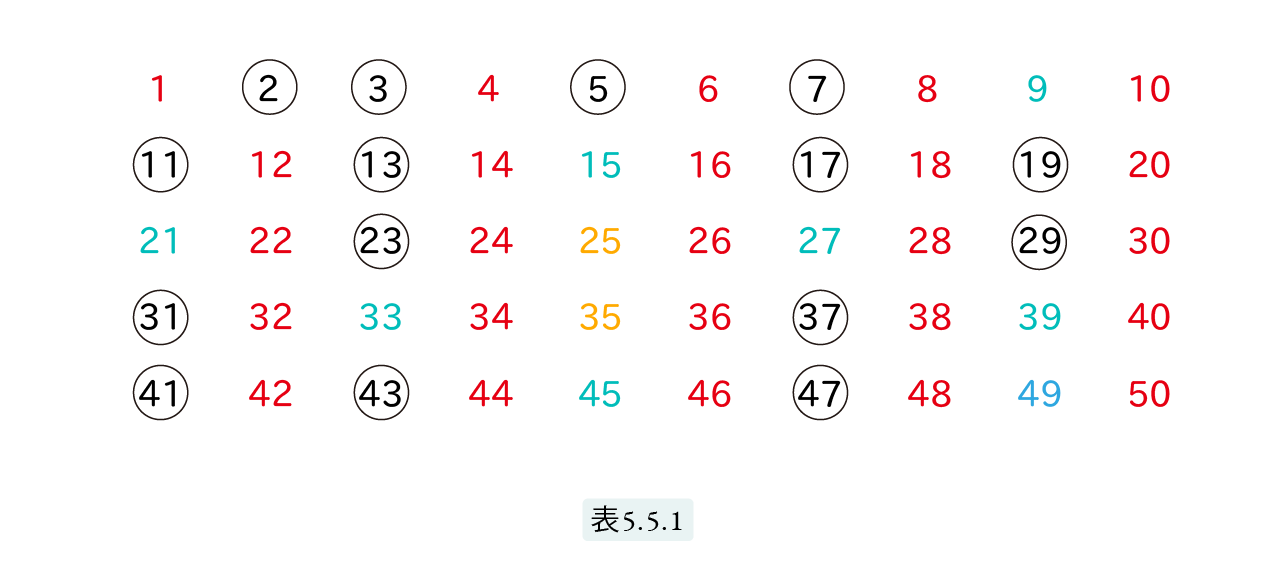
この操作を続けると、次が消されずに残ります。
2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 ,
読者の皆さんはこれをどのように感じますか。言われてみればなるほどと思うかもしれませんが、感動するようなものでもありません。これはギリシア数学特有の論証ではなく、手続つまりアルゴリズムです。単に素数を見つけるだけで、素数に対する何らかの性質が明らかになったわけでもありません。素数は近世に入ってから数学者の注意を引き、数論という分野を作るもとになりましたが、素数の研究は純粋に理論のためだけのもので、なんの役にも立たないと思われていました。素数が大勢の人の注目を集めるようになったのは、20世紀に入ってコンピュータが発達したおかげです。現代ではコンピュータのセキュリティの保護のために素数はなくてはならないものになっています。エラトステネスのふるいは、大きな素数表を必要とする素数の研究者にとっては貴重なものでした。しかしヘレニズム時代に、いったい何人の人が素数に興味を持っていたでしょう。読者の皆さんはエラトステネスのふるいを読んで“おもしろい”と思いましたか? エラトステネスは何の目的でこのアルゴリズムを考えたのでしょうか? これはエラトステネスの発明ではなく、素数の研究が盛んになった後世の誰かがこのアルゴリズムにエラトステネスの名前を割り当てただけのように思われます。
エラトステネスと地球の周長
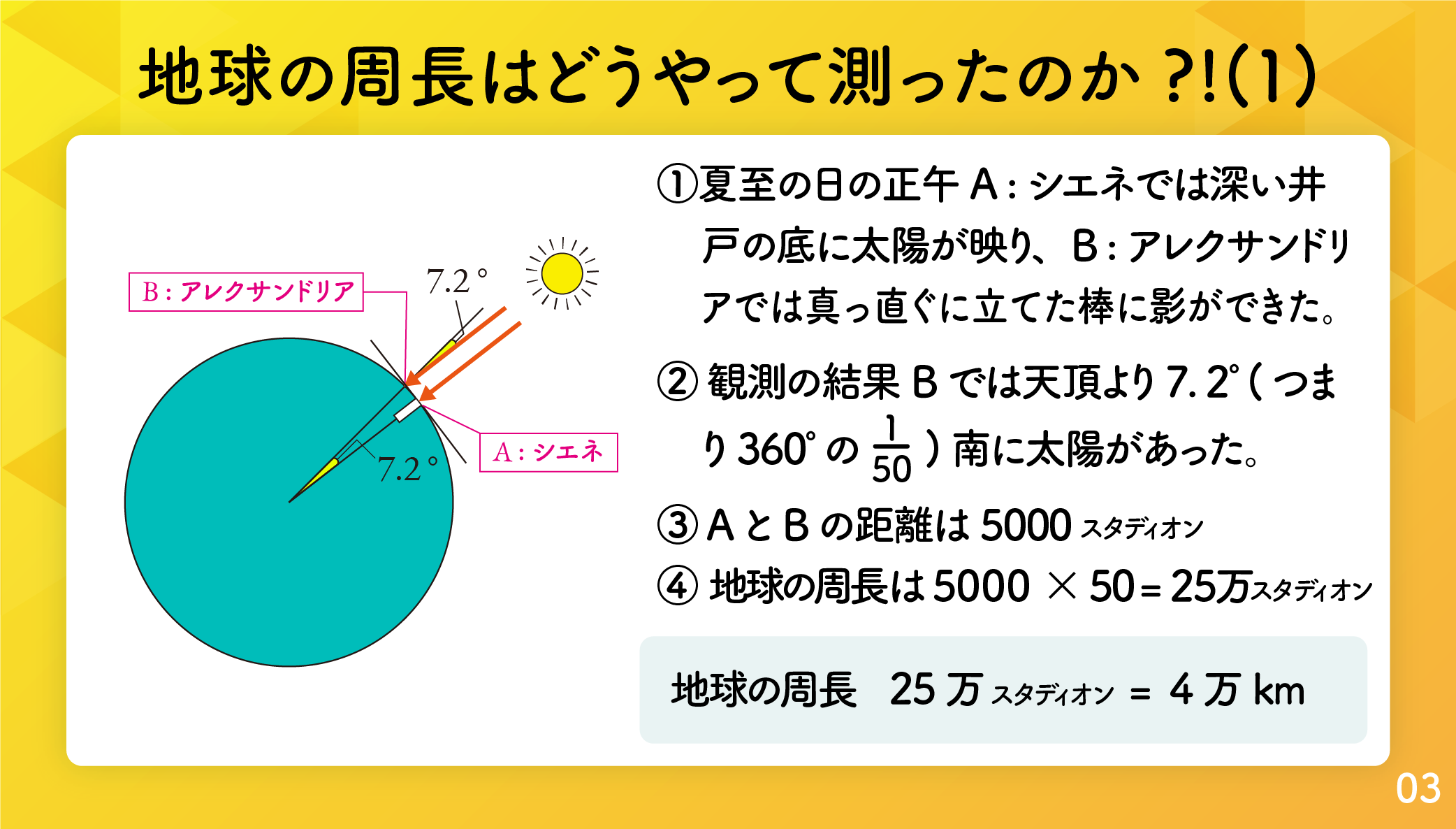
さて地球の測量のお話に戻りましょう。大図書館の図書館長であるエラトステネスは、ある日エジプトの年中行事の書かれたパピルスを読んでいて、アレクサンドリア市の南にあるシェネという町で、あるお祭りの日に深い井戸の底に太陽が映ることを知りました。あるお祭りの日とは夏至の日のことで、エジプトでは夏至の日にはお祭りがありました。エラトステネスは同じ夏至の日の正午、アレクサンドリアで真っすぐに立てた棒の影の長さを測りました。その影の長さから、棒と太陽光線がなす角は 7度12分でした。図5.5.2 で A はシェネ、B はアレクサンドリアで、 7度12分 = 7.2度 です。
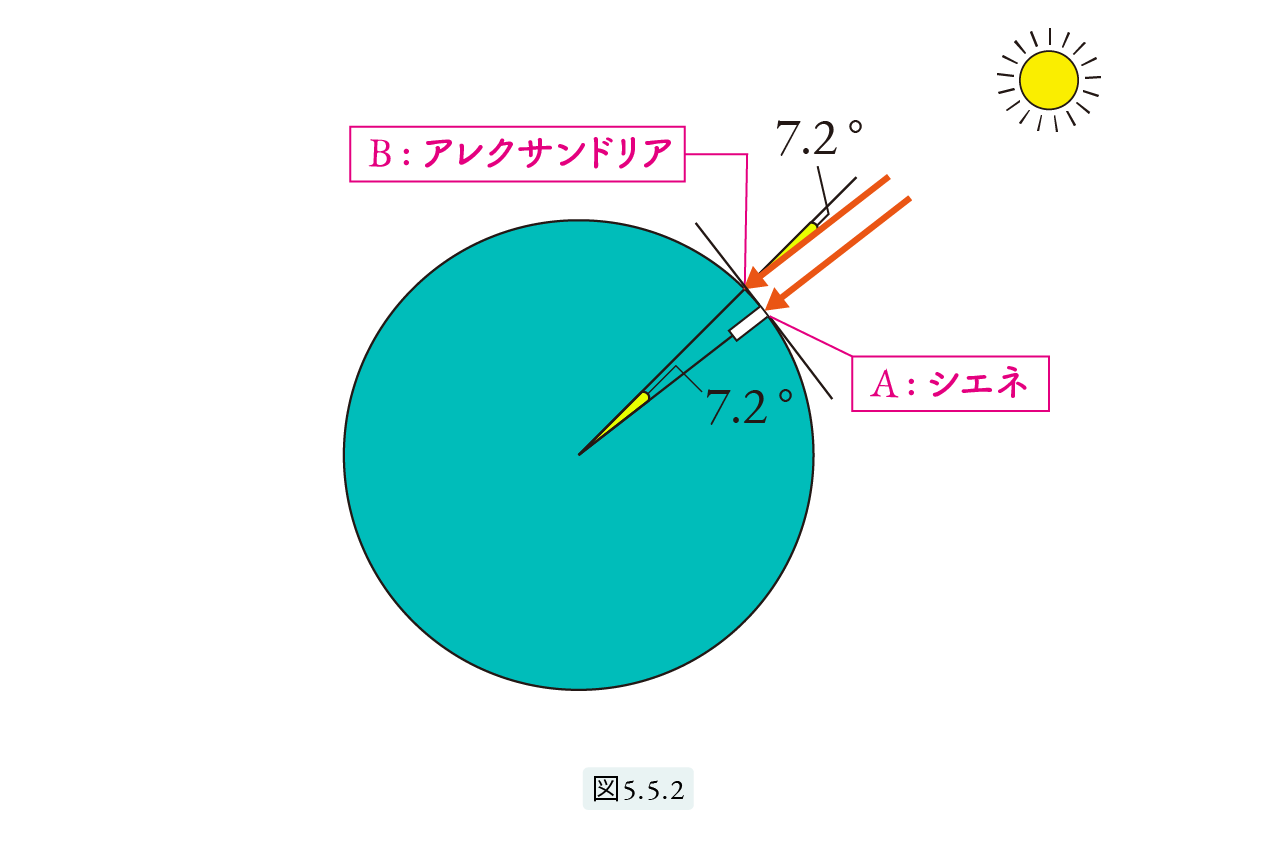
7.2 ÷ 360 = 1 50 ですから、7度12分は地球1周 360度の1 50 であることが分かったのです。そこでエラトステネスは、同じ歩幅で歩いて距離を測るように訓練された「ベバティステス」と呼ばれる測量士を使って、シェネとアレクサンドリア間の距離を測りました。その結果は「5000スタディオン」でした。シェネとアレクサンドリア間は地球の 1 50 ですから、地球の周長は 5000 × 50 = 25万スタディオンとなります。
1スタディオンが現在の単位でどのくらいになるか、いろいろな説があります。小さいものでローマ・マイルを根拠とした 148.8メートル、エジプト尺を根拠とした158メートル、最も大きく見積もったものでも166メートルです。どの値を取るにしても、実際の地球の周長の 4万キロメートルに非常に近い値となります。たとえば 1スタディオン=160メートルとすると
250,000×160 m = 40,000,000 m = 4万キロメートル
となります。
古代の地球測量の疑問点:球形説と太陽の位置、精度の問題
この地球の測量にはむかしからいろいろな疑問点が指摘されています。上のお話の理論的前提として、地球が球形であるという地球球形説と、太陽が無限遠点にあって、太陽が射す角度はシュネでもアレクサンドリアでも同じだという仮定のもとで行っています。地球が平らでも、太陽が近くにあれば同じ状況が起きます。図5.5.3 で、Aはシュネ、Bはアレクサンドリアです。ABが水平であっても、B点で影ができます。
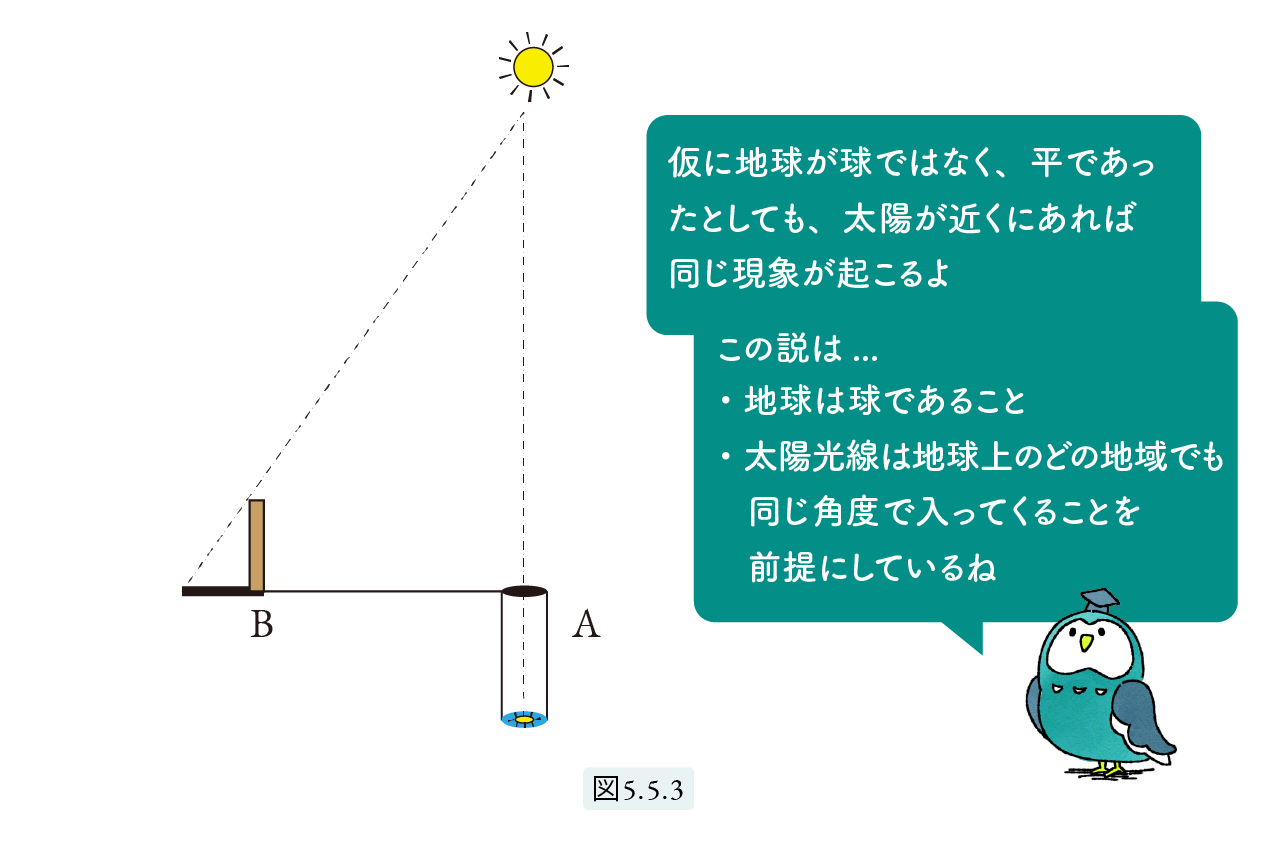
地球が丸いことと、太陽光線は地球上のどの地域でも同じ角度で入ってくるということは、現代の皆さんにとっては常識だと思いますが、古代においては果たしてどうだったでしょうか。海辺に立って地平線に向かう船を見ると、下から順に消えていき、最後にマストが消えます。このことから古代の人は地球が球だと考えた、とよくいわれます。しかしこれは、地球が球だと分かった後で思いついたのだと思います。古代ギリシア人は、ものが見えるのは光が眼に入ってくるからではなく、眼から“視線”が放出されるからだと考えていました。投げたボールが曲線を描くように遠くを見ると視線も曲がる、と考えても不思議はありません。そもそも「船が下から消えていく理由」など考えることなどなかったと思います。物が見えるのは光が眼球に入ってくるからだということ、光は直進することなどを発見し、光学の基礎を築いたのは、イラクで生まれエジプトで活躍した10世紀のアラビアの天文学者イブン・アル=ハイサムです。「地球球体説」とか「太陽が無限遠点にある」ということは、頭の中だけで思いつくものではなく、何百年にもわたり天体を観測した経験と観測データから導かれたものだと思います。さらに大きな問題は、精度についてです。太陽は点ではなく円です(視角0.5度)から、影の長さを正確に測ろうと棒の長さを長くすると、影がぼやけてしましますし、棒が短いと精確には測れません。当時のシュネがどこにあったかははっきりしませんが、シェネがあったとされる現在のアスワンは真南ではなく真南より数度東にずれているようです。また、正確な時計も方位磁石もなかった古代にシェネがどうして真南にあることが分かったのでしょうか。シェネまでのくねくねと曲がった道を、直線距離として精確に歩いて測れるものなのでしょうか。
緯度と経度が入った地図がいつ頃成立したか
歴史や数学史の専門家は、「精度は問題ではない。大切なのはどのようにして地球の周長を測ったか、という原理なのだ」と述べている人が多いようです。しかし問題はそれほど単純ではありません。「緯度と経度が入った地図がいつ頃成立したか」という問題に関連するからです。
ストラボンとクレオメデスの地理学
ここで、エラトステネスの「地球の周長の測定」の伝承の元になったものを探ってみましょう。エラトステネスより200年ほどあとの古代ローマ時代に、ストラボンという有名な地理学者がいます。ストラボンは『地理書』という著書を書き、その中でエラトステネスの書いた地図を何度も引用しています。その地図には緯度も経度も書かれていたようです。ストラボンの著作は広く読まれ、そのためかエラトステネスは緯度・経度を用いた地図の発明者とされることがあります。
しかしストラボンはエラトステネスの「地球の周長の測定」については触れていないようです。このお話の最も古いものは、古代ローマ時代に書かれたクレオメデスの『地球の測量』という地理書のようです。この人物に関しては名前のほかには何もわかっていませんが、この著作はよく引用されています。その後の引用では、地球の周長を「25万2千スタディオン」となっているようです。なぜ2千スタディオンが加えられたかというと、360で割り切れるようにしたかったためではないかと考えられています。360で割り切れれば、
緯度1度の距離 = 252,000スタディオン ÷ 360 = 700スタディオン
となり、地図の製作などに便利です。
最近の研究によると、著書の内容から判断してクレオメデスは4世紀頃の人のようです。そうだとすると奇妙なことが判明します。この『地球の測量』にはプトレマイオス※のことがなにも触れられていないのです。
プトレマイオス(90年頃~168年頃)は古代ローマ時代、エジプトのアレクサンドリアの近郊に住んでいた地理学者、天文学者、数学者です。英語名をトレミーといい、多くの著作を残しヨーロッパの科学の初期の発達に大きな影響を及ぼしました。現代の幾何学でもトレミーの定理はよく知られていますし、三角関数の基礎を築いた人としても有名です。ヨーロッパの大航海時代の前によく使われていた地図は、何とプトレマイオスの地図でした。プトレマイオスの名はアルキメデスと共に古代から鳴り響いていました。したがって、4世紀のクレオメデスがプトレマイオスのことを知らないはずはないのです。
プトレマイオスは地図の製作にエラトステネスが計算した「地球の周長=25スタディオン」を用いていません。彼が用いたのは、エラトステネスより100年後の天文学者ポセイドニオスが計算した「地球の周長=18スタディオン」です。ポセイドニオスは、シリアで生まれ、ロドス島で研究活動をしました。地球の周長の求め方はエラトステネスと同様です。彼はアレクサンドリアとロドス島との距離、2つの緯度の差を用いました。ただし、緯度の測定は、太陽の影ではなく星を観測したのだと思います。プトレマイオスはなぜエラトステネスの求めた値を使わなかったのでしょうか? 存在を知らなかったのか、そのような事実はなかったからでしょう。
正確な地図はいつ出来上がっていたか
「夏至の日にシェネでは太陽が井戸の底まで差し込むことを知ったエラトステネスは、これを利用すれば地球の周長が計算できることに気がついた」というお話はとてもよくできたお話で、教育効果も抜群でしょう。でもこれは本当にあったことなのでしょうか。
古代ギリシアの船乗りはフェニキア人から航海術を習いました。このことはいろいろな文献に出てきますが、ストラボンも著作の中で次のように書いています:「昔ギリシアの船乗りは、昼間陸地からあまり離れていない所しか航海できなかったが、フェニキア人から、こぐま座の位置で天の北極を知る方法を教わり、夜でも陸地から離れた海原を航海できるようになった」。エジプト王朝時代のファラオも、南に行くと太陽は真上に輝き、さらに南に行くと太陽が北の空に輝くことを知っていました。このように、古代の人は星や太陽の高度がその土地ごとに異なることを知っていました。エジプトではさらに古く古墳時代でも、ファラオは死ぬと、決して沈むことのない北の空の星(このような星を周極星といいます)になると信じており、祭殿の玄室にその星の光が差し込むようにその星の高度を正確に計測していました。また上で述べたように大ピラミッドの方位がきわめて正確に計測されています。エジプト人の計測技術を用いれば、太陽の影のような不正確な方法を用いなくても、星を使ってもっと正確に緯度を計測できたと思います。エラトステネスのお話のように、1年にたった1回夏至の日にしか起きないような現象を利用する必要などなかったと思います。
上で、エラトステネスはシェネとアレクサンドリアの間の距離を測量士を歩かせて測ったと述べました。エジプト文明は整った官僚制度のもとで3千年も長く続いています。また、ヘロドトスも言っているように測量技術は発達して、毎年洪水が起きるたびに何度も測量がなされてきていたと思います。エラトステネスの時代には、わざわざ測り直さなくてもすでに正確な地図ができ上っていたと思います。
エラトステネスの地図の謎とその真偽
エラトステネスのお話が本当だとすると、もう一つ不可解な点があります。エラトステネスが地図を書いたという伝承です。その地図は緯度・経度を用いた世界地図で、エジプトだけでなく地中海全体を含んだものです。ストラボンはこの地図のことを何度も引用しています。エラトステネスの地球の測定のお話を最初に書いたとされるクレオメデスはエラトステネスより約500年も後の人です。現在の日本で言えば関ヶ原の戦いぐらい前のことです。これに対しストラボンは約100年後ですから、エラトステネスが世界地図を製作したということは十分ありうるように思います。だとすると、エラトステネスがはじめて「緯度1度の長さを計算した」ということはあり得ません。古代のことですから土地の測量には非常に時間がかかります。エジプトの地図ならまだしも地中海全域を含む地図ですから、地図の完成には何十年も、ことによると百年以上かかったことと思います。エラトステネスの地図は早くに失われてしまったという説もありますが、ネットで調べると複数出てきます。
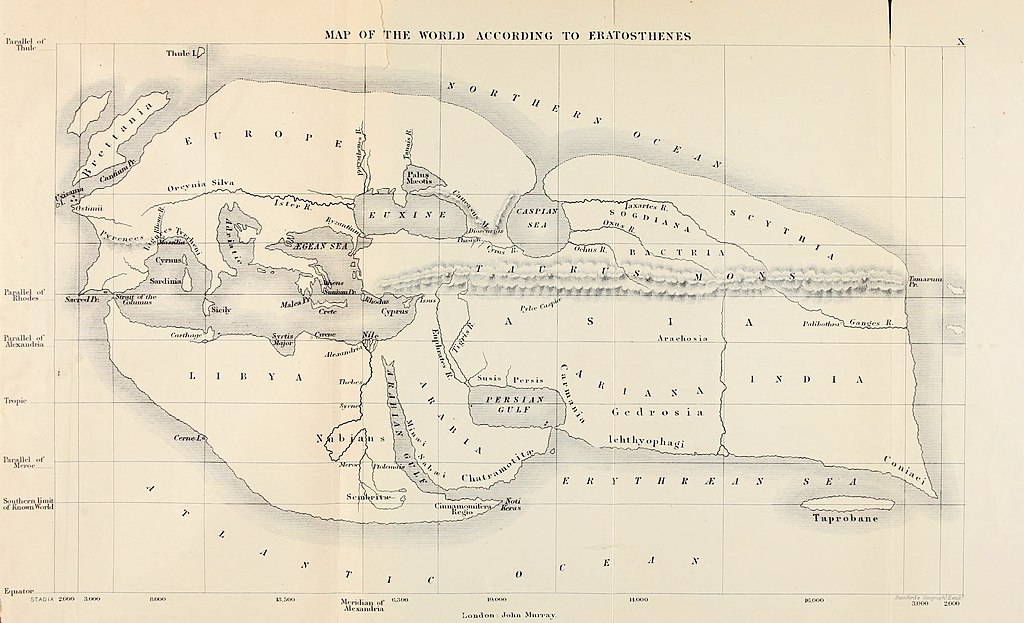
これらの地図が後世に捏造されたものなのか、あるいは本物が何度もコピーされて現在まで続いているのか、真偽ははっきりしませんが、エラトステネスの地図が広く流布していたことは確かだと思われます。
エジプトの地図と緯度測定・エラトステネスの地図
これからは前回『5-6.ピラミッドの『地球尺度の謎』を解明する』地球尺度の謎で述べた仮説4の続きです。エジプト人は大ピラミッドの緯度が正確に30度であることに気づきました。あるいはこれがギザにピラミッドを建てた理由かもしれません。もちろんピラミッドの時代には円1周360度という角度はありませんが、末期王朝時代にはバビロニアからこの角度が入ってきます。バビロニアではこの角度を使って星々の座標を表していました。エジプト人はこの制度を土地に応用したと考えることは自然だと思います。
仮説4の主張は、エジプト人は天の北極の高さ(つまり緯度)を土地の番地としていた、ということです。これはエジプトが南北に伸びる1次元の世界だったから可能だったと思います。エジプト人が星の高さを表すのにバビロニアの角度を用いるようになったのは自然な成り行きです。バビロニアから 360度の角度が入ってくる前から、東西南北の線が入った正確な地図はあったと思います。エジプトには縄師と呼ばれる測量士がいましたし、優秀な官僚書記が取り仕切っているのですから地図がないはずはありません。星の高さの単位をバビロニアの角度に変えることによって、エジプト人は緯度が明示された詳細なエジプトの地図を作っていたに違いありません。方位の概念がしっかりしていますから、シェネが真南にある必要はありません。またわざわざ歩いて距離を測る必要もありません。
当時(末期王朝時代)多くのギリシア人がエジプトに傭兵として雇われていました。そのためエジプトとギリシアの交流も盛んでした。「ギリシア人は星で地を測る」という伝承が示すように、ギリシア人はエジプト人から緯度の計測の仕方を学んだものと思います。ギリシア人は地中海をわが海として交易を行っていました。こうした遠洋航海のためには地図が必須ですから、多くの地図が作られたと思います。ヘレニズム時代になって、文化の中心がアレクサンドリアに移ると、アレクサンドリアの大図書館には多くの地図が集められていたと思われます。
エラトステネスは大図書館の館長ですから図書館にあるパピルスの資料を自由に読むことができました。エラトステネスが編集したものが「エラトステネスの地図」と呼ばれるものだと思います。何百年もたち、「エラトステネスの地図」だけが継承されると、「エラトステネスが緯度の発明者」とされても不思議ではありません。そのうえ、「シェネでは夏至の日太陽が井戸の底に写る」という興味深い現象知って、作家の創作意欲が掻き立てられたのだと思われます。