ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
5-1.ピラミッドの『円周率の謎』を解明する(1)
ページ目次
ピラミッドの『円周率の謎』のおさらい
いよいよピラミッドの謎を解きましょう。謎は解かれてみると、驚くものでも何でもないごく常識的な解のような気がします。ですから、これらの解は部分的にはすでに誰かがそれとなく述べているかもしれませんが、それらをつなぎ合わせて一つの解としてまとめて述べてはいないのではないかと思います。
本連載では、数学の話だけでなく歴史や神話の話もしてきました。むしろ数学の話はあまり出てきませんでした。しかしこの章を読んでいただければ、一見無関係に思える話が思わぬところでつながっていることが分かると思います。ピラミッドの謎の一番大きな解答は、「古代エジプト人は意外と数学を知っていた」ということになります。
本連載のはじめの節に述べたピラミッドの円周率の謎についてもう一度振り返ってみましょう。
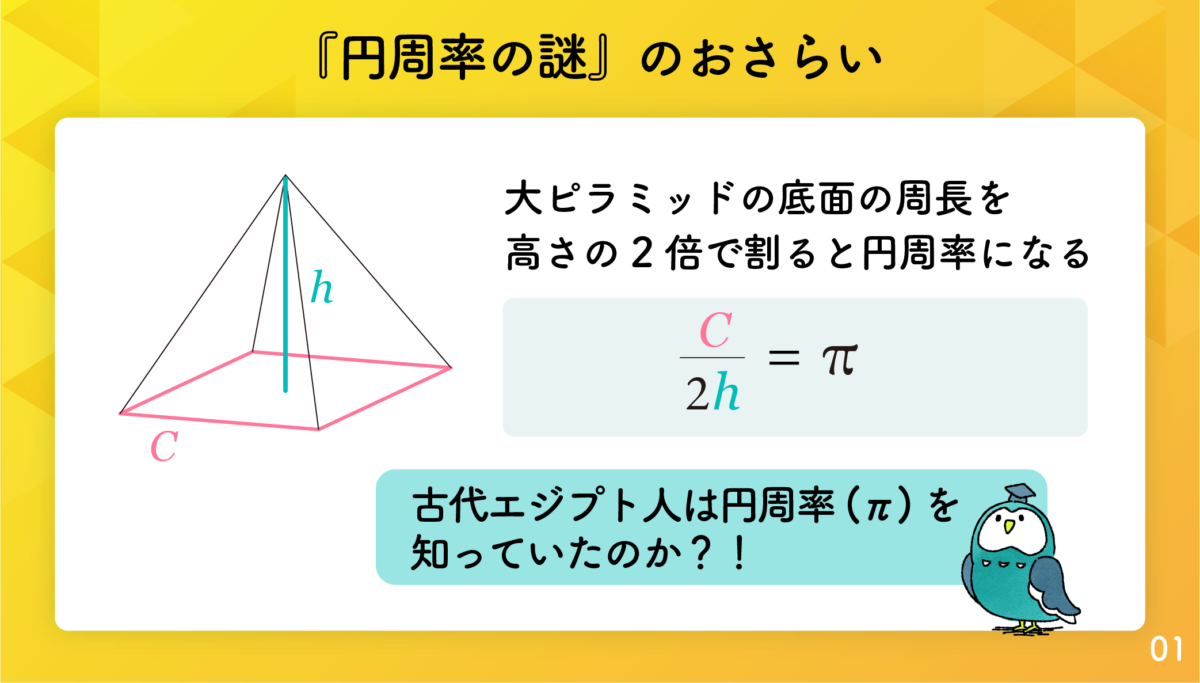
円周率の謎大ピラミッドの底面の周長を高さの2倍で割ると円周率になる
図1.1.1は周長が C で高さが h のピラミッドです。円周率の謎は「C 2h = π」が成立する。
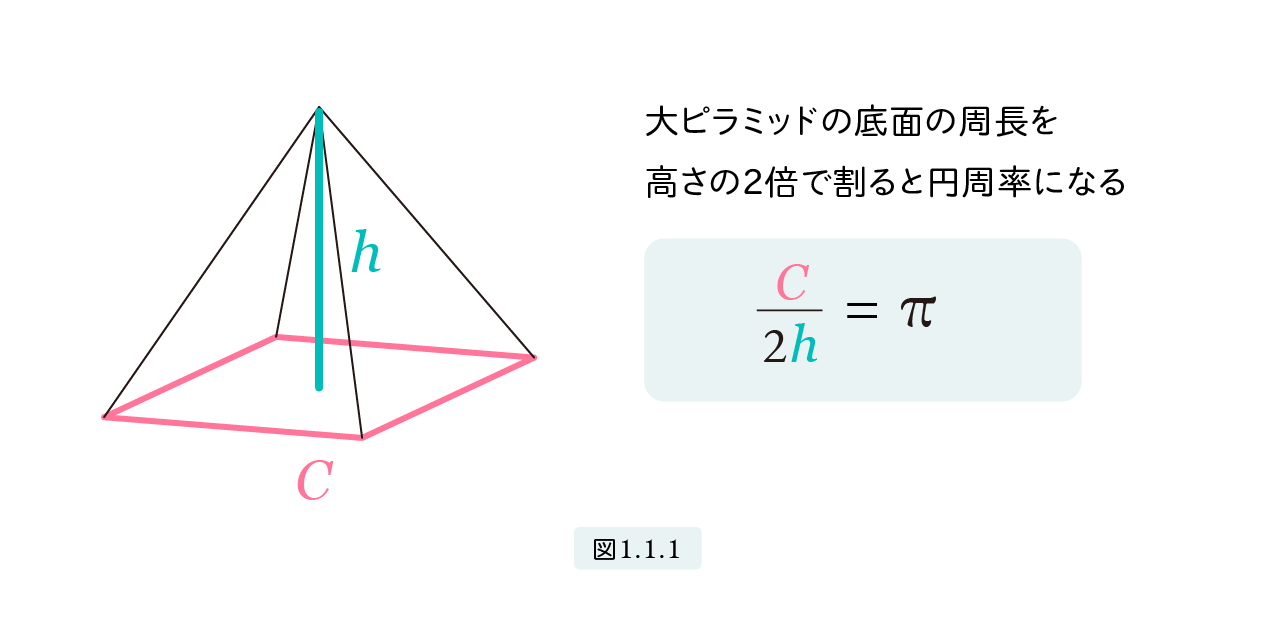
古代エジプト人は円周率 π を本当に知っていたのでしょうか。これが、ピラミッドにまつわる円周率の謎です。
関連記事以下の記事で詳しく解説しています++。
ピラミッドとセケドの関係
ピラミッドの謎で一番留意すべきなのは「偶然説」で、「たまたまそうなったにすぎない」という説です。Chapter1では、クフ王のピラミッドに注目しましたが、クフ王のピラミッドだけでは「偶然説」を退けることはできません。また、測定値にも問題があります。すでに建造されてから数千年もたっており、てっぺんの笠石もなくなり、表面も風化しています。本節ではクフ王のピラミッド以外のピラミッドにも着目し議論を進めていきます。
『3-2.比と傾き』で、エジプト人はピラミッドの傾斜をセケドで測っていることが分かりました。セケドは、現代の傾きと同じで、少々表面が破損していても、笠石がなくなっていても大体の数値が予測できます。セケドの復習をしておきましょう。
●セケドのおさらい
ここでは『3-2.比と傾き』でも述べた、傾きとセケドの関係性の式を使います。
セケドと傾き 傾き = 7 勾配, 勾配 = 7 傾き
具体的に底辺と高さを入れて考えてみましょう。図5.1.1 は底辺が a、高さが h のピラミッドです。
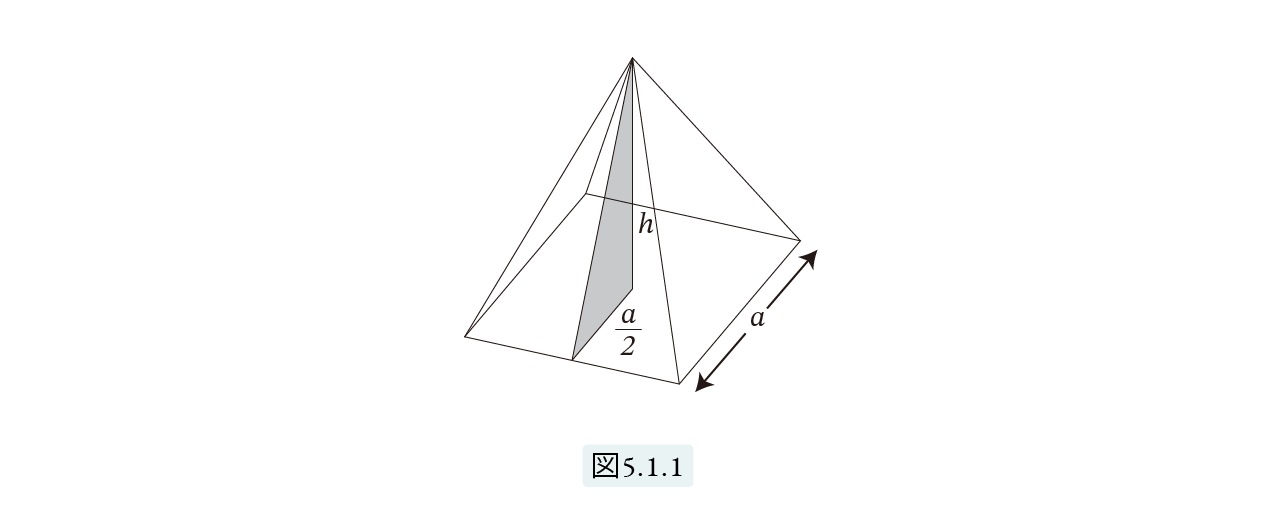
傾きやセケドは、図のようにピラミッドを切断してできる直角三角形で計算します。この直角三角形の底辺の長さは a 2 ですから、
傾き = h a2 = 2h a
セケドは傾きの逆数を7倍したものですから
セケドの計算式 セケド = 7×a 2h (1)
となります。
関連記事以下の記事で詳しく解説しています++。
代表的な4つのピラミッドとその共通点
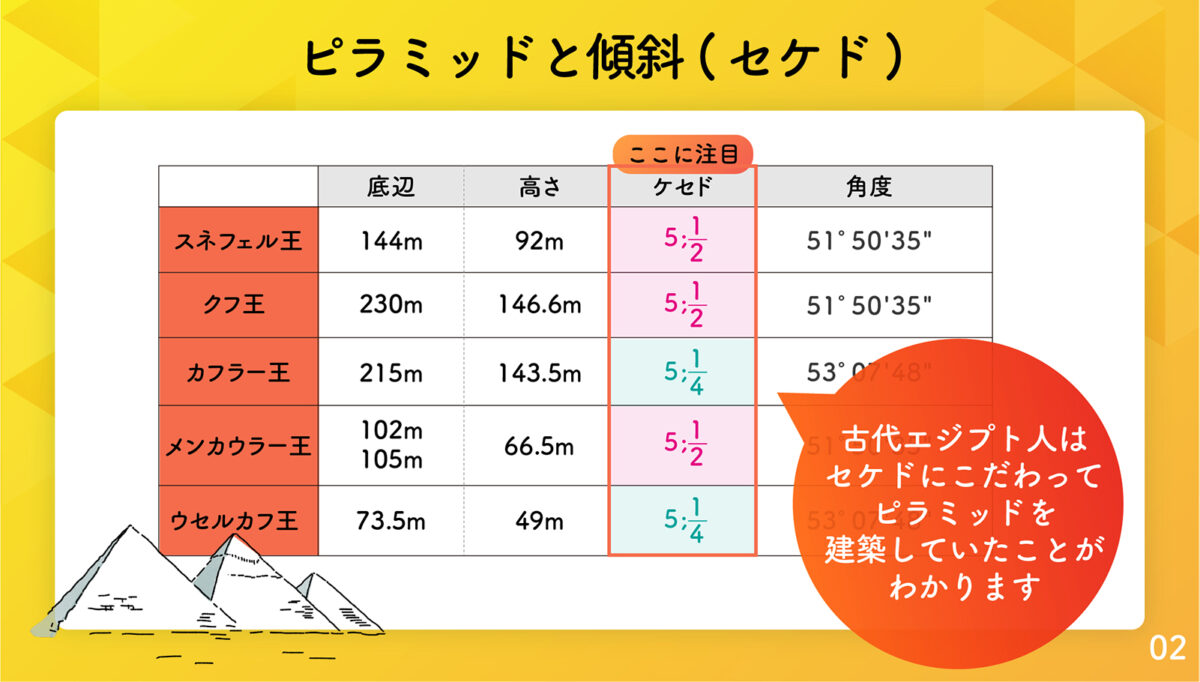
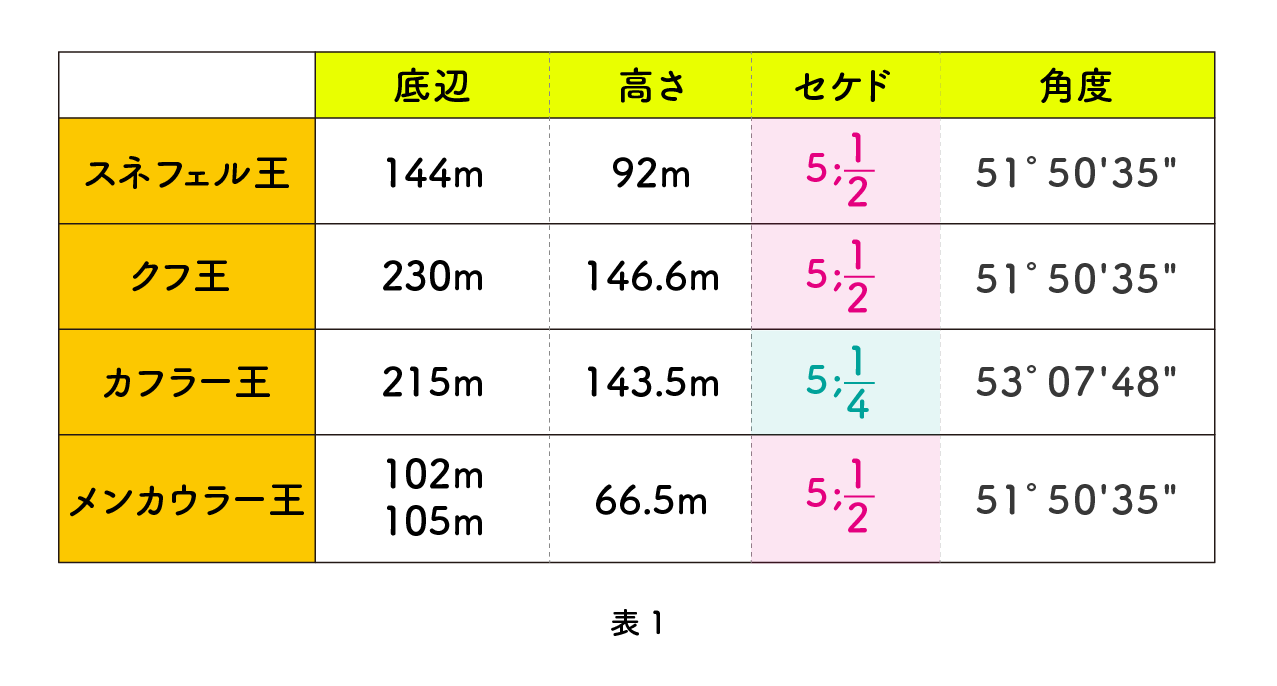
まずはスネフェル※、クフ※、カフラー※、メンカウラー※の4つのピラミッドについて検証していきます。資料によって多少の差がありますが、それぞれの底辺と高さから、セケドを計算してみましょう。
スネフェル王のピラミッドのセケド
底面が正方形の「真正ピラミッド」が作られるようになったのは第4王朝のスネフェル王からのようです。それ以前は石ではなく、干乾し煉瓦で造られた階段式ピラミッドでした。スネフェル王は3つ(あるいは4つ)もピラミッドを造ったといわれていますが、真正ピラミッドは最後に作ったピラミッドで、底辺が144メートル、高さが92メートルですから、上のセケドの計算式 (1)式を使ってセケドを計算すると、
セケド = 7 × 144 2×92 = 5.48 ≒ 5;1 2
となります。スネフェル王のピラミッドについてはまた次回でもふれます。
クフ王の大ピラミッド
ギザの有名な3つのピラミッドの一つです。なかでもこのクフ王の大ピラミッドが、規模や石積の技術などにおいて最高水準を示しています。クフ王の大ピラミッドの横には2つのピラミッドが並んでいます。クフ王の隣はクフの後継者カフラーのピラミッドで、その隣がカフラーの後継者のメンカウラーのピラミッドです。それぞれが葬祭殿などの建物を含むピラミッド複合体を成しており、ピラミッド建築の最盛期の姿を現在に留めています。王の権力や経済力のせいかもしれませんが、建築技術や数学などの学術なども、つねに進歩するのではなく、停滞したり、ときには衰退することがあるのかもしれません。
セケド = 7 × 230 2×146.6 = 5.49 ≒ 5;1 2
カフラーの大ピラミッド
カフラーやメンカウラーのピラミッドは、資料によって多少の差がありますが、カフラーのピラミッドは、だいたい底辺215がメートル、高さ143.5メートルのようです。
セケド = 7 × 215 2×143.5 = 5.244 ≒ 5;1 4
となります。セケドは 5;1 2 ではなく 5;1 4です。これについてもあとで議論します。
メンカウラーの大ピラミッド
メンカウラーのピラミッドは前の2王に比べるとはるかに小さく、高さが半分になっていますから体積は 8 分の 1 となります。また、データも資料によって差があるので、底面は 102×105メートルの長方形、高さは66.5 メートル という値を採用します。
建築技術が落ちたせいか、底面は正方形ではなく長方形です。したがって、傾きが2通りとなります。比較のために角度も計算しておきます。
66.5×2 102
= 1.304, 勾配 52.516°= 52°31′
66.5 × 2 105
= 1.2666, 勾配 51.71°= 51°43′ セケド = 5.5260 ≒ 5;1 2
105メートルで計算すると、セケドは 5;1 2 と見なしてよいと思われます。また、角度は52°とみなしてよいでしょう。底辺が102m、105mの2つの場合を計算しましたが、角度の差は1度以下です。下図で示されるように、1度の差はほんのわずかです。
以下では 上で採用した52°がよく出てくるので覚えておいてください。

セケドと角度
上では現代の計測値を使ってセケドを求めました。しかし、メートルは現代の単位ですし、計測には誤差が含まれます。セケドから傾きと角度を計算しておきましょう。ここで、セケドと傾きの復習をしましょう。上で見たピラミッドのセケドは 5;1 2 と 5;1 4 の2種類が出てきました。セケドと傾きの関係は、「逆数をとって 7 倍」です。したがって、
セケド 5;1 2 = 傾き 14 11 、 セケド 5;1 4 = 傾き 4 3
となります。次に角度と傾きの復習です。図5.1.2を見てください。
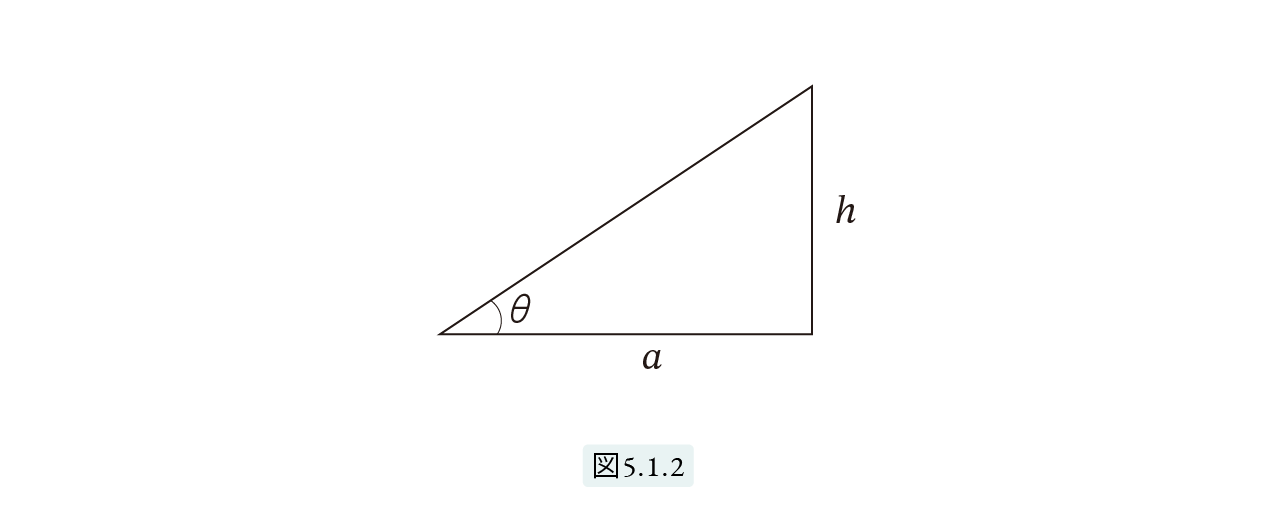
角度θがわかれば傾き h a がわかります。関数電卓を使えば、傾きは tanθ で計算できます。逆に、傾き h a がわかっているとき、角度θは
θ = tan-1(h a )
で計算できます。関数電卓を使って、傾き 14 11 と 4 3 の角度を求めてみましょう。
tan-114 11 = 51.84277341 = 51°50’34”
tan-1 4 3 =51.84277341 = 53°07’48”
まとめると、次のようになります。
セケド 5;1 2
= 傾き 14 11
≒ 角度 52°
セケド 5;1 4
= 傾き 4 3
≒ 角度 53°
セケド 5;1 2 と セケド 5;1 4 の角度の差はたった1度です。
その他のピラミッドは?
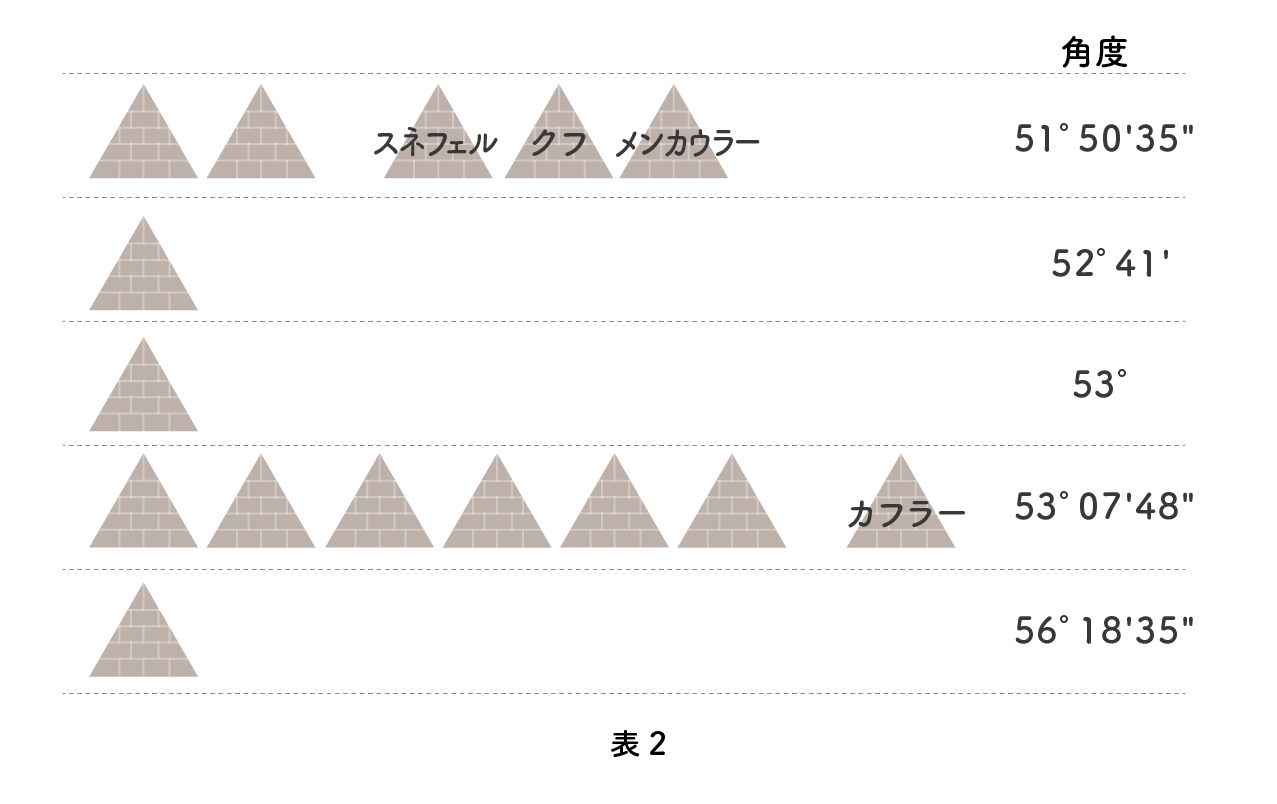
それでは他のピラミッドはどうでしょうか。『宇宙考古学―人工衛星で探る遺跡と古環境 (丸善ライブラリー)』にその他のピラミッドのデータがありました。対象となるのは第4王朝から第6王朝までの真正ピラミッド(底面が正方形の四角錐)のものだけに限ることにします。第5王朝になると規模や技術がだいぶ落ちて、第6王朝になるとさらに落ち、現在では崩れて原形をとどめていないものが多くなります。拾い出したのは全部で11個で、これにギザの3つのピラミッドとスネフェル王のピラミッドを加えると、ピラミッドの数は 15 となります。
秒の単位まであるのは実測値ではなく傾きから計算したからだと思われます。『宇宙考古学』の第5王朝のウセルカフ王のデータは、傾きの値が計算違いのようなので計算しなおしました(サフラー王の傾きも訂正しました)。ウセルカフ王のピラミッドの底面の1辺は 73.5メートル、高さは49メートルですから、傾きは
傾き = 49/((73.5 / 2) )= 4 3
となり、とてもきれいな数値になりました。これは間違いなくセケド 5;1 4です。
確認のために、4行目の角度 53°07’48” から直接傾きを計算してみましょう。この角度は60進数ですから、まずこれを 10進数に変換します。
53°07’48” = 53 + 7 60 + 48 602 = 53.13
関数 tan を使って、これを傾きに直します。
tan 53.13 = 1.33333 ≒ 4 3
上のデータをまとめましょう。表2’を見てください。3行目の 53°はほとんど 53°07’48” とみてよいでしょう。51°50’35” はクフ王のピラミッドと同じで、セケド 5;1 2 。53°07’48” はカフラー王のピラミッドと同じで、セケド 5;1 4 です。まとめると、5個がクフ王と同じセケド 5;1 2で、8個がカフラー王と同じセケド 5;1 4、残りの 2 個は例外です。
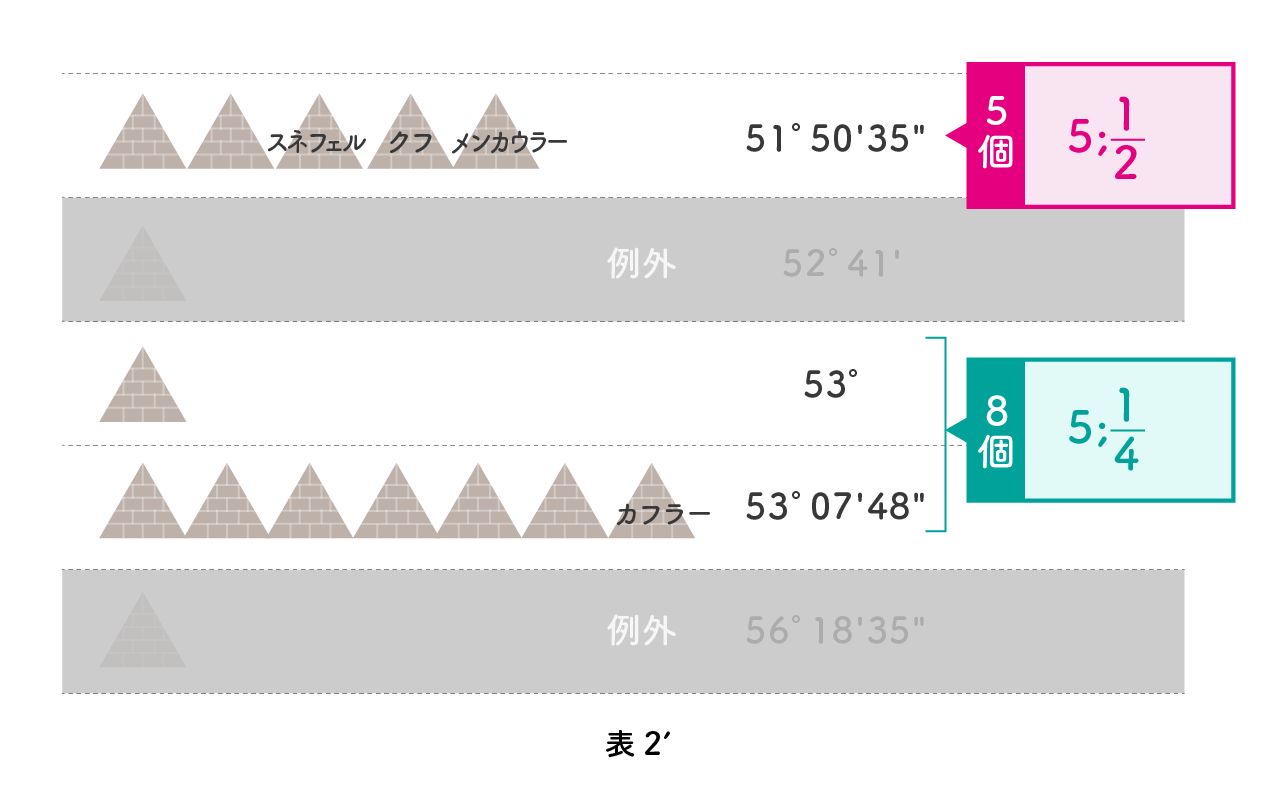
この表から明らかなように、ピラミッドはセケドを基準に作られています。セケド 5;1 2 とセケド 5;1 4 です。途中から、セケド 5;1 2 からセケド 5;1 4 に変更されたようです。この理由については後で考えますが、たった1度の差でしかなく、人間の目には差が分からないことに注意してください。エジプト人は見た目の美しさではなく、数値にこだわっていたことが分かります。
当時の単位で確認してみる。
これらのデータから、ピラミッドはセケドを基準に作られているのは間違いないと思いますが、念のため、当時の単位で確認してみましょう。ピラミッドの計測は現在の長さの単位メートルを使ってなされています。ニュートンは、大ピラミッドは腕尺を使って正確に造られていると指摘しています。これを確かめてみましょう。クフ王のピラミッドの計測値は、1辺が 230.37メートル、高さが 146.6メートル、1腕尺=0.524メートル ですから、
1辺 = 230.37÷0.524= 439.6374046 ≈ 440 (腕尺)
高さ= 146.6 ÷ 0.524=279.7709924 ≈280 (腕尺)
ほとんどぴったり、440腕尺、280腕尺となります。
上ではメートルで測った計測値を使ってセケドを計算しました。こんどは今得た腕尺を使って直接セケドを計算してみましょう。
セケド = 7 × 底辺 高さ =7 × 220 280= 11 2 =5;1 2
上で得たセケドは概算値でしたが、今度はぴったりと 5;1 2 となりました。ピラミッドがセケドで設計されていたことはまちがいなさそうです。
ピラミッドの『円周率の謎』を数学的に解明する
ほとんどのピラミッドが、見た目の美しさだけにこだわり形をきめたのではなく、セケド 5;1 2と5;1 4という数値を基準につくられていることがわかりました。次に、ピラミッドの円周率の謎とセケド 5;1 2 の関係を述べましょう。次の命題は数学的に証明可能なので事実としました。
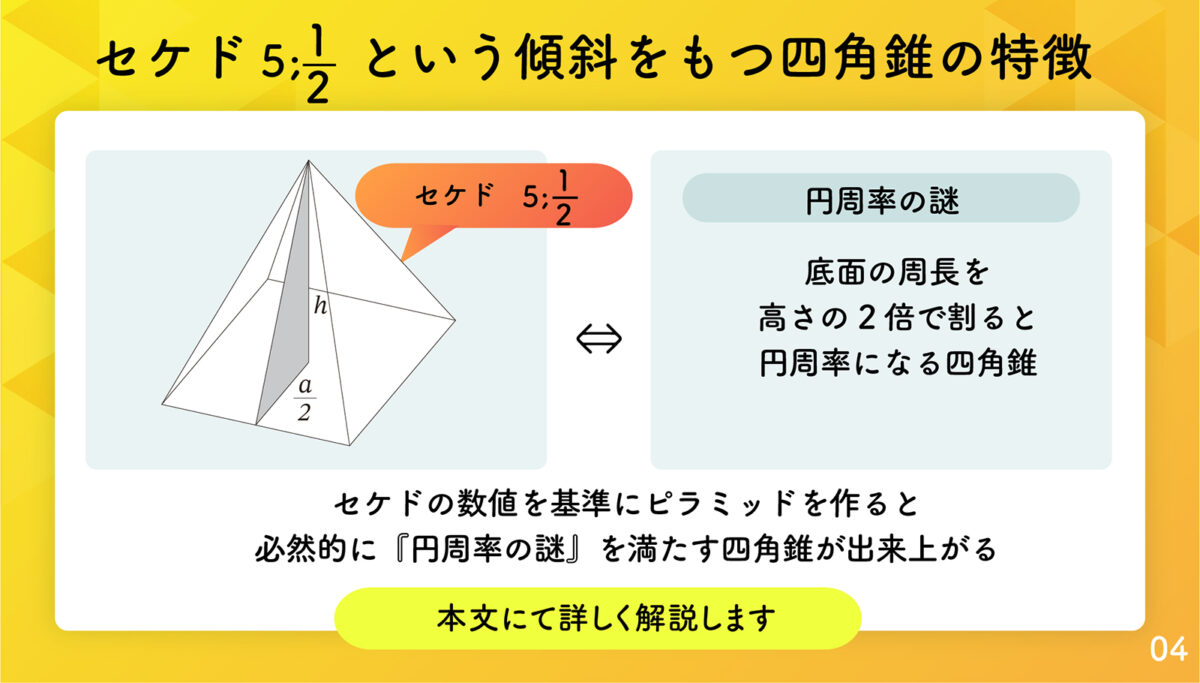
事実1 ピラミッドのセケドは 5;1 2 ⇔ ピラミッドは円周率の謎を満たす
高さ h、底面の1辺が a のピラミッドを考えます。図5.1.1。

このピラミッドのセケドが 5;1 2 だったと仮定しましょう。すると、傾きは 14 11 ですから
h/(a/2) = 14 11 よって h = 7 11a
このピラミッドの底面の周長は 4a です。
半径 h の円周 = 2πh = 14π 11 a = 3.99839a ≈4a = 底面の周長
となり、ほとんど「底面の周長=半径 h の円周」が成立します。
念のため逆も証明しておきましょう。図5.1.1のピラミッドで、4a = 2πh が成立したとしましょう。傾きは 2h a = 4 π ですから、
セケド = 7 × a 2h = 7×π 4 ≈ 5.49779 ≈ 5.5 = 5;1 2
となり、ほぼ成立します。
以上より、セケド 5;1 2 のピラミッドはすべて円周率の謎を満たすことが分かりました。
まとめ
以上より、古代エジプト人はピラミッドの傾き、セケドにこだわってピラミッドを建設していたことが明らかになってきました。円周率の謎では、円周率にこだわってピラミッドが建設されたのでは?という謎が含まれていましたが、上のセケドを基準にピラミッドを作ると必然的に円周率の謎をみたす四角錐になるのです。
ではなぜセケド 5;1 2 なのでしょうか。そしてセケド 5;1 2 はなぜセケド 5;1 4 に変更したのでしょうか。これらの数値はエジプト分数になじんだエジプト人にとっても決して切りのいい数ではありません。なぜ切りのいいセケド 5 を選ばなかったのでしょうか。セケド 5;1 2 、セケド 5;1 4、セケド 5 は角度に直すと、それぞれおおよそ 52度、53度、54度で見た目にはほとんど変わりません。では、高さと底辺を適当に決めたら“たまたま偶然に”セケドが 5;1 2 と 5;1 4 になったのでしょうか。次回の記事ではさらにこれらを深掘りしていきます!