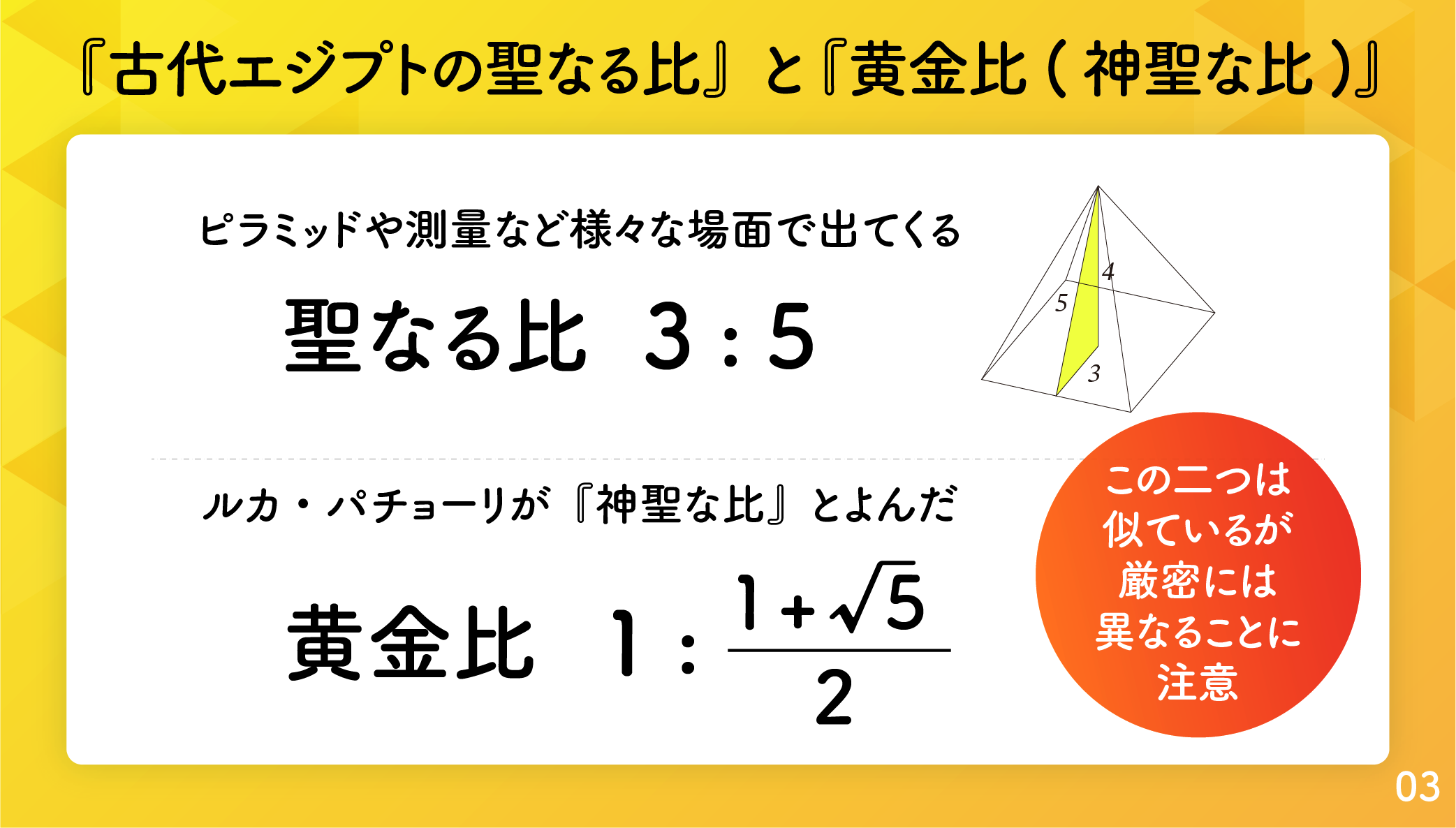
ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
5-4.ウィトルウィウス的人体図と黄金比
ページ目次
レオナルド・ダ・ヴィンチとプラトンの立体
ルネサンス期的教養人と数学
ルネサンス期はギリシアの幾何学が絶賛されおおいに持ち上げられた時代です。すべての分野に通じた博学の人を「ルネサンス期的教養人」と呼ぶように、当時の知識人は実に幅広い知識と教養を身に着けていました。何人もの芸術家は一流の数学者でもありました。多くの画家は、絵画をきわめるには数学が必要だと唱えています。ダ・ヴィンチ※も著書『絵画論』の冒頭で「数学に強くないものは、私の著作を読んではならない」と宣言しています。ただ数学の発展という観点からみると、当時の人が何か独創的な結果を出したということはありません。西ヨーロッパの数学や科学が急速に発展しだすのはもう少し後のことになります。数学の理解に関しては、ユークリッド※の『原論』の最初の数巻と黄金比を勉強していただけだったようです。しかし彼らの啓蒙活動が、その後の数学の発展に大きな影響を与えたことに間違いがありません。
黄金比に関して、その後絶大な影響を与えたのは、ルカ・パチョーリ※です。パチョーリは最初チェコという画家の工房で働いていました。チェコもまた後世に残る画家で、数学者でもあり数学の著作を残しています。パチョーリはこの工房を出て神学の勉強をし、修道士となります。彼は多数の数学の本を書いていますが、黄金比に関しては『神聖な比例』という本を書いています。この本のなかでは「プラトンの立体」とよばれる図形をレオナルド・ダ・ヴィンチが書いています。このイラストの正確さは有名です。
関連記事以下の記事で詳しく解説しています++。
パチョーリと黄金比:黄金比の再帰構造と神秘性
パチョーリは「黄金比」のことを「神聖な比」と呼んで、この本のなかでえんえんと美辞麗句を並び立てています。パチョーリは修道士でしたから、数学も神学の一部だと思っていたのでしょう。たとえば、黄金比には「小さい数、大きい数、その和」という3つの数が出てきますが、これをキリスト教の“三位一体”に例えています。また黄金比 が整数比では表せないことを「神は人間の尺度では測れないこと」を意味していると述べています。さらに、黄金比の再帰構造(つまり、「大きい数と2つの和」が「小さい数と大きい数」とみなされこれが永遠に続くこと)を、神の遍在性と普遍性を表すものだ、としています。パチョーリの用いた「神聖なる比」という名称と、この比の持つ摩訶不思議な神秘性が一般の人に受けたのでしょう。これ以降「神聖なる比」は広く世の中に広まります。しかし19世紀にもなると、科学万能の時代になり、“神”は一般受けしなくなったのかもしれません。「神聖なる比」という名称は「黄金比」にとってかわられます。(パチョーリの用語「神聖なる比」は、黄金比のことで、前回の終わりで述べた「聖なる比 5 : 3」とは異なることに注意してください。)
古代ローマの建築家ウィトルウィルスの著作とルネサンス期の数学の理解
ルネサンス期の数学の理解は、古典期のギリシアの数学のほんの初歩的段階にすぎませんでした。パチョーリやダ・ヴィンチが学んだのは『原論』などではなく、『4-6』で述べた古代ローマの建築家ウィトルウィルスの著作だったようです。パチョーリは『神聖な比例』において黄金比を讃えてはいますが、この比を実践において使うことには言及していません。むしろ実践においては上で述べたウィトルウィウスの著作にもとづいたさまざまな技法について述べています。ここには整数比しか出てきません。
レオナルド・ダ・ヴィンチは、パチョーリの『神聖な比例』のイラストを描いたことからも分かるように、パチョーリと親交を持ちます。ダ・ヴィンチはパチョーリから数学を学んだといわれていますが、その前から数学を勉強していたかもしれません。ダ・ヴィンチは正式な教育を受けたこともなくラテン語も理解できなかったと伝えられていますが、当時の人たちの多くは独学でした。上で当時は数学の独創的な進展はなかったと述べましたが、これは数学だけに限ったことで、ルネサンス期の人々はみな独創的で、すばらしい作品を残しています。ダ・ヴィンチはそのなかでも第一人者です。
--Advertising--
古代美術と黄金比
「ダ・ヴィンチの絵のなかには黄金比が隠されている」という説が多くの本で述べられています。これは本当でしょうか。絵を描いたり彫像を作ったりするときには比が重要です。8頭身とは「頭部と身体の比が 1 : 8」の体つきのことです。このため画家はキャンバスに格子状の補助線を引いてからデッサンをします。これをカノンといいます。この「カノン」はいつ頃から始まったのでしょうか。
古代ギリシアの美術と比(カノン)
古代ギリシア時代に戻りましょう。『4-1』で述べたように、ギリシア文明が華開く古典期の前は「東方化革命の時代」と言って、オリエントの文化を吸収している時代です。ちなみに、ピタゴラスが生きたのもこの時代です。この時期ギリシア世界の各地で神殿や彫像が作られます。男性の立像はクロース像といい、女性の立像はコレー像といいます。共に直立して動きがないのですが、これらはエジプトの立像からの強い影響が観察されています。特に顔、身長、肩幅などのカノンが一致しているといいます。
古代エジプトと美術と比(カノン)
エジプトの壁画には多くの人物像が描かれていますが、これらの像を描くのに像を細かい升目に区切って描きました。ファラオなどの重要な人物は大きく描き、重要でない人物は小さく描きます。人物の大きさは、実際のサイズではなく重要度を表しています。壁画は絵画というよりは説明文で、絵は文字と同じ情報を表すためのものでした。貢物などは上から内容がよく分かるよう描き、その下の容器は横から描きました。顔と腰から下は横向き、体は正面から描かれていました。エジプト人は伝統と形式を重んじており、サイズが変わってもつねに同じ比率で描かれていたのです。この形式をギリシアは受け継ぎました。
エジプトの彫像はただ立っているだけで、表情もありません。それに比べギリシアの彫像は躍動感にあふれ芸術的には格段に優れています。しかし、カノンについてはやはりエジプトが元祖だとみた方がよいでしょう。
レオナルド・ダ・ヴィンチと黄金比
ウィトルウィウス的人体図と黄金比
さて、黄金比で書かれていると言われている絵画は、正確に黄金比 1 : 1.6180 なのでしょうか、それとも前節で述べた『聖なる比 3 : 5 』なのでしょうか。実際に調べてみると、どれもどこからどこまでを測るのか、基準がはっきりせず判定できません。ただ一つの例外は、ダ・ヴィンチのウィトルウィウス的人体図です。題が「ウィトルウィルス的」となっている以上、ウィトルウィルスの著作を参考にしていることはまちがいありません。そしてこの絵には円と正方形が書かれているため、測る対象が明確で疑問の余地がありません。つまり、「円の半径 : 正方形の1辺」が黄金比となっているか、です。ダ・ヴィンチはパチョーリの友人ですから、従来からこの比は黄金比であると誰もが思ってきました。映画のダ・ヴィンチ・コードに出てきましたから、皆さんの中にもご存知の方がいらっしゃると思います。
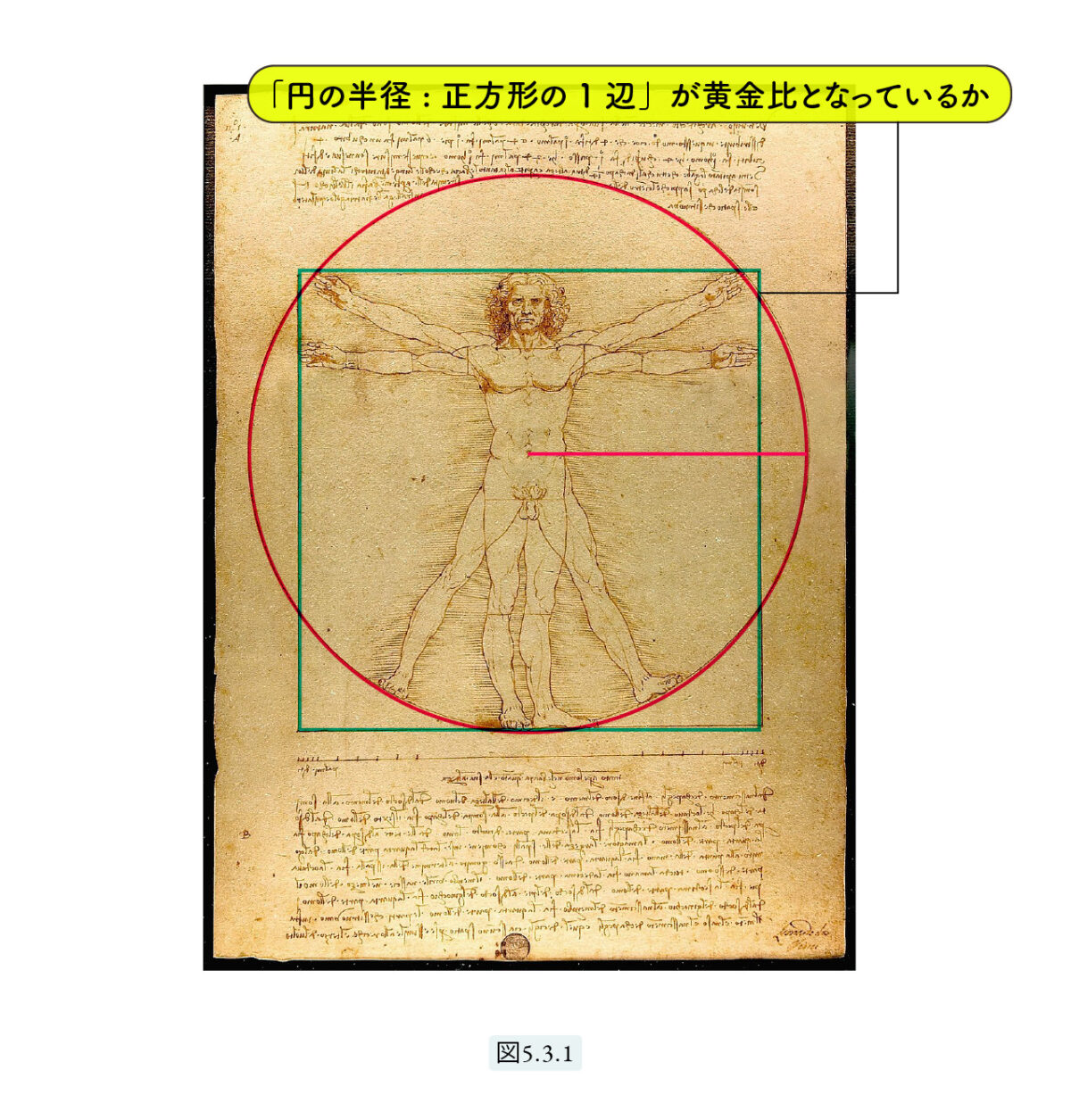
ウィトルウィウスの機械論
この図を解析する前にウィトルウィウスの『機械論』に出てくる言葉を紹介しておきます。「建築は人体と同じように調和したものでなければならない。」(近代建築の巨匠コルビュジェもこれと同じことを言っています。)「頭のてっぺんから足の裏までの長さと、両手を広げたときの長さは、正方形の高さと幅と同様に等しい。人体の中心は当然臍(へそ)である。人間があおむけに寝て手足を伸ばすと、臍を中心にコンパスで描いた円に手足の先がふれる。」 また、ウィトルウィルスは、理想的な人体の比率を定義しました。もちろん彼の用いた比は整数比でした。ダ・ヴィンチもこれに従ったに違いありません。
ウィトルウィウス的人体図の比を実際測ってみる
「円の半径 : 正方形の1辺」は実際に測ってみればすぐわかります。ある文献では1.656 とありましたが、実際測ってみても 1.64… から 1.66… くらいになります。この値は正確な黄金率 φ = 1.6180 とはだいぶ異なり、聖なる比 5 3 = 1.666… とほとんど一致します。
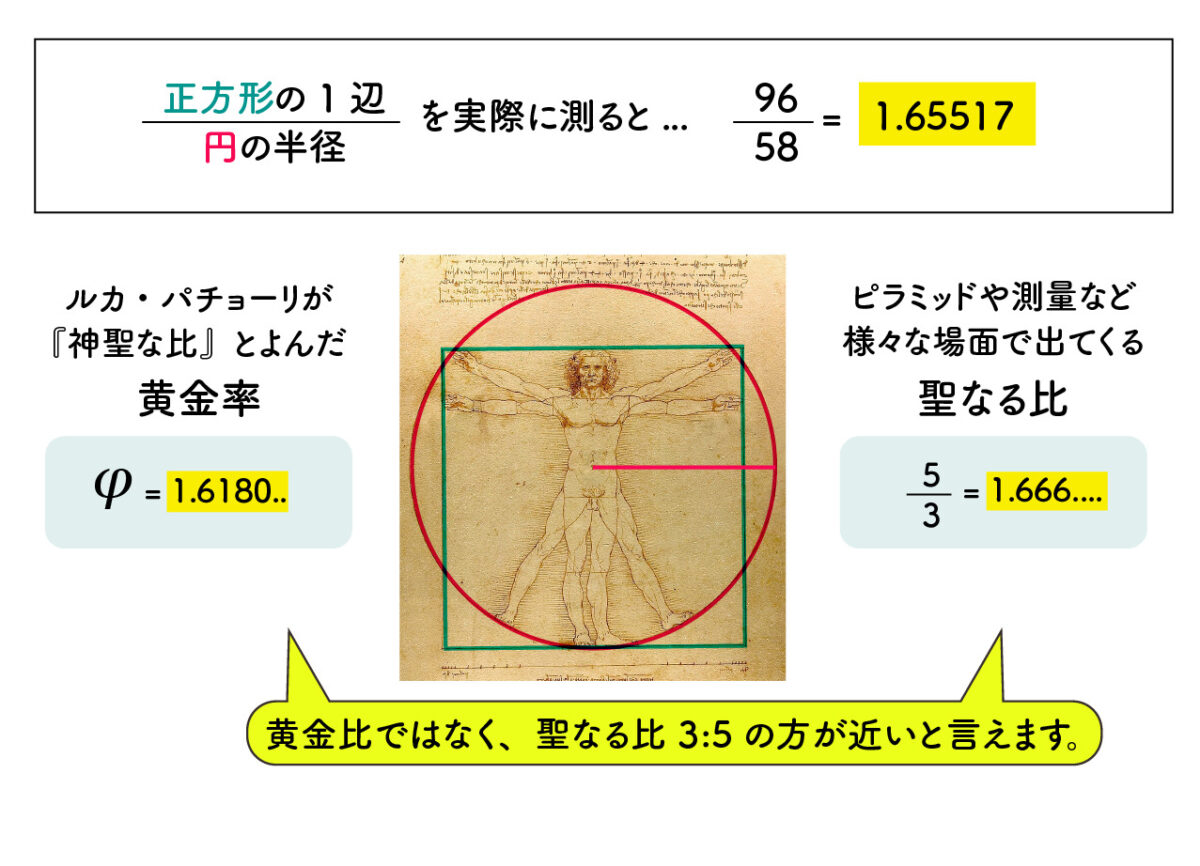
以前からこの絵の黄金比に何人かの人が疑問を持ちました。「ダ・ヴィンチは現実の人間を描写したから一致しなかった」という意見や、円の中心を臍の下にずらすなど、ウィトルウィウスの意見に従わない変形を行ったりしています。
ダ・ヴィンチは古代エジプトの単位を使っていた?!
この絵の下に「掌尺」、「寸」と書かれた目盛りが書かれています。なんとダ・ヴィンチは古代エジプトの単位を用いているのです。
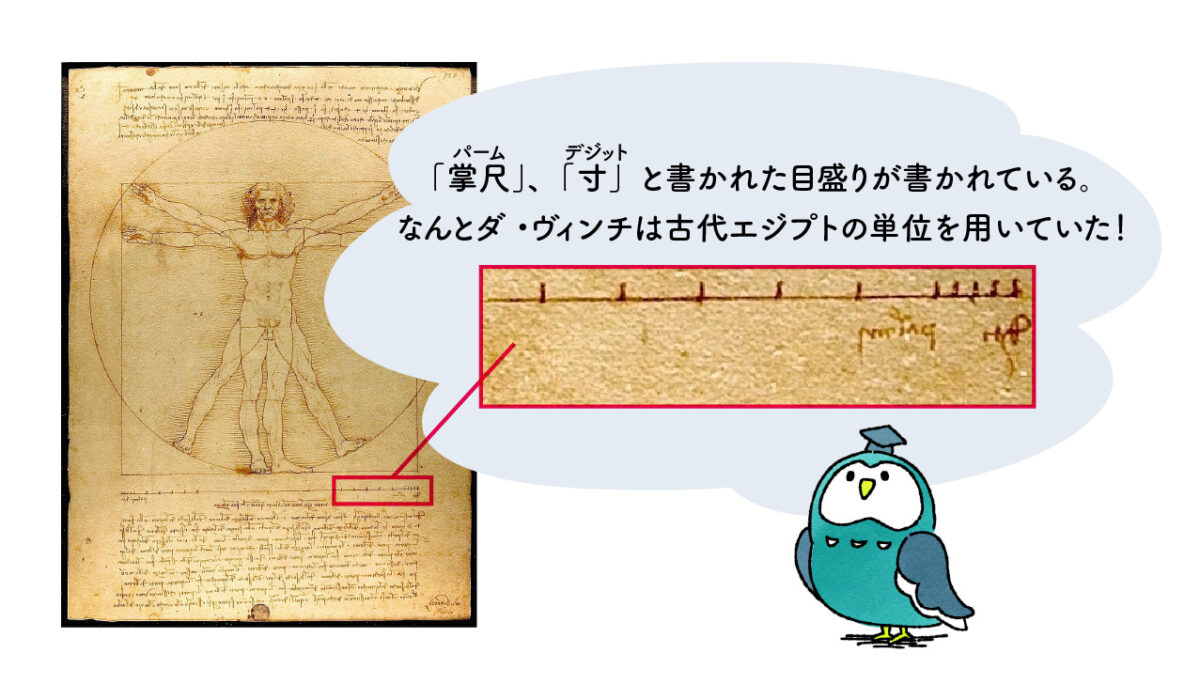
ここで使われているのは、「王家の腕尺」ではなく、「標準腕尺」です。標準腕尺では次のように定められています。
1腕尺 = 6掌尺、1掌尺 = 4寸
この図から、正方形の1辺は4腕尺です。そこで、この 3 5を計算してみます。
4腕尺×3 5
= 12 5
腕尺= 2 ; 2 5 腕尺
= 2 腕尺 2 5
×6 掌尺
= 2 腕尺2 掌尺 2 5
×4 寸
= 2 腕尺 2 掌尺1 ; 3 5
寸
最後の 3 5 寸を四捨五入すると
4腕尺 × 3 5
≒ 2 腕尺2 掌尺 2 寸 = 58 寸
となります。正方形の1辺は 4腕尺= 96寸ですから
正方形の1辺 円の半径 = 96 58 = 1.65517
となり、ぴったりと一致します。おそらくダ・ヴィンチは円の半径をこの単位を使って描いたのだと思われます。無理数を含む φ や、複雑な操作を含む幾何学的な作図を用いて円の半径を求めたのではないのです。
ここで強調しておきたいのは、はるかな時を越えて、古代エジプトで使われていた単位をルネサンス期のダ・ヴィンチが使っていたということです。エジプト文明の多くのことがらが、現在では失われてしまっていますが、かつてはヨーロッパに伝わっていたのです。印刷技術が普及するまでは、著作は筆写によるものでした。筆写には改ざんがつきものですが、それよりも取捨選択の影響の方が大きいとも言います。近世に入ると、西ヨーロッパの科学技術は長足の進歩を遂げ、オリエントを追い抜きます。そうなると遅れたエジプトの数学や科学の文献をわざわざ苦労して筆写しようとする人はいなくなったのではないかと思います。特に西ヨーロッパの人々にとって都合の悪いことがらは切り捨てられたと思います。
--Advertising--
私たちは黄金比を美しいと感じるのか
これまで多くの絵画や彫像、建築物などには黄金比が使われている言われてきました。はたして私たちは黄金比を美しいと感じるのでしょうか。私たちは生まれてこのかた毎日パターンの識別をしています。久しぶりに会った友人でもすぐに認識できます。ペンギンでさえ親は子をすぐに見分けることができるそうです。これはどのようなメカニズムによるのでしょうか。現在顔認証システムはずいぶん発展していますが、まだまだパターンの認識アルゴリズムには不明なところが多いそうです。私たちが形を認識する認知機能に黄金比が関係しているのかもしれません。
自然界にも現れるフィボナッチ数列
黄金比は人工の美術工芸だけでなく自然界にもよく現れます。前に議論したフィボナッチ数列を復習しましょう。次がフィボナッチ数列です。
1, 2, 3, 5, 8, 13, 21, …
この数列の隣り合った2 数はしだいに黄金比に近づきます。3 : 5 がこれまで述べてきた「聖なる比」ですが、5 : 8 は現代でも黄金比の近似値として用いられます。フィボナッチ数列が自然界に現れるのは、一種の「自己相似性」のためだと思われます。つまり、成長していく過程で、これまでに作ったものと相似なものを構成するようにすれば、必要な情報が節約できます。古代のエジプト人やギリシア人はフィボナッチ数列という概念を持ってはいませんでした。しかし、自然界にはフィボナッチ数列がいたるところに存在しているのです。
エジプトやギリシアには黄金比で設計されているとされる建造物や彫像が多くあります。本書では、古代の人々はこれらの建造物を「黄金比を意識して造ったのではない」と述べましたが、これは黄金比の建造物が存在しないといっているわけではありません。実際、セケド 51 2 のピラミッドはすべて黄金比の謎を満たしますし、セケド 51 4のピラミッドの「底面 : 側面」はすべて「聖なる比 3 : 5」となります。
--Advertising--
古代ギリシア人の数値扱い能力と黄金比
最後に、ウィトルウィルス的人体図には黄金比が使われていないであろうという根拠を補強しておきたいと思います。黄金比(外中比)はユークリッドの『原論』の第VI巻になってはじめて出てきます。当時のヨーロッパの人々が理解できたのは最初の第I,II巻の平面幾何だけで、第VI巻以降は難解で理解できなかったであろうと考えられています。古代ギリシア人が扱う黄金比には数値は現れません。古代ギリシアや西ヨーロッパの人々が小数や分数を扱えるようになるのは近世に入ってからです。エジプト人は分数を、バビロニア人は小数を使っており、アルキメデスは両方を使っていましたが、分数や小数はローマにも西ヨーロッパにも伝わりませんでした。ですから黄金比に関する議論で φ= 1.618 などという小数を用いるのは時代錯誤です。
ギリシアのパルテノン神殿には黄金比が使われているという話は有名です。しかし、パルテノン神殿が建設されたのは古典期が始まるころで、『原論』の「比の理論」が構築されるよりも前だと考えられます。したがって、パルテノン神殿に黄金比が使われているはずはなく、もし使われていたとしたなら、それは黄金比ではなくエジプトの「聖なる比」の可能性があります。