3-1.古代エジプトの数の扱いと単位

エジプトの分数表記とホルスの目

古代の科学について述べるときに注意しなければならないことは、古代で得られている技術や概念だけを用い、現代の概念を古代に持ち込まないことです。数学で最も基本的な概念は数です。しかし数という概念は古代と現代ではずいぶん違うのです。ヨーロッパでは、古代どころか近世になるまで数といえば自然数だけだったのです。分数とか小数はいうまでもなく、ゼロ 0 とか小数や分数は知らなかったのです。現代の皆さんは子供のころから数に慣れ親しんでいて負の数や小数などはもともと自然界に存在しているかのように思っていることでしょう。数という概念はあまりにも基本的なので、「知らなかった状態に戻れ」といわれてもなかなかできるものではありませんが、できるだけ古代人に戻って、当時の人は分数をどのように捉えていたか考えてみましょう。

分数とは、最小の単位より小さい量をはかるためのものです。最小の単位で測れないものは、「半分（二分）」、それより小さいものは「半分の半分（四分）」と測ります。世界中どんな言語でも 1 2 を表す半分という語を持っているようです。日本では1両の半分を二分金、1 4 を四分金と呼んでいました。2-4.オリシス神話で述べたようにエジプトでは、

1 2, 1 4, 1 8, 1 16, 1 32 , 1 64 (1)

のそれぞれを表す6個の記号を持っていました。図2.4.2 の「ホルスの目」参照。

×

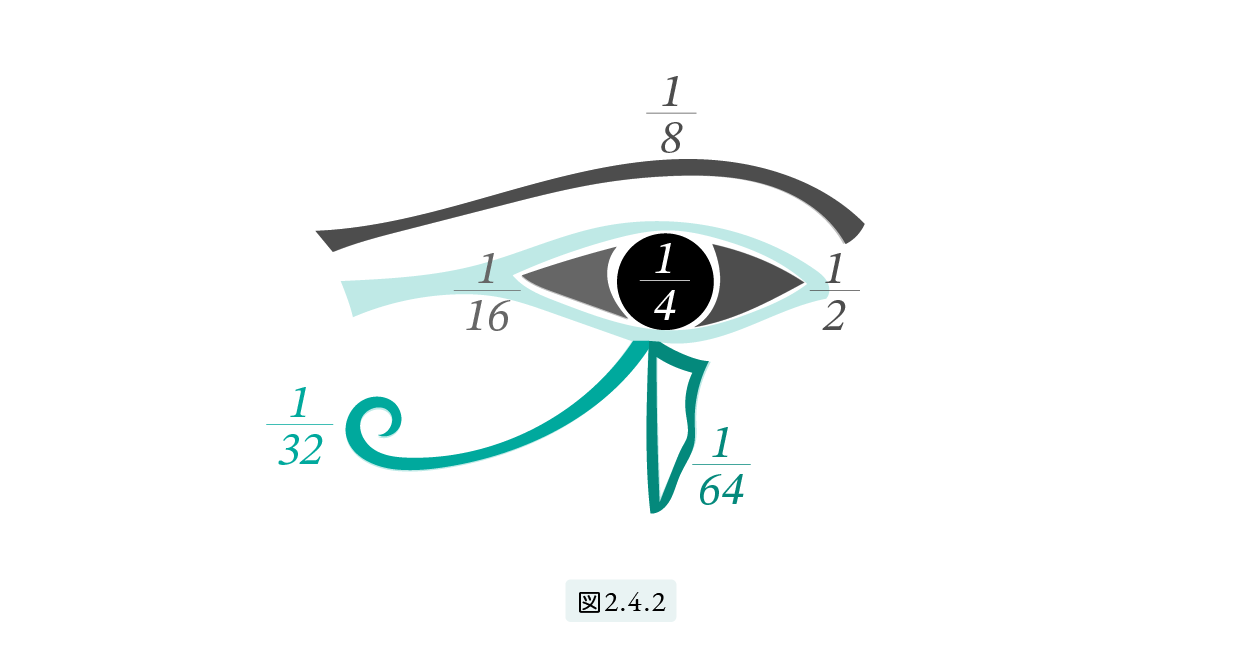
この6つの部分が図で示されるような6つの分数を表します。ホルスの目は扱いにくいし、皆さんも覚えにくいと思うので、以下では「ホルスの目」の代わりに (1) を使うことにします。ただし、たとえば 1 32 はこれで一つの記号とみてください。数と数の区切り記号としてセミコロン( ; ) を使います。したがって、

3;14;116寸デジット ＝ 3寸デジット ＋ 1 4寸デジット ＋ 1 16寸デジット ＝ 3.3125寸デジット(2)

となります。エジプトの長さの最小単位は寸デジットで、1寸デジットは約 1.8cm です。この 1 64は 0.028cm ＝ 0.28mm です。つまり、この「ホルスの目」を使えばわずか 0.3mm の長さまで表すことができるのです。古代ではこんなに小さい長さまで測る必要はなかったと思います。

2進分数と2進小数

現在のコンピュータは2進数を使っています。ここで少し2進小数について説明しましょう。これからあとは古代ではなく現代の数学の話です。上で述べた「ホルスの目」の (1) を次のように無限に拡張しましょう。

1 2¹ , 1 2² , 1 2³ , 1 2⁴ , 1 2⁵ , … (3)

ここで (3) の中から適当に有限個選んで並べたものを2進分数と呼ぶことにします。ただし、同じものを2個以上選んではいけません。たとえば

1 2¹ ; 1 2³ ;1 2⁵ ;1 2⁸ (4)

は2進分数です。2進分数は、次のようにすれば2進小数に変換できます。

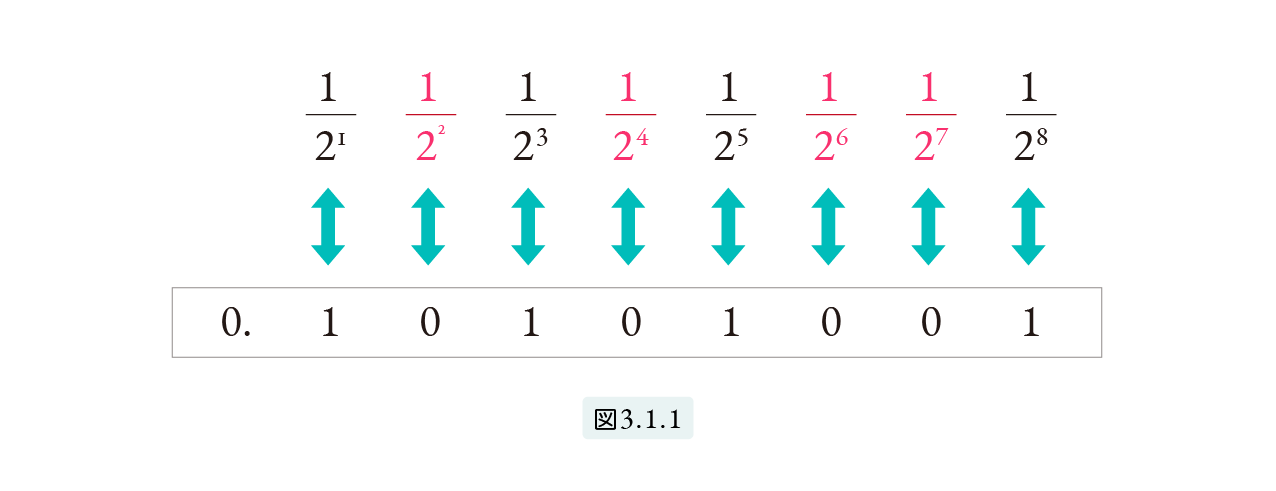
図3.1.1 で赤は現れていない分数です。1 2ⁿ が現れていれば n桁目を 1とし、現れていなければ 0 とします。このようにすれば (4) の2進分数は、2進小数

0.10101001

に変換することができます。逆の変換も同様です。2進小数のn桁目が 1 なら 1 2ⁿ を加え、0 なら加えません。

2進分数を活用した長さの精密な表現方法

ここで2進分数を使えば、任意の長さがいくらでも正確に表すことができることを示しましょう。長さが 1 より短いロープを物差しで測ることにしましょう。

▼『２進分数』を使って任意の長さを表す方法　動画説明はこちら

▼上の動画説明を再度復習しましょう。　

図3.1.2(a) のようにロープがメモリ 1 2 を越えたとします。このときは 1 2 を記録し、1 2 から 1 の部分を拡大します。実際にはこんな機能を持った計測機器はないのですが、仮にあったと仮定します。拡大すると 図(b) のようになったとします。この場合は1 4を越えていませんから 1 4 は記録しません。区間 1 2 と 1 4 の部分を拡大し図(c) となったとします。これも 1 8 を越えていません。さらに拡大し図(d)となったとします。こんどは 1 16 を越えていますから 1 16 を記録します。

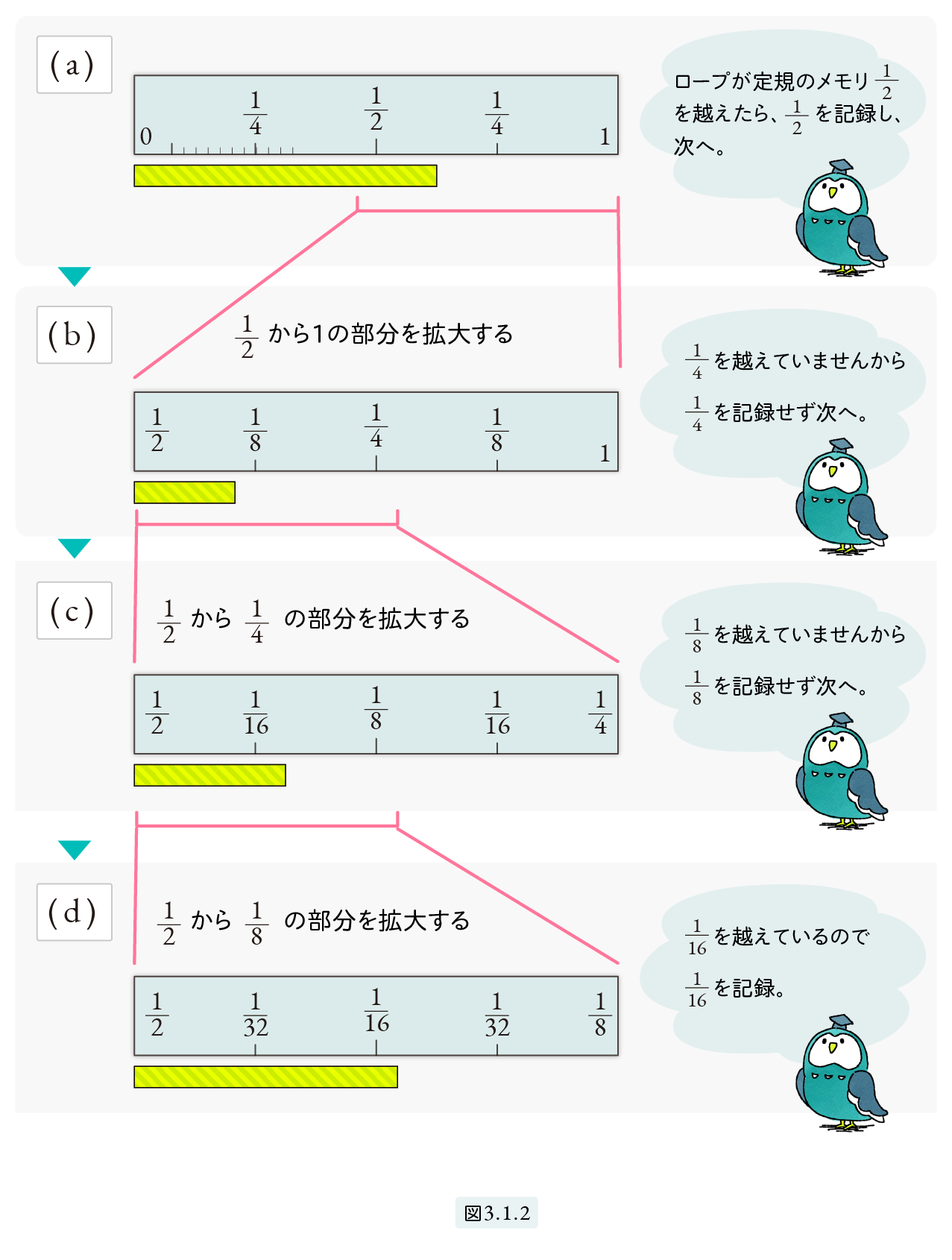
この操作はぴったりと測りきれるまでいくらでも続けることができますが、ここで中止することにします。記録したのは

1 2;1 16

でこれがロープの長さになります。測り切れなかった残りの誤差は (d) より 1 16 以下です。上で「この操作はいくらでも続けることができる」と書きましたが、これは“数学上の話”で現実には無理です。実際、1メートルのロープを 20回半分に切り分け続けることはできません。30回続けたら原子の大きさを越えて、小さくなります。

原子の大きさ > 1 10¹⁰ メートル > 1 2³⁰ メートル

エジプト分数とは

実際問題を解く場合は有限の2進数（あるいは10進数）で問題ありません。現在のコンピュータは有限の2進数しか扱っていません。しかし、円周率 π＝3.14… とか 黄金率 φ＝ 1.618… は有限の小数では表せないのです。数学を美しい体系としてまとめるには、有限の枠を越えて無限の世界に出ていかなければならなかったのです。

エジプト人は、しかし2進分数では満足できなかったようです。1 3, 1 5, … などほとんどの分数が2進分数で表すことができないからです。そこでエジプト人はエジプト分数とよばれる分数に拡張します。

分子が1で分母が自然数である分数を単位分数といいます。エジプト分数とは、自然数と単位分数の列のことです。ただし、2個以上の場合区切り記号は ; とします。また、自然数は高々1個で、同じ単位分数が現れてはいけないとします。たとえば

3;1 4;15 や　3　や 1 4

はエジプト分数ですが、

5;1 4;1 4;1 9

はエジプト分数ではありません。同じ単位分数 1 4 が現れているからです。自然数1個もエジプト分数に含めるのは現代式のやり方です。こうすれば、「自然数もエジプト分数」ですから、たとえば「エジプト分数の四則演算」などを統一的に述べることができます。

古代ではどこでも分数は単位分数が基本でした。私たちは分数m n を「n分ぶんのm」と呼んでいます。この「n分」とは「n等分した1個」のこと、つまり単位分数を意味します。したがって、「n分ぶんのm」は、「n等分したものがm個」の意味です。

エジプト分数の具体例：2枚のパイを7人で分ける

エジプト分数は、現在の分数に比べ扱いづらく欠点が多いのですが、エジプト分数にはそれなりの理由もあります。たとえば、2枚のパイを7人で分けることを考えます。2 7 は分子が 2 ですからエジプト分数ではありません。これは次のようにしてエジプト分数に変換できます。

2 7 = 2 × 4 7 × 4 = 7 + 1 7 × 4 = 1 4 + 1 28 = 1 4;1 28

2枚のパイのそれぞれを4等分すると、1 4のパイが 8 個できます。そのうちの7個を7人に分けます。残った 1 4のパイを 7 等分すると 1 28のパイが 7 個できます。したがって、1人の取り分は、1 4 と 1 28となります。一般に、2 7 のような単位分数でない分数は、大きさがすぐには分かりにくいものです。しかし、1 4 は単位分数だから、直感的にわかります。2 7 はだいたい 1 4 と残りは小さな 1 28 です。

本連載では、エジプト分数の細かな議論はしません。しかしエジプト人は私たちが分数を扱うのとほとんど同等の能力で複雑な計算問題や応用問題を解いていました。

2進分数はホルスの目の部分で表記していました。では一般のエジプト分数はどのように表記していたのでしょうか。その前にまず一般の自然数について見てみましょう。エジプト分数は古代としてはとても進んだ数体系ですが、古代の進歩は非常にゆるやかですから、数字が最初に書かれてからエジプト分数が現れるまでには何百年もの年月が経っていたんだと思います。

古代の記数法

線刻とは何か：棒を使った数の表現

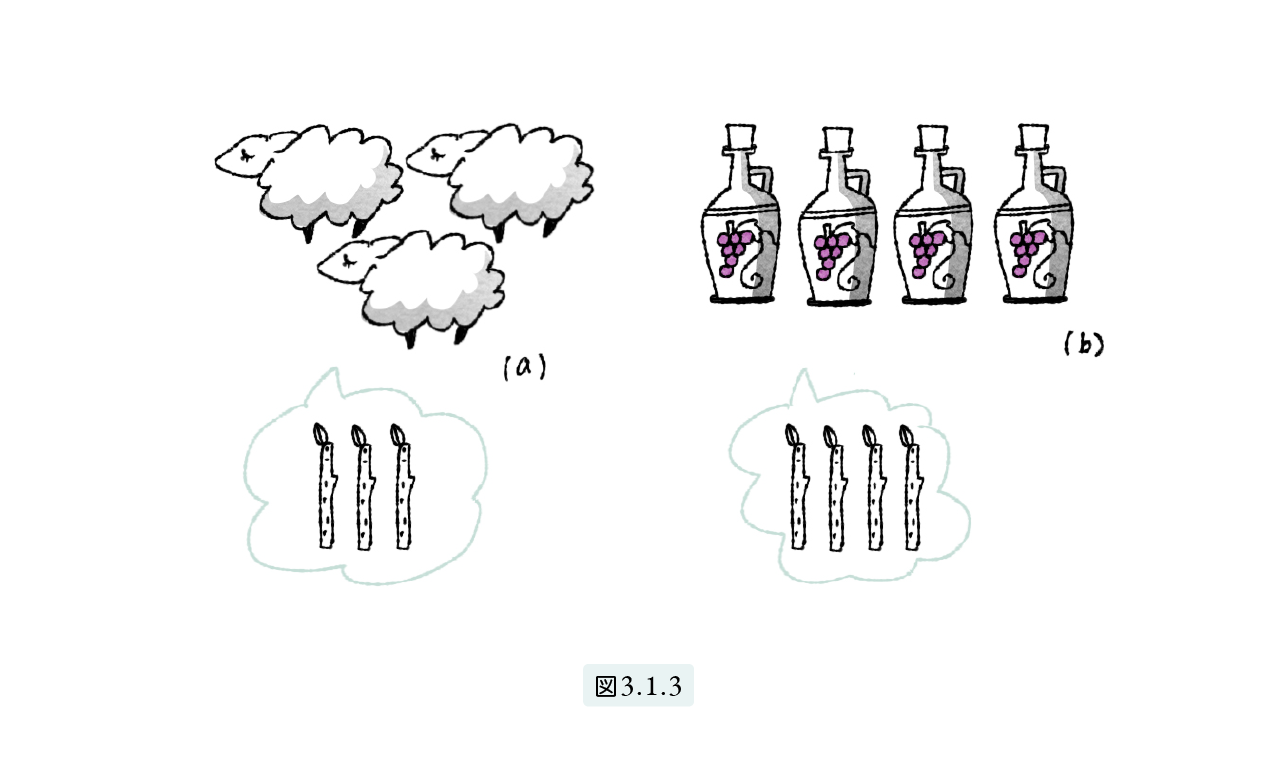
記号を使って、数を表す方法を記数法といいます。数のなかで最初に使われるようになったのは個数を表す自然数です。最初は、たとえばヒツジ3頭を表すには、図3.1.3(a) のようにヒツジの絵を3つ、ワイン4壺を表すには 図 (b) のように壺を4つ書きました。しばらくして、羊を数えるときも、人数を数えるときも、日数を数えるときも同じ小枝が使えることに気が付きます。これは“大発見”です。だとしたら、ヒツジや壺の絵でなくても棒で十分です。

棒で数を表すことを線刻といいます。石器時代は獣の骨に刻まれましたが、普通は木片に刻まれました。1-2.エジプト数学と歴史観の変遷で述べたローマ数字を見てみましょう。ローマ数字では 1 は I で表されます。十を表す X は I の10個の束を表していて、斜め線 / は束たば を束ねた紐です。V は X の上半分で、10の半分の5を表します。つまり、数字の X や V はアルファベットの文字ではなく線刻だったのです。私たちの漢字を見てみましょう。十は 1 の10個の束、廿にじゅうは十が2つ、丗さんじゅうは十が3つです。どこの国でも 1, 2, 3 は同じように書かれたようです。2 と 3 は、図3.1.4 のように 二と三を続けて書いた形からきているようです。

線刻は木または竹の繊維を切るように刻まれました。中国（日本）の 一、二、三の線が横向きなのは、竹に刻まれた |, ||, ||| を縦にして上から下へと読んだからのようです。

エジプトの記数法は10進法で、図3.1.5で示される文字（数字）を用います。たとえば蓮の花は千を、カタツムリは百を表します。

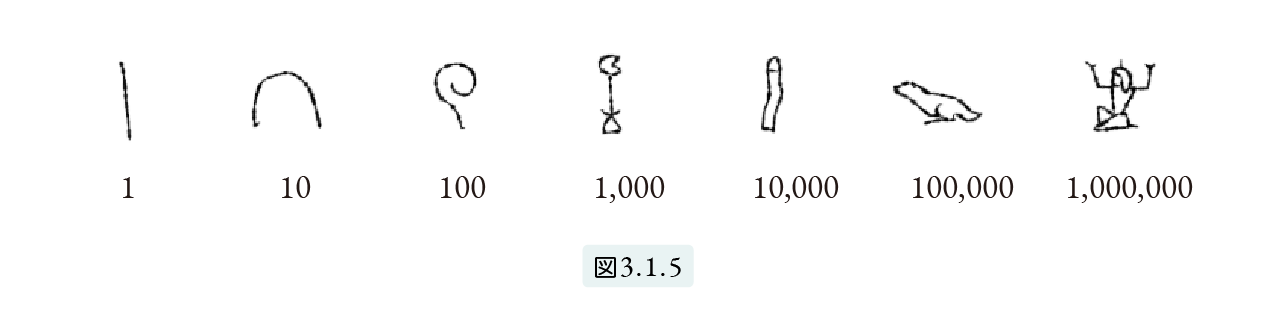
したがって 2,123,013 は

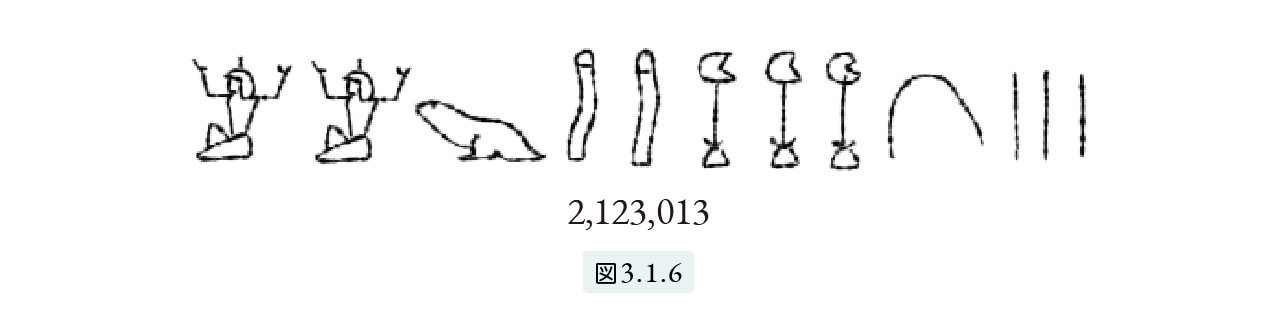
と書きました。

エジプト分数：ホルスの目を使った表現

単位分数 1 n は、n を表す表現の上に“ホルスの目”を表す記号を書いて示しました。たとえば 1 3 と 1 5 と 1 32 は図 3.1.7 のように表しました。エジプト分数が私たちの使っている分数に発展することなく、エジプト分数のまま留まったのは、このような表記法に原因の一つがあるのかもしれません。

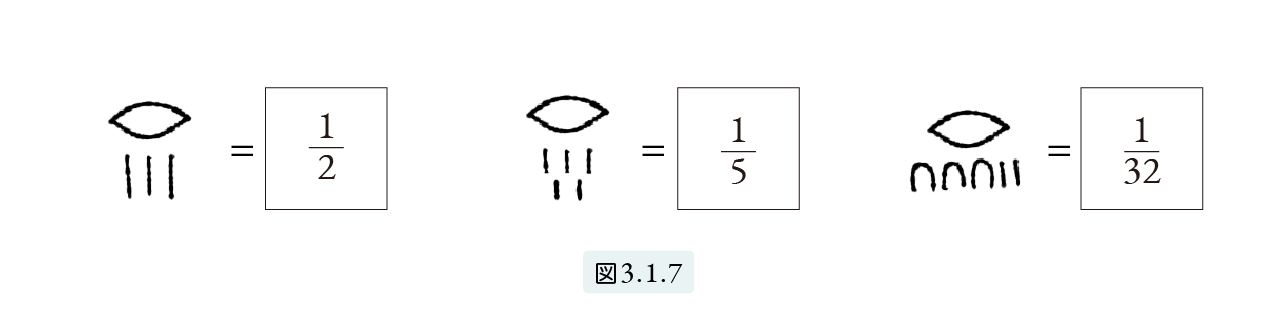
個数を表す自然数は、数える対象から引き離され、独立した抽象的な存在として認識されるようになります。たとえば図3.1.6 でエジプト人が表す数は、現代の私たちが頭に描く 2,123,013 という数と同じものを示しています。これらの表記が表すものは数える対象（たとえばヒツジとか壺）とは独立した“自然数”という抽象的な対象なのです。それでは個数以外の、長さ、面積、体積、角度などはどのように認識されていたのでしょうか。古代人がどのように認識していたか、具体的には分かりませんので、現象面だけを見ることにします。

エジプトの長さの単位：腕尺(キュビット)・掌尺(パーム)・寸(デジット)

エジプトの長さを復習しましょう。1-3.ピラミッドの謎に魅かれた人たちで述べたように、長さは

1腕尺キュビット＝ 7掌尺パーム、1掌尺パーム ＝ 4寸デジット

という単位で表されます。ここで 1, 4, 7 などは現在の算用数字を使っていますが、これらはエジプト文字で書かれていると考えてください。すると、たとえばある長さは

2腕尺キュビット5掌尺パーム 3寸デジット (4)

と表されます。腕尺キュビットはもともとは腕、掌尺パームは掌、寸デジットは指という意味でした。したがって (4) は「腕2本、手のひら5つ、指3本の長さ」という意味です。しかしこれらは長さを表す単位に変化していきます。単位を表す名詞は数詞をともなってはじめて意味を持つ「文の構成素」となるものであり、数と単位を切り離すことはできません。

量とは単位付きの数の概念

“数”に対して“量”という概念があります。量という概念は現在でも物理などで使われていますが、数と同様時代によってまた人によっても意味が違うことがあります。本連載では、

量とは単位付きの数

のことを意味します。たとえば次が量です。

3日、3人、3.14グラム、22 7メートル

“数”は現在の皆さんが知っている数のことで、小数や分数を含みます。量にはいろいろな種類のものがあって、同じ種類のものしか足せないことに注意してください。たとえば重さ（グラム）と長さ（メートル）は足せません。

古代における個数以外の、長さ、面積、体積、重さ、角度、… などは、この“量”として解釈すると分かりやすいと思います。量という概念は、いろいろな単位を含む量の計算にとても便利です。上で述べたエジプトの長さの足し算を演習問題としてやってみましょう。

3腕尺キュビット 4掌尺パーム 1寸デジット ＋ 2腕尺キュビット 5掌尺パーム 3寸デジット ＝ 5腕尺キュビット 9掌尺パーム 4寸デジット＝ 6腕尺キュビット 3掌尺パーム

腕尺キュビットを掌尺パームに変換するには7倍、掌尺パームを腕尺キュビットに変換するには17 します。

6腕尺キュビット 2掌尺パーム ＝ 44掌尺パーム ＝ 6;2 7 腕尺キュビット

角度とピラミッドの解析における現代数学の適用

つぎに角度について述べましょう。円1周を 360度とする角度の単位はバビロニアでは使われていましたが、古王国時代のエジプトには伝わっていなかったと考えられています。したがって本連載でこの角度の単位を用いているときは「現代数学を使っている」と思ってください。あとで、ピラミッドの傾斜角などはこの角度を用いて現代数学を使って解析します。

1度より小さい単位は次の分と秒を使います。

1分 ＝ 1 60 度、　1秒 ＝ 1 60 分

度を分に直すときは 60倍、分を秒に直すときも 60倍します。

3度4分 ＝ 3×60＋4 分 ＝ 184分
3度4分5秒 ＝ 184 分 5秒 ＝ 184×60＋5 秒 ＝ 11045 秒

秒を分に直すときは 1 60倍、分を度に直すときも 1 60倍します。分数の代わりに小数を用いることもあります。特に断らない限り本書では、小数点表示は10進数を表すものとします。

3度4分5秒 ＝ 3度 (4＋5 60)分 ＝ 3＋(4＋5 60)×160度 ＝ 3.06855… 度

小数点表示（10進数）の“度表示”を“度分秒表示”に直すには、上で述べた「度を分になおす、分を秒になおす」を使います。

3.068055度 ＝ 3度 0.068055度 ＝ 3度 0.068055×60分 ＝ 3度 4.0833分 ＝ 3度 4分 0.0833分 ＝ 3度 4分 0.0833×60秒 ＝ 3度 4分 4.998秒

上で計算した「3.06855… 秒」の … の部分を切り捨てましたから、答えはぴったりとは一致しませんでしたが、だいたい元に戻りました。

まとめ

現在の私たちは、長さはメートル、重さはグラム、といったように量の種類ごとに単一の単位名を使っています。したがって、量を数値とみなすことになんの抵抗もありません。あるいは上で述べたように「量＝数＋単位」といった単純な図式で理解できます。しかしエジプトでは、たとえば長さに関しては、腕尺キュビット、掌尺パーム、寸デジットと違った単位の和で表されます。さらにまた、寸デジットから掌尺パーム、掌尺パームから腕尺キュビット、といった「位上がり」は10進ではありません。こういったことも、「長さも数の一種である」といった見方を阻んでいたのかもしれません。