ピラミッドの秘密
エジプトの歴史と神話
エジプトの数学能力
ギリシアの数
ピラミッドの謎を解く
3-3.面積の計算
ページ目次
エジプト人の面積計算法―古代数学の精巧さと創造性
歴史の父ヘロドトス※は、

ギリシア人は数学をエジプト人から学んだ
と述べています。しかしヨーロッパの人たちは長い間この言葉を無視してきました。「ピラミッドの建設にはごく初歩的な数学しか使われていない」とか、「エジプト分数は奇妙で原始的な分数だ」などと、エジプト分数※をことさら軽視する発言が多かったように思います。古代エジプトに高度な数学が発達していたことが分かってきたのは最近のことです。前節ではエジプト人が相当面倒な比の問題を解いていることを見ました。今回はエジプト人が面積をどのように計算したかを見てみましょう。
古代エジプトの実用数学と土地測量
エジプトの幾何学は、ナイル川の氾濫後の土地を測量して耕作地を農民に分配するために生まれ、一般に数学は、生産物の集積およびその再分配や、ピラミッドの建設に必要な石材量の計算などの実用数学から発達したと考えられています。前節と同様に、この節でもパピルスにあった問題を解いてみます。これらの問題を現在のメートル法の単位で置き換えると、皆さんにとっては初等的で簡単な問題だと思えるかもしれません。しかし、ここでは当時の単位を使って考えてみます。これは古代人が数をどのように考えていたか、数という概念や面積という概念をどのようにして獲得してきたかを見るためです。
古代エジプトの測量単位と農地面積の計算方法
『3-1.古代エジプトの数の扱いと単位』で述べたように、長さの単位は、腕尺、掌尺、寸でしたが、以下ではさらに次の棒尺という単位を付け加えます。
1棒尺 = 100 腕尺= 約50メートル、 (1 腕尺 = 約 0.5 メートル)
日本でも昔、検地で田畑を測るときは長い竹竿を使ったようです。ロープだと曲がったりたるんだりするようです。1棒尺 = 約50メートルですから、一度には測れず、何回かで測ったのでしょう。面積の単位は次のようになっています。
1 帯地 = 1 腕尺 × 1 棒尺 = 100平方 腕尺
1農地 = 100帯地 = 10,000平方腕尺 = 1平方棒尺
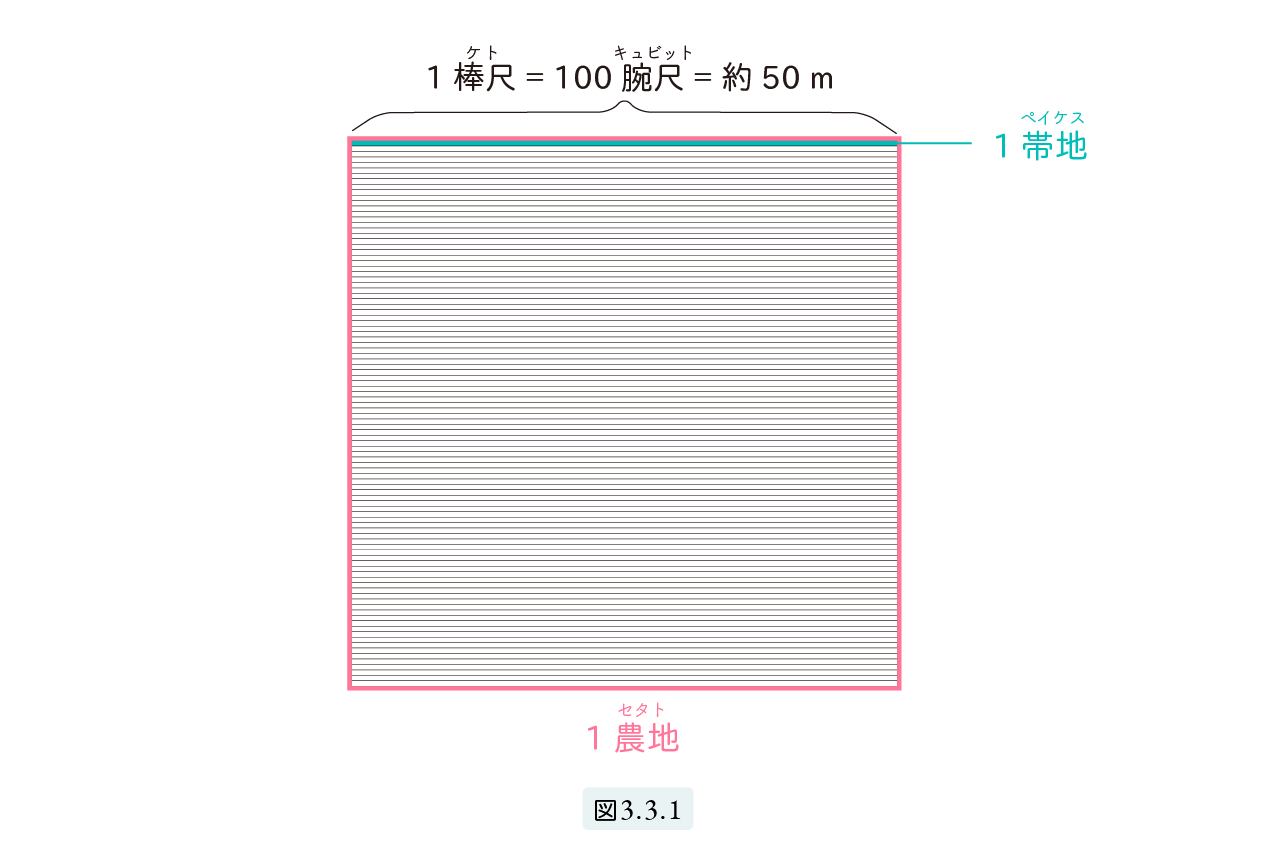
面積は縦 1 腕尺 横100腕尺の細長い帯状の面積を単位としていました。これを1帯地 といいます。畑は縄師によって横の長さが100腕尺 = 1 棒尺 の長方形に区切られていました。したがって縦の長さを測るだけで畑の面積が分かるようになっていました。図3.3.1参照。
縦の長さが n腕尺 なら、帯地が n個の n帯地となります。帯地が100個で1農地 です。つまり面積も一種の個数でした。直感的にも理解しやすく、実際に農地を計測したり、分配したりするにはとても便利だと思いますが、このような体系で
長方形の面積=縦の長さ×横の長さ (1)
という公式にたどりつくまでには長い道のりがあっただろうと思います。特に棒尺 、腕尺 、掌尺 寸などの単位が混じった長さどうしの掛け算は、計算するだけでも大変だと思います。
現在の皆さんは何の疑問もなく (1) を公式として受け入れていると思います。それはそれでまったく構わないのですが、ここで少し掛け算の生い立ちについて考えてみましょう。
面積計算の基礎としての小長方形の利用
掛け算は足し算の拡張として生まれたのだと思います。数 a の n倍、すなわち n×a は「a をn個足したもの」でした。上で述べたように、畑の面積は帯地がいくつかで測っています。エジプト人は数を自然数から分数に拡張しました。長さが分数で表わされたとき、(1) はどのように理解したのでしょうか。エジプトの単位系は複雑だから、現在のメートルで考えることにします。たとえば縦 2 3メートル、横 3 5メートルの土地の面積を考えましょう。
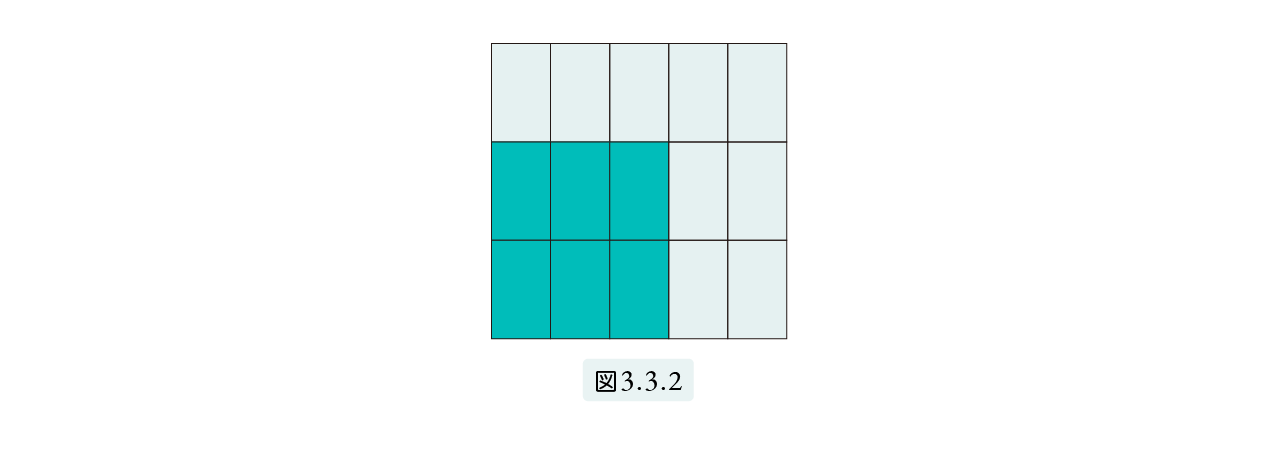
図3.3.2 のように縦横1メートルの正方形の土地を、縦を3等分、横を5等分すると、縦1 3 メートル、横 1 5 メートルの小さい長方形が 3 × 5 = 15 個できます。この小さい長方形は単位正方形(1平方メートル)の 15分の1です。縦 2 3メートル、横 3 5メートルの長方形には、この小長方形が2 × 3 = 6 個あります。したがって、影の部分の面積は 6 15 = 2×3 3×5m2 となります。縦と横の長さが一般の分数の場合も、同様の方法で一般化できます。エジプト人も、具体的な数値でいろいろな問題を解くうちに (1) が成立すると考えるようになったのだと思われます。
以下では、長さの単位は棒尺、面積の単位は農地だけとします。
1農地 =1平方 棒尺 = 1 棒尺2
であることに注意してください。棒尺2 は「平方棒尺」の略記法で現代式の記法です。パピルスにあらわれる問題を見ていきましょう。
古代エジプトの面積の問題を解いてみよう
問題3.3.1 縦の長さが横の長さの 1 2 ; 1 4 で、面積が12農地の長方形の土地がある。縦と横の長さを求めよ。注:農地 = 棒尺2
まず現代式に方程式を使って解きましょう。1辺が x棒尺の正方形の土地を考えます。エジプト分数 1 2;1 4 を普通の分数に直すと 3 4 となります。横x棒尺 、縦3 4x棒尺の長方形の面積が 12 棒尺2 ですから、方程式に直すと
3 4 x2 = 12 (2)
となります。x に関する2次方程式です。皆さんならこれを
x2 = 12 × 4 3 = 4 × 4
と変形できます。つまり、3 4 の逆数 4 3 を (2) の両辺に掛けて解きます。
エジプト人は方程式など知りませんから、おそらく次のようにして解いたと思われます。縦の長さは 1 2 ; 1 4 ですから、図3.3.3 のように、まず半分に分け、さらに半分に分けます。影の長方形は正方形の 3 4 です。

正方形の 3 4 = 長方形 (3)
また、図から明らかなように、正方形は長方形の 1 3 を4倍したものです。
長方形の 4 3 = 正方形 (4)
この (3) と (4) の式を比較すると、3 4 の“逆数”が 4 3 であることが分かります。実際エジプト人は正方形の面積を 12 × 4 3= 16 と計算しています。したがって正方形の一辺 x は 4 となります。
現在の私たちは、分数の逆数は、分子と分母をひっくり返すことで計算できますが、エジプト分数の場合は少し面倒です。しかしエジプト人は、具体的な問題を繰り返すうちに「逆数」という概念を思いつき、計算方法を習得していきました。このように、具体的ないくつかの例から一般的な法則を得る方法を帰納的方法といいます。
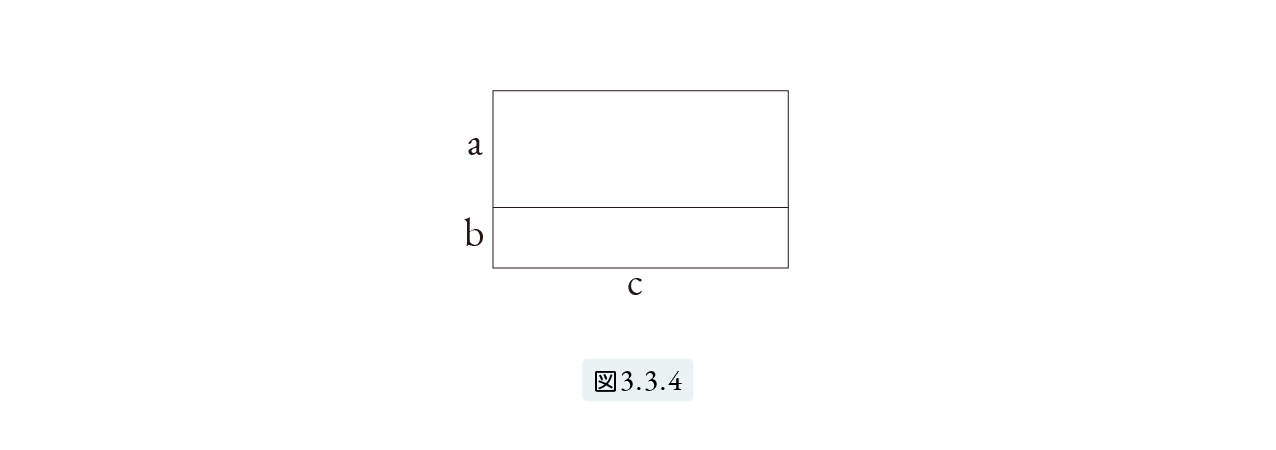
図3.3.4において、c = 1 棒尺とすると、
a 帯地 + b 帯地 = (a+b)帯地
となります。エジプト人は、c を1棒尺に制限する必要がないことに気がつきます。また、棒尺とか帯地といった単位にとらわれることなく、数 a, b, c に対して次が成り立つことに気がついたと思います。
( a + b ) × c = a × c + b × c (5)
この法則をさらに一般化して次が得られたのだと思います。
「横の長さが等しい2つの長方形の面積は縦の長さに比例する」
もちろん、エジプト人はこのような式は使えませんし、このような法則が成り立つといったようなことはどこにも書かれていません。しかしこのことは、エジプト人が残したパピルスに書かれた計算の中でこの法則が頻繁に使われていることから分かります。
古代エジプトの円の面積の扱い
ピラミッドの謎には円周率が関係していますから、次に円の面積を考えましょう。出土したパピルスには、図3.3.5のような、1辺が3の正方形の4隅の角を切ってできる八角形と円が描かれていました。
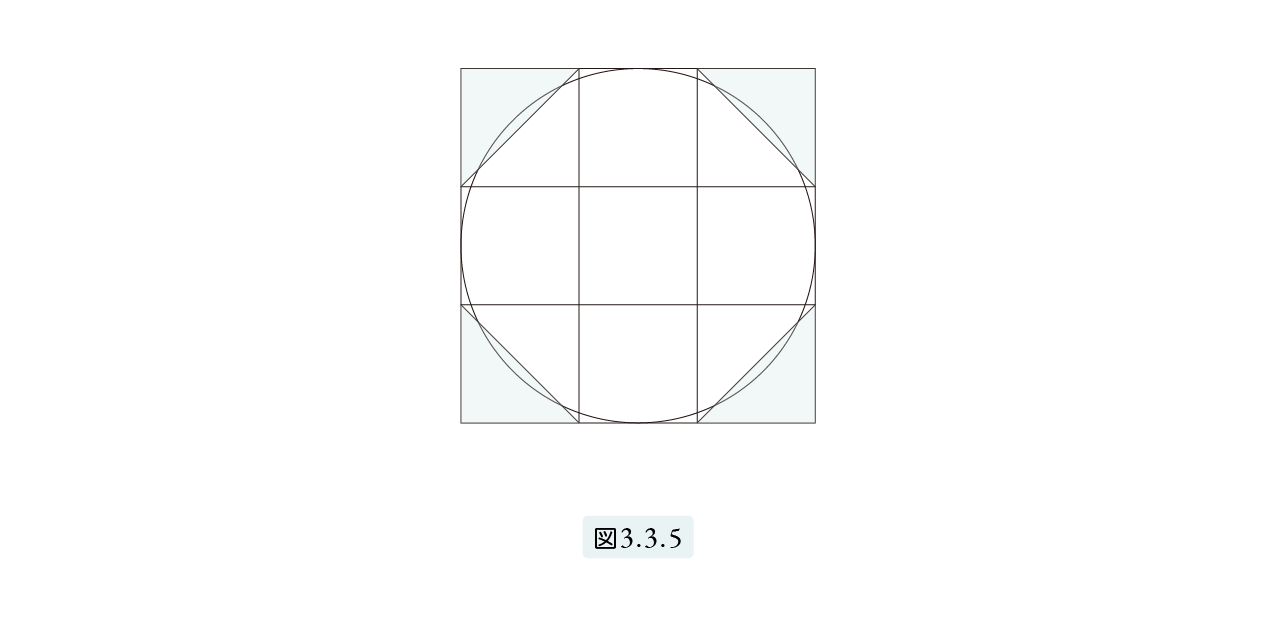
この八角形と円の面積がほぼ等しいことから、この図は円の面積を表すものだと考えられています。計算しやすいように、正方形の1辺を3ではなく9としましょう。すると、八角形の面積は、正方形の面積 81から影の部分の面積 18 を引いた 63 となります。
エジプト人はこれをもっと計算しやすい 64= 82 としました。つまり、
直径 9 の円の面積 = 1辺が8 の正方形の面積。
としたのです。図3.3.6の直径9の円と 8 × 8 の正方形を比べてみてください。
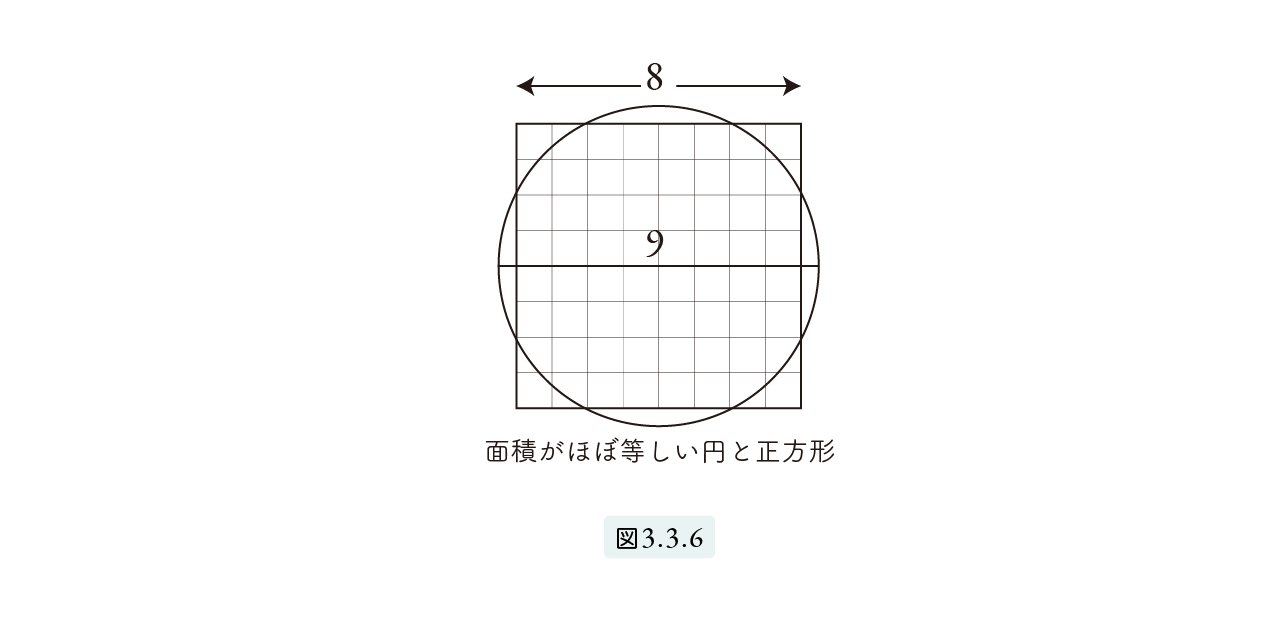
問題3.3.2 直径が9棒尺の円形の土地の面積はいくらか。
パピルスでは、この土地の面積を次のように計算すると述べています。直径9からその1/9を取り去ると残りは8。8を8倍すると64。したがって面積は 64棒尺2 = 64農地でとなります。つまり書記が述べていることは、
円の面積 = (直径×8 9)2 (6)
で計算できる、ということです。現代の皆さんのために、半径 r で書き直すと面積 S は
S = (2r×8 9)2 = 256 81 r2
で求められるということです。 256 81 = 3.160 …ですから、πのきわめてよい近似といえます。誤差はたったの 0.6パーセントです。
古代エジプト人は円の性質をどこまで知っていたか
エジプト人は円の面積は外接する正方形の面積の 約64 81倍であることを知っていました。すなわち、円の面積が外接する正方形の面積に比例することを認識していたのです。したがって実質的に比の概念を知っていたとみてよいでしょう。また (6) は、面積に対する公式であって、円周に対する公式ではありません。
「円周が直径に比例すること」と「円の面積が外接正方形の面積に比例すること」を数学的に証明したのはギリシア人であり、この2つの比の値が一致することを証明したのはアルキメデス※です。これについてはChapter4で述べます。
元祖ピタゴラスの3つ組
次を満たす3つの自然数 a, b, c をピタゴラスの3つ組といいます。
c2 = a2 + b2
もちろん、ピタゴラスはピラミッドの時代より千年以上も後の人です。(a, b, c) がピタゴラスの3つ組なら、(a, b, c) を3辺とする三角形は直角三角形となります。もっとも小さいピタゴラスの3つ組は (3, 4, 5) でこれを元祖ピタゴラスの3つ組と呼ぶ人もいます。
問題3.3.3 2つの正方形の土地 A と B がある。B の1辺は A の1辺の 2分の1と4分の1である。2つの土地を合わせると 100農地である。2つの正方形を求めよ。
A の1辺を x棒尺とおいて方程式で解いてみましょう。B の 1辺は (3 4)x ですから、
{1+(3 4)2 } x2= 100
となります。
現代では誰が解いてもほとんど同じ方法になると思いますが、古代の数学ではいろいろな解き方があります。ここでは“仮定法”と呼ばれる方法で解いてみましょう。A の1辺を 4棒尺と仮定します。なぜ 4 にしたかというと、B の1辺が簡単に計算できるからです。B の1辺は 3 となります。すると A と B の和は 42 + 32 = 25 となります。
しかし実際は 25 ではなく 100 でなくてはなりません。A と B の和を4倍にしなければなりません。和を4倍ということは、A を4倍、Bも4倍ということです。エジプト人は「辺が2倍になれば面積は4倍になる」ことを知っていたようです。したがって、A と B の辺をそれぞれ2倍し、A の1辺は 8棒尺、B の1辺は 6棒尺となります。
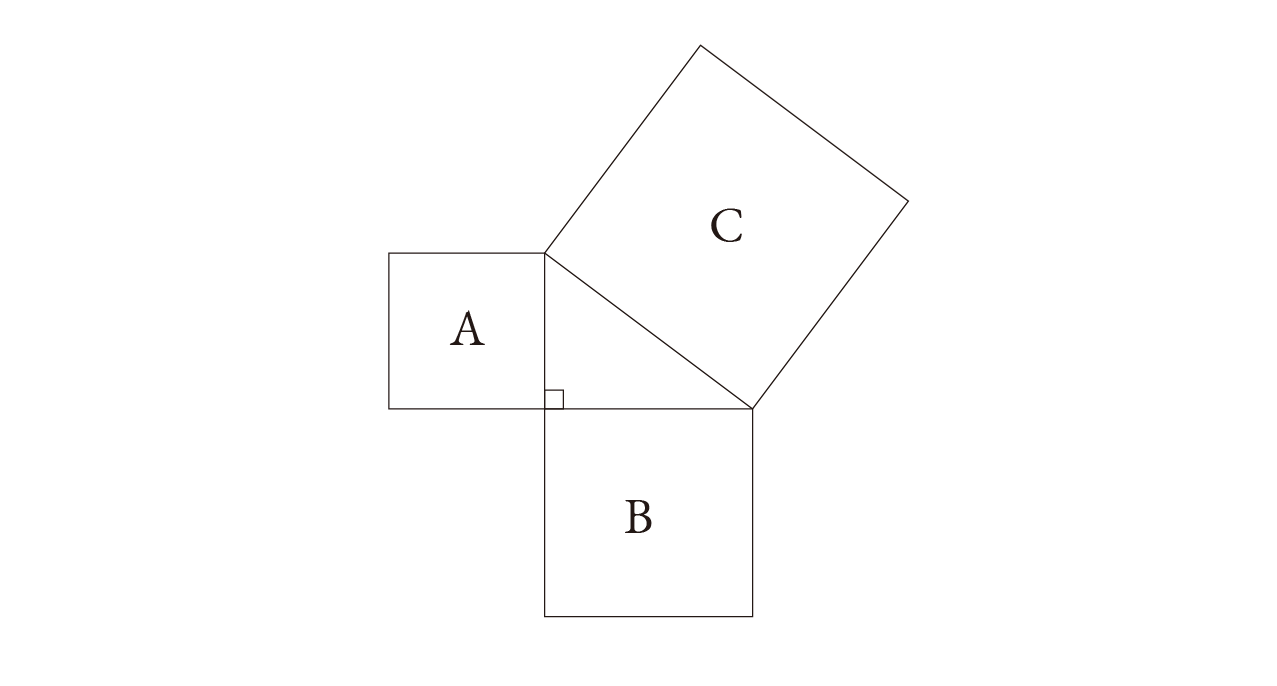
問題3.3.3の答えに注目してください。A = 82 , B = 62 , A+B = 102 となっています。6, 8, 10 をそれぞれ 2 で割ると 3, 4, 5 となります。(3, 4, 5) は元祖ピタゴラスの3つ組であることに注意してください。またこの問題は、2つの正方形の面積の和を計算していて、和も正方形の土地となっています。
現在の所、エジプト人がピタゴラスの定理を知っていたという証拠は見つかっていません。しかし、(3, 4, 5) がピタゴラスの三つ組であること、つまり 32 + 42 = 52 となることは分かっていました。またこの問題が2つの正方形 A と B の和が正方形 C となることを扱っていることより、この三つ組に対しては図で示されるようなピタゴラスの定理が成り立つことを知っていたような気がします。証拠にはなりませんが。