黄金比 〜五芒星に現われる美しい比率〜

黄金比とは

人間が最も美しいと感じる比率とされてる黄金比。美術や商業デザインにも取り入れられることが多く、皆さんも一度は「黄金比」という言葉を耳にしたことがあるのではないでしょうか。そもそも黄金比とはどのようなものなのでしょうか。

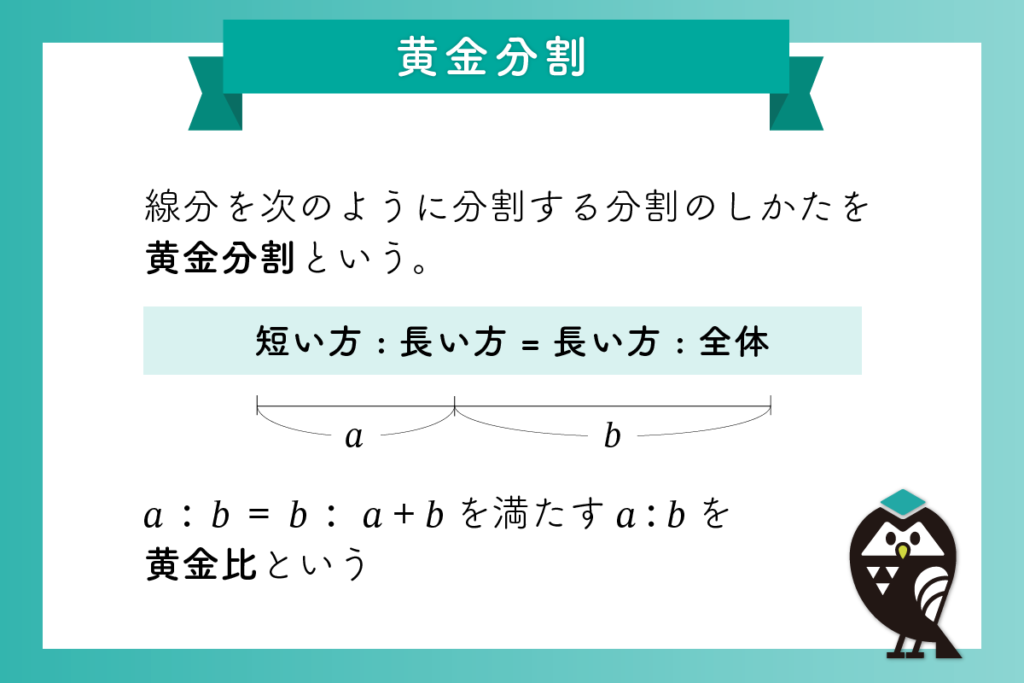
線分 AB を点 C で2 つに分割します（図1）。AC が CB より短いとします。ACの長さを a、CB の長さを b とします。線分 AB を次を満たすように点 Cで分割する分割のしかたを黄金分割 といいます。

短い方 : 長い方 = 長い方 : 全体

式で表すと以下のようになります。

a : b = b : a + b　　　　　　　　　　　( 1 )

( 1 ) を満たすa : b を黄金比といい、b / aを黄金率と呼びます。（ b / a の逆数 a / b を黄金率と呼ぶこともあります。）黄金率はよくギリシア文字 φふぁいで表されます。

黄金比の計算

( 1 ) に外積の項・内積の項の積の公式を使うと

b² = a × ( a + b )　　　　　　　　　　( 2 )　

となります。( 2 ) の両辺を a²  で割り、x = b / a とおくと、次の二次方程式が得られます。

x²  = 1 + x　　　　　　　　　　　　　( 3 )

この二次方程式 ( 3 ) の正の解は

φ = ( 1 + √5 ) / 2 = 1.6180339887…　 ( 4 )

となります。この φ が黄金率で、1 : φ が黄金比です。

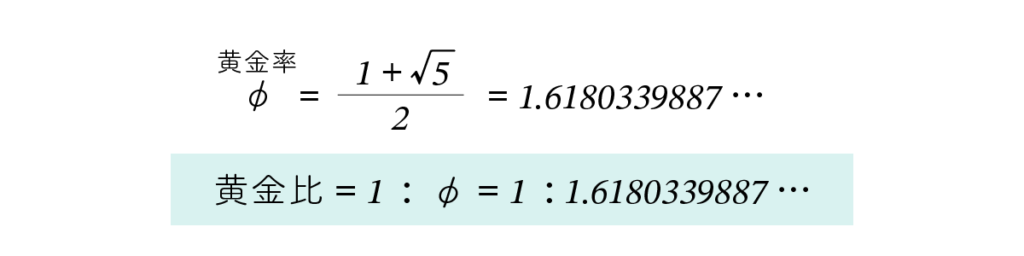
黄金比とフィボナッチ数列の関係

〔フィボナッチ数列とは？〜自然界にも存在する不思議な数列〜〕でフィボナッチ数列の隣り合った数の比は、黄金比の近似値になっていると述べました。フィボナッチ数列の隣り合う数の比を計算して確かめてみましょう。フィボナッチ数列は以下のような数列です。

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

隣り合う数の比 1/1, 2/1, 3/2, 5/3, 8/5 , …を計算して並べると、次のようになります。

1, 2, 1.5, 1.66…, 1.6, 1.625, 1.615…, 1.619…,

このように、フィボナッチ数列の隣り合う2項の比は( 4 )で得られた黄金率φに収束しそうです。

ギリシア数学における比とは

ギリシア数学の特徴の一つは“ 比” であり、その中でも今回のテーマである黄金比は特に有名です。黄金比という言葉は近世になってできた言葉で、ギリシア幾何学では外中比と呼ばれていました。

ギリシアの「幾何学」は定規とコンパスだけで行うもので、数値は現れません。これは「禁止されている」というのではなく、そもそも前提となる概念のなかに数値が含まれていないのです。「幾何学」ではまず使ってもよい概念を公理や定義として述べてから理論を展開します。この方式はギリシア以降数学の標準として踏襲されてきます。ギリシアの幾何学では比はどのように扱われいたのでしょうか。

古代ギリシア人にとって、比 a : bとは2 つの量 a と b の間の“ 関係” を表わすものであって、 b / a という一つの対象（数値）を表わすものではありませんでした。
また、φ のような無理数は古代には存在しません。これらが数として扱われるようになったのはやっと近世に入ってからです。φ＝1.618… という数値が使えないとしたら、黄金比はどのように扱われていたのでしょうか。ギリシア幾何学によく出てくる五芒星を見てみましょう。

五芒星と黄金比

図2-(a) のような星形を五芒星（ペンタグラム）といいます。ピタゴラス学派は五芒星を教団のシンボルとしてとても大切にしていました。五芒星の中には黄金比が現れます。五芒星の各頂点を結ぶと図2-(b)のような正五角形となります。

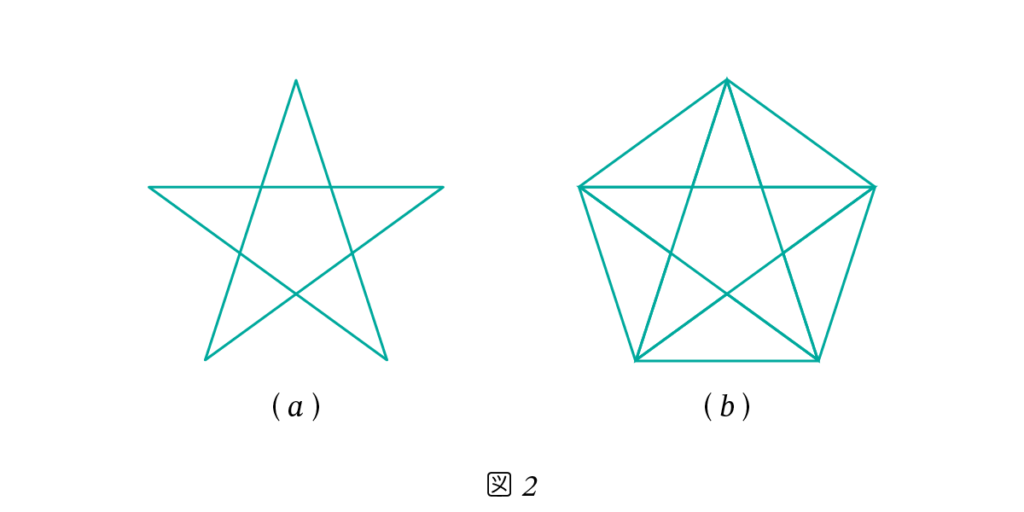
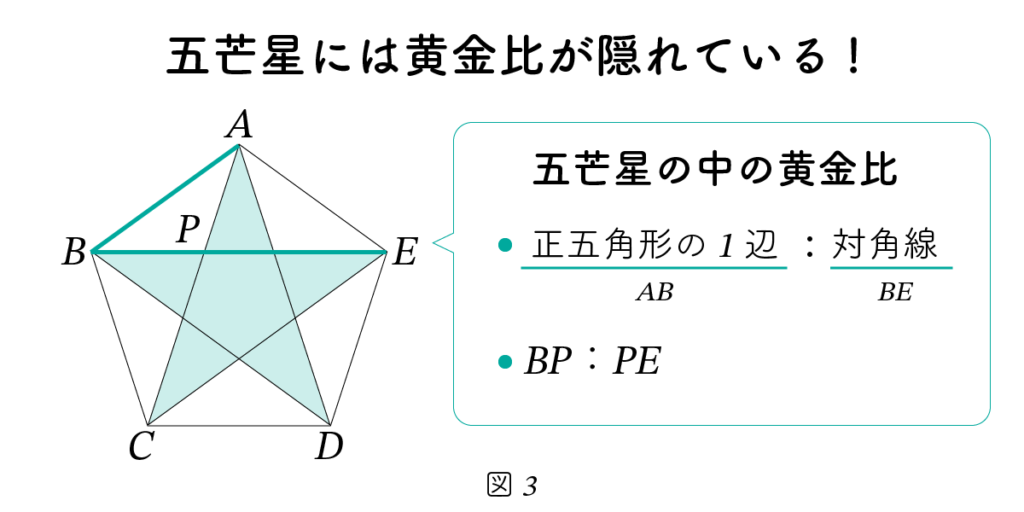
図2-(b)の中にも黄金比がたくさん現れます。代表的な黄金比は 図3のAB : BE、つまり「正五角形の1 辺 : 対角線」です。

黄金比は、芸術家だけでなく自然からも愛され、木の葉の模様や貝殻の渦巻などの自然界の中にも多く発見されます。これらのことは、ピタゴラス※の「自然は数の比によって支配されている」という主張を証明しているように思われました。

黄金長方形

図形のなかには相似な図形をその中に含むといった構造を持つ図形があります。このような構造を 再帰構造 といいます。図4ように、2 辺の比が黄金比 a：b となる長方形を黄金長方形 といいます。

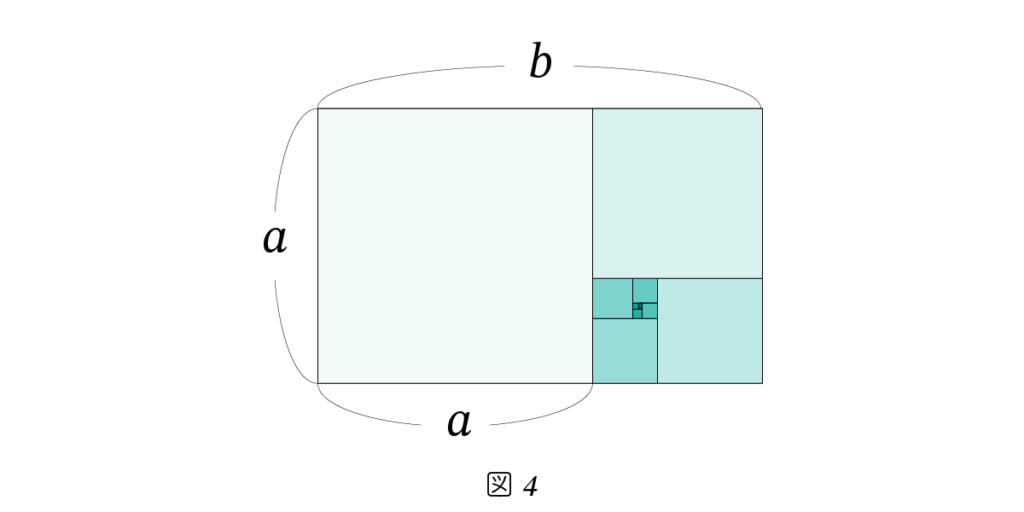
この長方形から、a × a の正方形を切り取ります。すると残りの部分も、黄金比の長方形となります。この残りの長方形に対しても、正方形を切り取るという操作を適用することができ、無限に続く再帰構造が実現できます。 図4はこのようにして、正方形を再帰的に切り取った図形です。巻貝もこの構造を持っています。

ピラミッドにも『 黄金比 』が隠されている？

エジプトの大ピラミッドは世界7不思議の1つといわれ、昔から多くの人が「ピラミッドの謎」について語っています。その謎の一つ「ピラミッドには”黄金比”が隠されている」という話をご存知ですか？

大ピラミッドの底面積に対する側面積の比は黄金比である

というものです。大ピラミッドの底面積を S1、側面積を S2 とします。すると S1 : S2 が黄金比となる、つまり

S1 / S2 = φ = 1.6180339887 …

が成立するというのです。実際に検証してみると、どうやら大ピラミッドの底面積と側面積の比は黄金比になっているようです。なぜピラミッドに黄金比が現われるのでしょうか。これは「偶然の一致」なのでしょうか。

Web連載【ピラミッドに隠された謎】では、この「黄金比の謎」を古代エジプトの歴史や神話、そして古代エジプトの数学能力など、様々な角度から解き明かしていきます。興味のある方はこちらもぜひ読んでみてください▼