4-5.アルキメデスの円周率

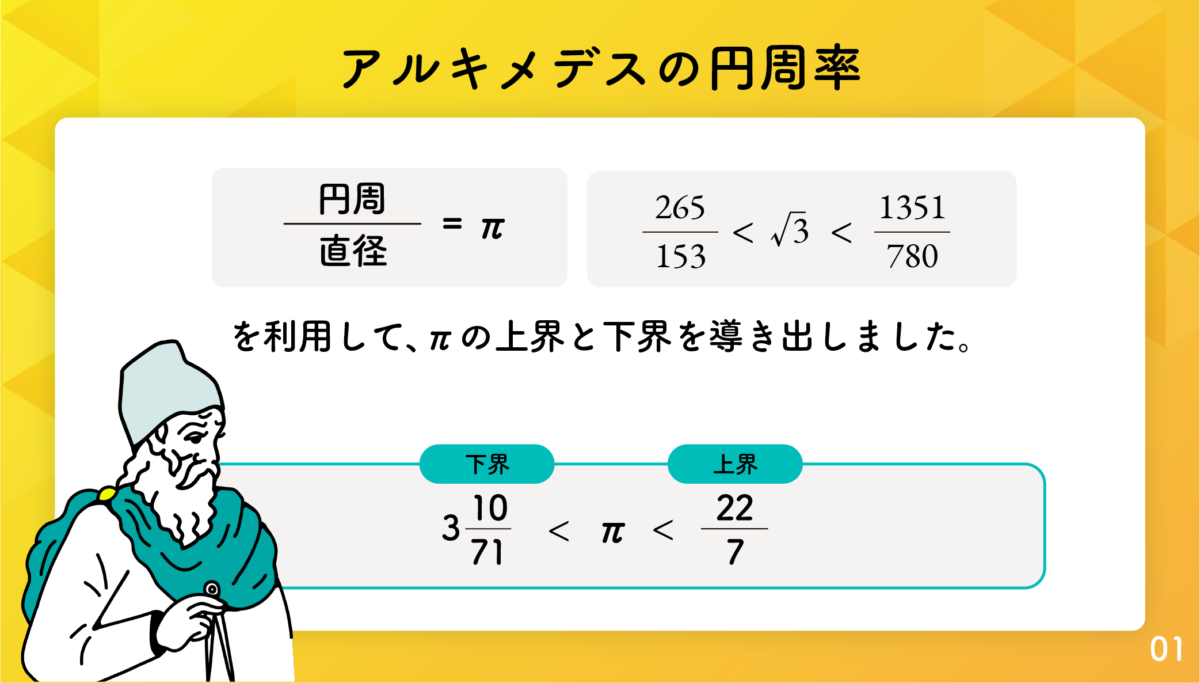
アルキメデスの考えた円周率とは

数学史を通して最も有名な数学者と言えばアルキメデス※です。アルキメデスは、放物線の切片の面積、球の表面積や球の体積など多くの成果を残していますが、そのなかでも円周率 π はだれでもが理解でき、広く一般に知られています。円周率は本連載のテーマの一つでもありますから、アルキメデスがこれをどのように計算しているかを見てみましょう。

アルキメデスの円周率の説明の前準備

1.三角形の補助定理

アルキメデスの円周率の計算の中で次の補助定理を使います。

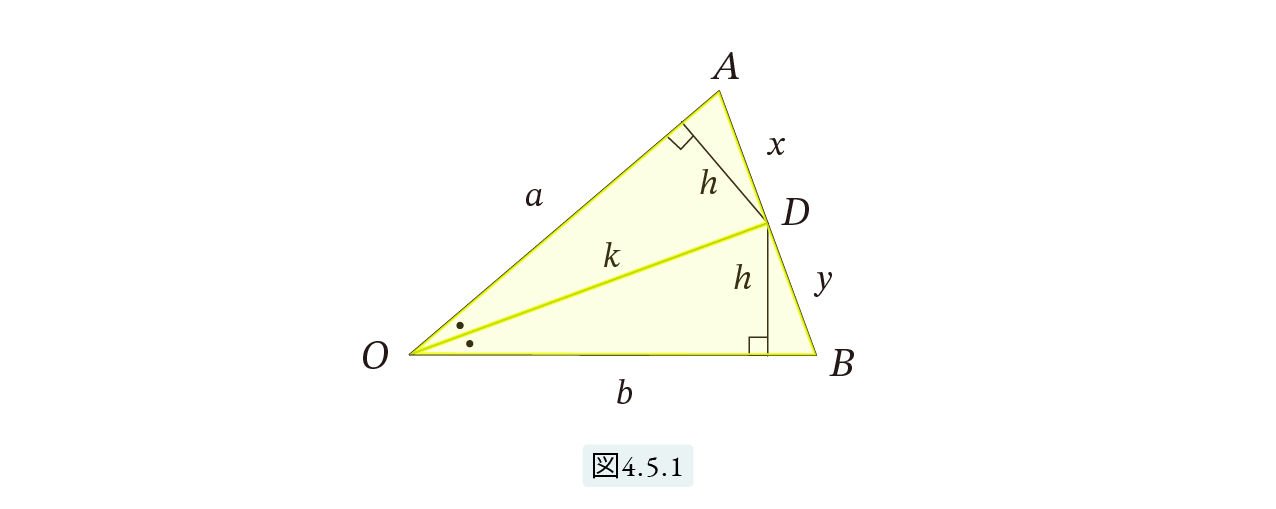
三角形 AOD と BOD の面積を考えます。OD は2等分線ですから、Dから2辺への距離は等しく、これを h と置きます。また、OからAB への距離を k とします。この2つの三角形は、a と b を底辺とみると、高さ h が共通であり、x と y を底辺とみると、高さ k が共通です。『4-2.ピタゴラスの定理』で、高さが等しい2つの三角形の面積は底辺の長さに比例することをみました。したがって次が成立します。

a : b ＝ 三角形AOD : 三角形BOD ＝ x : y

2.開平アルゴリズム

アルキメデスの円周率の計算にでてくるもうひとつのポイントは $\sqrt{3}$です。

x ² = a の正の解を求めること、つまり $\sqrt{a}$を計算することを開平かいへいするといいます。ここで、a は正の有理数とします。バビロニア人は開平アルゴリズムを知っていて、実際に60進小数で何桁もの複雑な計算をしています。アルキメデスもこのバビロニアのアルゴリズムを知っていたようです。アルキメデスは次を用いています。

265 153 < $\sqrt{3}$ < 1351 780 (1)

この式をどのようにして計算したかは後で簡単にふれます。

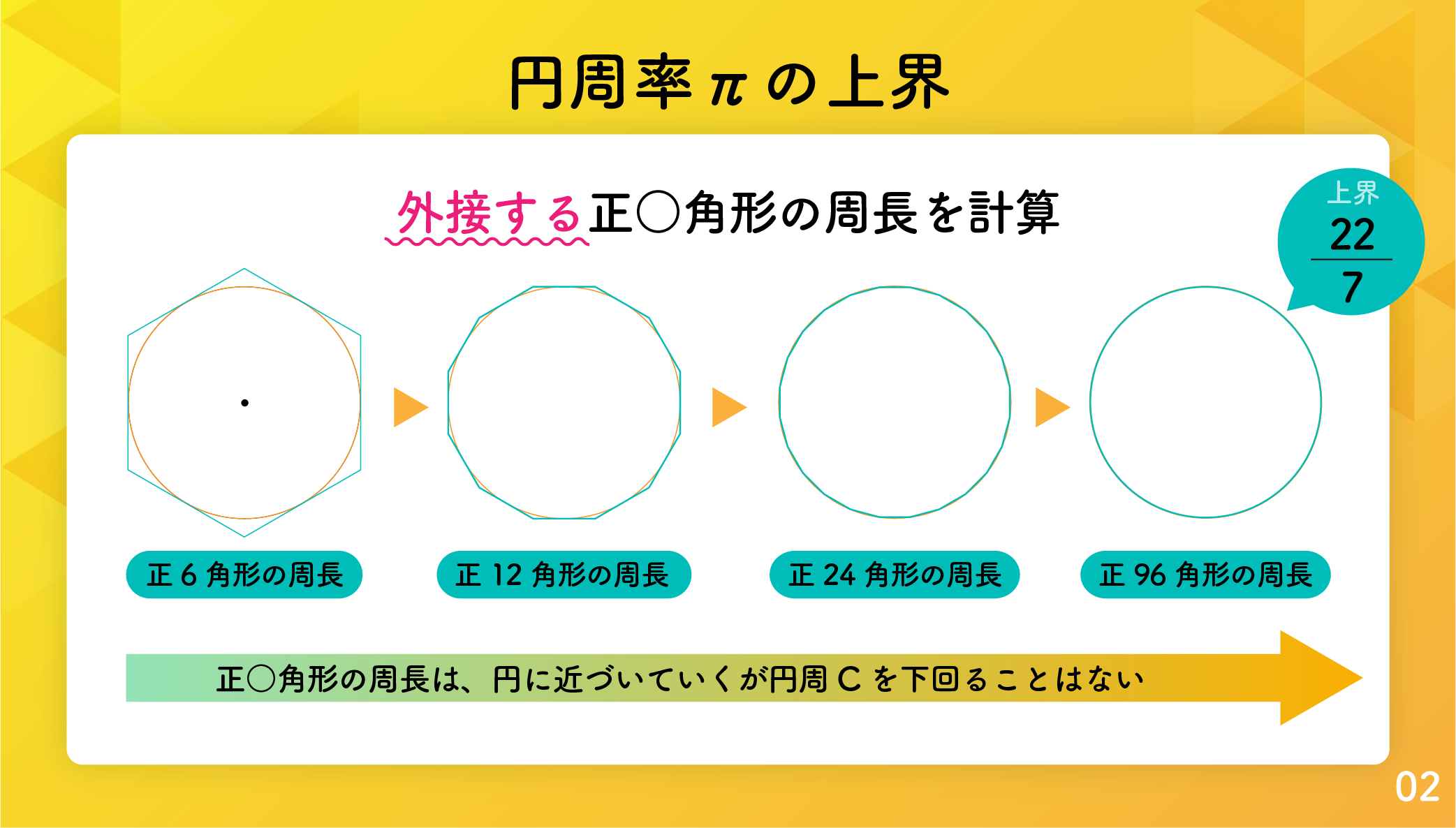
円周率の上界を求める

まずは外接する正６角形の外周を考える

半径1の円 O を考えます。円 O の円周を C とします。現代の皆さんは

C 2 ＝ π ＝ 3.141592 … 　 (2)

であることを知っています。C < α となる数 α を C の上界、β < C なる数 β を C の下界といいます。なるべく C に近い上界と下界を求めることが目的です。

C の上界を示します。アルキメデスは次を示しました。

C 2 < 22 7 = 3.142857 … 　　(3)

注意：議論の本筋から外れますから読み飛ばしてもかまいません。前節で「アルキメデスは長さなどの量に関しては数値自身に意味はなく、つねに比の形で表した」と述べました。(3) を比の形で述べると、本質的に次と同等です。 半径 r の円周 : 一辺が r の正方形の周長　＜ 11 : 7 「円周＝ 2πr, 正方形の周長＝4r」ですから、2πr : 4r ＝ π 2 : 1 となります。

以下では現代数学を使って説明しますが、アルキメデスがやったとおりに言い換えることができます。

アルキメデスは、まず半径1の円 O に外接する正六角形を考えました。図4.5.2 より、正六角形の周長は円周 C より大きいことは明らかです。

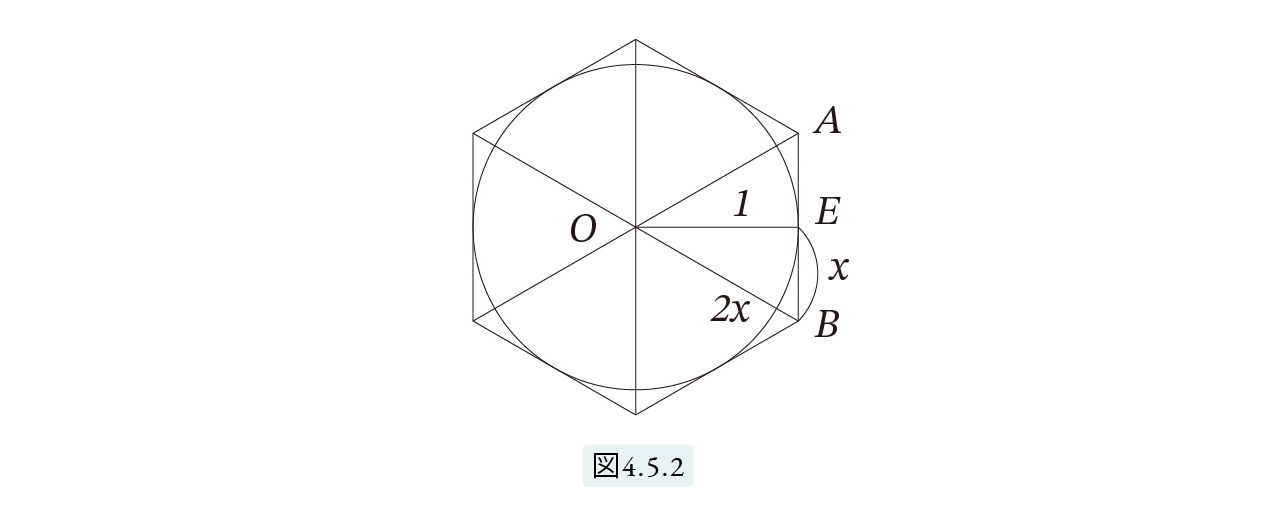
三角形 AOB は正三角形ですから、EB＝x と置くと、OB＝2xです。また半径１の円に外接しているので OE＝1です。したがってピタゴラスの定理より、

4x² ＝ 1² ＋ x², よって x = 1 $\sqrt{3}$ 　　 (4)

となります。正六角形の周長は x の12倍ですから

12x = 12 $\sqrt{3}$ = 12$\sqrt{3}$ $\sqrt{3}$×$\sqrt{3}$ =4$\sqrt{3}$

となります。ここで (1) を使うと(1)を再表示

265 153 < $\sqrt{3}$ < 1351 780 (1)

×

C 2 < 2$\sqrt{3}$ < 2 × 1351 780 = 3.4641 …

となります。しかしこの上界は上の (2) や (3) と比べあまり良い値とは言えません。アルキメデスはこの正6角形から始め、正12角形、正24角形、正48角形と計算してゆき、正96角形まで計算しました。

続いて正12角形、正24角形、正48角形、正96角形の外周を考える

∠AOE の2等分線を OA₁ とします。すると辺 A₁E は正12角形の1辺の半分（つまり 1 2）となります。
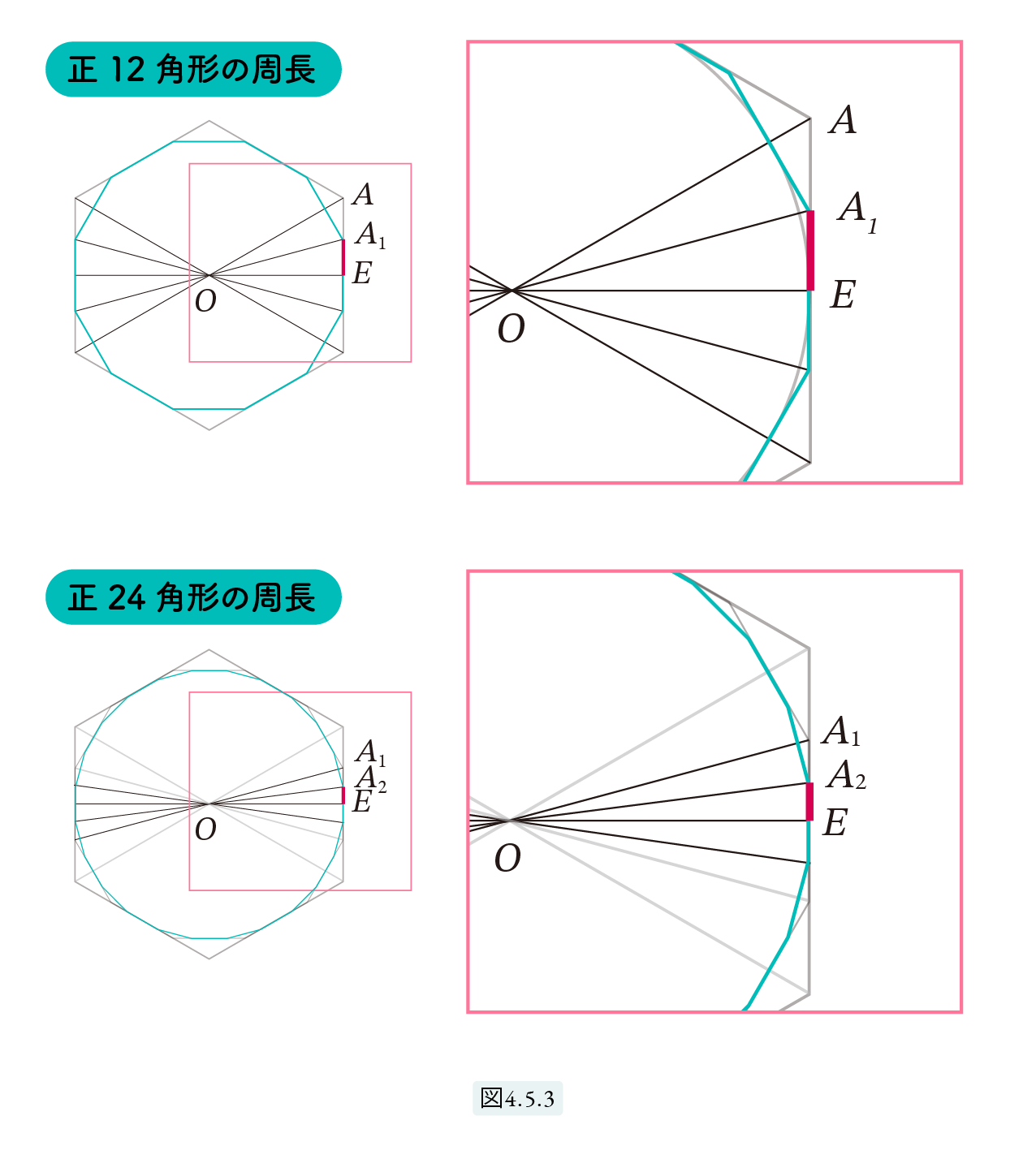∠A₁OE の2等分線を OA₂ とすると辺 A₂E は正24角形の辺の半分となります。∠A₂OE の2等分線を OA₃ 、 ∠A₃OE の2等分線を OA₄ とすると、辺 A₄E が求める正96角形の辺の半分となります。A₀ ＝ A と置き、A_nE ＝ x_n , A_nO ＝ r_n (n＝0,1,2,3,4) と置きます。簡単のため x₀ と r₀ の添え字 0 は省略します。

正12角形の一辺の半分の長さ x₁ の上界を求めます。都合によりx₁ の上界の代わりに 1 x₁ の下界を求めることにします。これと同様の計算が、正12角形から正24角形、正24角形から正48角形、正48角形から正96角形でも行われますので、一般的に述べると次のようになります。

1 x_n と r_n x_n の下界が与えられたとき、1 x_n+1 と r_n+1 x_n+1 の下界を求める

まず (4) より x ＝ x₀ ＝ 1 $\sqrt{3}$ 、r ＝ r₀ ＝ 2x ですから、 1 xと r x の下界は次で与えられます。

1 x = $\sqrt{3}$ > 265 153,　　r x = 2 ≥2 　　　 (5)

1 x₁の下界を求めましょう。図 4.5.4参照。

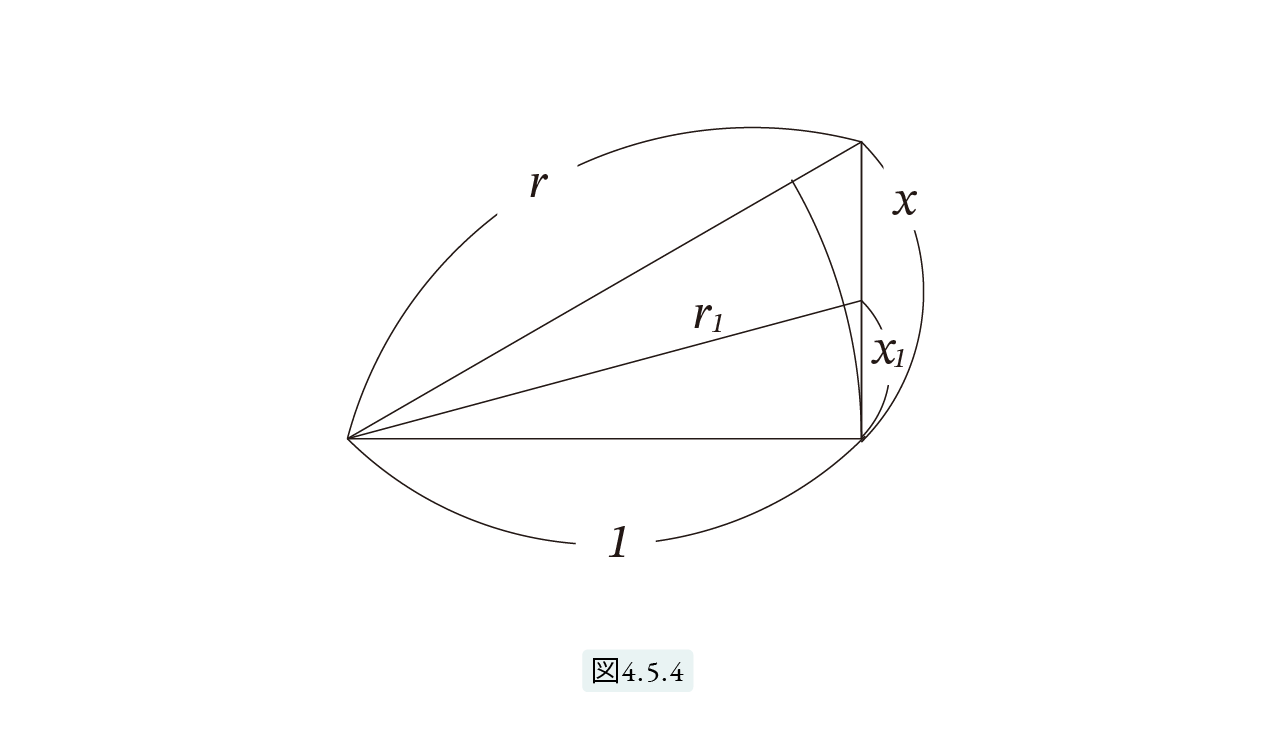
補助定理4.5.1 より

r : 1 ＝ ( x – x₁ ) : x₁

皆さんは分数のほうが慣れていると思うので分数に直します。

r 1 = x – x₁ x₁

両辺に 1 を加えると

r + 1 1 = x x₁

となります（比の理論でもこれと同じ変形ができます）。さらにこれは次のように変形できます。

1 x₁ = r + 1 x = 1 x + r x

ここで、1 x と r x の下界 (5) を使います。(5)を再表示

1 x = $\sqrt{3}$ > 265 153,　　r x = 2 ≥2 　　　 (5)

×

1 x₁ = 1 x + r x > 265 153 + 2 = 571 153

次の計算のために r₁ x₁ の下界も求めます。r₁² はピタゴラスの定理で計算します。

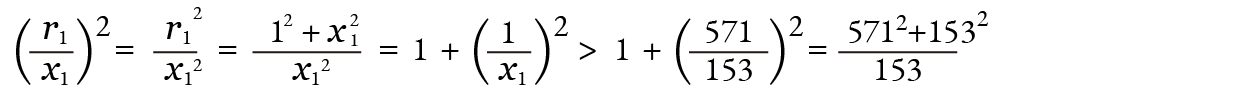
ここで、$\sqrt{{\mathrm{571}}^2+{\mathrm{153}}^2}$ の計算が必要となります。バビロニア人はこのような開平の計算が得意でした。とくに次の平方の公式をよく利用していました。

(a＋b)² ＝ a² ＋ 2ab ＋ b²

この公式を使って、アルキメデスは次のように開平を行っています。まず 153² = 23409 を 2 × 571 = 1142 で割ります。

23409 1142 ＝ 20.498…

小数点以下を切り捨て、20 とします。すると次のように変形できます。

571² ＋ 153²
　＝ 571² ＋ 2×571×20 ＋ 569
　＝ 571² ＋ 2×571×20 ＋ 20² ＋169
　＝ (571＋20)² ＋ 169

これで $\sqrt{{\mathrm{571}}^2+{\mathrm{153}}^2}$ を 571＋20＝591 と近似してもよいのですが、アルキメデスはこれに満足せずさらに続けます。169 2×591 ＝ 169 1182 > 1 7 となります。すると、169 は次のように変形できます。

169 ＝ 2×591×1 7 + 0.142… > 2×591×1 7 + (1 7 )²
ひとつ上の式を続けます。
＝ 591² ＋ 169 > 591² ＋ 2×591×1 7 + (1 7 )² > (591+1 7 )²

1 7 でもよいのですが、エジプト式の計算では1 8のほうが計算しやすいので 1 8 をとります。これより、r₁ x₁ の下界が得られます。

r₁ x₁ > $\sqrt{{\mathrm{571}}^2+{\mathrm{153}}^2}$153 > 1 153 (591+1 8 )

アルキメデスは同様の計算を続けます。つまり、1 x_n と r_n x_n の下界から 1 x_n+1 と r_n+1 x_n+1 の下界を計算します。得られた結果は次のようになります。

1 x₂ > 1 153 (1162 1 8) ,
r₂ x₂ > 1 153 (1172 1 8) ,
1 x₃ > 1 153 (2334 1 4) ,
r₃ x₃ > 1 153 (2339 1 4) ,
1 x₄ > 1 153 (4973 1 2)

最後に得られた r₁ x₄ の逆数を 96倍すると、

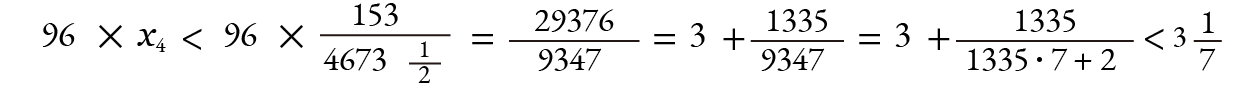
となります。これで (3) が証明できました。つまりアルキメデスが示した円周率の上界を求めることができました。

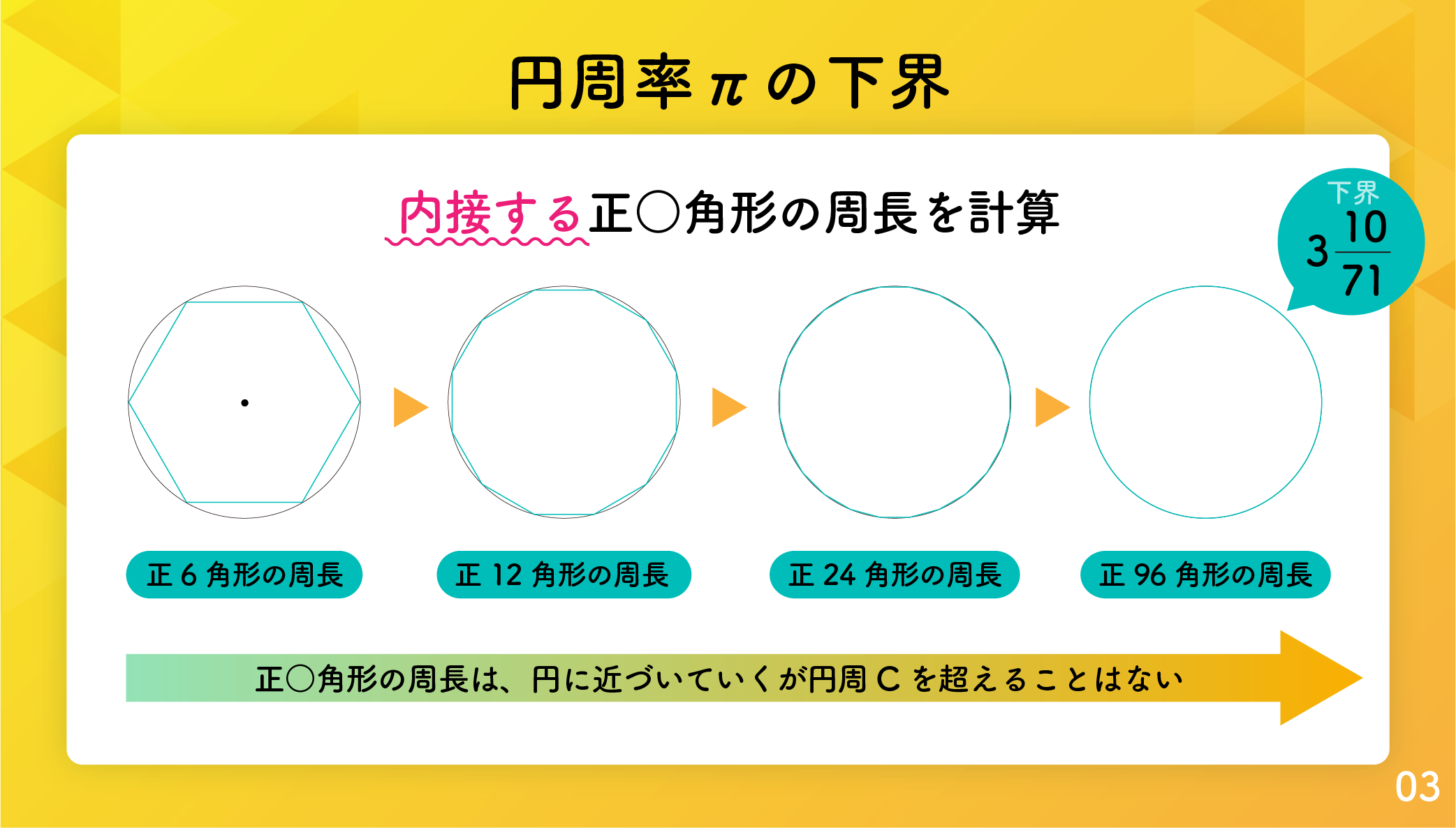
円周率の下界を求める

円周率 π の下界を求めましょう。今度は円 Oに内接する正多角形を考えます。ここでは便宜上円 O の半径を 1 2、つまり直径を 1 としましょう。

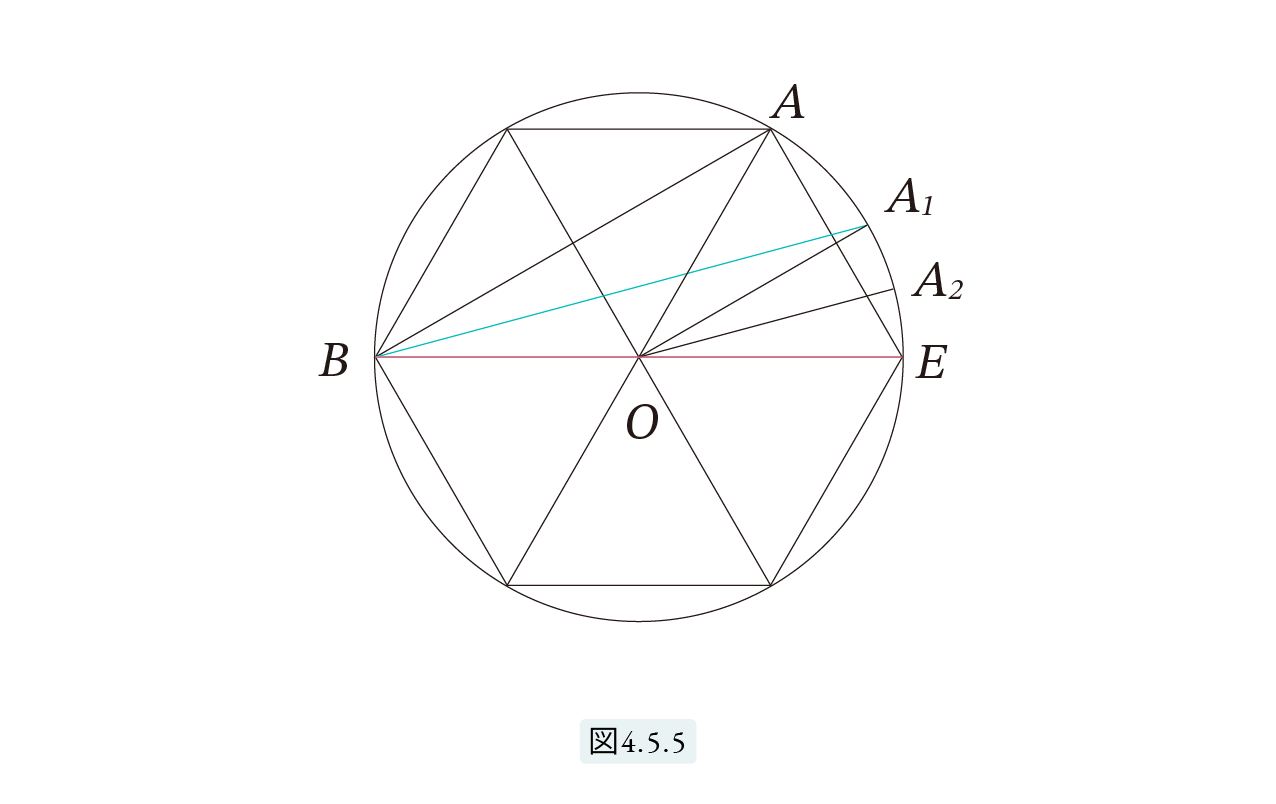
図4.5.5は円に内接する正六角形で、三角形AOEは正三角形です。前と同様、OA₁ を∠AOEの2等分線、OA₂ を∠A₁OEの2等分線、… と2等分していき、正12角形、正24角形、… 、と正96角形まで構成します。しかしこんどは三角形AOE ではなく三角形ABE を考えます。∠AOE は ∠ABEの2倍です。（∠AOE は弦AEの中心角、∠ABEは円周角です。）したがって、BA₁ は∠ABE の2等分線です。同様にして、BA₂ は∠A₁BE の2等分線となります。 A₀ ＝ A と置き、A_nE ＝ x_n, A_nB ＝ r_n (n＝0,1,2,3,4) と置きます。簡単のため x₀ と r_n の添え字 0 は省略します。以下の議論は上の議論とよく似ています。

　

実際はx₄ の下界を求めたいのですが、前と同様に r_n x_n と 1 x_n の上界から、r_n+1 x_n+1 と 1 x_n+1 の上界を計算します。 r x と 1 x の上界は次で与えられます。

r x = AB AE= $\sqrt{3}$1 < 1351 780,　　1 x = BE AE = 2

図4.5.6 を見てください。

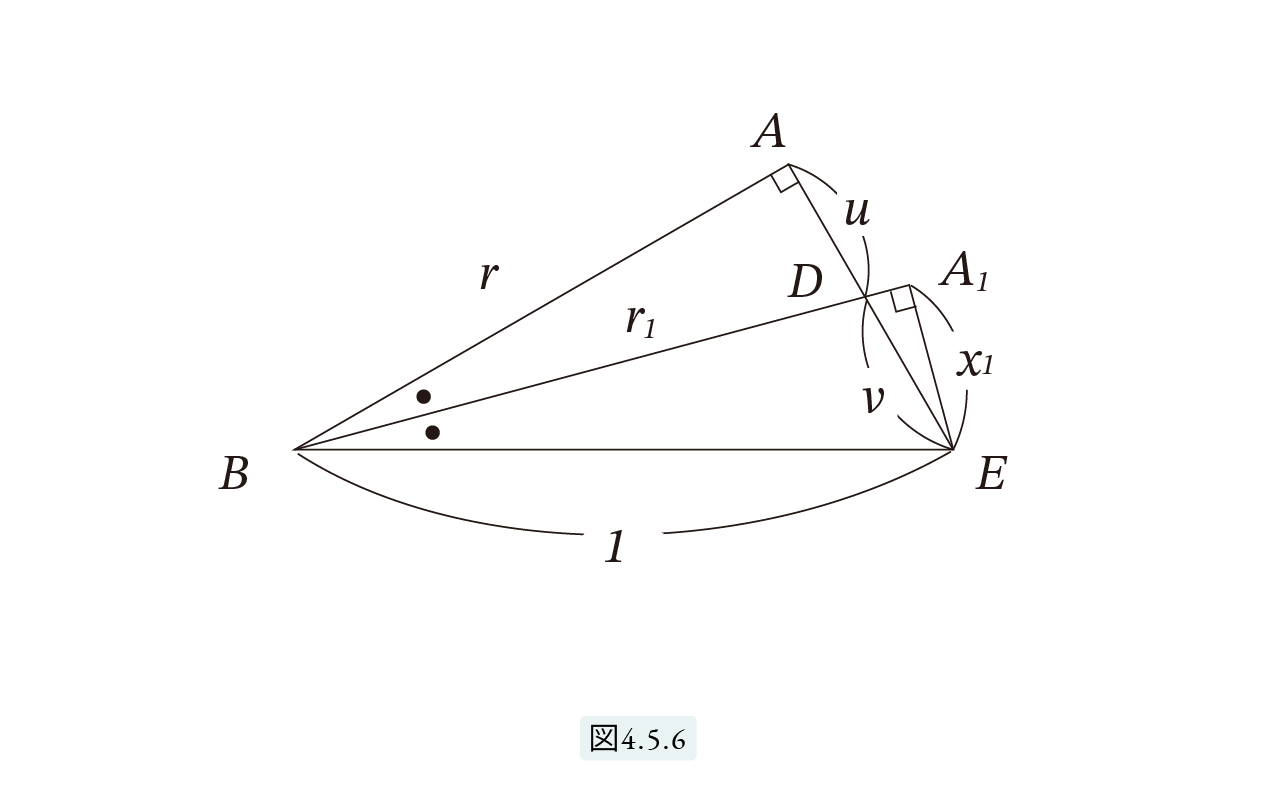
三角形 ABD と A₁BE は対応する2つの角が等しいので相似です。一組は∠B の半分、一組は直角です。したがって、

r : u ＝ r₁ : x₁

が成り立ちます。分数で表すと、

r₁ x₁ = r u 　　　 (6)

となります。また、補助定理4.5.1 より、

r : 1 ＝ u : v

「内項の積＝外項の積」を適用すると、

u ＝ rv 　　　　(7)

が成り立ちます。(6) と (7) より

r₁ x₁ = r u = 1 v 　　 (8)

が成り立ちます。u ＝ x – v を (7) に代入して整理すると、x＝(r＋1)v となりますから、1 v ＝ r+1 x と (8) から次が得られます。

r₁ x₁ = r+1 x = r x + 1 x

ここで、r x と1 x の上界を用いると、

r₁ x₁ < 1351 780 + 2 = 2911 780

が得られます。また、三角形 A₁BE は直角三角形だから、

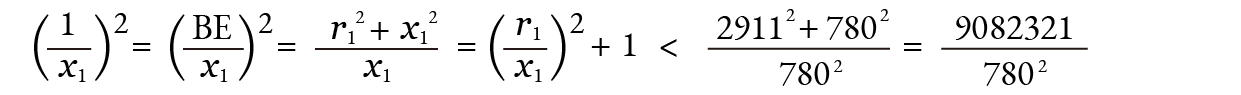
が得られ、これより

1 x₁ < $\sqrt{\mathrm{9082321}}$ 780 < 1 780 (3013 3 4)

が得られます。同様の計算を繰り返すことによって、アルキメデスは次の結果を得ます。

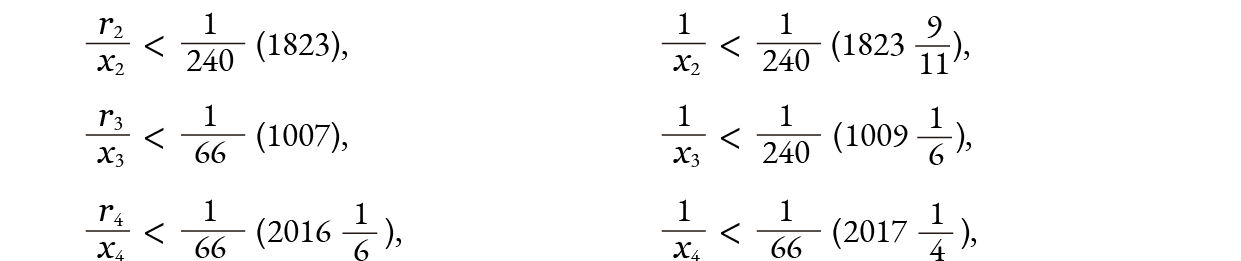
最後に得られた 1 x₄ の逆数をとって、96倍すると、

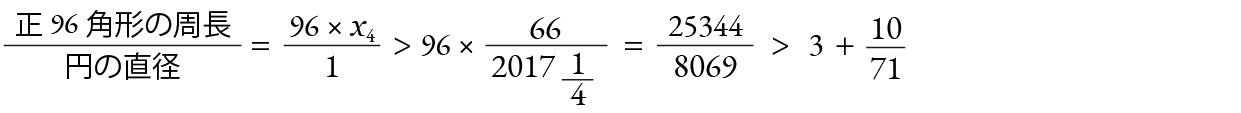
が得られます。これでアルキメデスの示した円周率の下界が求められました。

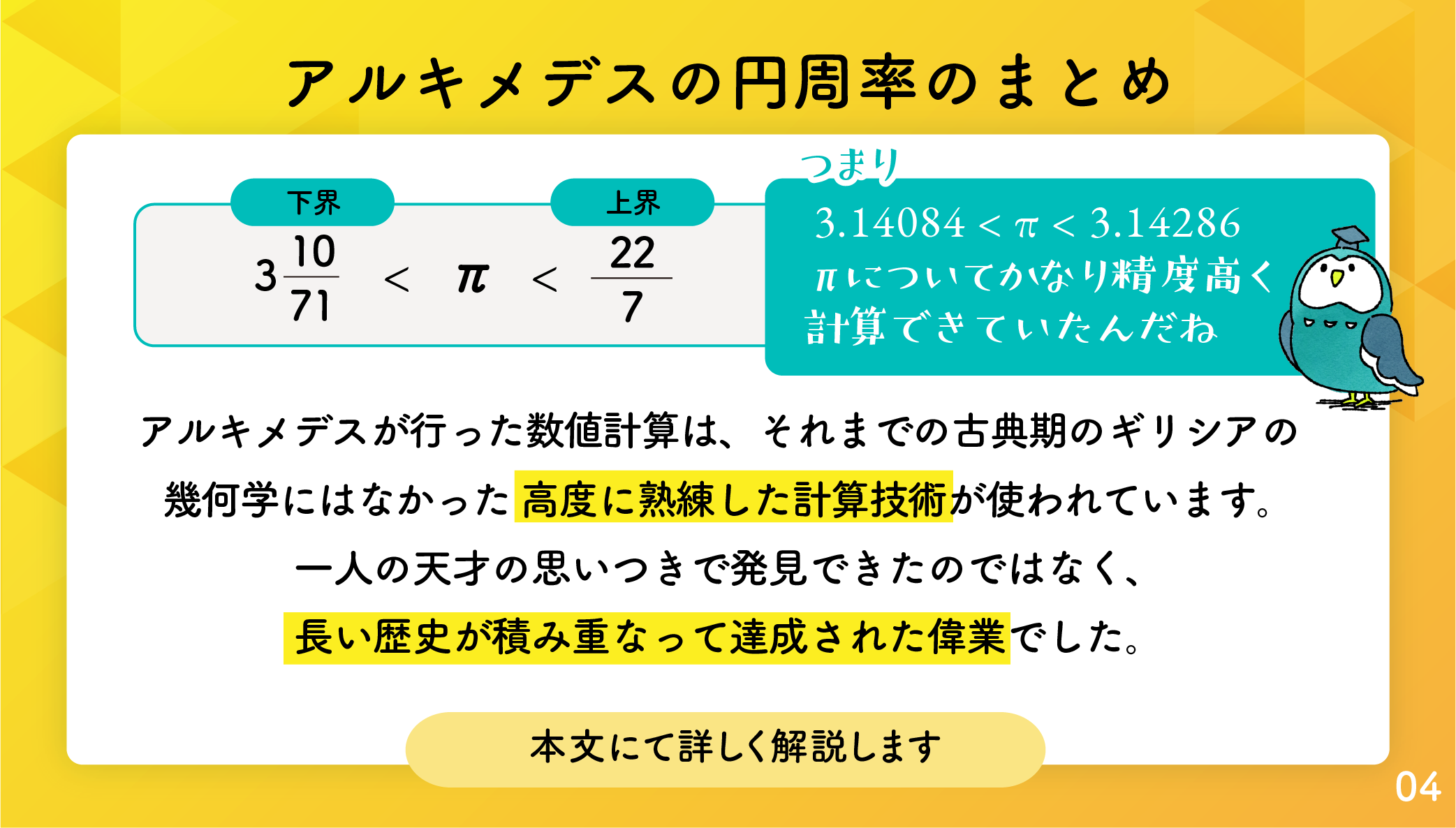
以上で得られた結果をまとめると、

3 10 71 < 正96角形の周長/円の直径 < 3 1 7

となります。

アルキメデス と√3

この計算のはじめで、 アルキメデスは $\sqrt{3}$ の近似値として

265 153 < $\sqrt{3}$ < 1351 780

を用いていることを述べました。おそらくこれは次のようにして計算したのではないかと考えられます。

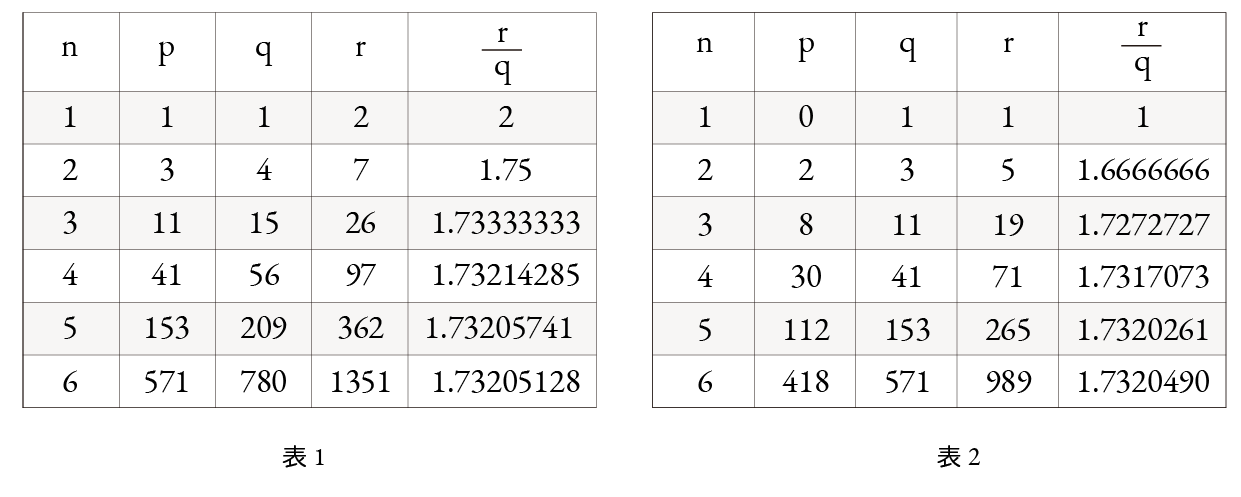
まず表1の作り方を述べましょう。現代式に漸化式で表すと次のようになります。

p₀ = 1,　　q₀ = 1
r_n = p_n + q_n ,　　p_{n + 1} = q_n+ r_n ,　　q_{n + 1} = p_{n + 1} + q_n,　　n = 0,1,2,…

表2は初期値が違うだけで、初期値は次で定義されます。

p₀ =0,　　　q₀ =1

漸化式で書くとむつかしそうですが、実際に実行してみると意外と簡単です。バビロニアの記数法はギリシアよりは格段に進んでいましたが、計算を筆算でするのは無理でした。板に石を置いて計算するアバクスと呼ばれる計算盤を使っていたと思われます。アルキメデスもアバクスを使っていたと思われます。上の表1 と表2 は、アバクスでの計算の履歴を記録したものです。現在の私たちは“表”が使えますから、表で説明します。 表には3つの欄、 p 欄、q 欄、r 欄があります。第1行目の p 欄とq 欄には1 を書き、r 欄にはその和を書きます。次の行の p 欄には1つ上の行の q 欄とr 欄の和を書きます。 q 欄は左の p 欄と1つ上の行の q 欄の和です。r 欄は同じ行の p 欄と q 欄の和です。足し算しか使っていないので、慣れれば簡単に計算できます。r q 欄は実際に表計算に使う欄ではなく、r q の値を 10進小数で表したものです。表1 では r q の値が上から $\sqrt{3}$ に近づいていき、表2 では下から近づいていきます。$\sqrt{3}$ の上界の 1351 780 は表1の6行目に現れています。また下界の 265 153 は表2 の5行目に現れています。 この表で、なぜ $\sqrt{3}$ の計算ができるかの説明は省略します。

まとめ

この節で行った $\sqrt{3}$ の計算や、アルキメデスが上で行った数値計算は、それまでの古典期のギリシアの幾何学にはなかった高度に熟練した計算技術が使われていることに注意が必要です。このように、大きな数値の平方根の計算法は、それまでの古典期のギリシアの幾何学にはなかった一人の天才の思いつきで発見できたのではなく、そこにはアバクスを使った計算技術などの長い歴史が積み重なって達成された偉業なのです。