3-2.比と傾き：クフ王の大ピラミッドの勾配(セケド)

比の概念と古代の数学

本節では古代エジプトで、比や傾き(勾配セケド)がどの様に扱われていたか。について詳しくみていきます。

消費税10パーセントとか、バーゲン50%オフとか、明日の雨の確率30% など、私たちの身の回りには比があふれています。比とか比率とか比例という概念は、数学にとって最も基本的なものです。円周率や黄金率も比の一種ですが、エジプト人はこの概念をどの程度理解していたのでしょうか。

ギリシアの幾何学の書『原論』には比の明確な定義があり、現在数学から見ても遜色のない「比の理論」が展開されています。『原論』はユークリッド※による立派な著作物であり、人に読ませるように書かれた数学の最初の著作物といってよいでしょう。一方、出土したエジプトの数学文書は、書記のための教科書、いわば現在の受験の問題集のようなものであり、単に問題の羅列です。ですから、これらの史料からエジプトとギリシアの数学を単純に比較することはできません。

古代エジプト人が解いていた比の問題

エジプトの出土したパピルスから判断すると、比に関する次のような問題はエジプト人にとって朝飯前の簡単な問題だったようです。

4人に3個の割合でパンを配ります。10人に配るには何個のパンが必要ですか。

4kg の小麦で3ℓ のビールができます。10kg では何 ℓ のビールができるでしょうか。

4メートル進むと3メートル登る坂があります。10メートル進むと何メートル登りますか。

これらの問題はみな同じ論理構造をしています。私たちは新しい概念を習得するのにとても苦労します。同じような概念を一つにまとめると覚えるのが楽になります。上の問題は比という概念でまとめることができます。現在の私たちは方程式が使えます。上の3つの問題は未知数 x を使うと次のように表現できます。

4人に3個の割合は、10人に x個の割合に等しい。

4kg の小麦の3ℓ のビールの濃度は、10kg の小麦のx ℓ のビールの濃度に等しい。

4メートル 進むと3メートル 登る傾斜は10メートル進むとxメートル登る傾斜に等しい。

上の3つの問題は、図3.2.1のようなグラフで表されます。問3 ではグラフは実際の坂道を表しています。このグラフでは、右に1進むと上へ 3 4 進みます。3 4 をこのグラフの傾きといいます。

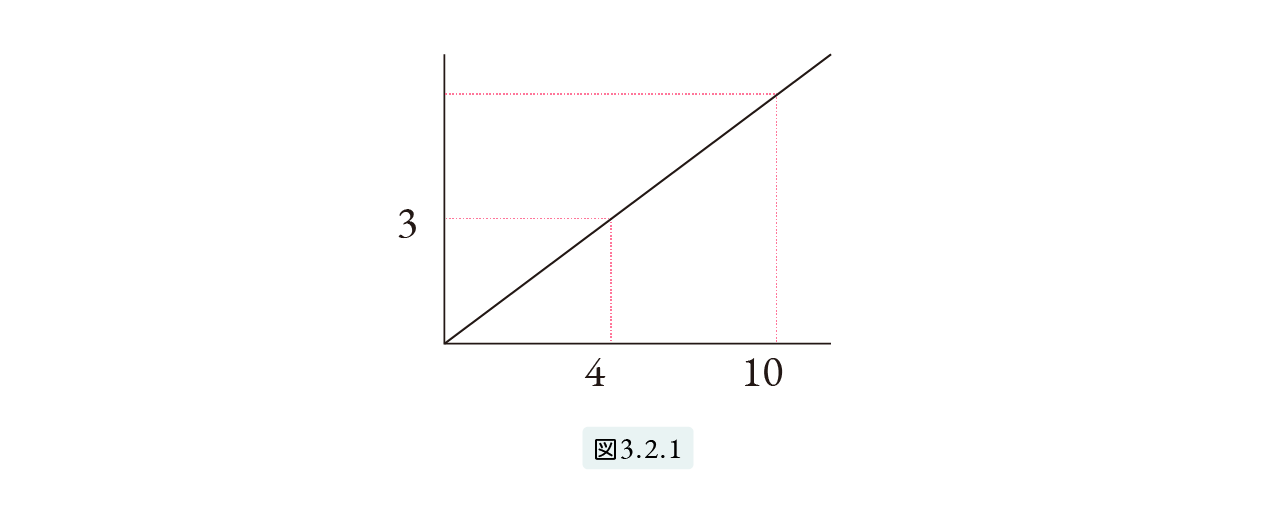
皆さんは急な坂とゆるやかな坂をどのように区別しますか。角度も一つの方法で、数学ではいま述べた傾きという概念を用います。　図3.2.2 のような直角三角形 CABを考えます。AC と AB のなす角をθ、AB ＝ a、CB ＝ h とします。

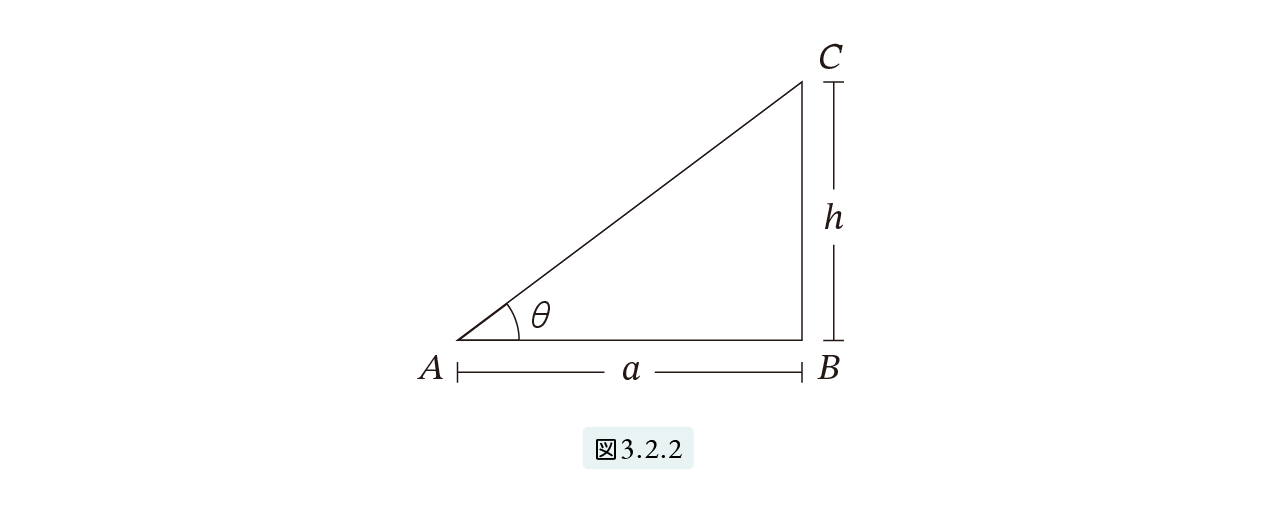
直角三角形 ABC を坂だと考えてください。私たちはこの坂のゆるやかさ加減、つまり傾きの度合いを測るのに分数 h a を用います。これは、水平に a だけ進むと垂直方向に h 上がることを表します。言い換えると

傾き ＝ 1単位進むごとに上昇する長さ

となります。交通標識で傾き 5% の坂といえばこの意味で、100メートル進むと100メートルの 5%、つまり 5メートル上がる坂のことです。

勾配(セケド)と傾きの関係

もう一度図3.2.2 を見てください。直角三角形ABC で、角度θシータがわかれば傾き h a がわかります。これは「三角関数 tan の表」があればそれをみればわかりますが、関数電卓があれば簡単に計算できますからやってみてください。tan は「タンジェント」と読みます。たとえばθが 45度の場合 tan(45) とキーを打つと、1 という答えが表示されます。逆に、傾きから角度を求める場合は、関数 tan^-1 を使います。この関数は「アーク・タンジェント」といいます。tan が何者であるか知る必要はありません。「角度θが与えられたら、その傾きが出力される」とわかれば十分です。もちろん古代人は tan など知りません。これは皆さんの計算のためのものです。

エジプト人は、坂のゆるやかさ加減を測るのに「傾きの逆数」、つまり a h を使っていました。現代の私たちにとって混乱するのは、エジプト人は a と h とで異なる単位を使っていたことです。つまり、底辺は掌尺パームで、高さは腕尺キュビットで測っていたのです。正確にいうと坂の緩やかさ加減を次で定義される「勾配セケド x 掌尺パーム」という表現で表しました。

勾配セケド x 掌尺パーム ＝ x 掌尺パーム水平に移動すると 1腕尺キュビット上昇する

私たちにとって底辺と高さの単位が異なると混乱しますから、以下では高さと底辺を共に腕尺キュビットで測ることにします。図3.2.2 において、a と h の単位を共に腕尺キュビットとすると、a 腕尺キュビット ＝ 7a 掌尺パーム ですから、この坂の勾配セケドは

勾配セケド ＝ 7a h = 7×底辺 高さ(1)

となります。(1) を「勾配セケド ～　掌尺パーム」の定義と見なしてください。以下では「掌尺パーム」を省略して、単に「勾配セケド～」と書きます。現代の皆さんにとっては次の公式を覚えるのが手っ取り早いでしょう。傾きと勾配セケドは互いに「逆数」の関係ですが変換するときには「7倍すること」をお忘れなく。

傾き ＝ 7 勾配セケド,　　勾配セケド ＝ 7 傾き (2)

パピルスにでてくる勾配セケドの問題

次の問題は出土した実際のパピルスにあった問題です。これらを練習問題とし、古代エジプト人がどれくらいの計算能力を持っていたのかみてみましょう。

勾配セケドは本来高さが与えられたとき底辺を求めるためのものです。つまり、勾配セケドに高さを掛けると底辺が得られます。しかし、問題3.2.2では逆に底辺から高さを求めています。この問題を解くには「分数の割り算」が必要です。現在の分数でも割り算は理解するのが難しいのですが、エジプト人は、エジプト分数で割り算を実行しています。分数という概念を十分理解していないとできません。

エジプト分数の割算については以下の記事でも書いています。ぜひご覧ください。

問題3.2.1～　問題3.2.3 はリンド・パピルス※という数学文書に実際にある問題です。このことから、エジプト人はピラミッドの建設に勾配セケドという概念を使って設計していたことが分かります。エジプト人にとって、ピラミッドの底辺の長さと勾配セケドから高さを計算することは簡単な練習問題だったのです。

クフ王の大ピラミッドの勾配セケド

『1-1.ピラミッドの謎とは』で述べたクフ王の大ピラミッドの勾配セケドを計算しましょう。勾配セケドは当時の長さの単位の腕尺と掌尺パームを使って定義されていますが、比ですから現在の単位メートルと、あるいは傾きを使っても計算できます。傾きを使って計算してみましょう。

大ピラミッドの表面の石や、頂上部の石は欠損していますが、傾きは残っている石からだいたい予想ができるようです。たいていの本では 51度50分となっていまが、51度50分40秒 としている本もあります。まず、これらの分秒表示を 10進数に変換します。

51度50分 = 51+50 60度 = 51.833333度

51度50分 40秒 = 51+50 60度 + 40 3600 = 51.844444度

角度θの傾きは tanθ で計算できます。また勾配セケドは傾きより、上の (2)「勾配セケド ＝ 7 傾き」で計算できます。

tan 51.833333 = 1.272295703,　　　勾配セケド 5.50186 掌尺パーム

tan 51.844444 = 1.272803663,　　　勾配セケド 5.49967 掌尺パーム

どちらの数値をとってもクフ王の大ピラミッドは勾配セケド5;1 2掌尺パームとみてよいと思います。この計算で使った角度とtan は現在の数学で用いている道具ですが、当時の長さの単位を用いなくても、勾配セケドを求めることができるのです。

エジプト人はピラミッドの設計や造設に勾配セケドという概念を用いていたこと、大ピラミッドの勾配セケドは 5;1 2 という簡単なエジプト分数で表されることが確認できました。

ペスの問題とは

エジプト人は斜面の傾きを勾配セケドという比で表していたことが分かりました。しかし、勾配セケドだけでエジプト人が“比”の概念を習得していたとは言えません。次にペスの問題と呼ばれている問題について考えてみましょう。この記事のはじめで、小麦の量と小麦からできるビールの量の比の問題について考えました。現代の私たちは普通、1リットルのビールを作るのに何キログラムの小麦が必要かを考えます。人口密度とか比重なども同じ考えです。ところがエジプトでは逆に「1キログラムの小麦で何リットルのビールができるか」を考えます。つまり、ビールから見ると濃さではなくて薄さとなります。また単位もリットルではなくてエジプトの単位となります。

現代数学は、意味ではなく形式で理解します。したがって、「高さ 底辺」でも「底辺 高さ」でも本質的には同じです。同様に、単位が腕尺でもメートルでも問題の難しさは変わらないはずです。しかし、多くの人は単位が変わったり、濃さが薄さに変わったりすると、とたんに難しく感じるようです。学校では、問題を解くとき「意味を理解するように」と、教わると思います。しかしいったん一つの場合をしっかり理解したなら、後は形式的に、つまり公式適用して解いた方が楽なことが多いのです。言い換えると、“意味を理解する”ことも大切ですが、“形式”（つまり“公式”）を覚えることも、多くのことがらを手短に理解するのにとても有効的なのです。以下の問題でこのことを試してみてください。

“ペス”は“料理する（ペシ）”という言葉に由来し、パピルスに書かれた“ペス”という単語から、これらの問題をペスの問題と呼ぶようになったそうです。ペスとはパンとかビールなどで使われる小麦の量の薄さを表すので、これを薄度ペスと呼ぶことにします。つまり、使われている小麦の濃さではなく薄さを表す値です。

薄度ペス＝製品の個数 使われた小麦の量

たとえば 1枡ヘカトの小麦で5個のパンができたときは、「このパンは薄度ペス5個」といいます。薄度ペスが分かっていれば、与えられた小麦でどれだけのパンが作れるかが分かります。現代では、たとえば秒速は m/sec ＝ メートル/秒 のような単位名が用いられます。薄度ペスの単位名をこのように現代式に表すと、パンの場合は「個/枡ヘカト」、ビールの場合は「杯はい/枡ヘカト」となるのですが、 以下の記述ではエジプト人の表記に合わせて、「/枡ヘカト」の部分は省略することにします。これを公式として次のようにまとめます。

薄度ペス＝ 個 枡ヘカト　または　　薄度ペス＝ 杯 枡ヘカト (3)

問題3.2.4

この計算では 80×2 7 をエジプト分数に直していますが、この直し方の説明はここでは省略します。エジプト人は分数の割り算を使った計算をしていたことに注意してください。

問題3.2.5

公式と方程式を使った現代式の方法は、いつも同じような方法で“意味”を考えずに解くことができることです。

問題3.2.6

問題3.2.7

問題3.2.8

次は方程式を使わないとちょっと難しい問題です。パンの薄度ペスの 1 10がビールの薄度ペスといっていますが、これはパン1個を作るのに必要な小麦の量の10倍の小麦が必要だ、という意味です。 しかし、方程式で解く場合はこのような意味を考えなくても、形式的にパンの薄度ペスの1 10 をビールの薄度ペスとすれば計算できます。

問題3.2.9

まとめ

以上の考察より、古代エジプト人はピラミドの斜面の角度をあらわす寸デジット勾配セケドだけでなく、パンやビールの薄度ペスなど、比の一般的な概念を身につけていたことが分かります。さらにこれらの概念を用いた面倒な計算問題を、エジプト分数を用いて正確に計算していました、これは後のギリシア数学にはない特徴です。