1-1アルキメデスと無限

アルキメデスは、世界中の誰でも知っているほどの有名人で、彼の行った研究は現代数学発展の大きな礎(いしずえ)となりました。特に、基本的な図形や立体の、面積とか体積を求める方法（これを求積といいます）は、のちのニュートンやライプニッツによる積分法に発展します。2千年以上も昔に、現在の高校数学で習うような、放物線とか楕円を扱っていたのです。驚くべきことだとは思いませんか。ほかの科学、たとえば化学、医学、生物学などでは考えられません。2千年も昔とほとんど同じ内容が現在でも通用するのは数学ぐらいです。

古代の数学を学ぶということ

数学は言語である

これは数学のもつ大きな特徴の一つなのですが、このことがかえって数学史や数学教育の大きな障害となっているのです。科学史（数学史）の専門家は、よく「古代の科学（数学）を述べるのに、現代の概念や技術を用いてはならない。当時の概念や技術で述べなければならない」と注意します。しかしこれはとても難しいことなのです。アルキメデスの原著の翻訳では、専門家が苦労して原文の意味を変えないように正確に翻訳しています。この場合、分かりやすい簡単な表現に書き換えると、原文の意味が変わってしまうことがあります。

「数学は言語である」とよくいわれますが、数学も言語としてずいぶん進歩しているのです。現代数学の術語や概念を使うと、わかりやすい表現になりますが、古代のものと違ったものとなることがあるのです。

数学とは何か

本連載の目的は、古代の数学自体にあるのではなく、古代の数学を通じて「数学とは何か」を知ってもらうことです。数学もほかの科学と同様に進歩しているのです。アルキメデスの理論は、12世紀に入って西ヨーロッパに入ってきましたが、当時はまだ数学や自然科学が未発達でなんとか受け入れることができるようになるまでには、さらに300年もの年月を必要としました。オリエントで発達した数学に追いつくのに300年も要したのです。アルキメデスが活躍したシチリアは、今ではイタリア領ですが、イタリア本土には伝わっていなかったようです。

というわけで、本連載では現代数学の用語や概念を使うことにします。ただし、当時ではまだ得られていなかった概念には細心の注意を払うことにします。

古代における数は自然数だけだった

「数」と「量」

最も注意すべきことは“数”に関してで、古代では“数”と認識していたのは個数、つまり自然数だけでした。長さ、面積、体積、角度、重さ、… などは“量”として扱われ、量には数値が割り当てられることはありませんでした。

2つの量は足したり引いたりすることがあります。このことが許されるのは2つの量が同じ種類の量のときに限ります。たとえば、「長さと面積」など違った種類の量は足したり引いたりできません。同様に、2つの量は、どちらが大きいか、あるいは等しいかが比較されることがあります。この場合も、比較できるのは2つの量が同じ種類の量のときに限ります。

合同とは何か

“長さ”や“面積”や“体積”といった言葉は、それぞれ線分とか平面図形とか立体の持つ属性で、古代ではまだこのような概念がなく、単に大きさと呼んでいました。図1.1.1 のような三角形を、「三角形ABC」と呼び、△ABC と表すことにします。

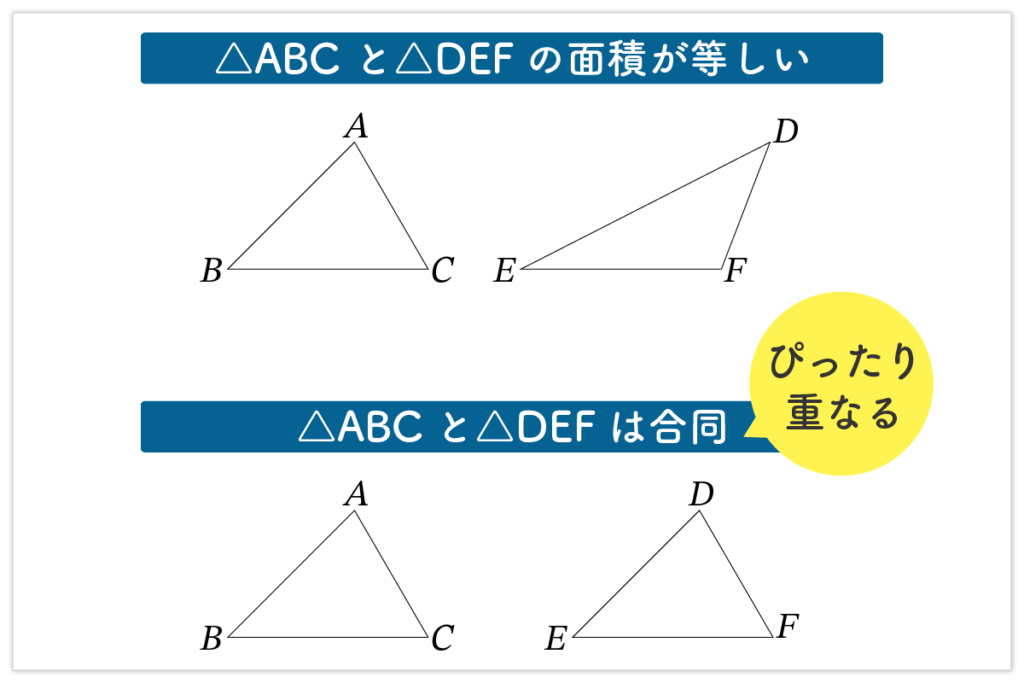
△ABC と △DEF の面積が等しいときとき、△ABC と △DEF は等しいといい、

△ABC ＝ △DEF

と書きます。△ABC と △DEF がぴったり重なるときは、△ABC と △DEF は合同であるといいます。“合同”よりも“等しい”ほうが広い概念であることに注意してください。円や長方形など、その他の平面図形に対しても同様です。この方式はとても便利なので、現在でもよく用いられます。

量に関して最も重要なことがらは量同士の掛け算が許されていないことです。

古代ギリシアの論証数学

ギリシアで発明された論証数学とは、与えられた公理と定義だけを前提とし、決められた推論規則だけを用いて論証する体系のことです。しかし、初心者がこれを体得するには時間をかけた練習が必要となります。手っ取り早く「ユークリッドの幾何」を理解するために「ユークリッド幾何ではコンパスと定規以外は使っていけない」と述べられることがあります。「『原論』にはそんなことはどこにも書かれていない」と、専門家の注意を受けることがありますが、初心者が「ユークリッド幾何」を理解するにはよい方法だと思います。同様に、アルキメデスの理論を理解するためには「量×量は許されない」と考えるのがよいと思います。

数学用語 の復習【 基礎編 】

直線と線分

ここで、本連載で用いる用語の説明をしておきます。左右に無限にのびたまっすぐな線を直線といい、長さが有限のまっすぐな線を線分といいます。2つの線分は重ねることによりどちらが長いか分かります。ぴったりと重なるとき等しいといいます。2つの線分 a と b はつなぎ合わせることができます。つなぎ合わせたものを a＋b で表します。a を線分、n を自然数とします。a をn個つなぎ合わせたものを na と書きます。一般に、量同士の掛け算は禁止されますが、量の自然数倍は許されます。

長方形

線分のことをときどき辺と呼びます。a と b を辺とします。2つの辺 a と b で作られる長方形を □(a,b) で表すことにします。上で述べたように、□(a,b) は長方形を表わす場合と、その長方形の面積を表わす場合の両方があります。長さ a と b の積 a×b は許されません。その代わりに □(a,b) が用いられます。皆さんは、□(a,b) を a×b と解釈すると理解しやすいと思います。ある著作では「ギリシア人は量 a と b の掛け算を □(a, b) で定義した」といった記述を見かけましたが、これは間違いです。そもそも古代ギリシアでは量同士の積という概念はなかったのですから。

エジプトのアレクサンドリアは、ヘレニズム時代には地中海貿易の拠点として栄えます。またアルキメデスが活躍したシチリア島の都市シラクサも古くからギリシアなどの植民地として活発に活動しています。商業活動には数値が必須です。布などの大きさは面積、ワインなどの容量は体積です。なぜ数学において、ギリシア人は長さ、面積、体積を数値と結びつけなかったのでしょうか。

古代ギリシアの「単位」とは

現在の私たちは、長さの単位としてメートルを使用しています。世界中どこに行っても1メートルは同じ長さです。さらに、細菌やウィルスなどの小さいものから、太陽の直径とか宇宙の直径のような大きなものまでメートルで測ることができます。しかし、このように1メートルを、普遍的で絶対的な単位とみなすようになったのは、最近のことなのです。

古代では、長さは身体尺と言って、その地方の支配者（国王）の身体を基準に決められていました。古代の日本とエジプトは例外で、その他の地域は世界中どこでも、多くの民族が入り混じっていました。ギリシアも多くのポリスに分かれ、ポリスごとに違った単位系が使われていたのです。たとえば競技場の長さはスタディオンという単位が用いられていましたが、1スタディオンの長さはポリスごとにまちまちでした。つまり、各量ごとに単位 E が設定され、量はその単位 E との“比”として扱われたのです。

アルキメデスの理論でも、長さの場合は長さの単位 E が考えられますが、この E は絶対的な単位の 1 ではなく、そのつど任意に定められ、固定された長さなのです。

古代ギリシア人は無理数を知っていたか

有理数、無理数とは

古代の数学で一番問題となるのは“無限”についてですが、その前に“数”について復習しておきましょう。皆さんの知っている数は、自然数、整数、有理数、実数だと思います。その他に複素数もあります。有理数とは、分母と分子が整数の分数として表される数のことです。有理数でない実数を無理数といいます。

古代ギリシアの数

「ギリシア人は、√2 が無理数であることを知っていた」という表現をときどき見かけますが、これは間違いです。“無理数”という概念は「実数とは何か」が分かっていないと言えないのです。ギリシア人が実際に証明したことは、「正方形の1辺と対角線との比は整数比では表すことができない」ということです。しかし、このことを「ギリシア人が長さを数値で表さなかった理由」にすることはできません。長さだけでなく、重さも、角度も、すべて数値が割り当てられることはなかったからです。

このことはまた、これから述べるアルキメデスの理論を見るとはっきり分かります。円周、円の面積、球の体積などは、“数”として求めるのではなく、正方形とか立方体などの基本となる図形や立体との“比”として求めています。これがアルキメデスの理論を難解なものにしている理由の一つです。

連続量

実数を“連続量”と呼ぶことがあります。この場合の“連続”という概念は現代のものですが、もちろん昔から“つながっている”という意味で“連続”という言葉があります。すると、「数全体は連続である（つながっている）」という主張は、「√2 を数として認めろ！」と強要しているだけのように思われます。というのは、「もし √2 を数として認めないなら、数全体は √2 の所で切れてしまうではないか」と言っているからです。しかし、有理数だけしか数として認めない人にとっては、√2 は数ではないのですから、ここで切れてはいません。

今おこなった議論は、現在の皆さんにとって奇妙に思えるかもしれません。皆さんにとって √2 が数であることなどあたりまえのことだからです。√2 は10進小数で

√2 ＝ 1.414213563…                                             (1)

と表されます。小数点以下数字が無限に続きます。無限ということは、永久に終わりがないことです。このような無限を古代の人が実際に考えたのでしょうか。現在の私たちにとっても、現実の世界でこんな数が実際にあるのでしょうか。無限桁とまでいわなくても、たとえば小数点以下50桁で、単位はメートルでもグラムでもいいですから、この宇宙の中でこのような数値で表されるような実例は存在するのでしょうか。

無限の概念

「自然数は無限個存在する」ことの証明

ギリシア数学で無限に関連した有名な定理として、「素数は無限個存在する」というのがあります。これを簡単にした「自然数は無限個存在する」ことを証明しましょう。

「自然数が有限個しか存在しない」と仮定します。すると自然数の中で最大のものが存在します。これを n としましょう。すると n に１を加えたもの n+1 は n より大きな自然数となります。これは n が最大の自然数と仮定したことに矛盾します。よって自然数は無限個存在することが証明されました。

無限の捉え方

このようにして、ギリシア人は自然数が無限個存在することを示しました。しかしこのことと、上の (1) のような無限列が存在することとは違います。(1) の数字の列は永遠に続き、決して終わることがないのですから。同様のことが、ギリシアの幾何学においてもいえます。ギリシアの幾何における“線”とは、現在の幾何での線分のことで、長さが有限です。ただし、両方向にいくらでも伸ばすことができます。現在の幾何の直線とは、はじめから両方向に無限に伸びています。現在の数学では無限を認めていますし、それならはじめから無限に伸びているとした方が簡潔です。しかし、現実の世界で（無限に伸びた）直線なるものが存在するのでしょうか。

半分にする操作を繰り返すと…

無限の概念がなければ現代数学は成り立ちません。ですから現在の私たちは当然のように無限を受け入れています。ですから古代の人も現代の私たちと同じように無限を見ていると思いがちです。しかし、古代の人の持つ無限の概念は、現代の私たちのものとは違うかも知れないのです。また、現代においても無限に対する考え方が少し変わってきているのかもしれません。

「半分にする」操作を考えてみましょう。1/2 を2回繰り返すと 1/4、3回繰り返すと 1/8、となります。n回繰り返すと

となります。次はよく使うので覚えておきましょう。

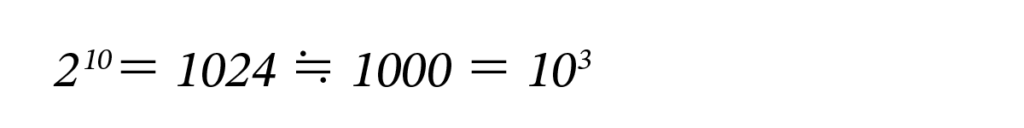
したがって、

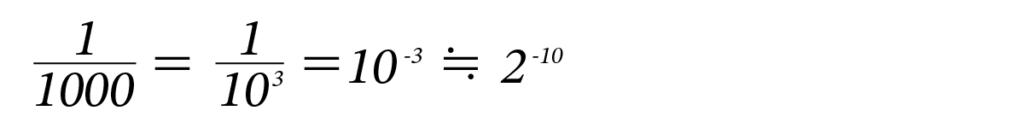
となります。つまり、半分にする操作を10回繰り返すと、1/1000 となります。

単位を 1m (メートル)とします。10^-9 m ＝ 1ナノメートルです。

原子の大きさは 10^-10 m、　素粒子の大きさは 10^-18 m

現在の物理学者は 10^-18 m あたりが長さの最小値だと考えているようです。時間に関しては、これよりはるかに小さい最小値を取ります。かつて、量子力学の大家ハイゼンベルクは、10^-26 秒あたりではないかと説きましたが、現在では 1プランク時間 ＝ 10^-43 秒 となっています。つまり、これより小さな時間はなく、ここまでくると、過去・現在・未来　がふらふらしているようです。

現実の世界における「無限」とは？

数学の世界では、任意の n に対し 1/2ⁿ という数が存在しますが、現実の世界では「半分に割る操作」はすぐに限界にきてしまいます。また、上で「 √2 の小数点以下 50桁までを必要とするような、現実の世界の具体例が存在するのか？」を考えました。このような実例はなかなか見つかりそうにありません。

この宇宙に外接するような立方体を考えましょう。すると、立方体の1辺の長さは 10²⁵ m あれば十分です。側面の正方形の対角線の長さは、√2 の小数点以下40桁あれば、原子の大きさ以内の誤差で表せます。ちなみに、現在の物理学では、この宇宙は有限であるという説も有力です。私たちを取り巻く世界は有限で、無限という概念は数学の世界だけに存在するのかもしれません。

アルキメデスは”無限”をどのように考えていたのでしょうか。次回は、アルキメデスの時代、古代ギリシアでは「数」をどのように扱っていたのか、数学の基本的な概念の一つである数列について詳しく見ていきましょう。