2-3 πの源流

 

現在の私たちは分数も小数も自由に使いこなしています。そして“数”はあまりにも基本的なので、世界史にその名を残した大数学者のアルキメデスが、今では小学生でも知っている分数を使いこなせていなかったなどとは信じがたいと思うでしょう。しかし考えてみると、量における掛け算とか割り算の意味はなかなか難しいのです。たとえば“重さ×重さ”とか“時間×時間”に何か意味があるのか、すぐには思いつきません。“長さ÷時間（速度）”とか“重さ÷体積（比重）”のような量の掛け算や割り算を考えるようになったのは、近世に入ってからです。量を数として認識し、自由に四則演算ができるようになったのは、アルキメデスのような天才が多くの知見を遺してくれたおかげなのです。本節では古代ギリシアのアルキメデス が円周率をどのように考えていたかを調べてみましょう。

古代における比とは

現在の皆さんは、“比”を「分数の表現方法の一つ」と思っているかも知れません。現在ではそれでよいのですが、古代では比と分数はまったく違うものでした。“現在の比”と“分数”になれている皆さんにとっては、“古代の比”を理解するのはなかなか難しいと思います。本来なら、ここで述べる円周率には、比についての厳密な定義の後にするべきなのですが、あえて先に持ってきました。比の厳密な扱いは『原論』によって始めてなされました。しかし、ユークリッド※が『原論』を書くはるか昔から、バビロニアやエジプトで“比”は実用的な問題を解く道具として用いられてきました。これは、19世紀になって「実数の厳密な定義」がなされるずっと前から、ニュートン※やガリレオ※など多数の人がすでに数を使っていたのと同様です。

円周率とは何か

無限とは何か

アルキメデスが円周率 π の近似値として次の近似値を得たことは有名です。

\( 3\frac{10}{71} < \pi < 3\frac{1}{7} \quad 　(1)\)

“近似値”とは“真の値”に近い値ということです。アルキメデスははたしてこのような“真の値”なるものを考えていたでしょうか。現在の私たちは π の値が小数点以下無限に続くことを知っています。無限とは1億桁でも100億桁でもなく、無限に続くのです。はたしてそんな数が存在するのでしょうか。存在するかどうかはともかく、π が存在しなければ現在の数学そのものが存在しなくなってしまいます。しかし、アルキメデスが得たのは (1) のような数値ではなく“比”だったのです。

アルキメデスの考えた”円周率”と現在の”円周率の定理”

円周率とは「直径に対する円周の比」のことですが、現在では

円周率π ＝ 直径 R の円の円周 / R

の値として用いられています。ギリシアでは“比”とは「2つの量の間の関係」のことで、分数とか小数などの数値としては扱うことはありませんでした。(1) を比の形で表すと

223r : 71r ＜ 〇(r) : 2r ＜ 22r : 7r                               (2)

となります。ここで r は線分で、〇(r) は、半径 r の円の円周を表します。2つの比 a：b と c：d の間には、次節で述べるように、大小関係 “＜” と同値関係（等価性） “＝” が定義されます。アルキメデスが理論を展開する上で使用したのは (2) の形の比例式ではなく次の定理です。

この定理のように、比の理論では「～は…に比例する」という表現がよく使われます。「円周は半径に比例する」という表現の本来の意味は式 (3) なのです。古代では比は常に2つの比 a : b と c : d が“等しい”とか“大きい”かを議論し、常に4つの対象 a, b, c, d が現われます。現在では、円周率の定理は

〇(r)/r ＝ 一定値 π

と表現され、考え方がとてもシンプルになりました。

アルキメデスの証明

(2) の証明は〔Web連載ピラミッドの秘密〕で述べました。円周率の定理も、その証明からただちに得られるので、ここではその証明の概略を現代の用語を用いて説明することにします。アルキメデスは、半径 r の円 O の円周の下界と上界を、円 O に内接する正 n 角形(図2.3.1 (a))と、外接する正 n 角形(図2.3.1 (b))を考えることで計算しました。

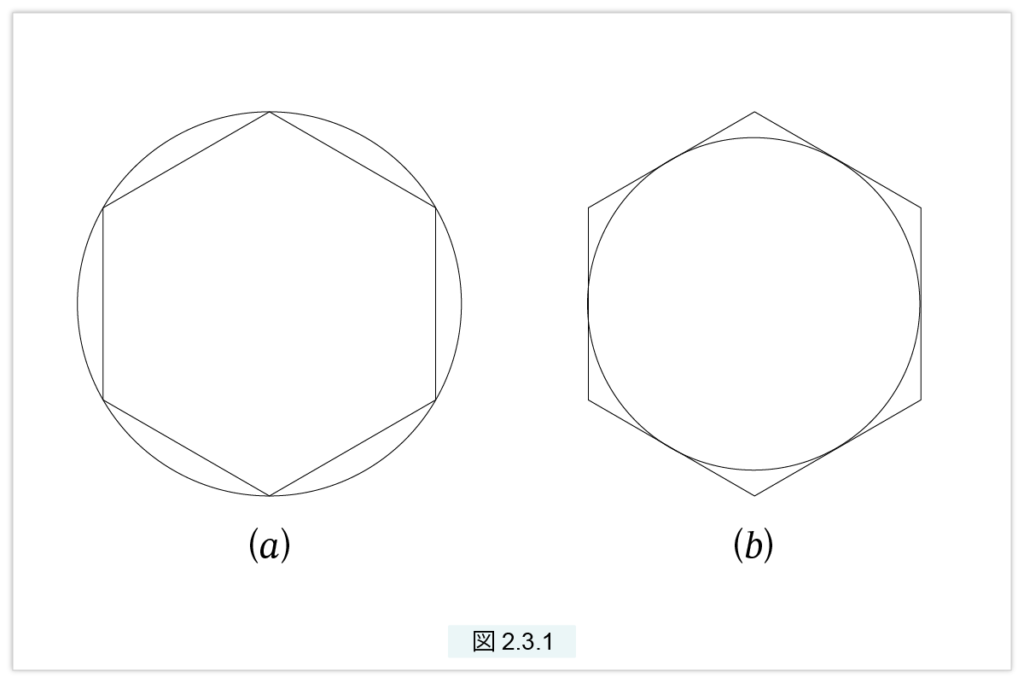
正6角形から始め、正12角形、正24角形、正48角形と計算を進め、最終的に正96角形まで計算を進めました。現在のコンピュータなら、正96角形を書くことは容易です。実際に書いてみると、人間の見た目にはほとんど円と見分けがつきません。

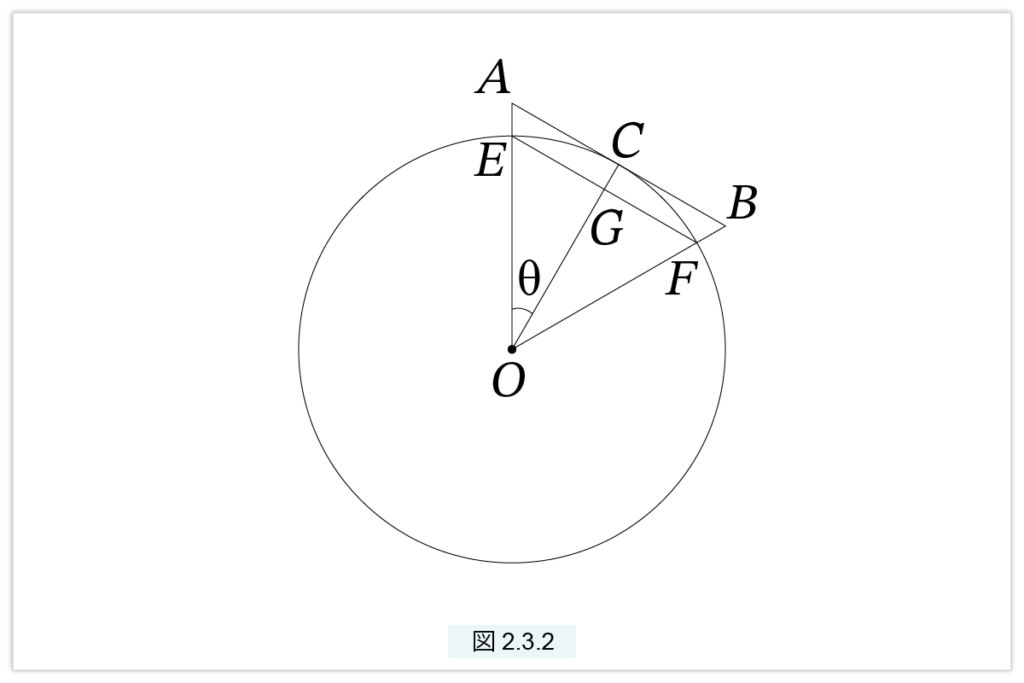
図2.3.2 において、辺 AB は外接正n角形の1辺、EF は内接正 n 角形の1辺です。明らかに

辺EF ＜ 弧ECF ＜ 辺AB

辺々を n 倍すると

内接n角形の周長 ＜ 円周 ＜ 外接n角形の周長                              (4)

となります。現代では OC＝OE＝1 として計算します。∠AOC＝θ と置くと、

\( EG ＝ sin\theta, \quad AC ＝ tan\theta \)

となります。三角関数をまだ知らない人は、sin と tan は次の比（分数）のことだと思ってください。

\( sin \theta = \frac{EG} {OE} , \quad tan \theta = \frac{AC} {OC}\)

アルキメデスは三角関数という概念はまだ持っていませんでしたが、もちろんこのような比は使いこなしていました。正96角形の場合、n＝96 ですから

\( \theta = \frac{360°}{2n} = 1.875度 \)
\( sin1.875 = 0.032719, \quad tan1.875 = 0.0327366 \)

となります。半径を1 としましたから、円周率は半円の長さです。内接正96角形と外接正96角形の周長の半分は

96×sin 1.875 ＝ 3.1410 ＞ 223/71 ＝ 3.1408
96×tan 1.875 ＝ 3.1427 ＜ 22/7 ＝ 3.1486

となり、223/71 と 22/7 は共によい上界と下界であることが分かります。

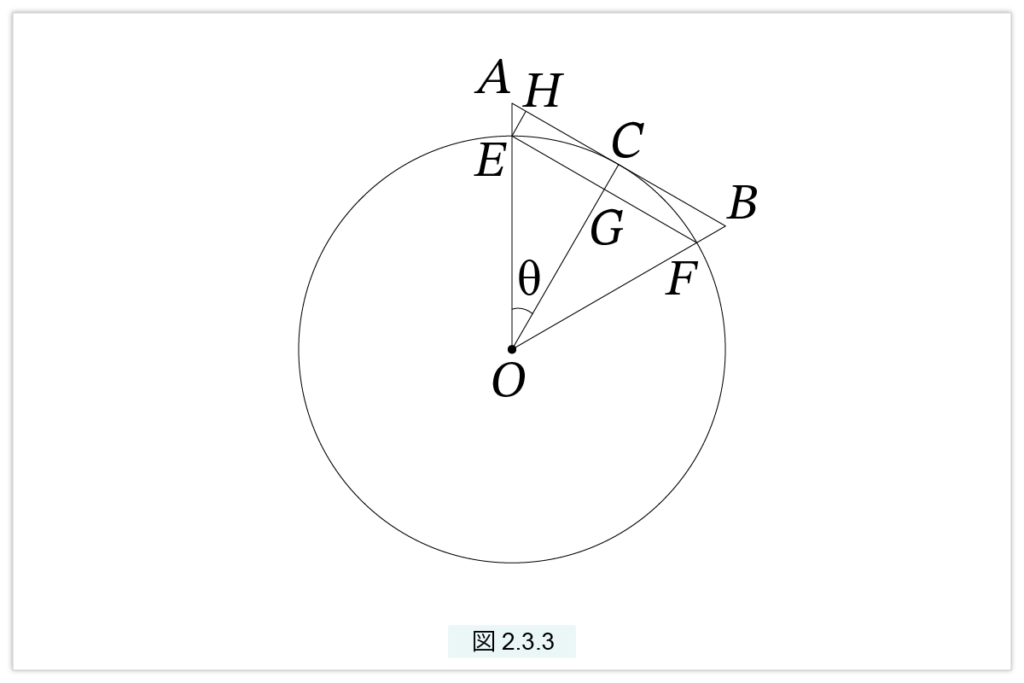
n を大きくしていくと、内接正 n 角形と外接正 n 角形がどんどん円周に近づいていくことが、直観的には理解できます。しかし、これを数学的に証明する必要があります。図2.3.3 より、

外接n角形の周長 – 内接n角形の周長 ＝ 2n × AH

です。∠AEH ＝ θですから、△AEH を n 個集めると、半径 EH の円に外接する正 n 角形（または、半径EA の円に内接する正 n 角形）になります。また、

\( EH ＝ GC ＝ OC – OG ＝ 1 – cos\theta \)

ですから、θ が0に近づくと、EH も0 に近づき、EH に外接する正 n 角形の周長も 0 に近づきます。したがって、n を十分大きくとれば

外接 n 角形の周長 – 内接 n 角形の周長 は 0 に近づく                          (5)

ことがわかります。

円周率の定理を証明する

古代ギリシアの幾何学とは

さて、上でおこなった議論のどこが古代の数学として許されないかを検討しましょう。まず、図2.3.2 で、OC の長さを 1 としました。現在では、長さは1メートル、重さは1グラムと、単位の長さ、単位の重さを用います。しかし、古代ギリシアの幾何学ではこのような普遍的な単位を用いることはありません。常に暫定的に定めた長さを基準とします。たとえば上での議論では、OC ＝1 とはせず、OC をある固定された線分 r とします。したがって、辺AC とか EG の“長さ”とは、アルキメデスの議論の中では長さ自身ではなく“r との比”として扱われていました。円周率の議論では、最初正六角形から始めます。図2.3.2 で言うと ∠AOC ＝ 30度 です。現在の議論では、OC＝1 とすると、AC ＝ 1/√3 となります。アルキメデスは議論の中で、このように長さを数値で表すことはありません。長さは常に r との比で表します。この場合は、OC : AC を √3 : 1 を近似する“整数の比”として表しています。

アルキメデスの理論を古代の比の理論だけで行うと、とても難解なものとなります。したがって、〔ピラミッドの秘密〕では比を分数に置き換えて議論しています。しかし、数学がどのように発達をしてきたかを見るためには、当時の比の扱い方を正しく理解しなければなりません。当時の比の扱いを知るには“当時は何ができなかったか”を知ることが近道です。

円周率の定理の証明

さて、〔円周率〕の定理である式(3) の証明をしましょう。(3) は次のように書き換えられます。

〇(r₁) : r₁ ＝ 〇(r₂) : r₂                                                (6)

つまり、円周 〇(r) と半径 r の比は、半径 r によらず一定である、ということです。

比とか“相似”は、古代エジプトでもバビロニアでも、いろいろな問題を解くのに使われていました。2つの図形は、拡大とか縮小をして、ぴったりと重ね合わせることができるとき“相似”といいます。明らかに2つの円は相似です。しかしこれは“相似”の正式な定義ではありません。エジプトでもバビロニアでも (3) とか (6) が事実であることを知っていたと思います。皆さんは、「明らかな事実は証明する必要はない」と思いますか。ギリシアで発展した「論証数学」では、そのようには考えませんでした。どのように明らかだと思われる事実であっても、公理以外のものは証明しなければならなかったのです。

これから (6) を証明するのですが、比の理論のこのような証明が初めての人にとっては、以下の証明はとても難解だと思われるので、まず直観的な説明をしておきます。この部分は読み飛ばしても結構です。まず (6) の意味は、「○(r)/r, つまり“半径 r の円周÷r”は、どんな r に対して常に 2π となる」ということで、これは皆さんご存知だと思います。(6) が成り立たないということは ○(r₁)/r₁ ≠ ○(r₂)/r₂ となる r₁ と r₂ が存在するということです。存在すると仮定して矛盾を導きます。半径 r の円に外接する正多角形と内接する正多角形の「周長/r」は、r によらず、いくらでも 2π に近づくことを使って矛盾を導きます。

さて (6) を証明しましょう。2つの正 n 角形は相似です。半径 r の円に内接する正 n 角形の周長を Q(r, n)、外接する正 n 角形の周長を P(r,n) と書くことにしましょう。すると、任意の r₁ と r₂ に対して次が成立します。

Q(r₁,n) : r₁ ＝ Q(r₂,n) : r₂                                             (7)
P(r₁,n) : r₁ ＝ P(r₂,n) : r₂                                              (8)

(6) が成立しなかったと仮定します。皆さんは比に不慣れと思われますから、分数で表わすことにしましょう。

\( \frac{〇(r_1)}{r_1} ＜ \frac{〇(r_2)}{r_2} \)                                 (9)

であったとしましょう。つまり、この2つの比（分数）の間には隙間があります。一方上で述べた (4) を記号で書くと

\( Q(r,n) ＜ 〇(r) ＜ P(r,n) \)

よって

\( \frac{Q(r,n)}{r} ＜ \frac{〇(r)}{r} ＜ \frac{P(r,n)}{r} \)

となります。この r は任意の半径なので、r₁ と r₂ に対しても成立します。よって、次が成立します。(7)より Q(r₁,n)/r₁ は半径 r₁ に依存しないので、r としました。P(r₁,n)/r₁ についても同様です。

\( \frac{Q(r,n)}{r} ＜ \frac{〇(r_1)}{r_1} ＜ \frac{P(r,n)}{r} \)
\( \frac{Q(r,n)}{r} ＜ \frac{〇(r_2)}{r_2} ＜ \frac{P(r,n)}{r} \)

(5) より、Q(r,n)/r と P(r,n)/r はいくらでも近づけることができます。これは (9) に矛盾します。したがって (6) が成立しなければなりません。

ここでおこなった円周率の定理の議論には“無限”の概念はでてきていません。また、無限に繰り返す操作もありません。おそらくアルキメデスの時代にはまだ「比 〇(r)：r の値」という概念には至っていなかった、と思われます。