3-5. 三角形分割による求積

本節では、アルキメデスが考えた方法で放物線の切片の面積を求めます。アルキメデスは数学の分野で様々な業績を残しましたが、この「三角形分割による求積」の方法も有名で、後世に大きな影響を与えました。この方法は前節で考えた定理を利用しますので、証明に使用する定理について詳しく知りたい方は〔3-4. 斜交座標〕をご一読ください。

等比数列

無限級数

次の数列は本シリーズでもよく登場する歴史的に有名な数列です。

\( 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \cdots \)　　(1)

この数列は、次々に前の項の半分になっています。これらの項をすべて足した和

\( S = 1 + \frac{1}{2} + \frac{1}{4} + \cdots + \frac{1}{2^n} + \cdots\)　　(2)

を、数列 (1) の無限級数といいます。近世になって、数学が進歩してくると無限級数が頻繁に用いられるようになります。アルキメデスははたして“無限級数”というようなものを考えていたのでしょうか。これを頭の隅において、この節をお読みください。

等比数列

(1) に現れる数は分数ですから、古代ギリシアにはありません。アルキメデスが扱ったのは、量の列

\( a_1, a_2, a_3, \cdots \)　　(3)

です。量の列 (3) が等比列であるとは、隣り合う項の比がすべて等しいこと、つまり

\( a_1 : a_2 = a_2 : a_3 = a_3 : a_4 = \cdots \)

が成り立つときのことをいいます。 現在では、量も数として扱っていますから、等比列ではなく等比数列といいます。また、少し古い言い方では、幾何数列と呼ぶこともあります。

アルキメデスは、

\( a_i : a_{i+1} = 4 : 1, \hspace{10pt} i = 1,2, \cdots \)

つまり

\( a_{i+1} = \frac{1}{4} a_i, \hspace{10pt} i = 1,2, \cdots\)

で定義される量の列 a₁, a₂, a₃,… を扱っています。この第 n項までの和 V_n は現代の式で表すと

\( V_n = a + \frac{1}{4}a + \left( \frac{1}{4}  \right) ^2 a + \cdots + \left( \frac{1}{4}  \right)^n a \hspace{20pt} (a=a_1) \)

となります。

補助定理 – 等比列

アルキメデスは次を証明しています。

補助定理の証明〈アルキメデスの方法〉

現代の私たちはこういった証明は数学的帰納法を使うのですが、アルキメデスは n＝5 の場合を示しています。私たちも n＝4 でやってみましょう。まず

4a₄ = a₃,　4a₃ = a₂,　4a₂ = a₁

ですから、

3×(a₁＋a₂＋a₃＋a₄)＋a₄
＝ 3×(a₁＋a₂＋a₃)＋3a₄＋a₄
＝ 3×(a₁＋a₂＋a₃)＋4a₄
＝ 3×(a₁＋a₂＋a₃)＋a₃
＝ 3×(a₁＋a₂)＋3a₃＋a₃
＝ 3×(a₁＋a₂)＋a₂
＝ 3a₁＋3a₂＋a₂ ＝ 3a₁＋a₁ ＝ 4a₁

となり成立します。

三角形分割による切片の求積 – 放物線の切片の面積

【定理】三角形分割による切片の求積

以下では放物線の切片の面積を、アルキメデスの独創的な方法で求めます。図3.5.1 を見てください。

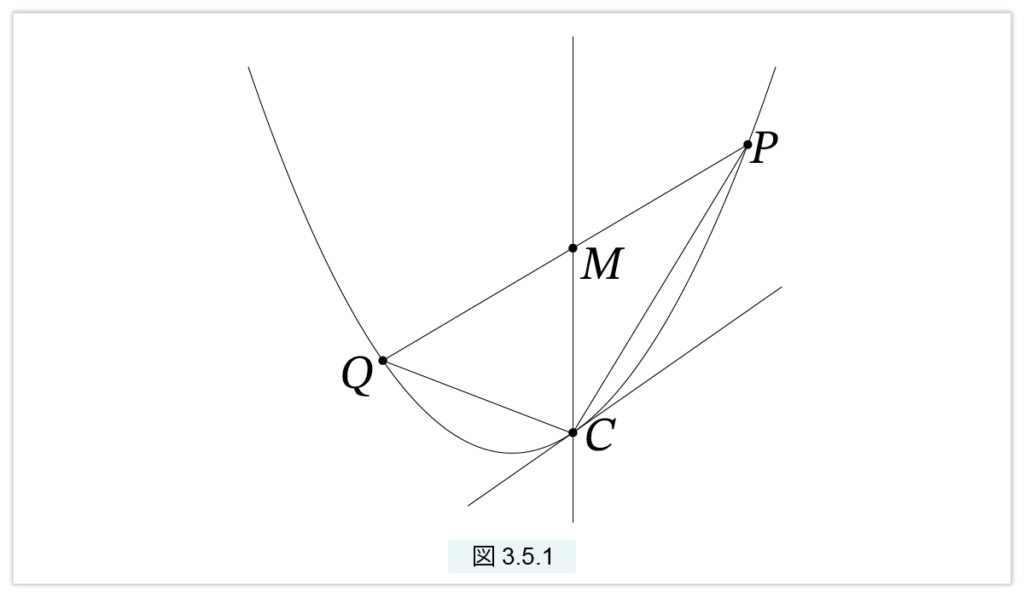
P, Q を放物線上の点とし、切片PQ の面積を求めます。この切片の“高さ”とは放物線上の点で線分 PQ から最も離れたところにある点のこととします。その点とは、PQ に平行な放物線の接線の接点になります。その接点を C とします。すると 3-4. 斜交座標 の 〔軸と切片中点 の定理〕より、Cを通る中心軸に平行な直線は PQ の中点を通ります。しかし、PC に平行な接線はこの C を通る接線以外にはありません。したがって逆に、PQ の中点を M とし、M を通る中心軸に平行な直線を引き、放物線との交点を C とすれば、C を通る PQ に平行な直線は放物線の接線となります。

以下では次の定理を証明します。

【定理】三角形分割による切片の求積 の証明

証明のため、図3.5.1 の記号 P, Q, M, C に添え字をつけ P₁, Q₁, M₁, C₁ とします（図3.5.2 ）。また、P₁ における接線と M₁C₁ の延長線との交点を R₁ とすると、 3-4. 斜交座標 の〔斜交座標の接線〕の定理より、M₁C₁＝C₁R₁ となります。上で行った議論と同様に、P₁ を通る接線はこれ以外にはありません。したがって逆に、M₁C₁ の延長線上に点 R₁ を、M₁C₁＝C₁R₁ となるようにとると、P₁R₁ は放物線の接線となります。同様の理由によって、Q₁R₁ も放物線の接線となります。

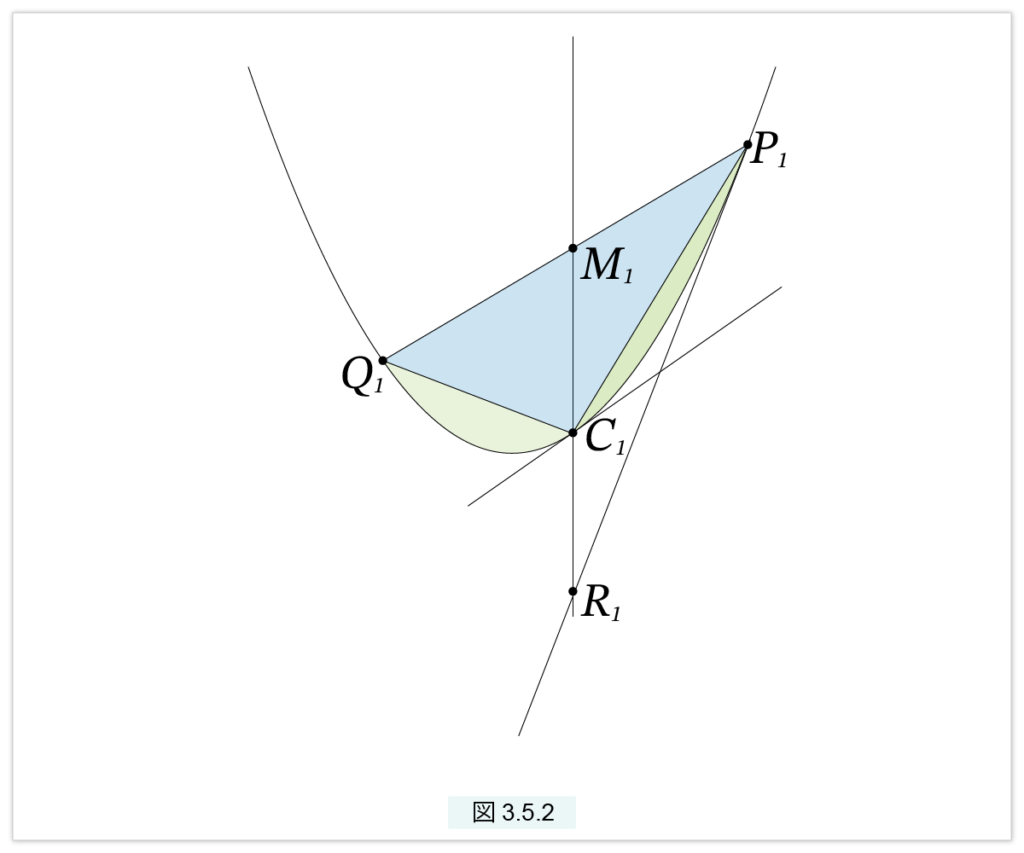
これで、放物線の切片を求める準備が整いました。次が成立します。

切片P₁Q₁ ＝ △P₁C₁Q₁ ＋ 切片P₁C₁ ＋ 切片Q₁C₁                                (5)

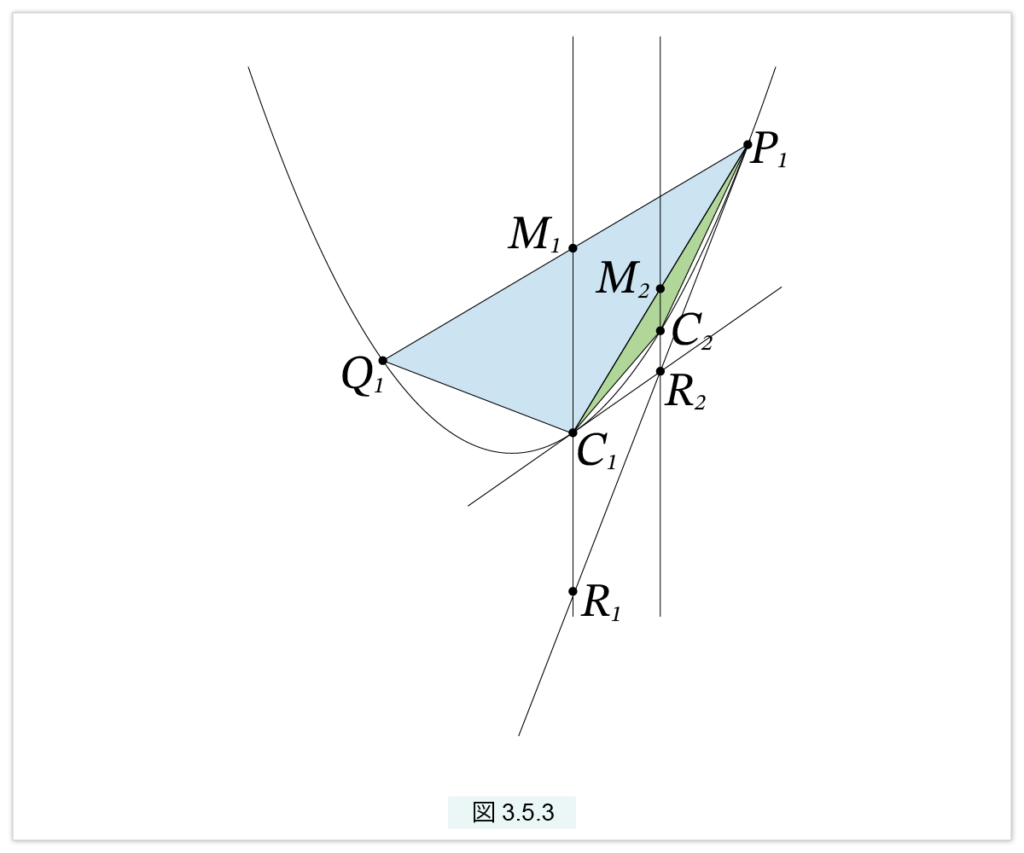
切片P₁C₁ と 切片Q₁C₁ についても 切片P₁Q₁ と同じことを行います。切片Q₁C₁ は 切片P₁C₁ と同様です。P₁C₁ の中点を M₂とし、M₂ を通る中心軸に平行な直線と放物線との交点を C₂, とします（図3.5.3）。また、M₂C₂ の延長線とP₁R₁ との交点を R₂ とします。すると〔斜交座標の接線〕の定理より、P₁R₁ が接線であることから

M₂C₂ ＝ C₂R₂

が成立します。またC₁R₂ は C₁ における接線であり、P₁Q₁ と平行です。ここで、

T₁ ＝ △P₁C₁Q₁,　　T₂ ＝ △P₁C₂C₁

と置き、T₁ と T₂ の大きさを比べます。

M₁ は P₁Q₁ の中点、C₁ は M₁R₁ の中点だから

T₁ ＝ △P₁C₁Q₁ ＝ 2△P₁M₁C₁ ＝ 2△P₁C₁R₁

△P₁C₁R₁ と △P₁M₂R₂ は相似で M₂ は P₁C₁ の中点、C₂ は M₂R₂ の中点だから

△P₁C₁R₁ ＝ 4△P₁M₂R₂ ＝ 8△P₁M₂C₂ ＝ 4△P₁C₂C₁ ＝ 4T₂

となります。以上を合わせると

T₁ ＝ 8T₂  したがって　\( T_2 = \frac{1}{8}T_1 \)

が得られます。まったく同様にして、切片Q₁C₁ にも T₂ と同じ面積の三角形が現われます。（図3.5.4）

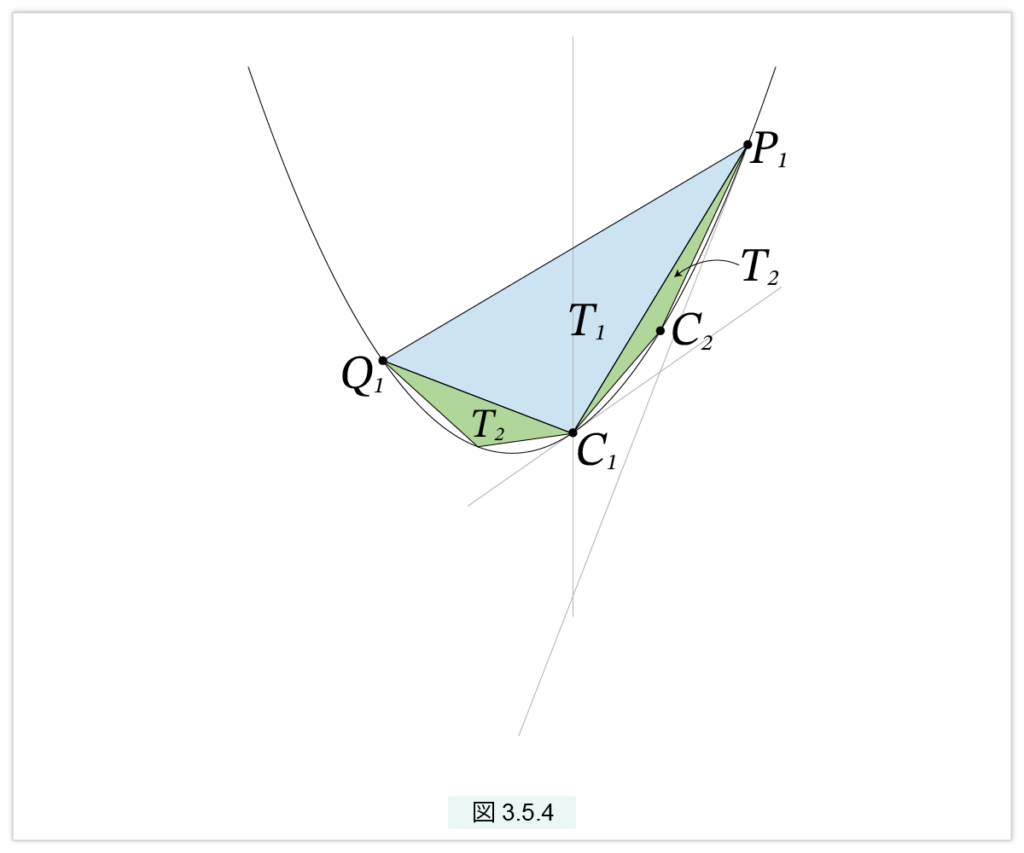
次に処理しなければならない切片は4つです。これらの切片のなかにできる三角形の面積を T₃ とすると、いまと同様の議論により

\( T_3 = \frac{1}{8}T_2 \)

となります。これを続けると、切片PQ は三角形 T₁, T₂, T₃, … で覆い尽くされます。ただし、T₁は1個、T₂ は2個、 T₃ は4個 … と次の小三角形の個数は倍に増え、面積は 1/8 となります。したがって、

切片PQ = T₁ + 2T₂ + 4T₃ + …
= T₁ + 2 \( \cdot \frac{1}{8} \cdot \) T₁ + 2² \( \cdot \left( \frac{1}{8} \right)^2 \cdot \) T₁ + …
= T₁ \( \left\{ 1 + \frac{1}{4} + \left( \frac{1}{4} \right)^2 + \cdots \right\} = \frac{4}{3} \) T₁
= \( \frac{4}{3} \) △PQC

となります。しかし、この式は無限級数であり、現在のやり方です。切片PQ が三角形で覆い尽くされ、直観的には分かりやすいのですが“無限の手続き”を必要とします。

【定理】三角形分割による切片の求積 の証明 ＜挟み撃ち＞

アルキメデスのとった方法を見てみましょう。アルキメデスがいつも使う方法は挟み撃ち論法です。

S₁ ＝ 切片P₁Q₁,　S₂ ＝ 切片P₁C₁,　S₃ ＝ 切片P₁C₂, …

と置きます。（図3.5.5）

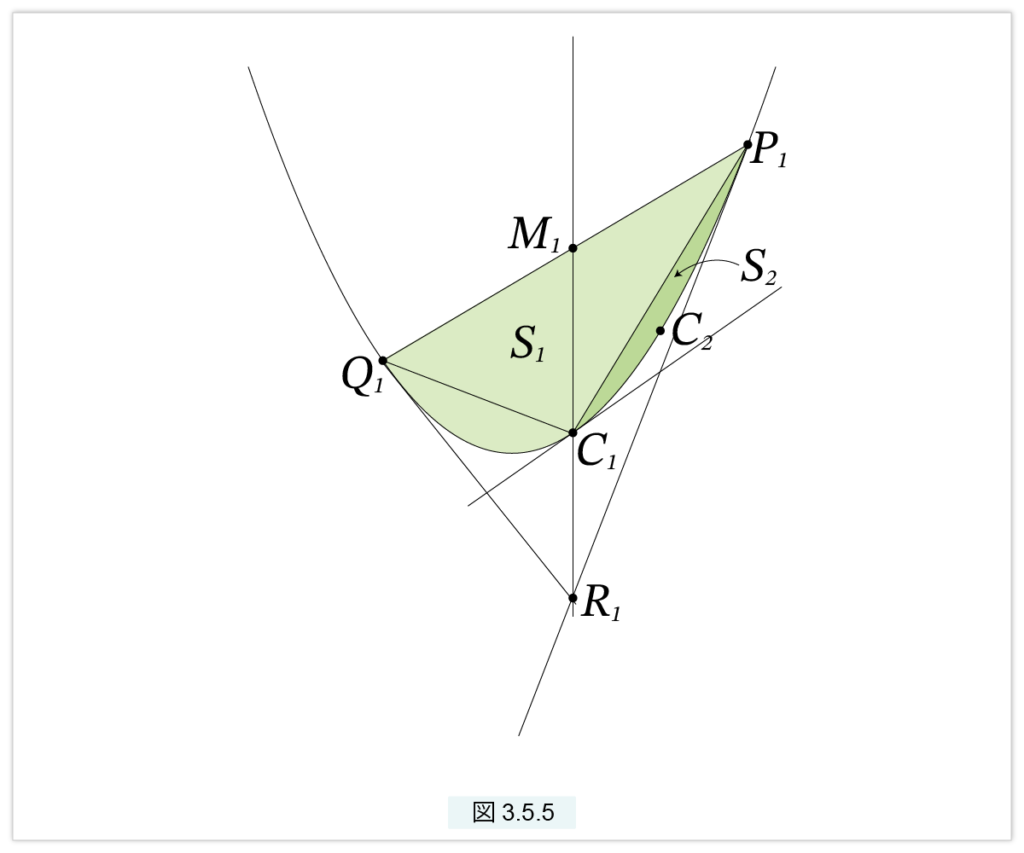
切片 S₁ の内接三角形は T₁ ＝ △P₁C₁Q₁ で外接三角形は △P₁R₁Q₁ ですが C₁ は M₁R₁ の中点ですから

T₁ ＜ S₁ ＜ 2T₁

が成り立ちます。下界と上界を縮めていきます。切片 S₁ は三角形 T₁ と2つの切片 S₂ の和ですが、S₂ に対しても T₂ ＜ S₂ ＜ 2T₂ が成り立ちますから、

S₁ ＝ T₁＋2S₂ ＞ T₁＋2T₂
S₁ ＝ T₁＋2S₂ ＜ T₁＋4T₂

となります。これを続けると、

T₁ + 2T₂ + … + 2^n-1 T_n ＜ S₁
＜ ( T₁ + 2T₂ + … + 2^n-1 T_n) + 2^n-1 T_n　　(6)

上の補助定理を適用するために

a_i = 2^i-1 T_i

と置きます。すると、

a_i : a_i+1 = 2^i-1 T_i : 2ⁱ T_i+1 = T_i : 2 T_i+1 = 4 : 1

となり、補助定理の条件を満たします。補助定理を適用するため、(6)式を3倍します。

3 × (T₁ + 2T₂ + … + 2^n-1 T_n )＜ 3S₁
＜ 3 × (T₁ + 2T₂ + … + 2^n-1 T_n ) + 3 ×2^n-1T_n 　　(7)

すると

3 × ( T₁ + 2T₂ + … + 2^n-1 T_n )
= 3 × ( a₁ + a₂ … + a_n ) = 4a₁ – a_n 　　(8)

3 × ( T₁ + 2T₂ + … + 2^n-1 T_n ) + 3 × 2^n-1 T_n
= 3 × ( a₁ + a₂ … + a_n ) + 3 × a_n
= 4a₁ – a_n + 3a_n = 4a₁ + 2a_n　　(9)

となります。(7), (8), (9) をまとめると、

4a₁ – a_n ＜ 3S₁ ＜ 4a₁ + 2a_n

となります。

a₁, a₂, … は毎回 1/4 になり、 a_n はいくらでも小さくできますから

3S₁ ＝ 4a₁

となります。S₁ は切片PQ で、a₁ ＝ T₁ は △PQC ですから、

切片PQ : △PQC ＝ 4 : 3

が得られます。

無限の概念について

このアルキメデスの論法には“無限”の概念は使われていません。使われているのは「a_n がいくらでも小さくできる」という事実だけです。現在の“無限級数”を使った議論は、下界と上界の差がいくらでも小さくできるという“挟み撃ち論法”を使う必要がなくなり、分かりやすくなっています。無限級数は、アルキメデスの理論から生まれた概念ではあるにしても、アルキメデスの時代にはまだなかったのです。

“アルキメデスほどの人が無限を知らないはずはない”という記述をよく見かけます。もちろん、アルキメデスは「例えば自然数が無限に存在する」ことは知っていました。しかし、このことと無限級数とは“無限の扱い方”が違うのです。無限級数とは“決して終わらない物語（数列の和）”であり、近世に入ってから作られた概念なのです。