小石の数理
アルキメデスの面積と体積
放物線の求積
3-4. 斜交座標とは? | アルキメデスの求積の要となる定理を解説
ページ目次
放物線と座標
古代の放物線
現在の私たちは放物線といえば常にXY座標を頭に浮かべ、放物線上の点 P は座標として、実数の組 (x, y) で与えられます。放物線の描き方も決まっていて、放物線の頂点が原点になかったり、放物線が横を向いていたりしたら、すべて違ったものとして扱われます。一方古代では、向きは自由ですし、2本の軸は直交している必要はありませんでした。このような座標を斜交座標といいます。放物線もこの斜交座標で表されます。
直交座標
まず直交座標、つまり XY座標の復習をしましょう。古代では軸の向きは自由だと言いましたが、本連載では軸の向きは鉛直と水平に固定して、鉛直軸と水平軸と呼ぶことにします。点 P を表す組 (x, y) は、古代では座標ではなく辺の長さです( 図3.4.1 )
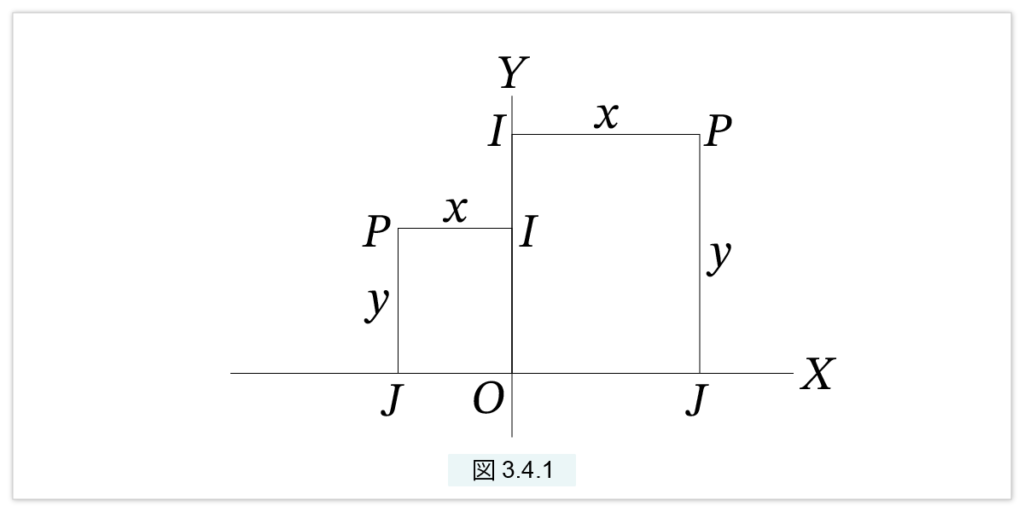
点 P から鉛直軸に下ろした垂線の足を I、水平軸に下ろした垂線の足を J とします。PI の長さが x で、PJ の長さが y です。図が示すように、P は水平軸の上側しか許されませんが、鉛直軸に関しては右と左の両方が許されます。以下の議論では、鉛直軸の右側の P についてだけ説明しますが、左に現れる P についてもまったく同様の事柄が成立します。
斜交座標
2つの軸が任意の角度で交わる座標が斜交座標です。古代では軸の向きは自由ですが、本書では1本を鉛直に固定し、もう一方を斜交軸と呼ぶことにします。点 P は斜交軸の上側にしか許されませんが、鉛直軸に関しては両側に許されます。
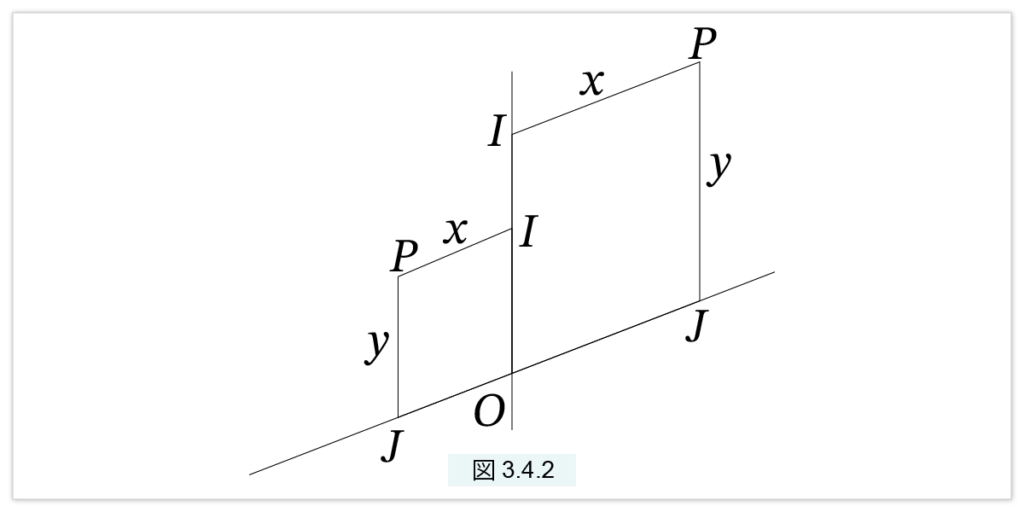
図3.4.2 で、PI は斜交軸に平行、PJ は鉛直軸に平行です。直交座標と同様、点P を辺の組 (x, y) で指定します。PIとJO、PJとIO は平行になるので、PIOJ は平行四辺形となります。したがって、PJ=IO=y です。図が煩雑になることを避けるため、線分 PJ を書かずに、IO で y を表すことがあります。
本節では、この斜交座標で放物線が
□(p, y) = □2(x)
と表されることを示します。ここで p は長さを表すだけの固定された線分ですが、図には現れないこともあるので注意してください。この定理を〔斜交座標〕定理と呼びます。読者の皆さんは、(x, y) は座標と、□(a, b) は a と b の積 a·b と、比 a : b は割り算 a/b とみなしてかまいません。このように解釈すると、以下の議論が読みやすくなると思います。
斜交座標の定理
何のための定理か
アルキメデスは独創的な方法で放物線の切片の面積を求めています。本節ではいくつかの定理について述べますが、「これらはいったい何のための定理なのか?」「求積というタイトルなのに面積を求める話はどこへいった?」と思う方がいるかもしれません。一見道筋がわかりづらいように感じますが、アルキメデスはこれらの定理を使って非常に鮮やかな方法で放物線の切片の面積を求めているのです。
定理の証明には、前節までに紹介した定理を使っている部分があります。既出の定理については解説を省いているため、本節だけではわかりづらいところがあるかもしれませんが、おおまかな流れを掴んでいただければと思います。
補助定理
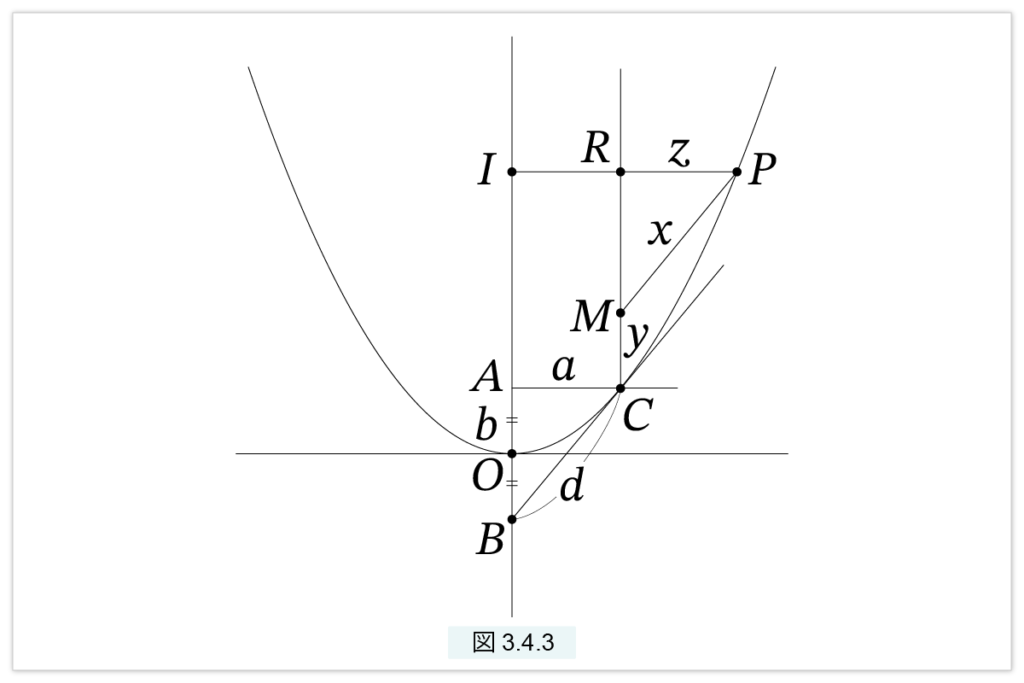
図3.4.3 の放物線を考えます。CB は放物線の接線です。これまで放物線は、頂点と、頂点を通る中心軸を基準として考えてきましたが、アルキメデスは視点を自由に動かし、放物線上の任意の点 C を固定し、C を通る接線を斜交軸、C を通る鉛直線を鉛直軸とした斜交座標を考えます。M は鉛直線上の点、PM は斜交軸に平行な直線です。この放物線を
□(p, IO) = □2(IP)
とします。p は固定された線分、P は放物線上の任意の点、O は放物線の頂点、I はP から中心軸に下ろされた垂線の足です。A を C から中心軸に下ろした垂線の足とし、AC=a, AO=b とおくと
□(p, b) = □2(a) (1)
が成立します。CB は放物線の接線ですから、
AB = 2AO = 2b (2)
さて、P は放物線上の任意の点でした。R を PI上に図のように取り、線分 PR, PM, MC に次のように記号を割り当てます。
\( PR=z, \quad PM=x, \quad MC=y \)
次は、この節の主定理を証明するための補助定理です。
【補助定理】
図3.4.3 において次が成立する。
□(p, y) = □2(z)
ー 補助定理の証明 ー
以下の式の変形では、□(u, v) を現代の uv に変形すれば容易に理解できます。
IP = a+z ですから、
□2(IP) = □2(a+z) =□2(a)+2□(a,z)+□2(z) (3)
△PRM と △CAB は相似だから (2) より
z : RM = CA : AB = a : 2b = □(p, a) : 2□(p, b)
= □(p, a) : 2□(a, a)= p : 2a
よって、内項の積=外項の積 を最初と最後の式に適用すると、
□(p,RM) = 2□(a,z)
となります。またこの式と、IO= RM+MC+AO より
□(p,IO) = □(p,AO+MC+RM)
= □(p,AO)+□(p,MC)+□(p,RM)
= □2(a)+□(p,y)+2□(a,z)
が得られます。放物線 □(p, IO) = □2(IP) と (3) と今得た式より、
□2(a)+2□(a,z)+□2(z) = □2(IP)= □(p, IO)
= □2(a)+□(p,y)+2□(a,z)
が得られます。よって、
□2(z) = □(p,y)
が成立します。
【定理】斜交座標
次に〔斜交座標〕定理 を証明します。( 図 3.4.3 再掲)

【定理】斜交座標
図 3.4.3 において線分 r が存在し、放物線上の任意の点 P に対し次が成立する。
□(r, y) = □2(x)
ー 【定理】斜交座標 の証明 (分数を使った証明) ー
CB=d と置きます。まず、現代式に比ではなく分数を使って証明します。△PRM と △CAB は相似だから、
z = \( \frac{a}{d} x\)
と表せます。補助定理 で得た方程式 py = z2 に代入すると、
\( py = \frac{a^2}{d^2} x^2 \)
\( \frac{pd^2}{a^2} y = x^2 \)
よって、r = \( \frac{pd^2}{a^2} \) と定めると ry = x2という結果が得られます。
ー 【定理】斜交座標 の証明 (比を使った証明) ー
比を使って証明し直しましょう。p, a, d は固定された辺なので、
r : p = □2(d) : □2(a)
を満たす辺 r が存在します。△PRM と △CAB は相似だから
d : a = x : z
が成立します。よって〔比の自乗則〕より
□2(d) : □2(a) = □2(x) : □2(z)
となります。よって、
□(r, y) : □(p, y) = r : p
= □2(d) : □2(a) = □2(x) : □2(z)
が成立します。上で示した 補助定理より
□(p, y) = □2(z)
ですから、定理〔右項の一致〕を使って、
□(r, y) = □2(x)
が成立します。
軸と切片中点、斜交座標の接線
【定理】軸と切片中点
【定理】軸と切片中点
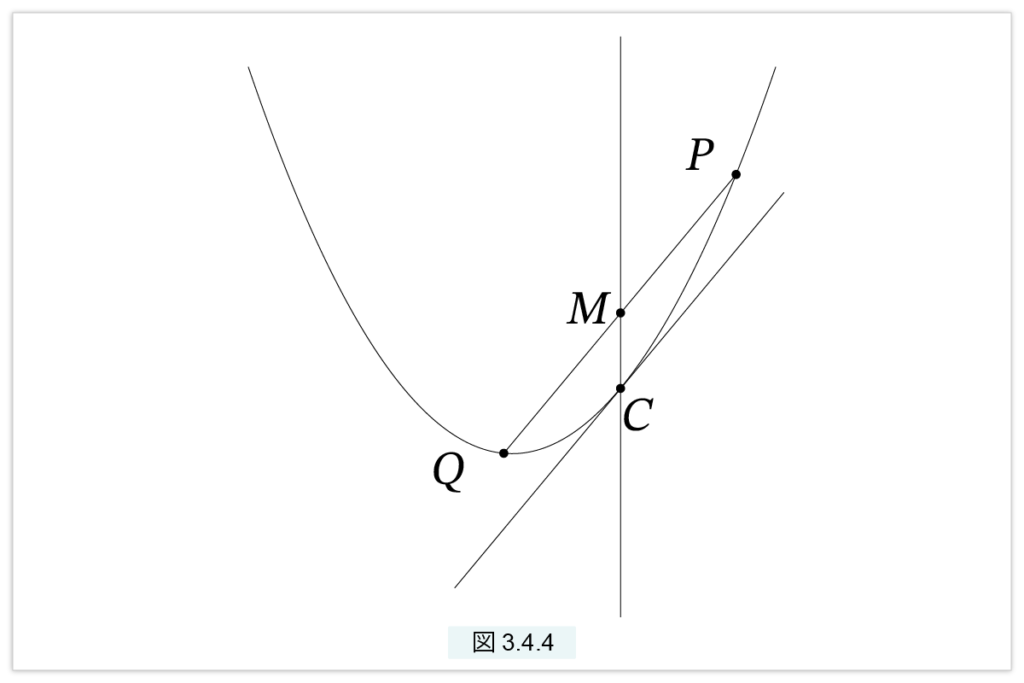
図3.4.4 の放物線で、C を通る接線を斜交軸とする。P と Q を放物線上の点で、PQ は斜交軸に平行とする。すると鉛直軸は PQ の中点を通る。
ー 【定理】軸と切片中点の証明 ー
r を定理〔斜交座標〕を満たす線分とする。MをPQ と鉛直軸の交点とすると次が成立する。
□2(PM) = □(r, CM) = □2(QM)
よって、PM=QM となる。
【定理】斜交座標の接線
【定理】斜交座標の接線
図3.4.5 で CB は斜交軸、P,Q は放物線上の点で CB と並行とする。鉛直軸とPQ との交点を M とし、Pにおける放物線の接線と鉛直軸の交点を R とすると、MC = CR が成立する
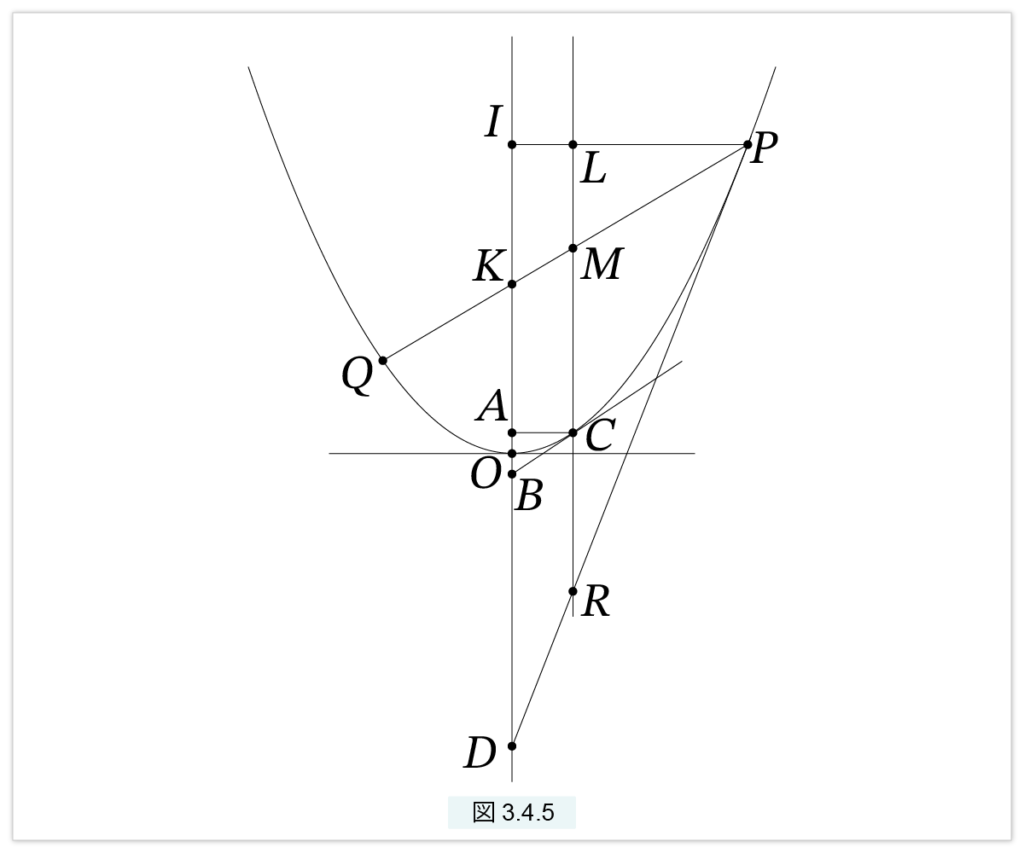
図の説明をしておきます。O は放物線の頂点で、IKAOBD は放物線の中央軸です。CB は放物線の接線で、LMCR は斜交座標の鉛直軸です。ILP と AC は水平です。次のように記号を振ります。
AC=a, AO=b, IP=x, IO=y
ー 【定理】斜交座標の接線の証明 ー
アルキメデスは比を使って証明していますが、比の理論は制約が多く独特の技法を要し、証明の筋がなかなか見えません。そのため本節では現在の数学を使って記述しますが、比の理論独特の技法以外は比の理論に変換できます。この放物線の方程式を
py = x2つまり □(p, y) = □2(x)
とします。C は放物線上の点だから pb = a2 となります。よって
\( y = \frac{x^2}{p} , \quad b = \frac{a^2}{p} \) (4)
が成立します。後でこの式を使って y と b を消去します。CB と PD は接線ですから〔放物線の接線〕定理より、次が成立します。
AB = 2AO = 2b, ID = 2IO = 2y
以下で MC が MR の半分であることを証明します。そのためまず LM の長さを求めます。△CAB, △PIK, △PLM は相似であることと (4) より
LM/LP = IK/IP= AB/AC = 2b/a = 2a2/ap = 2a/p
が成り立ちます。よって、LP = x – a ですから
\( LM = LP \times \frac{LM}{LP} = ( x – a ) \times \frac{2a}{p} \) (5)
となります。次に △PID と △PLR が相似であることと、ID= 2y より
\( LR = ID \times \frac{LP}{IP} = 2y \times \frac{x-a}{x}
= \frac{2x^2}{p} \times \frac{x-a}{x} = \frac{2x}{p}(x-a) \)
となります。これから (5) を引くと
\( MR = LR – LM = \frac{2x}{p}(x-a) – \frac{2a}{p}(x-a) = \frac{2}{p}(x-a)^2 \) (6)
が得られます。次に MC をもとめます。(4) と (5) を使います。
\( LC=IA=IO – AO = y – b = \frac{x^2-a^2}{p} \)
\( MC = LC -LM = \frac{x^2-a^2}{p} – \frac{2a(x-a)}{p} \)
\( = \frac{1}{p}(x^2 -a^2 -2ax + 2a^2) = \frac{1}{p}(x-a)^2 \) (7)
(6) と (7) より MR = 2MC が得られます。
アルキメデスはこれらの定理を使って放物線の切片の面積を求めました。次節でこの計算方法について詳しく解説します。

