小石の数理
アルキメデスの面積と体積
放物線の求積
3-3. アルキメデスの放物線の面積|相似と天秤による古代の求積法
前節では放物線の描き方について解説しました。この節ではアルキメデスが考えた「放物線の切片の面積」について詳しく見てみましょう。アルキメデスの証明には独創的なアイディアによるものが多く、これもその一つなのですが、現在の皆さんは比の理論に慣れていないので、比の理論の復習をしてから述べることにします。
ページ目次
相似な三角形の面積比
【定理】相似な面積比
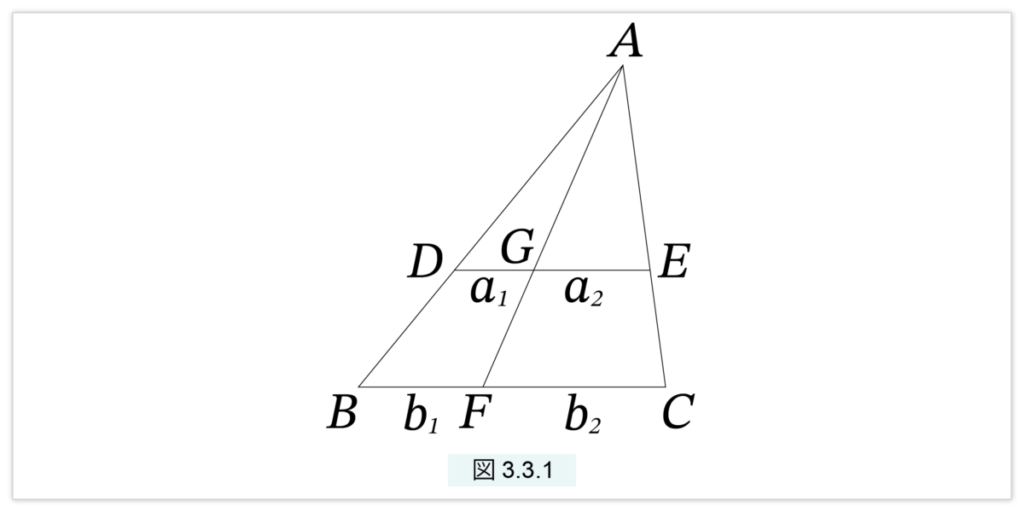
図3.3.1 を見てください。DE と BC は平行とします。△ABC には相似の三角形がたくさん現れ、次が成立します。
a1 : b1 = AG : AF = a2 : b2
内項を交換すると、
a1 : a2 = b1 : b2
が成立します。したがって、特に
a1 = a2 ⇔ b1 = b2
が成立します。
おそらく皆さんは次の定理をご存知だと思います。
【定理】相似な面積比
相似な三角形の面積の比は対応する辺の長さの2乗の比となる
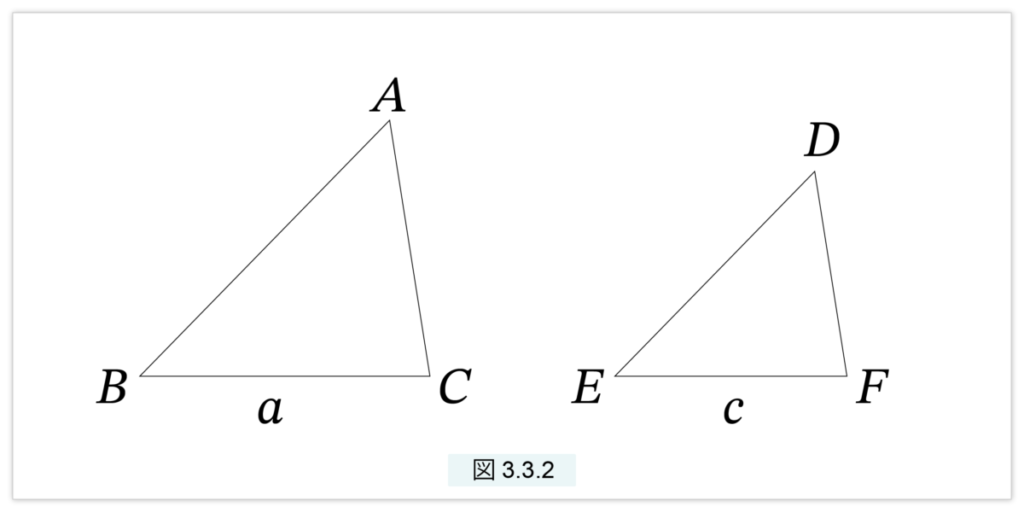
図3.3.2 で、△ABC と △DEF が相似だったとします。BC=a と EF=c が対応する辺です。定理は次が成立すること主張します。
△ABC : △DEF = □2(a) : □2(c)
現在では中学生程度の問題ですが、古代ではこれをどのように証明したか見てみましょう。
相似な面積比 -古代ギリシアの証明方法
△ABC の高さを b、 △DEFの高さを dとします。
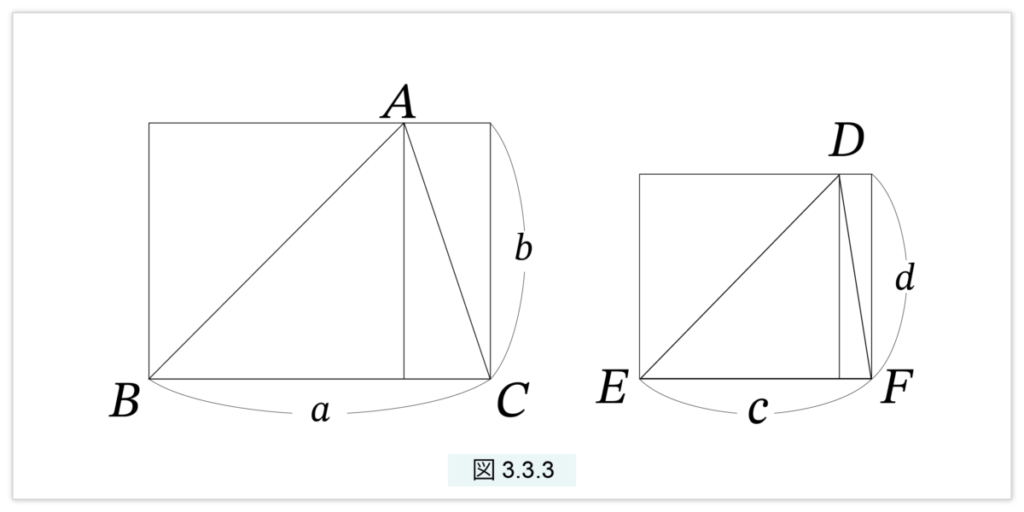
すると図3.3.3 より、
2△ABC = □(a, b),
2△DEF = □(c, d)
が成立します。よって
△ABC : △DEF = □(a, b) : □(c, d) (1)
底辺が同じ長方形の面積は高さに比例しますから、
□2(a) : □(a, b) = a : b,
□2(c) : □(c, d) = c : d,
△ABC と △DEF は相似ですから、
a : b = c : d
よって、
□2(a) : □(a, b) = □2(c) : □(c, d)
が成立します。内項を交換すると、
□2(a) : □2(c) = □(a, b) : □(c, d)
となります。よって (1) より、
△ABC : △DEF = □2(a) : □2(c) (2)
となります。
〔相似な面積比〕の定理 は多角形に拡張できます。相似な多角形は相似な三角形に分割できます。
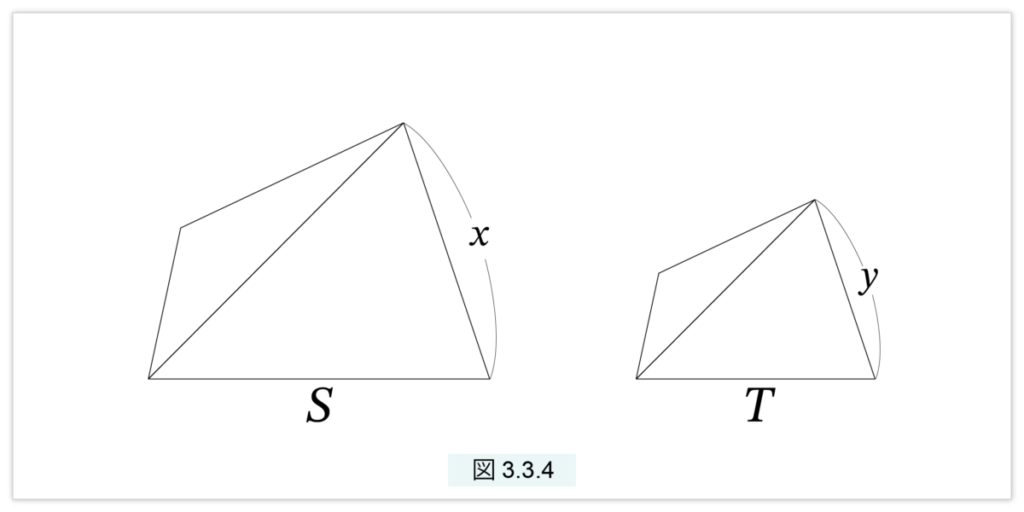
図3.3.4で S と T は相似な多角形、x と y は対応する辺とします。このとき次が成立します。
多角形 S : 多角形 T = □2(x) : □2(y)
【定理】放物線の切片
放物線の切片 の定理
さて、本節の本題は以下の定理です。
【定理】 放物線の切片
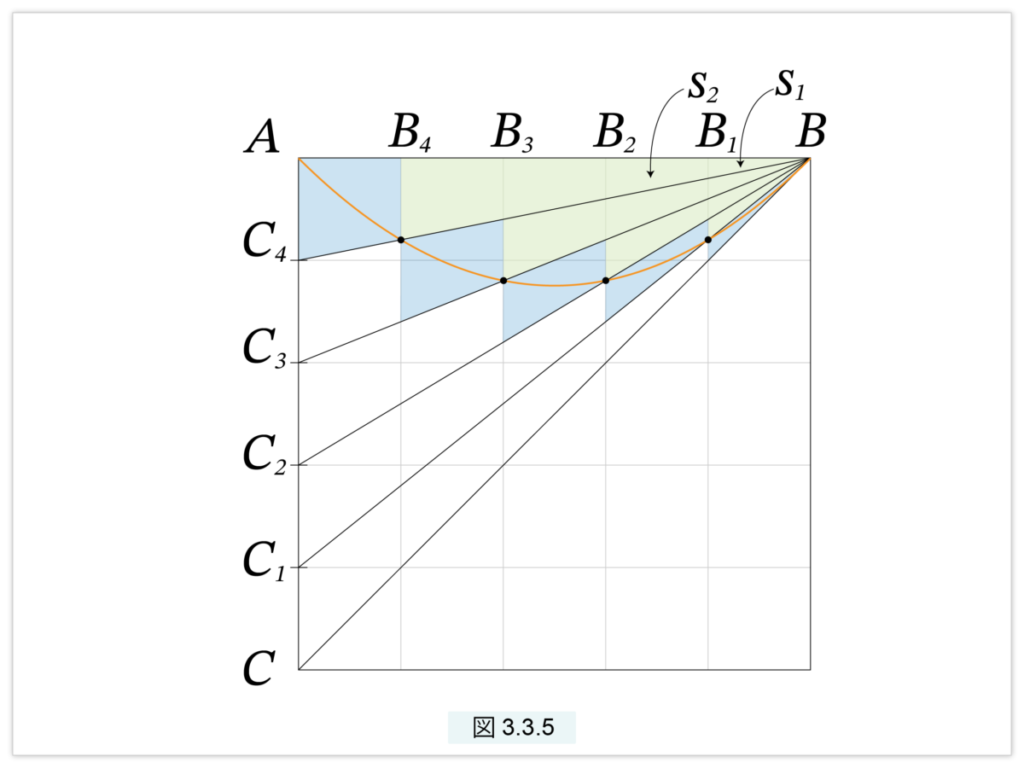
図3.3.5 で次が成立する
切片AB =1/3 △ABC
切片AB とは、放物線と線分 AB で囲まれた部分のことです。この定理を証明しましょう。
放物線の切片の定理 の証明
直角三角形AB を図3.3.5で示されるように小さな図形に分解します。図3.3.5 では AB と AC をそれぞれ5等分していますが、この5 は準一般的な表現で、現在では変数 n を使って表します。現代風にいいなおすと次のようになります。
AB と AC を n 等分し、AB の各点 B1, B2,…, Bn-1 には縦線を引き、CAの各点 C, C1, C2,…, Cn-1 は B と結びます。前節で議論したように、Bi を通る縦線と CiB との交点は放物線上の点となります。これらの線で囲まれた最小の四角形または三角形の一つずつをセルと呼ぶことにします。切片AB を覆う最小のセルの集合を外接図形と呼び Wn で、切片AB に含まれる最大のセルの集合を内接図形と呼び Vn で表すことにします。放物線の上にあるセルの集合を Tn で表します。内接図形 Vn は緑色で、Tn は青色で示されています。 以下では次を示します。
Vn < 切片AB < Wn = Vn + Tn (3)
アルキメデスは実に巧妙な方法で Vn, Wn, Tn の計算をしています。AC を三角形 BAC の底辺と見なすと、底辺は n 等分され、△BAC は n 個の面積が等しい三角形に分割されます。
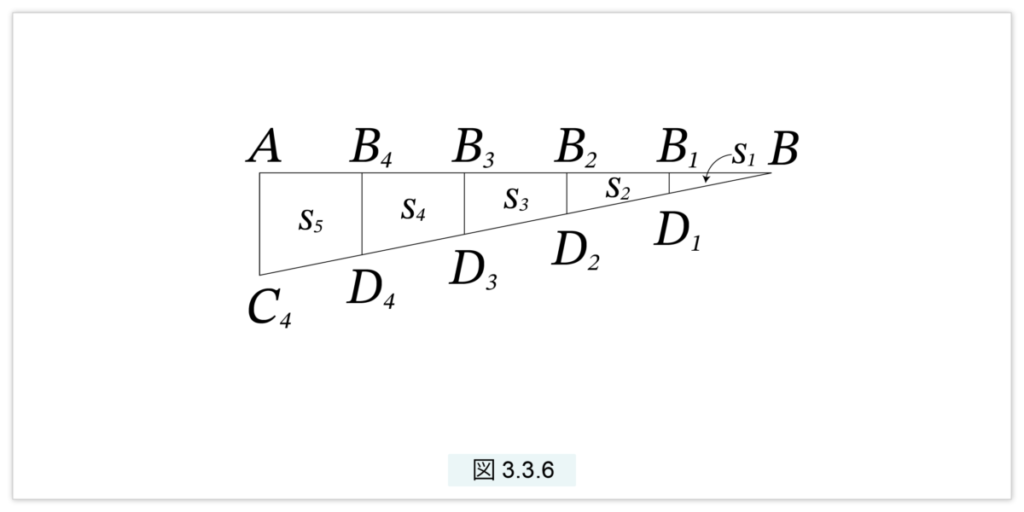
図3.3.6 はそのうちの一番上の三角形です。これらの三角形はn個の等間隔の縦線で分割されます。 縦線はAC と並行なので、上で示したように、各縦線は△ABCの部分を等間隔で分割します。したがって、縦に現れるセルはすべて同じ面積となります。B=B0 と B1 の間に現れるセルを s1、B2 と B2 の間に現れるセルを s2、… と番号を振ります。図3.3.5では、一番右には三角形 s1 が n個、次は台形 s2 がn個、…と縦にはすべてセルがn個並んでいます。図3.3.5 では次のようになっています。
V5 = s4 + 2s3 + 3s2 + 4s1
T5 = s5 + s4 + s3 + s2 + s1
ここで
S = △ABC, s = s1
と置きます。古代では面積は比で表すのですが、以下では現代風に数値として計算します。
図3.3.6 の小三角形 BACn-1 を考えます。△BB1D1 が基本となる三角形 s=s1 です。△BB2D2 は底辺と高さが、基本三角形のそれぞれ2倍だから面積は4倍、△BB3D3 は底辺と高さがそれぞれ3倍だから面積は9倍、… となり一般に次が得られます。
s1 + s2 + … +sn = n2s
となります。したがって、
△BACn-1 = s1 + s2 + … +sn = n2s
一方、△BACn-1 = (1/n)S ですから
\( s =\frac{1}{n^3}S \)
となります。
さて、外接図形 Wn の計算をしましょう。外接図形を C1B, C2B, … で切り分けます。C1B で切り取られるのは、図3.3.5 の右端の一番下に現れる s1 です。次に C2B に切り取られるのはその下の三角形 s1+s2、 … 最後に Cn-1B に切り取られるのは s1+s2+…+sn です。このようにして Wn が計算できます。
Wn = s1 + ( s1 + s2 ) + … + (s1 + s2 + … +sn )
= { 12 + 22 + 32 + … + n2 }s = \( \frac{1}{6} \) n(n+1)(2n+1)s
Vn についても同様に
Vn= { 12 + 22 + 32 + … + (n-1)2 }s = = \( \frac{1}{6}\) n(n-1)(2n-1)s
が得られます。これより次が成立します。
\( V_n < \frac{n^3}{3}s = \frac{1}{3}S < W_n \hspace{40pt}\) (4)
一方 Tn は放物線上のセルの集合ですから、図3.3.5 の影のかけられたセルの集合です。したがって
Tn = s1 + s2 + … + sn
= △BACn-1 = \( \frac{1}{n}\) △ABC = \( \frac{1}{n} S \hspace{40pt} \) (5)
となります。Vn と Wn の差 Tn は、n を大きくとればいくらでも小さくできます。したがって (4)と (5) より
切片AB = \( \frac{1}{3}\)S
が示されました。
放物線の接線の面積 – 天秤による方法 –
アルキメデスの天秤
後にアルキメデスは、天秤を使って驚くべき簡単な方法で放物線の切片の面積を求めています。アルキメデスは、「この方法は正しい結果を導くが(幾何学的に)証明されたわけではない。結論は正しいと考えて証明を与えるべきであろう」と述べています。
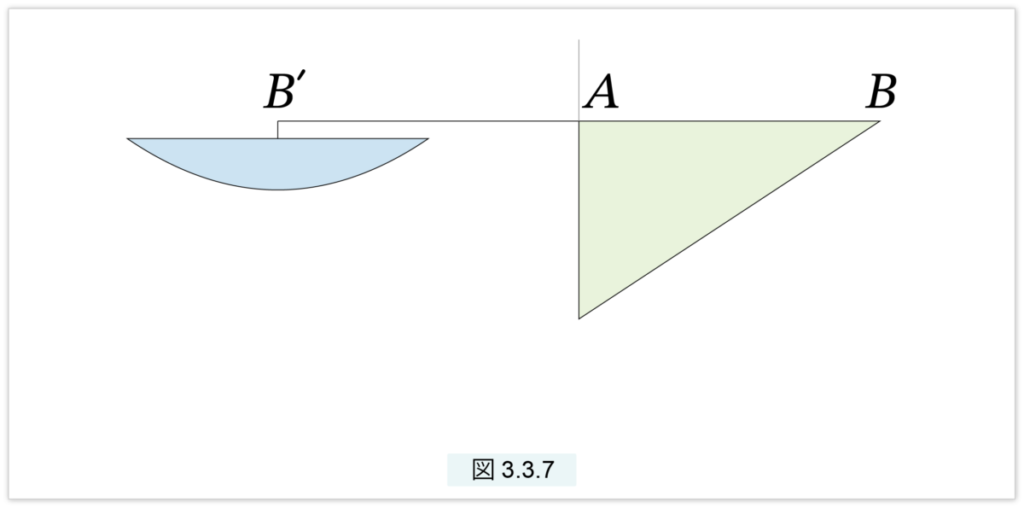
図3.3.7 のように、A を支点とした天秤に、三角形ABC と放物線の切片AB を吊るします。三角形は辺 AB を天秤の棒に付け、切片は真ん中で B’ に吊るします。ここで、AB=AB’ とします。すると、図3.3.7 で示されているように天秤はつり合うのです。この天秤はなぜ釣り合うのでしょうか。
天秤による方法 の証明
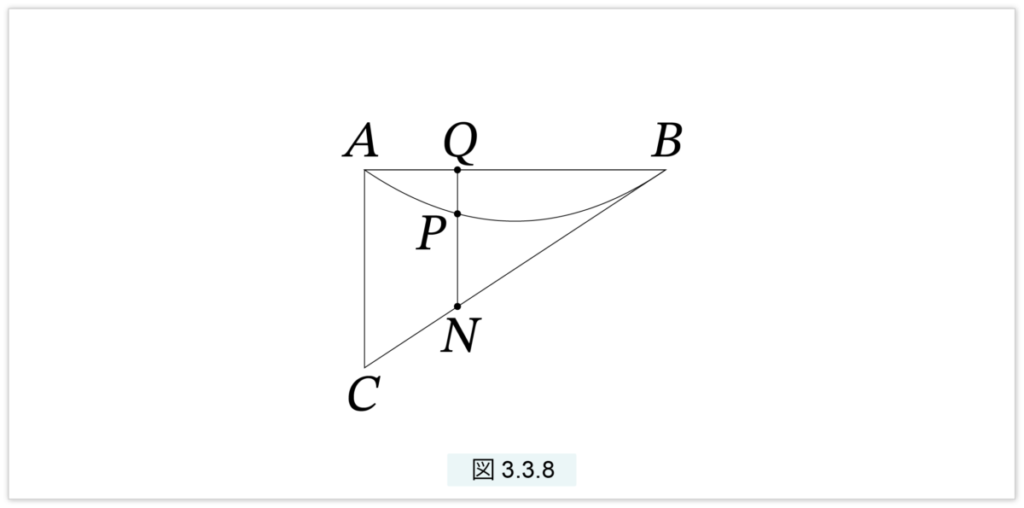
図3.3.8 で、点Q を、AからBまで移動すると、Pは放物線上をAからBまで移動し、棒QP は切片を描きます。同様に点N はC から B まで移動し、棒QN は三角形ACB を描きます。
上で“線”ではなく“棒”といったのは、後世になって、QP とか QN は「幅のない“線”」とみなされるようになり「幅0のものをいくら集めても面にはならないし、重さもいくら集めても0のままだ」という物議を醸すことになるからです。アルキメデスは、そんなことまで考えていなかったと思います。ここでは、棒はごく小さな(たとえば原子の大きさぐらいの)幅をもつとします。
Q がAB 上のある1点にあったとします。前節で述べた 補助定理〔放物線と直角三角形〕より
QP : QN = AQ : AB
が成立します。これは図3.3.9 で示される A を支点とする天秤に、Qのところに棒 QN を、B’ のところに棒 QP をつるすと釣り合うことを意味します。
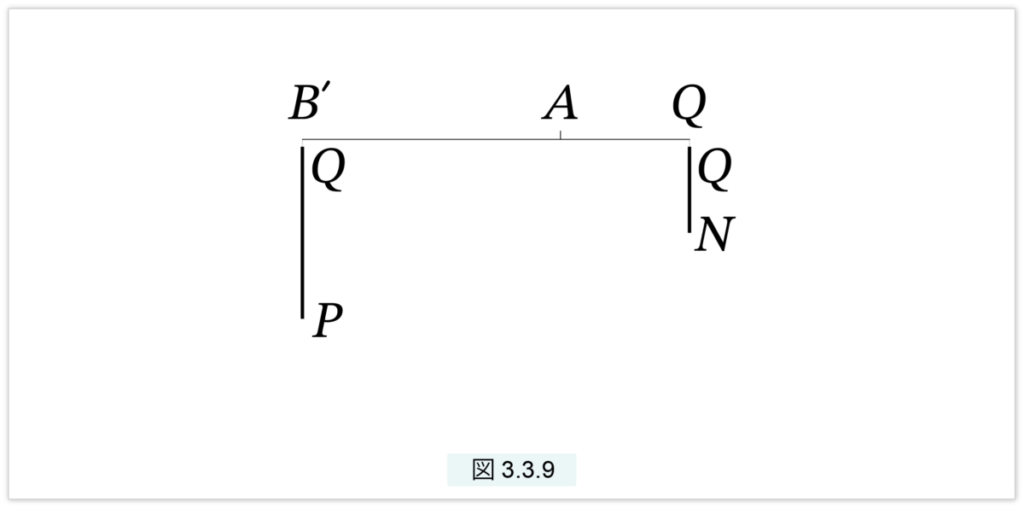
QがAからB まで動くと、天秤の右側には直角三角形 ACB がぶら下がり、天秤の左の B’ には放物線の切片が全て集められて、最終的に切片AB となります。天秤の右側の三角形を1点で吊るすには、図3.3.10 が示すように、AB を 1 : 2 に分ける点でつるすと、天秤はつり合います。
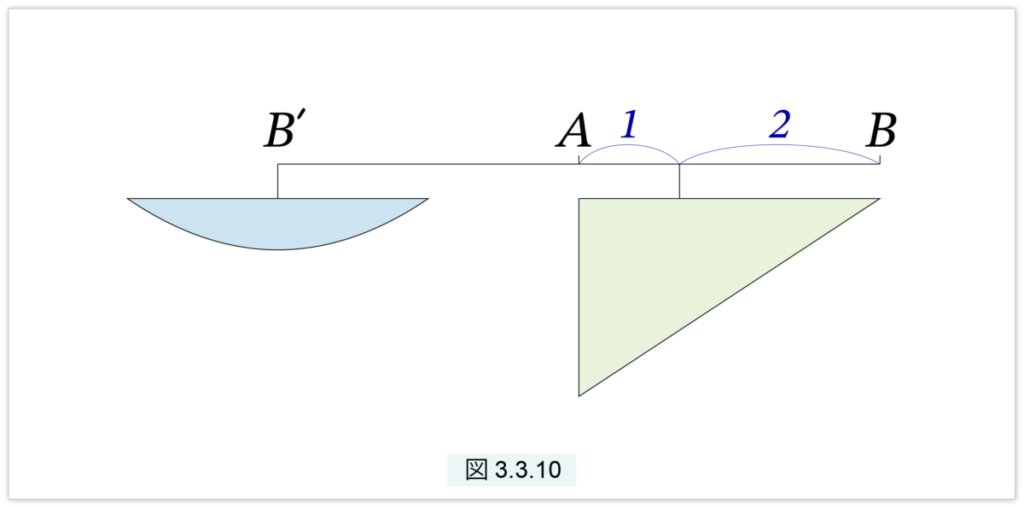
図3.3.10 より、次が成り立つことが分かります。
切片AB = \( \frac{1}{3}\)△ABC

