小石の数理
アルキメデスの面積と体積
放物線の求積
3-2. 放物線の描き方 | アルキメデスが考えた方法を詳しく解説
アルキメデスは放物線に対するいろいろな性質を知っていて、その性質を使ってさまざまな結果を得ています。放物線の描き方についても示しています。古代ギリシアの時代のアルキメデスが放物線をどのように考えたのか、詳しく見てみましょう。
ページ目次
放物線とはどのような曲線か
古代における放物線の表し方(前節の復習)
前節〔3-1. 放物線とは〕で述べたように、アルキメデスは放物線を、次を満たす2つの線分 x と y によって定められる点が描く曲線として捉えました。
□(p, y) = □2(x) (1)
ここで p は固定された線分、x と y は長さが変化する線分です。
線分 p が与えられたとします。点 O を通る直線を引き、この直線上に点 H を、OH=p となるように取り、H を通る垂線を引きます。点 H は、O の右側に取るときと、左側にとる場合があります。今回は右側にとった場合を考えます。線分 OH 上( 図3.2.1(a) )か、OHの延長線上( 図3.2.1(b) )に点 A をとり、OA=x と置きます。
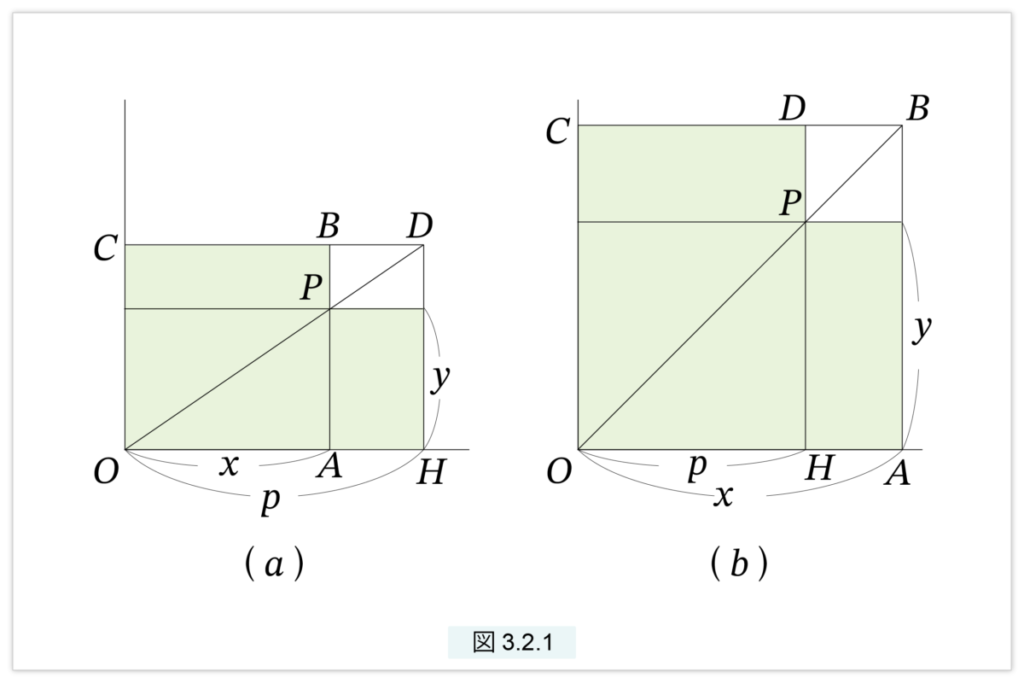
図のように正方形 OABC を描きます。H を通る OA の垂線を描き直線 CB との交点を D とします。直線 OD と 直線 AB との交点を P とします。PA が求める線分 y で、OA が x です。これで O の右側の放物線が描けました。点H を O の左側にとれば、同様にして O の左側の放物線が描けます。
このようにして描かれる点 P の軌跡が放物線で、点 O を放物線の頂点、直線 CO を中心軸、OA を水平軸と呼びます。
図3.2.1(a), (b) の影で示されたL字型の図形は〔2-6 グノモンの定理〕で述べたグノモンです。グノモンの定理 より、p, y, x は (1) を満たします。
アルキメデスが考えた放物線
アルキメデスは、曲線を2つの基準となる直線をもちいて定めました。ここではこれを中心軸、水平軸と呼びましたが、実際には向きは決まっていません。水平軸は、水平でなくても、垂直でも斜めに傾いていてもかまいません。また、2つの基準となる直線は直交しなくてもかまいません(直交していない座標系を斜交座標といいます)。アルキメデスには“座標”という概念はありません。式 (1) で x, y, p は、それぞれ線分(の長さ)です。古代では、単に“線分”といった場合、線分自身を表す場合と、その長さを表す場合とがあります(三角形や四角形とその面積についても同様です)。しかし座標は便利なので、説明のために本連載では座標は使うこととします。
復習しますと、放物線とは式 (1) が満たす点 P が描く曲線です。ここで p は固定された線分、y は P から中心軸までの距離、x は P から水平軸までの距離です。(少し紛らわしいですが大文字の P と小文字の p とは何の関係もありません。)
ギリシア数学における制約とは
前節では放物線を現在の数学の概念を使って述べましたが、古代ではこれらの概念を使えません。ここで、古代ギリシアの数学について復習しておきましょう。一番注意すべきことは、ギリシアでは「“数”とは自然数のこと」で、長さとか面積などは“量”として、数とは別ものとして扱っていました。“量”にもいろいろなものがあり、同じ種類の量同士でしか足し算や引き算はできません。たとえば長さと面積は足せません。同じ種類の量は足せますから「自然数×量」は許されます。非常に厳しい制約ですが、アルキメデスはこの制約の下ですばらしい数学を作り上げました。以下で、a, b, c は線分、□(a,b) は a と b を縦と横とする長方形、□2(a) は a を1辺とする正方形とします。このとき次が成立します。
□(a+b,c) = □(a,c)+□(b,c)
□(a – b,c) = □(a,c) – □(b,c), a>b
2□(a, b) = □(2a, b) = □(a, 2b)
a : b = □(a, c) : □(b, c)
a : b = c : d ⇔ □(a, d)=□(b, c) … 内項外項の定理
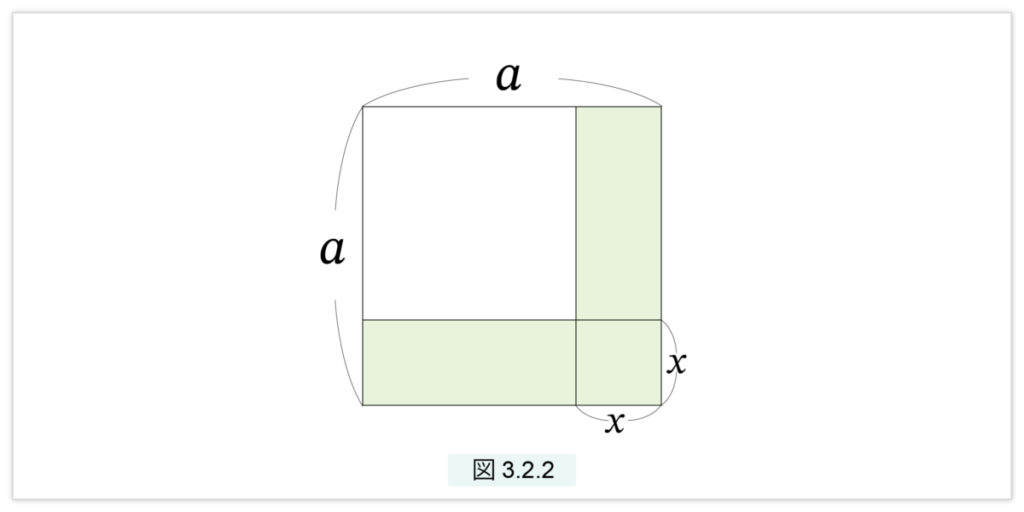
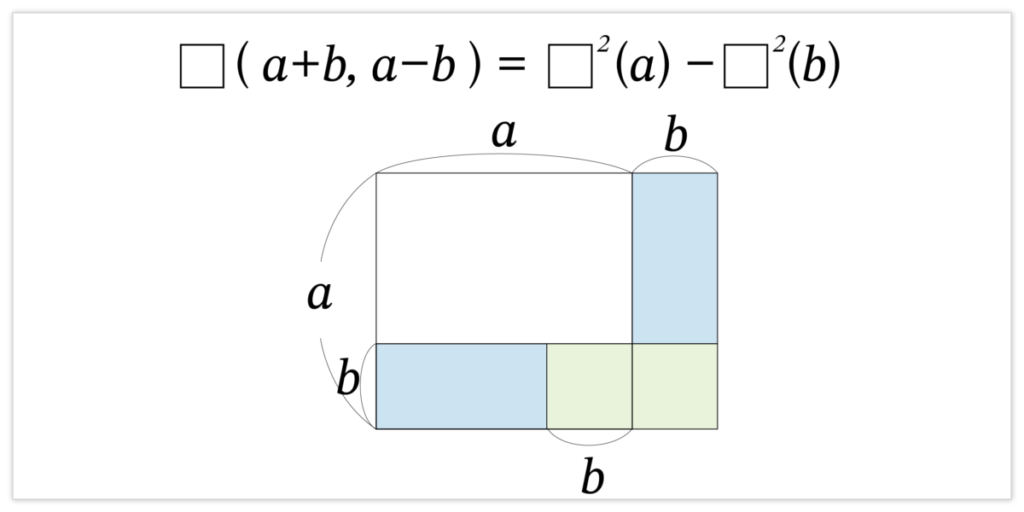
さらに図3.2.2 が示すように、線分 a, x (a>x) に対して次が成立します。
□2(a) – 2□(a, x)+□2(x) = □2(a – x)
放物線の接線
放物線の接線 の定理
放物線の理論で重要な働きをするのは接線です。アルキメデスの時代にもう接線の概念が存在していたとは驚きです。放物線と直線がただ一つの点 P で交わるとき、直線を接線、Pを接点といいます。接線は、円、楕円、双曲線に対しても同様に定義されます。
放物線の接線に関しては次が成立します。
【定理】放物線の接線
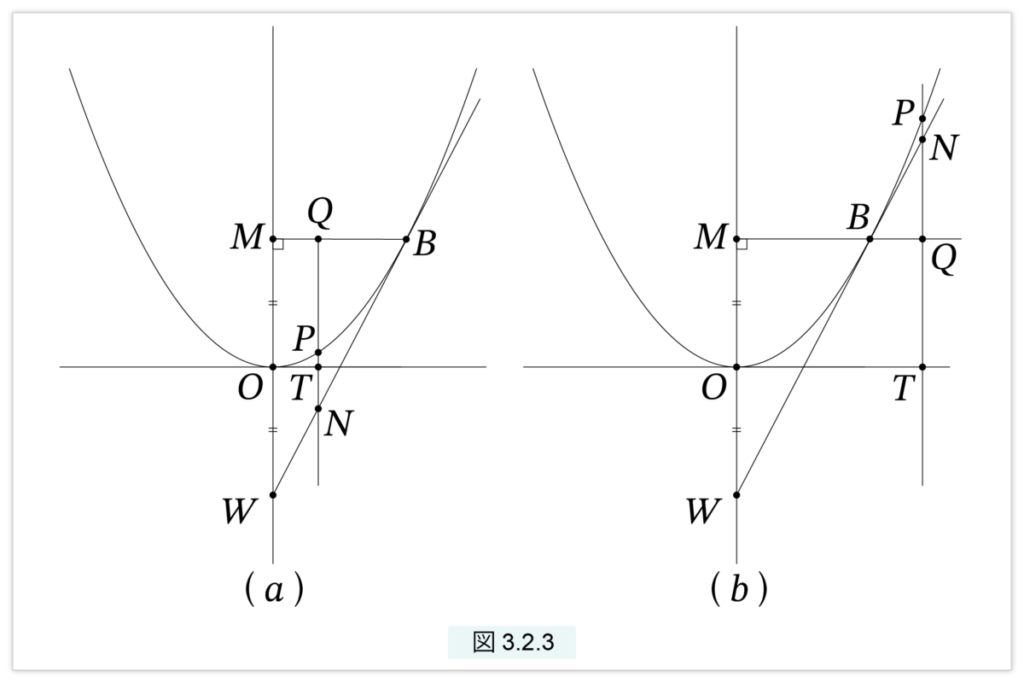
図3.2.3 (a), (b)で、Oは放物線の頂点、B は放物線上の点、BM は中心軸に下ろした垂線とする。中心軸上に点 W をMO=OW となるようにとると、BW は放物線の接線となる。
放物線の接線 の定理 の証明
放物線を □(p, y)=□2(x) とします。p は定められた線分ですが、図には現れていません。点Q をMBまたはMBの延長上に任意に取ります。Qを通る中心軸に平行な直線を引き、この直線と、放物線、水平軸、直線 BW との交点をそれぞれ P, T, N とします。BW が接線であることを示すには、接点を除くすべての BW 上の点が放物線の外側にあることを示せばよいことになります。したがって、点 Q が MB 上にある場合(図3.2.3 (a))は QN > QP が成立し、Q が B の右側にある場合(図3.2.3 (b))は QP > QN が成立することを示します。
MB=a, MO=b, OT=x, PT=y
と置きます。現代的に座標でいえば、B(a, b), P(x, y) と置きます。B と P は放物線上の点だから次が成立します。
□(p, b)=□2(a), □(p, y)=□2(x)
まず Q が MB 上にある場合を考えます。QP を計算したいのですが、割り算が使えないので、代わりに □(p, QP) を求めます。
□(p, QP) = □(p, QT – PT) = □(p, QT) – □(p, PT)
= □(p, b) – □(p, y) = □2(a) – □2(x) (2)
また、△BQN と △BMW が相似であることから
QN : QB = MW : MB = 2b : a = □(p, 2b) : □(p, a)
= 2□2(a) : □(p, a) = 2□(a, a) : □(p, a)= 2a : p
が成立します。この式の最初と最後に〔内項外項〕の定理を適用すると、
□(p, QN) = □(2a, QB)
= 2□(a, a – x) = 2□2(a) – 2□(a, x) (3)
が得られます。式(3) から式(2) を引くと、
□(p, QN) – □(p, QP) = □2(a) – 2□(a, x) + □2(x)
となります。すると、図3.2.2 より
= □2(a – x) > 0
が得られます。したがって、
□(p, QN) > □(p, QP)
が得られ、QN > QP が得られます。
Q が B の右側にある図3.2.3 (b) の場合も、同様にして
QP > QN
が証明できます。証明は割愛しますので、興味のある方はチャレンジしてみてください。
放物線の比による性質
アルキメデスはどのように放物線を描いたか
アルキメデスは次のようにすると放物線が描けることを示しました。図3.2.4 のように長方形を描きます。
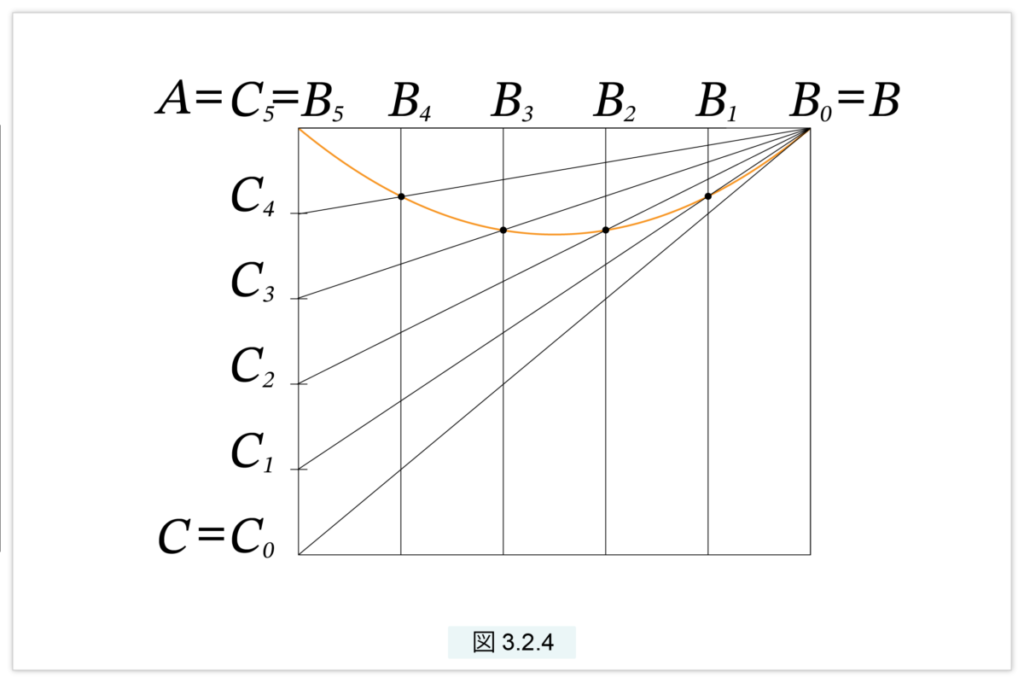
AB と AC を n等分し、AB は右から左へ、 AC は下から上に
B0=B, B1, B1, …, Bn=A,
C0=C, C1, C1, …, Cn=A,
とラベルを振ります。各i(i=1,2,…, n–1)に対し、Bi を通る垂線を引き、Ci と B とを結びます。すると、Bi を通る垂線とBCi との交点が放物線を描きます。以下でこれを証明しましょう。
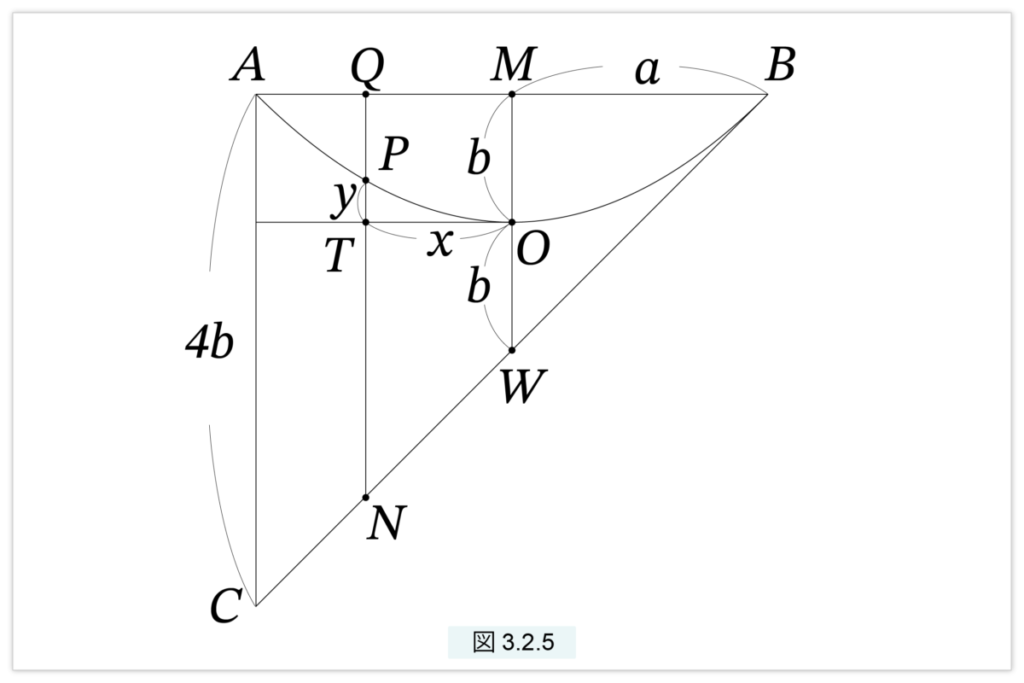
図3.2.5 の放物線 □(p,y)=□2(x) を考えます。A, B を放物線上の点で、AB を軸に垂直とします。O を頂点とし、MOを中心軸とします。したがってMはAB の中点です。MB=a, MO=b と置きます。MO の延長線上に点 W を OW=b となるように取ります。すると〔放物線の接線〕の定理より、BWは放物線の接線となります。A を通る垂線と直線 BW との交点を C とします。すると AC=4b となります。Q をAB上の任意の点とし、Q を通る垂線を引き、点 P, T, N を図のように取ります。Pは放物線上の点、TOはABに平行とします。
TO=x, PT=y
とおきます。
補助定理 1 – 放物線の比による性質
補助定理 1〔放物線の比による性質〕
図3.2.5 において、Pが放物線上の点なら次が成立する
QP : QN = AQ : AB (4)
これは次のように言い換えられる。
□(QP, AB) = □(QN, AQ)
補助定理1 の証明 〈現代数学を使った方法〉
アルキメデスの著作は、主定理を証明するまでに補助定理が続きます。補助定理がどのような役目をするのか、補助定理は何を意味するのか、分からないで読み続けるのはつらいものです。アルキメデスの証明の前に現代数学を使って説明しましょう。原点を頂点とする放物線は、現代では
py = x2 , ただし、pb = a2
と表します。この式を、A を原点とする表現に変換します。AQ=u, QP=v とおくと、
x = u – a, y = b – v
となります。現代の方程式で議論していますから、u<a のときは x はマイナスとなります。これを py = x2 に代入すると
p(b-v) = (u-a)2
となります。pb=a2 を使って変形すると
pb – pv = u2 -2au +a2
a2 – pv = u(u – 2a) +a2
pv = u(2a-u) (5)
となります。式 (5) は、(v を y, u をxと見れば、)原点(0,0) と (2a, 0) を通る放物線を表しています。さらに QN:QB=2b:a, QB= 2a – u を使って (5) を変形すると、
\( u(2a-u) = AQ \cdot QB, \hspace{40pt} \) (ア)
\( pb = a^2\) より
\( pv = \frac{a^2}{b}v = \frac{QB}{QN} \cdot 2av = \frac{QB \cdot AB \cdot QP}{QN} \hspace{40pt} \) (イ)
(ア) = (イ) ですから
AQ・QN = AB・QP
が得られます。言い換えると、(4) の比例式は、現代の放物線を表す式 (5) なのです。
補助定理1 の証明 〈アルキメデスの証明〉
まず □(p, b) = □2(a) に〔内項外項〕の定理 を適用すると
p : a = a : b (6)
が成立します。三角形の相似関係 QN : QB = AC : AB を記号に書き換えると
QN : x+a = 4b : 2a = 2b : a
となり、これに〔内項外項〕の定理を適用すると、
□(QN, a) = □(x+a, 2b) = 2□(x+a, b) (7)
となります。欲しいのは □(QN, a) ではなく □(QN, p) なので、次の比を考えます。
□(QN, p) : □(QN, a) = p : a
(6) を使って等式を続けると
= a : b
= 2□(x+a, a) : 2□(x+a, b)
最後の等式は〔底辺が等しい〕ことから得られます。よって (7) より
□(QN, p) : □(QN, a) = 2□(x+a, a) : □(QN, a)
が得られました。すると、〔右項一致〕の定理 より、
□(QN, p) = 2□(x+a, a) (8)
が得られました。一方、
□(QP, p) = □(QT – PT, p)
= □(b – y, p) = □(b, p) – □(y, p)
= □2(a) – □2(x) = □(a+x, a – x)
となります(最後の行は以下の図を参照)。
よって、(8)より
QP : QN = □(QP,p) : □(QN,p) = □(a+x, a – x) : □(a+x, 2a)
= a – x : 2a = AQ : AB
が得られました。
放物線の描き方
補助定理2
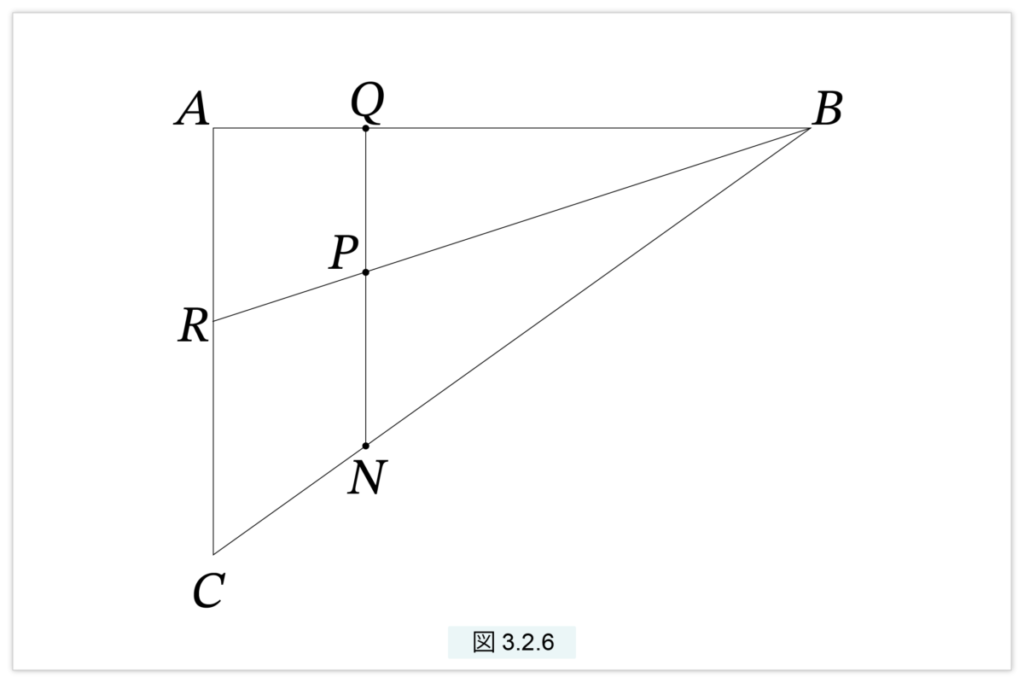
図3.2.6 でABC は直角三角形、Q はAB上の点、R はAC 上の点、QNはACに平行、P はBRと QNの交点です。
〔 補助定理 2 放物線と直角三角形〕
図3.2.6 において次が成立する。
QP : QN = AR : AC (9)
補助定理2 の証明
△BQP と △BAR は相似、△BQN と △BAC は相似ですから、
QP : AR = QB : AB = QN : AC
が得られます。QP : AR = QN : AC に内項の交換規則を提供すると結果が得られます。
放物線の描き方 の定理
補助定理1 の式 (4) と補助定理2 の式 (9) を合わせると次の定理が得られます。
【定理】放物線の描き方
図3.2.6 において、次が成立する。
P は放物線上の点 ⇔ AQ : AB = AR : AC
放物線の描き方 の定理 の証明
放物線上の点 P が上の比例式を満たすことは、2つの補題から明らかです。逆を示しましょう。点 P が AQ : AB = AR : AC を満たしたとしましょう。このとき R を固定し、Q を A から B に向かって移動します。線分 BR 上の任意の点 P に対し QP/QN の値は一定です。一方 AQ/AB の値は Q が右に移動すれば増加します。したがって (9) を満たす P は放物線上の点以外には存在しません。
先に述べた 図3.2.4 に戻りましょう( 図3.2.4 再掲▼)

Q を B1,…, Bn-1 のなかのどれか、R を C1,…, Cn-1 のなかのどれかとすると、
ABi : AB = n – i : n = ACi : AC
となります。したがって、Bi を通る縦線と BCi の交点は放物線上の点となります。

