3-1. 放物線とは？放物線の方程式と接線 | 古代の放物線の表し方

「高校で習う数学など私たちの毎日の生活には何のかかわりもない」というような話をよく聞きます。特に二次方程式とか 放物線 などは、日常生活にはあまり現れません。2千年も前にアルキメデスは放物線、楕円、双曲線などといったとても抽象的な対象を扱っていました。数学は一人でできるものではありません。自分のなしとげたことを理解し評価してくれる集団がいたはずです。実際、アルキメデスは自分の研究した結果をエジプトのアレクサンドリアの図書館長であるエラトステネスに送っています。どんな理論でも、実用的で実践的な問題が動機となって発展してきたと思います。特に放物線、楕円、双曲線といった抽象的な理論は、その理論に至るまでの長い歴史があったに違いありません。アルキメデスの時代には、すでに放物線の理論を、前置きや説明ぬきで受容する環境ができ上っていたようです。

現代における放物線の扱い

放物線の方程式

アルキメデスは2千年も前の人です。アルキメデスの時代から現代にいたるまでの間に、数学はだいぶ進歩しました。数学がどのように進歩してきたかを見るには、現在の数学の概念を使うのはよくないと数学史の専門家はいいますが、これがなかなか難しいのです。本説では、放物線についてアルキメデスの時代と現代の違いについて述べてみたいと思います。

現代では放物線は方程式

y ＝ ax²                                                               (1)

で表し、図3.1.1 のような xy座標で図示されます。

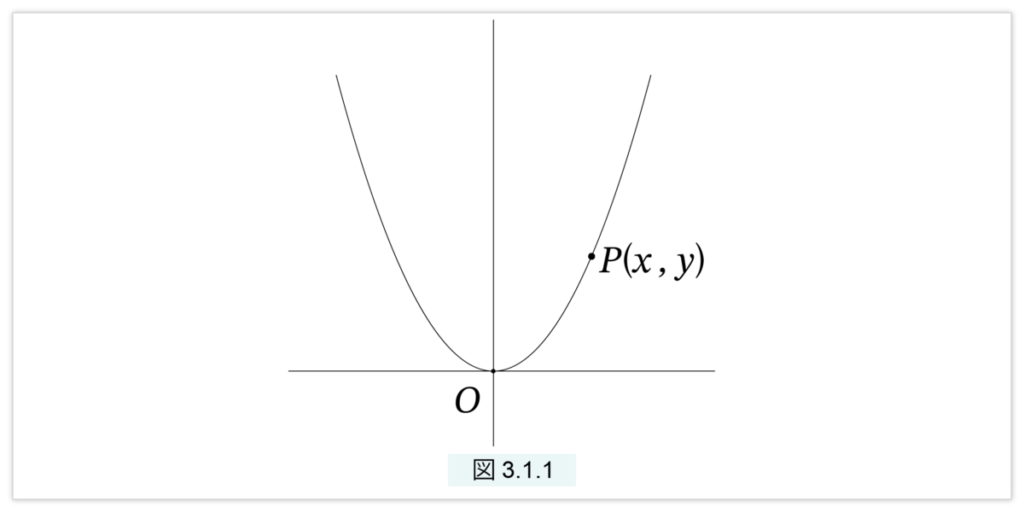
放物線上の点 P は、(1) を満たす2つの実数 x と y の組 (x, y) で示されます。組 (x, y) を点 P の座標といい、点 P(x,y) と引用されることがあります。現代数学では、形式的に「放物線とは (1) を満たす組 (x, y) 全体からなる集合のことである」と定義されます。点Oを放物線の頂点、y軸を放物線の中心軸と呼びます。放物線とただの1点で交わる直線をP を接点とする接線といいます（図3.1.2 ）。

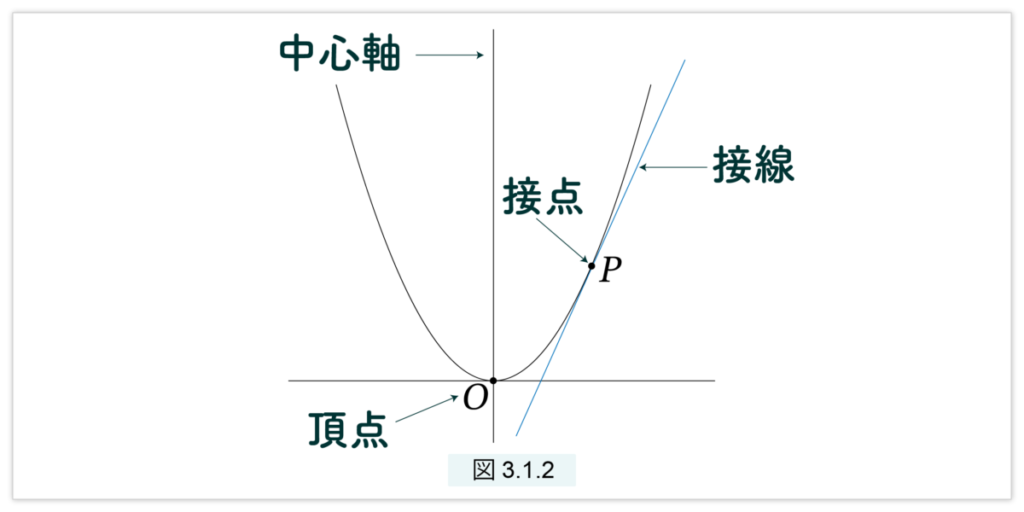
本節では放物線の接線に関する2つの定理を紹介し、現代の方法で証明します。古代の証明に関しては次節以降で解説します。

放物線の接線

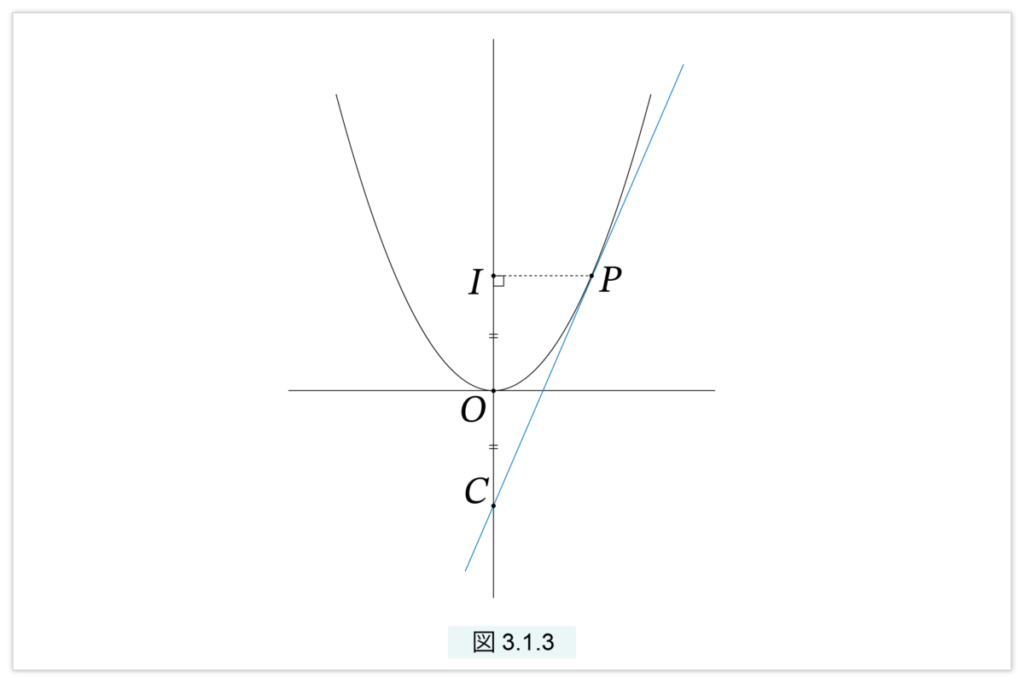
【定理】放物線の接線 の証明

Q を放物線上の任意の点、QJ を軸に下ろした垂線とします。直線 JQ と直線 CP との交点を R とします。（図3.1.4 ）

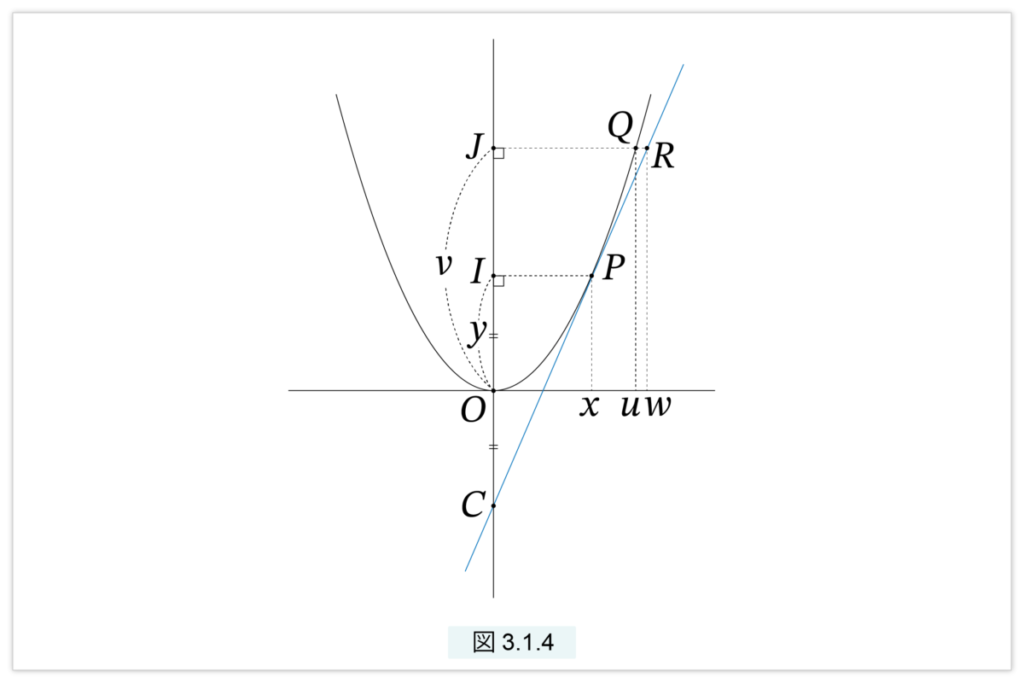
CP が放物線の接線であることを示すには、任意の Q に対し、

\( RJ \geqq QJ  \hspace{60pt} \) (2)

が成り立つこと、さらに等号が成り立つのはQ が P に一致するときに限ることを示します。P, Q, R の座標を次のように定めます。

\( P(x, y), \hspace{6pt} Q(u, v), \hspace{6pt} R(w, v) \)

すると、(2) は次のように表されます。

\( w ≧ u   \hspace{60pt} \) (3)

P と Q は放物線上の点なので、

\( y ＝ ax^2,  \hspace{10pt} v ＝ au^2 \hspace{60pt} \)   (4)

よって、

\(u^2= \frac{v}{a} , \hspace{10pt} x^2 = \frac{y}{a} \hspace{60pt} \) (5)

となります。IP＝x, IR＝w, IC＝2y, JC＝v＋y なので、直線 CPR の傾きは

\( \frac{2y}{x} = \frac{v+y}{w} \)

となります。これを次のように変形します。

\( w = \frac{(v+y)x}{2y} \)

2乗して、x² に (5) を代入します。

\( w^2 = \frac{(v+y)^2 x^2}{4y^2} = \frac{(v+y)^2}{4ay} \hspace{60pt} \) (6)

(6) から (5) を引くと、

\( w^2 – u^2 = \frac{(v+y)^2}{4ay} – \frac{v}{a} =\frac{(v-y)^2 }{4ay} \geq 0\)

上式が 0 となるのは v＝y のとき、つまり Q がPに一致するとき、またそのときに限ります。

放物線の切片と接線

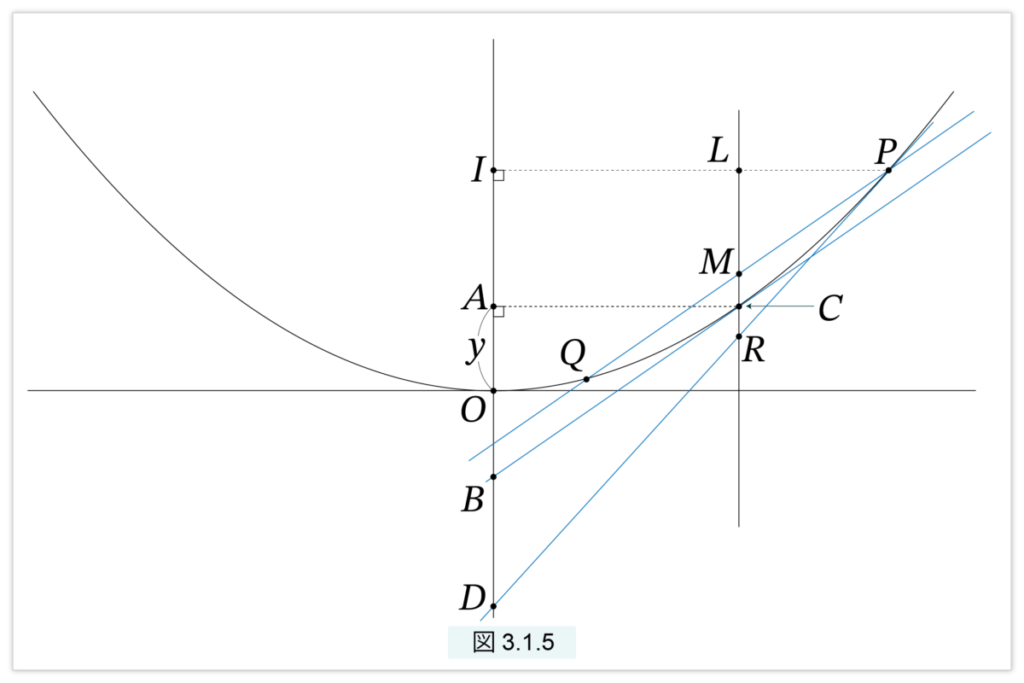
【定理】放物線の切片と接線　の証明

CAを軸に下ろした垂線とすると、(1) 定理〔放物線の接線〕より、AB ＝ 2y だから、

CBの傾き \( = \frac{2y}{x} = \frac{2ax^2}{x} = 2ax\)
PQの傾き \( = \frac{y_1 – y_2}{x_1 – x_2} = \frac{ax_1^2 -ax_2^2}{x_1-x_2} = 2a(x_1 + x_2) \)

CB と PQ は平行だから、これらの傾きは等しい。

\( 2ax = a(x_1 + x_2) \) よって、　\( x = \frac{x_1+x_2}{2} \)

P と Q の中点 M の座標は \( \left( \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2} \right) \)です。よって C を通り、軸に平行な直線は M を通ります。次に (2) を示します。まず、(1) より

\( x = \frac{x_1+x_2}{2} \)

定理〔放物線の接線〕より、ID ＝ 2y₁ だから、

接線 DP の傾き \( \frac{ID}{IP} = \frac{2y_1}{x_1} = 2ax_1\)

IPとMRの交点をLとすると

\( LC = IA = IO -AO = y_1 – y = ax_1^2 – ax^2 = a \left\{ x_1^2 -\left( \frac{x_1 + x_2}{2} \right)^2 \right\} \)

(PM の傾き)＝(BC の傾き) ＝ 2ax だから

\( LM = LP \times (PMの傾き) = \frac{x_1-x_2}{2} \times 2ax = \frac{(x_1-x_2)(x_1+x_2)}{2}a \)
\( MC = LC – LM = a \left\{ x_1^2 -\left( \frac{x_1 + x_2}{2} \right)^2 – \frac{(x_1-x_2)(x_1+x_2)}{2} \right\} = a \frac{x_1^2 -2x_1x_2+x_2^2}{4} = a \frac{(x_1-x_2)^2}{4} \)

次に LR, MR を計算します。M はPQ の中点ですから LP ＝ (x₁ – x₂)/2、よって、

\( LR = LP \times (DPの傾き) = \frac{x_1 – x_2}{2} \times 2ax_1 \)
\( MR = LR – LM = \frac{x_1-x_2}{2} \times 2ax_1 – \frac{(x_1-x_2)(x_1+ x_2)}{2}a = a \frac{x_1-x_2}{2} \left\{ 2x_1 – (x_1 + x_2 ) \right\} = a \frac{(x_1-x_2)^2}{2} \)

よって、MC は MR の半分です。

今回紹介したように、現在の方法は計算はたいへんですが、やり方さえ覚えてしまえば、いつも同じ方法でできます。アルキメデスの時代ではどのように証明していたのでしょうか。古代における証明方法は〔3.4 斜交座標〕で述べます。

古代における放物線の扱い

古代では放物線をどのように表したか

上で述べたように、現在の私たちは放物線を方程式 y ＝ ax² で表します。ここで a は実定数、x と y は実数上の変数です。古代ギリシアではこのような式は使えませんが、もっと重要なことは掛け算がないということです。上の方程式は古代では、

□(p, y) ＝ □²(x)                                                      (7)

と表しました。ここで p は与えられた線分で、x と y は（長さが変化する）線分です。p は固定されていますが、(7) を満たす辺 x, y はいろいろあり、したがって、底辺が x、高さが y の長方形 □(x,y) も変化します。たとえば 図3.1.6 のように、□(x, y) の底辺を水平に置き、底辺の一つの頂点を O に固定すると、O の対角線上にある頂点が放物線を描きます。

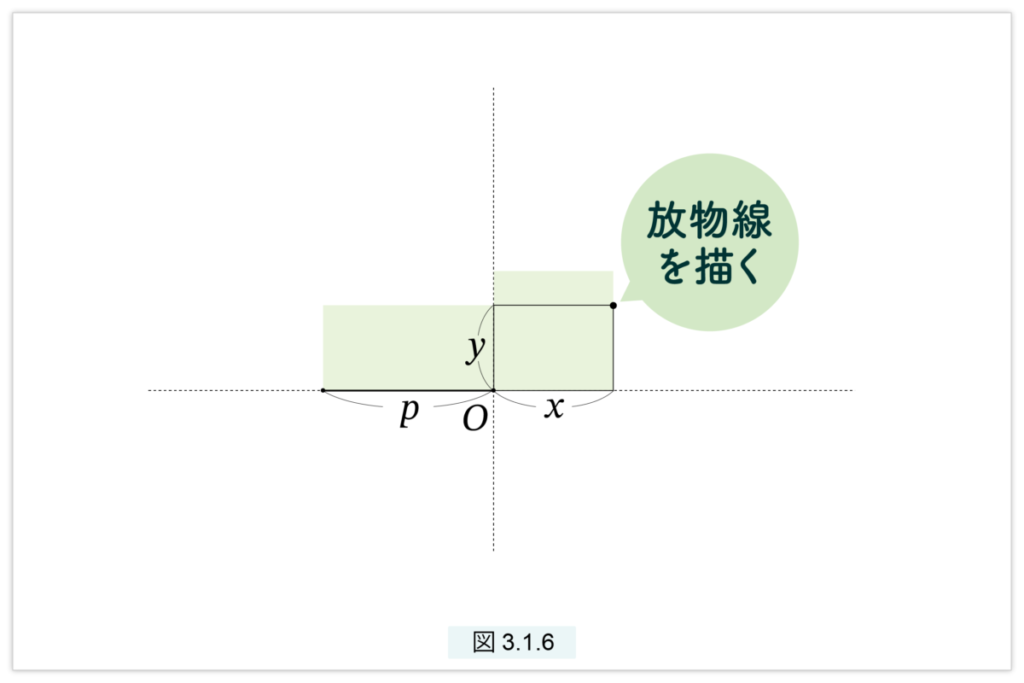
長さや面積は掛け算ができなかった

上では説明のため、□(x, y) の底辺 x を水平に置きましたが、古代では放物線はどちらを向いていてもかまいません。 現在では、放物線上の点は座標として扱われます。したがって、頂点がどこにあるかによって違った方程式となります。また、放物線が横向きであったり、頂点が上にあったりすると違った方程式となります。古代では、座標とか線分の長さを数値で表すことはありませんでした。したがって、放物線を現代のように y ＝ ax² 表し、ギリシア時代のように解釈すると、ax² は「縦x、横x、高さa の直方体(の体積)」を表すことになってしまいます。重要なことは、長さとか面積などの量に関しては掛け算や割り算が許されていない、ということです。次節では、(7) で定義される放物線がどのように描かれるかを見てみましょう。