2-8 量の列の和 〜円錐の体積〜

現在の私たちはすべての物を数値化して考えます。したがって古代ギリシアでも当然同じだったに違いないと思いがちです。しかし、これまで見てきたように、古代ギリシアでは、長さ、面積、体積、…といったものは“数”とみなしていなかったのです。数学において、数列が重要な役割をします。1章で見たように、自然数の数列については重要な成果を得ていました。量に関しても、量の列や、量の列の和を扱っていますが、そこで用いられるのは比の理論であり、“幾何学的な手法”です。この説では「円錐の体積は同じ底面、同じ高さの円柱の 1/3 である」ことを証明します。

体積の求め方 ：「量の列の和」を考える

四角錐（ピラミッド）の体積の復習

円錐の体積は同じ底面、同じ高さの円柱の 1/3 である

この定理は『原論』※の第XII巻にあります。〔1-4 ピラミッドの体積〕では、四角錐の体積を求めました。そこで用いたのは 小石の数理（整数論）です。小さい直方体のブロックを積み、ピラミッドを作って、ブロックの個数を数えました。しかし、円錐の場合は直方体のブロックを積むわけにはいきません。底円の半径が順次増加する円柱を積み上げて、円錐形のピラミッドを作ることにします。すると「底円が順次増加する円柱の和」を求めなくてはなりません。直接円柱の和を計算することはできませんから、円錐と四角錐との比を考えます。そのため、四角錐（ピラミッド）も、個数ではなく「量の和」として考え直すことにします。そこでまず次を証明します。   

四角錐の体積は同じ底面、同じ高さの直方体の 1/3 である

直方体、円錐、円柱の略記法

〔2-1 数と量〕で直方体に対する略記法を導入しました。復習をしておきましょう。円錐と円柱に対してはここで導入します。

□³(S, h) : 底面の面積が S の長方形で、高さが h の直方体
円錐(S, h) : 底面の面積が S の円で、高さが h の円錐
円柱(S, h) : 底面の面積が S の円で、高さが h の円柱

以下で、直方体といったときは、直方体を示すときと、その体積を示すときとがあります。円錐、円柱についても同様です。

高さの等しい直方体の体積は、その底面の面積に比例する

長方形は、底辺をそろえることでどちらが大きいかを判定できます。直方体の場合も同様で、任意の長方形 S₁, S₂、自然数 n、線分 h に対し次が成立します。

S₁ ＜ S₂  なら  □³(S₁, h) ＜ □³(S₂, h)
S₁ ＝ S₂  なら  □³(S₁, h) ＝ □³(S₂, h)
n□³(S₁, h) ＝ □³(nS₁, h)

次は、〔2-4 比の理論〕で述べた 比の等価性 の定義からすぐに得られます。証明は〔長方形の面積比〕と同様なので省略します。

現在の私たちにとっては、この定理は証明する必要もないほどあたりまえのことです。しかしこれは、「直方体の体積＝縦×横×高さ」と定義することができたからであって、この定義に至るまでには、数学の長い歴史があるのです。つまり古代では、量 a と自然数 n との積 na は

a ＋ a ＋ … ＋ a

と a を n個 合わせることで定義できたのですが、量と量との積は定義することができなかったのです。というより積を定義する必要がなかったのです。

高さの等しい円柱の体積は、その底面の面積に比例する

次に円柱を考えましょう。S が半径 r の円なら、〔2-5 円周と円の和〕の〔円と長方形〕定理より

S ＝ 〇²(r) ＝ □( \( \frac{c}{2} \), r)

と、Sは同じ面積の長方形で表されます。また、そこで示した証明から次が成立します。

円柱(S, h) ＝ □³(□( \( \frac{c}{2} \), r), h)

この式は、「円柱の体積は、底面が円 S と同じ面積の長方形で、高さが h の直方体の体積に等しい」ことを示しています。

これより次の定理が成立します。

量の列の和

「…に関する和」を「～に関する和」に還元する方法

比の理論では、よく「…は～に比例する」という語句がよく現れます。次の定理は、「…に関する和」を「～に関する和」に還元するための強力な手段で、以下ではたびたび用いられます。

定理は、比 A_i : B を分数 A_i/B とみなせば簡単です。〔2-4 比の理論〕で述べた〔比の和〕の定理を使っても簡単に証明できます。まず A₁ : B ＝ a₁ : b と A₂ : B ＝ a₂ : b から、(A₁＋A₂) : B ＝ (a₁＋a₂) : b が得られ、これと A₃ : B ＝ a₃ : b より (A₁＋A₂＋A₃) : B ＝ (a₁＋a₂＋a₃ ) : b が得られます。これを続ければ定理が示せます。

現在では比 A_i : B ＝ a_i : b は、A_i/a_i ＝ B/b と変形でき、A_i/a_i が一定であること、つまり「A_i は a_i に比例する」ことを意味しています。B と b は比にするために用いる適当な量です。

古代における”量”の扱い

現在は長さ（量）はメートル法で扱われますから、基準となる単位についていちいち言及する必要はありません。しかし古代では、そのつど単位を指定する必要がありました。たとえば A₁, A₂, …, A_n, B を長さ、a₁, a₂, …, a_n, b をお金とします。比は“何倍か”という概念の拡張なので

A_i : B = a_i : b, i = 1,2, … , n

は、「Bを単位として測った A_i の長さ ＝ b を単位とした a_i の金額」ですから、この関係は、合計 A₁＋A₂＋ … ＋A_n,と a₁＋a₂＋ … ＋a_n       に対しても成り立ちます。

四角錐の体積の求め方

四角錐の体積：計算方法のあらすじ

詳しい証明に入る前にまず簡単なあらすじを述べますから、おおざっぱに理解してください。現在のピラミッドは遠くから見るとでこぼこが消え、四角錐に見えます。これを階段ピラミッドと呼ぶことにします。階段ピラミッドは薄い直方体 V₁, V₂, … , V_n を積んでできる立体と考えてください。V_i の底面の面積は S_i で高さは h とすると、現在なら

V_i = h × S_i

と計算でき、その和は

V₁ + V₂ + … + V_n = h × ( S₁ + S₂ + … + S_n )

と簡単に計算できるのですが、古代では量同士の掛け算ができません。そこで先ほど説明した 「量の列の和」の定理を使うのです。S_i は正方形ですから、和 S₁＋S₂＋…＋S_n が計算できます。基準となる量はなんでもよいのですが、V_n と S_n としましょう。直方体の面積は底面積に比例しますから、以下で述べる式 (2) が成立します。正方形の面積の和は〔2-2 連続する正方形の和〕で計算しましたから、

S₁ + S₂ + … + S_n : n × S_n

の値がほぼ 1 : 3 であることが分かります。したがって、階段ピラミッドの体積

V₁ + V₂ + … + V_n

も、直方体の体積 n×V_n のほぼ 1/3 であることが分かります。以下では、このおおざっぱな議論を、“挟み撃ち論法”で正確にもとめます。

四角錐の体積と直方体の体積

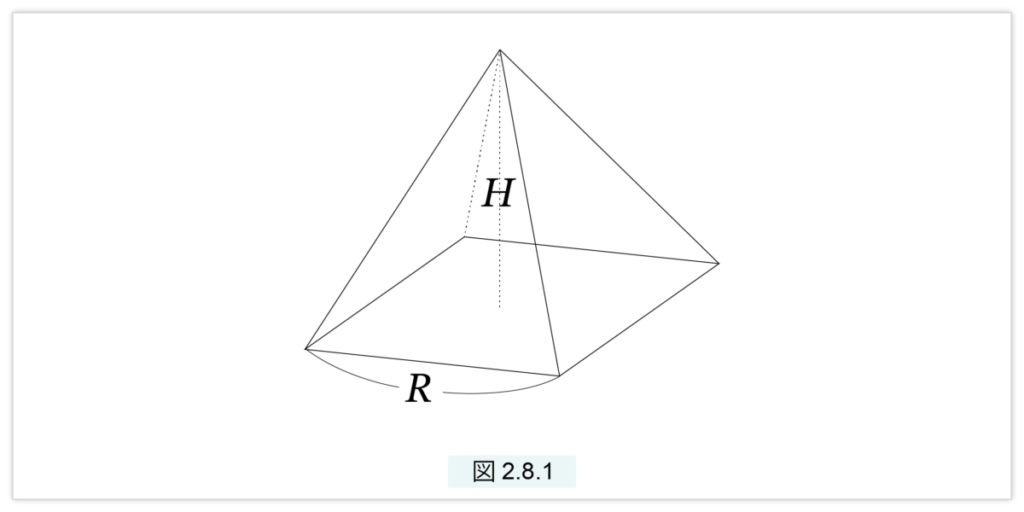
図2.8.1 で示された四角錐 W の体積を求めます。底面は、1辺がRの正方形、高さはH とします。nを自然数とし、r ＝ R/n、h ＝ H/n と置きます。i ＝ 1, 2, …, n に対し、

S_i ＝ □²(ir) 　　 1辺が ir の正方形
V_i ＝ □³(S_i, h)   底面が S_i 高さが h の直方体
V ＝ □³(S_n, H)   底面が S_n 高さが H の直方体

と置きます。〔1-4 ピラミッドの体積〕で議論したように、

V₁ ＋ V₂ ＋ … ＋ V_n-1 ＜ W ＜ V₁ ＋ V₂ ＋ … ＋ V_n                           (1)

が成立します。一方、上で述べた〔直方体の体積比〕より、

V_i：V_n ＝ □³(S_i, h) : □³(S_n, h) ＝ S_i : S_n ,   i＝1, 2, …, n

が成立しますから、〔量の列の和〕の定理 が適用でき

V₁ ＋ V₂ ＋ … ＋ V_n : V_n ＝ S₁ ＋ S₂ ＋ … ＋ S_n ： S_n                (2)

となります。正方形の和はすでに計算してあります。〔2-2 連続する正方形の和〕の〔正方形の和〕の定理の系より、

3{S₁ + S₂ + … + S_n }
 ＝ 3{□²(1r)＋□²(2r)＋…＋□²(nr)} ＞ (n＋1)□²(nr)

が成立します。よって、(2) の比の左項を3倍、右項をn倍すると

3×{V₁ ＋ V₂ ＋ … ＋ V_n} : n×V_n
＝ 3×{S₁ ＋ S₂ ＋ … ＋ S_n} : n×S_n

となります。n×V_n ＝ V、S_n ＝□²(nr) ですから

3×{V₁ ＋ V₂ ＋ … ＋ V_n} : V
＞ (n＋1)□²(nr) : n□²(nr) ＝ n＋1 : n ＞ 1 : 1

が得られます。分数で表わすと

V₁ ＋ V₂ ＋ … ＋ V_n > \( \frac{1}{3} \) V

が得られます。まったく同様にして

V₁ ＋ V₂ ＋ … ＋ V_n-1 < \( \frac{1}{3} \) V

が証明できます。これを合わせると

V₁ ＋ V₂ ＋ … ＋ V_n-1 < \( \frac{1}{3} \) V < V₁ ＋ V₂ ＋ … ＋ V_n

が得られます。n を大きくすると V_n はいくらでも小さくできますから、次が得られました。

W = \( \frac{1}{3} \) V

円錐の体積の求め方

円錐の体積：計算方法のあらすじ

円錐も水平面で何重にもスライスすると、薄い円柱に分解されます。これを“階段円錐”と呼ぶことにします。つまり、階段円錐とは、薄い円柱 C₁, C₂, …, C_n を積んだものです。円錐の体積を求めるには「円錐はほぼ階段円錐だ」とみなして、和 C₁＋C₂＋ … ＋C_n が計算できればよいわけです。〔2-5 円周と円の和〕では、円の面積の和が計算できることを示しました。これを使えば、上の議論と同様にして階段円錐の体積も計算できます。しかし、せっかく上で階段ピラミッドを議論しましたので、この結果を利用します。つまり、“円柱の和”を“直方体の和”に還元し、「階段円錐は円柱の 1/3」という結果を「階段ピラミッドは直方体の1/3」という結果から比の理論を利用して得ることにします。

円錐の体積と直方体の体積

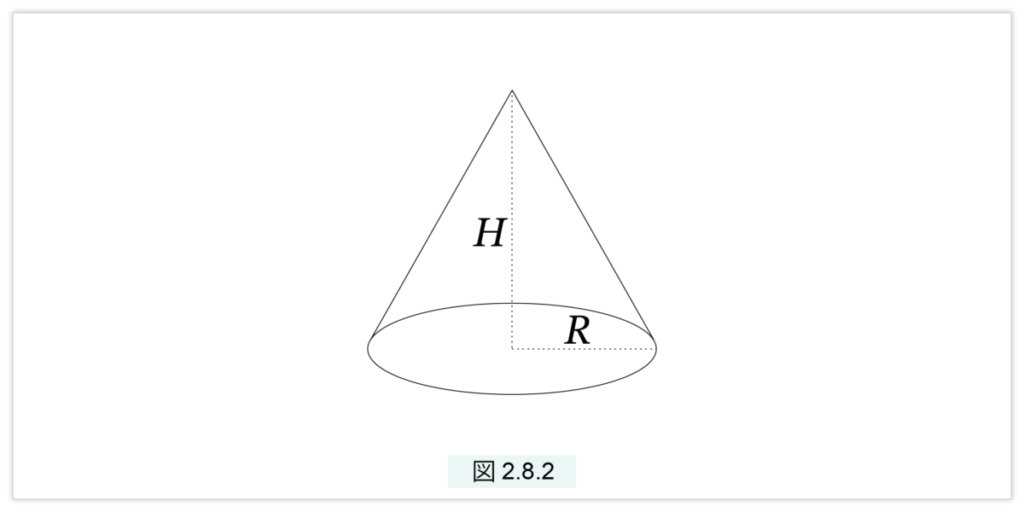
図2.8.2 で示された円錐 E の体積を求めます。

底面は、半径 Rの円、高さはH とします。nを自然数とし、r ＝ R/n、h ＝ H/n と置きます。i ＝ 1, 2, …, n に対し、

S_i ＝ 〇²(ir) 半径 ir の円
C_i ＝ 円柱(S_i,h)   底面が S_i の円で、高さが h の円柱
C ＝ 円柱(S_n,H)   底面が S_n の円で、高さが H の円柱
V_i ＝ □³(S_i,h) 底面が S_i の正方形で、高さが h の直方体
V ＝ □³(S_n,H) 底面が S_n の正方形で、高さが H の直方体

と定めます。四角錐と同様、次が成立します。

C₁＋C₂＋ … ＋C_n-1 ＜ E ＜ C₁＋C₂ ＋ … ＋C_n                                 (4)

定理〔円柱の体積比〕と〔直方体の体積比〕から次が成立します。

円柱(S_i,h)：円柱(S_n,h) ＝S_i：S_n ＝ □³(S_i,h)：□³(S_n,h),    i＝ 1, 2, …, n

すなわち

C_i：C_n ＝ V_i：V_n

よって、〔量の列の和〕の定理 が適用でき、

C₁＋C₂＋ … ＋C_n：C_n ＝ V₁＋V₂＋ … ＋V_n ：V_n

両辺の右項をn倍します。

nC_n ＝ C、nV_n ＝ V ですから

C₁＋C₂＋ … ＋C_n：C ＝ V₁＋V₂＋ … ＋V_n：V

上で、

V₁＋V₂＋ … ＋V_n：V ＞ 1:3

を示しました。よって、

C₁＋C₂＋ … ＋C_n：C ＞ 1:3

が成立します。同様にして

C₁＋C₂＋ … ＋C_n-1：C ＜ 1:3

が示されます。まとめると

C₁＋C₂＋ … ＋C_n-1：C ＜ 1:3 ＜ C₁＋C₂＋ … ＋C_n：C

となります。一方 (4) より

C₁＋C₂＋ … ＋C_n-1：C ＜ E：C ＜ C₁＋C₂ ＋ … ＋C_n：C

が得られます。C_n は高さが h＝H/n の円柱ですから n が大きくなるといくらでも小さくなります。よって、

円錐 E：円柱 C ＝ 1：3

となり、「円錐の体積は同じ底面、同じ高さの円柱の 1/3 である」ことが証明されました。

アルキメデスは、円錐の体積が同じ高さで同じ底面積の円柱の 1/3 であるという結果を、円錐を薄い円柱にスライスして求めました。この方法は後世にとても大きな影響を与えることになります。