小石の数理
アルキメデスの面積と体積
放物線の求積
2-6. 等積変換とは?内項外項の定理・グノモンの定理を詳しく解説
第1章では、ピラミッドの体積を求めるのに「小石の数理」を用いました。(詳しく知りたい方は〔1-3 小石の数理〕をご一読ください。)しかし、アルキメデスは小石の数理(整数論)は使わずに、すべて「比の理論」を使って議論しています。現在では、面積は「小さな正方形がいくつでおおえるか」で議論できます。しかしこれは“後智慧”で、当時は数の “1” はこれ以上小さく分けることはできなかったのです。〔2-3 πの源流〕で見たように、円周とか円の面積は、円を 1/6, 1/12, … と小さく割っていくことで計算しています。量は数と違って、割ることができるのです。ここでは面積に関してもう少し詳しく見てみましょう。
ページ目次
等積変換
三角形は、同じ面積の長方形に変換できます。面積を変えずに変換することを等積変換といいます。たとえば次は等積変換です。
底辺が a 高さがh の三角形
\( = \frac{1}{2}□(a. h) = □(a. \frac{h}{2} ) \)
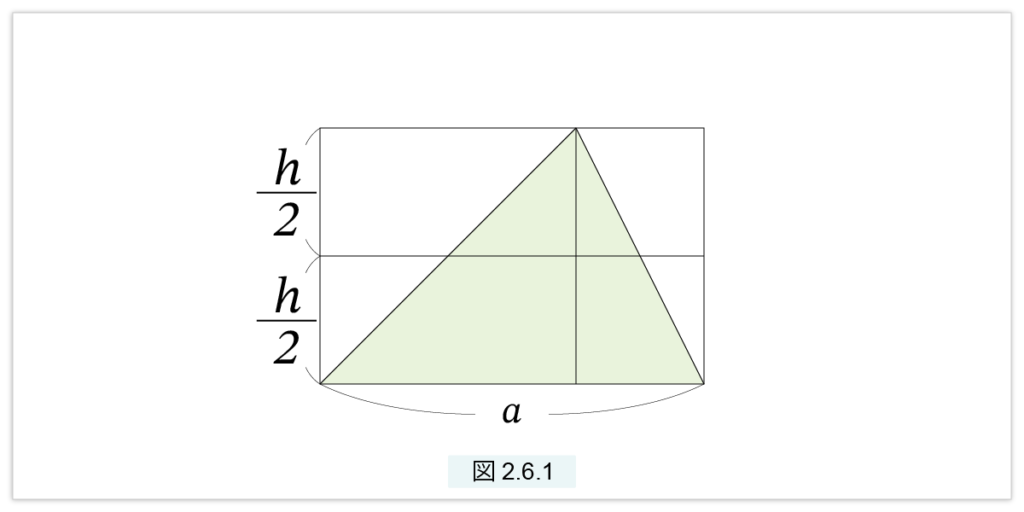
この式の意味は「底辺が a で高さが h の三角形の面積は、底辺が a で高さが h/2 の長方形の面積に等しい」という意味であって、「三角形の面積=底辺×高さ/2」という現代の公式とは意味が異なります( 図2.6.1)。 古代の比とは、2倍、3倍、1/2、1/3 の拡張概念であって、現在の分数のような「演算システム」ではありませんでした。
三角形の相似
「三角形の相似」の条件
おそらく読者の皆さんは、三角形の相似のことはよく知っていると思います。次の定理の3つの条件の1つが成り立てば、2つの三角形は相似です。証明は省略します。
【定理】三角形相似
2つの三角形において次の3つの条件は同値である。
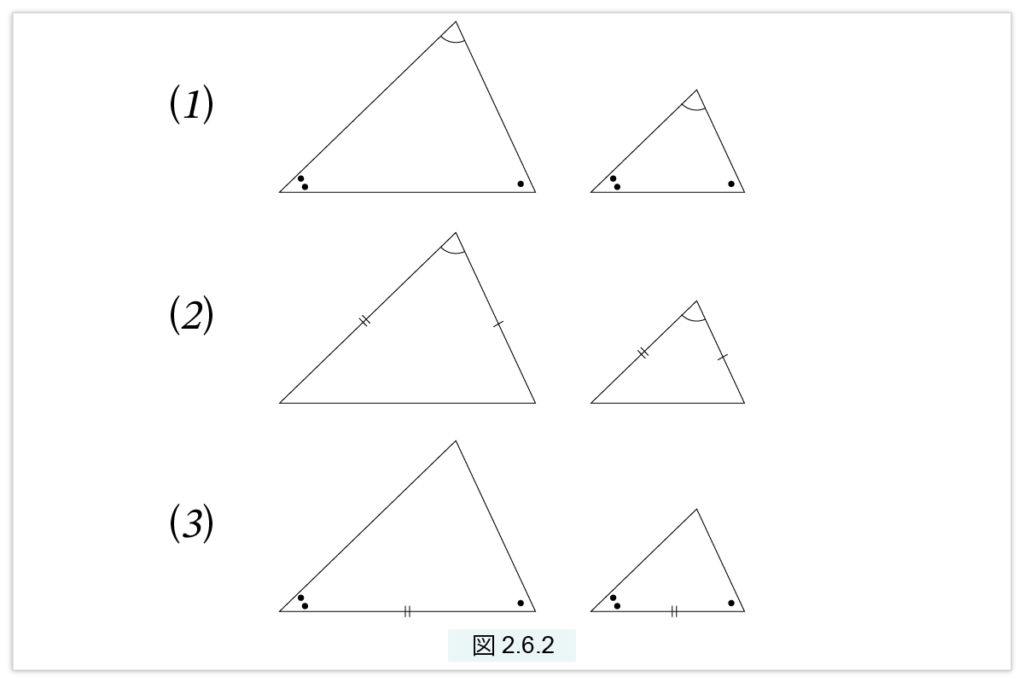
(1) 対応する3つの角が等しい。
(2) 対応する1つの角と、それを挟む2つの辺の比が等しい。
(3) 対応する一つの辺の比と、その両端の角が等しい。
三角形の底辺平行
比の理論で最も重要な働きをするのは次の定理です。これも証明は省略します。
【定理】三角形底辺平行
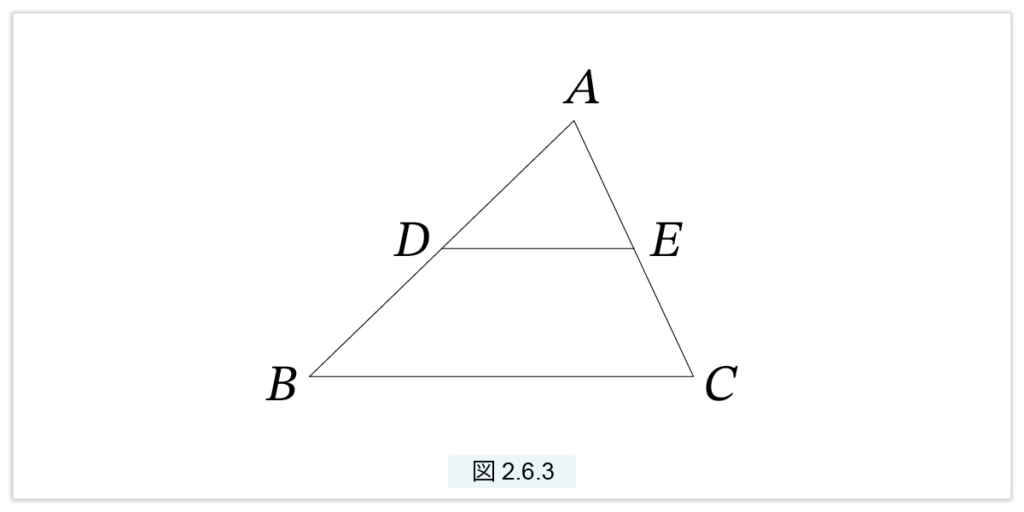
図2.6.3 において次が成立する
DE と BC は平行 ⇔ AD : AB = AE : AC
L字型の図形「グノモン」
グノモンの定理とは
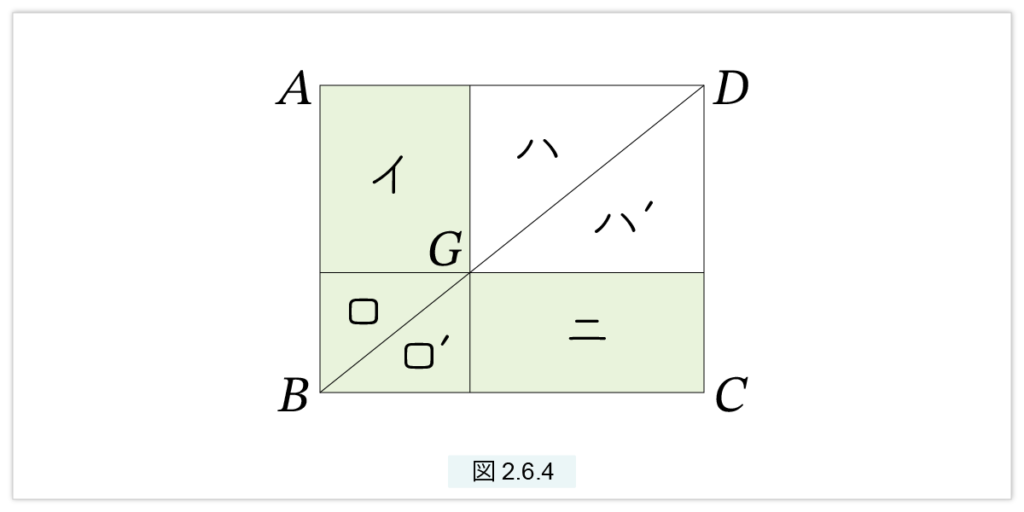
図2.6.4 を見てください。ABCD は長方形で、G は対角線上の点、G を通る AB と平行な直線と、BCと平行な直線が書かれています。このときできる L字型の図形 イ-ロ-ロ’-ニ をグノモンといい、イとニをグノモンの突起部といいます。
「グノモンの定理」の証明
【定理】グノモン
グノモンの突起部は等しい。
図2.6.4 で (イ)=(ニ) が成り立つことを示します。BD は長方形の対角線ですから
(イ)+(ロ)+(ハ) = (ニ)+(ロ’)+(ハ’)
(ロ)=(ロ’), (ハ)=(ハ’)
よって (イ)=(ニ) が成立します。
内項外項の定理の証明
〔2-4 比の理論〕で述べた〔内項外項〕の定理 を証明しましょう。
【定理】内項外項
線分 a, b, c, d に対し、次が成立する。
a : b = c : d ⇔ □(a, d) = □(b, c)
まず、a : b = c : d と仮定しましょう。□(a, d) と □(b, c) を図2.6.5 のように置きます。
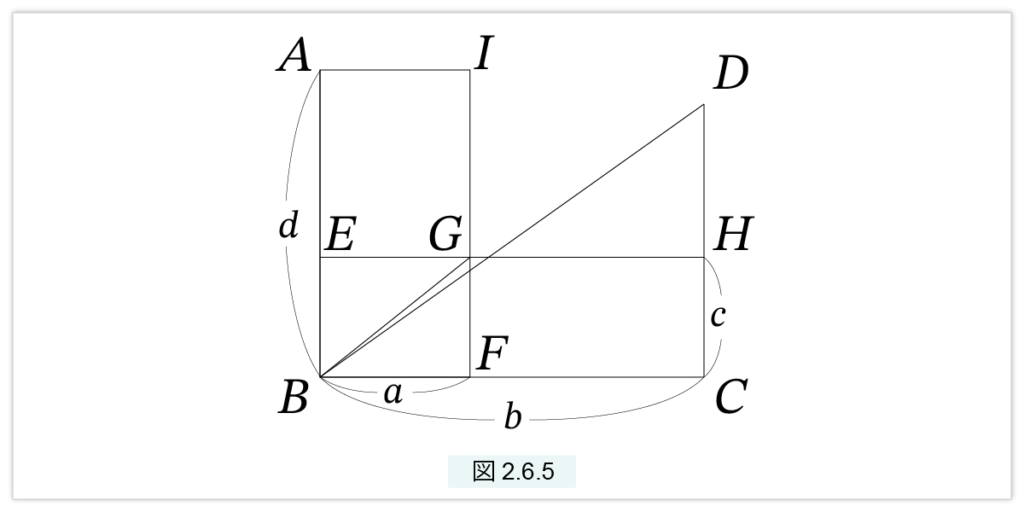
ABFI が □(a, d) で、EBCH が □(b, c) です。CH の延長上に点 D を CD=d となるようにとり、D と B を結びます。IFとEHの交点をG とします。すると、△BFG と △BCD において、
BF:BC = a : b, FG : CD = c : d
ですから、仮定 a : b = c : d より、
BF : BC = FG : CD
となり、2つの三角形は相似となります。よって、∠DBC = ∠GBF となり、G は対角線DB 上になければなりません。すると、2つの長方形で作るL字形はグノモンとなり、〔グノモン〕の定理より、この2つの長方形は等しくなります。
次に、□(a, d) = □(b, c) と仮定しましょう。2つの長方形を同じように重ねます。( 図2.6.6 )。
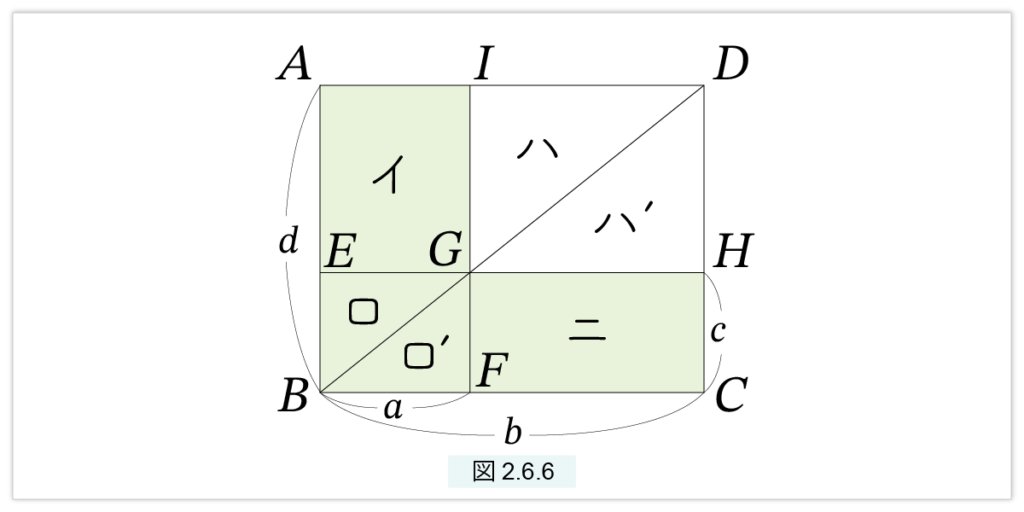
CH の延長線と AI の延長線の交点を D とします。仮定より、(イ)=(ニ) が成立します。明らかに (ロ)=(ロ’), (ハ)=(ハ’) です。すると、
(イ)+(ロ)+(ハ) = (ニ)+(ロ’)+(ハ’)
となり、DGB は長方形の対角線でなければなりません。すると△GBF と △DBC は相似となり
a : b = BF : BC = GF : DC = c : d
となります。
長方形の和
底辺の等しい長方形は、積み上げることによって足すことができます。底辺をそろえるには次の定理を使います。
【定理】長方形の和
任意の線分 a, b, c に対し、次を満たす線分 x が作図できる
□(a, b) = □(x, c)
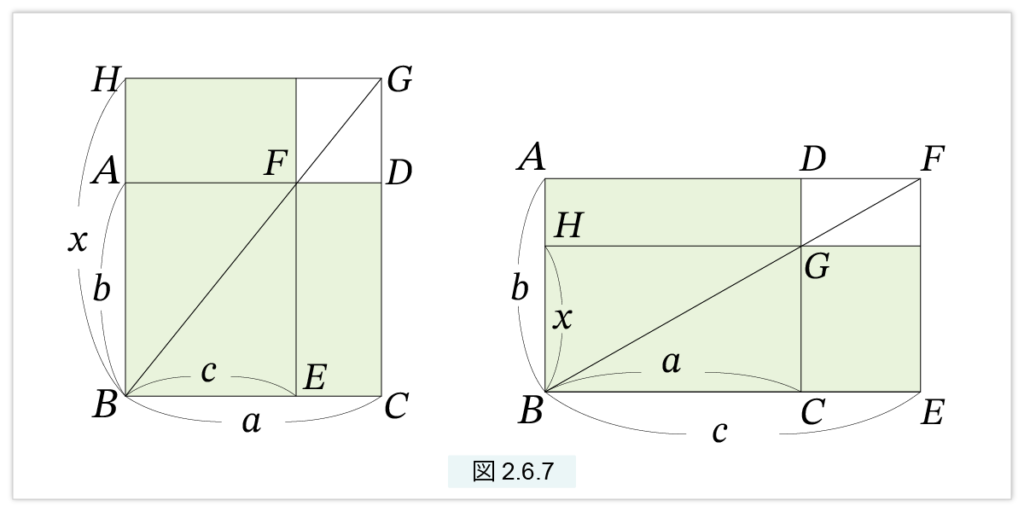
図2.6.7 の長方形ABCD で、AB=b, BC=a とします。直線BC上に点E を、BE=c となるように取ります。直線 BC と言った場合、線分 BC を左右に無限に延長した直線を意味します。c<a の場合は線分 BC 上に、c>a の場合はBC の延長線上に点 E を取ります。E を通る、直線AB と平行な直線を引き、直線AD との交点を F とします。F と B を結び、直線BF と直線CD の交点を G とします。G から直線BA に下ろした垂線の足を H とします。BH=x が求める線分です。
BH=x が定理の条件を満たすことは、図2.6.7 の影の部分がグノモンとなっていることから分かります。
まとめ
ここでは三角形と長方形が足せることを示しました。三角形は長方形に等積変換できます。また、2つの長方形は底辺をそろえることで、足すことができます。したがって、任意個数の三角形は長方形に等積変換できることになります。また、この節で証明した〔内項外項〕の定理 は、比の理論においてとても重要な役割をします。

