第18回 万年カレンダー：織田信長の誕生日は？

万年カレンダー：通日の考え方

今回のお話では万年カレンダーという便利なカレンダーを紹介しましょう。万年カレンダーとは次の整数列

1, 2, 3, …   

のことです。読者の皆さんのなかには、拍子抜けした方もいるかもしれません。しかし古代史とか古代の天文学にはとても便利なカレンダーなのです。これはユリウス暦とグレゴリオ暦の両方で用います。ユリウス暦の場合は“1”は「西暦1年1月1日」を、グレゴリオ暦の場合は“1”は「西暦1年1月3日」を意味します。つまり、この万年カレンダーは前回のお話で述べた通日のことなのです。すると、ニュートン※は、ユリウス・カレンダーでは 599,734日生まれ、グレゴリオ・カレンダーでは 599,732日生まれとなります。この万年カレンダーを使えば、たとえばイタリアのガリレオ※と日本の織田信長など、当時採用されていた暦が違っていたとしても、どちらが何日年上かを簡単に計算できます。

グレゴリオ暦の万年カレンダーの“１” は西暦1年1月3日にあたります。偶然にも、この日は月曜日なのです。そこで万年カレンダーを次のように並べてみました。

万年カレンダーには年や月はありませんから、閏年とか小の月、大の月などもありません。曜日もありません。1,2,3,…を7つごとに折り返しただけです。

暦と数学

割り算

ここで数式の復習をしましょう。「数学は式ばかり現れるから嫌いだ」ということをよく聞きます。数学の解説書では、なるべく式を使わずに書かれたものもあります。語学では、「新しい単語を習得するには何十回もその単語に出会う必要がある」といいます。数式も同様で、何度もその数式を使って練習する必要があります。 　

a と b を正の整数とします。次の2種類の割り算を使い分けします。答えを小数で求める割り算を a/b で、答えを整数と余りで求める割り算を a ÷ b で表します。たとえば「14割る3」は

14/3 = 4.333 … ,
14 ÷ 3 = 4 ･･･ 2

となります。一般に

a ÷ b ＝ q … r 　　　(1)

のとき、q を a を b で割った商、r を余りといいます。(1) が成立する必要十分条件は、次の (2) が成立することです。

a = qb + r, 0 ≦ r < b　　　(2)

剰余計算 — mod

a を b で割った余りを a mod b で表します。mod を剰余計算といいます。

x を正の実数とします。このとき [x] で、x の整数部分を表します。つまり

[ x ] = x の整数部分

です。現在の電卓には剰余計算 mod が計算できる機能を持っているようですがなければ次のように計算します。a/b の整数部分 [a/b] を x、小数部分を y とおくと、

a/b ＝ x ＋ y,  0 ≦ y ＜ 1　　　(3)

と表せます。(3) の左の式の両辺を b倍すると

a ＝ xb ＋ yb

となります。0 ≦ y ＜ 1 より 0 ≦ yb ＜ b となります。この式を (2) と比較すると

q ＝ x ＝ [a/b],  r ＝ yb

が得られます。つまり、剰余 r は a/b の小数部分をb倍して得られます。

たとえば a＝14, b＝3 の場合、14 ÷ 3 の商 q と剰余 r は、a/b ＝ 4.66… より次のように求めることができます。

q ＝ [4.66…] ＝ 4,
r ＝ 0.66… × 3 ＝ 1.99… ＝　2

この演算を用いれば、ユリウス通日とグレゴリオ通日は次のように表すことができます。

ユリウス暦 n ＋ 1年1月0日のユリウス通日
＝ n × 365 ＋ [n/4]

グレゴリオ暦 n ＋ 1年1月0日のグレゴリオ通日
＝ n × 365 ＋ [n/4] – [n/100] ＋ [n/400]

万年カレンダーで曜日を求める

曜日のコード

上の表18-1の万年カレンダーを見てください。日曜日は 7, 14, 21, … と7 の倍数になっています。月曜日は 8, 15, 22, … と「7の倍数＋1」の形です。ここで、日、月、火、水、木、金、土のそれぞれに数値 0, 1, 2, 3, 4, 5, 6 を割り当てます。各曜日 x に割り当てられた数値 n をその曜日のコードといい、code(x) ＝ n と書きます。逆に x を n が表す“曜日”といい、「曜日(n)＝x」 と書きます。たとえば、

code(火) ＝ 2, 
曜日(2) ＝ 火

となります。7 以上の自然数 n に対しては

曜日(n) ＝ 曜日(n mod 7)

と定義します。

　皆さんは「3 を 7 で割った余り」つまり、「3 mod 7」 は何か分かりますか。式 (2) で a＝3, b＝7, q＝0, r＝3 とおくと成立します。したがって、「3 を 7 で割った商は 0、余りは 3」となります。同様に 0 mod 7 ＝ 0 となります。

2027年10月19日は何曜日か

2027年10月19日が何曜日かを計算してみましょう。まず2027年1月0日のグレゴリオ通日を計算します。

2026/4 ＝ 506.5

ですから

[2026/4] ＝506,
[2026/100] ＝20,
[2026]/400 ＝5

となります。よって、2027年1月0日の通日は

2026 × 365 ＋ 506 – 20 ＋ 5 ＝ 739,981

となります。

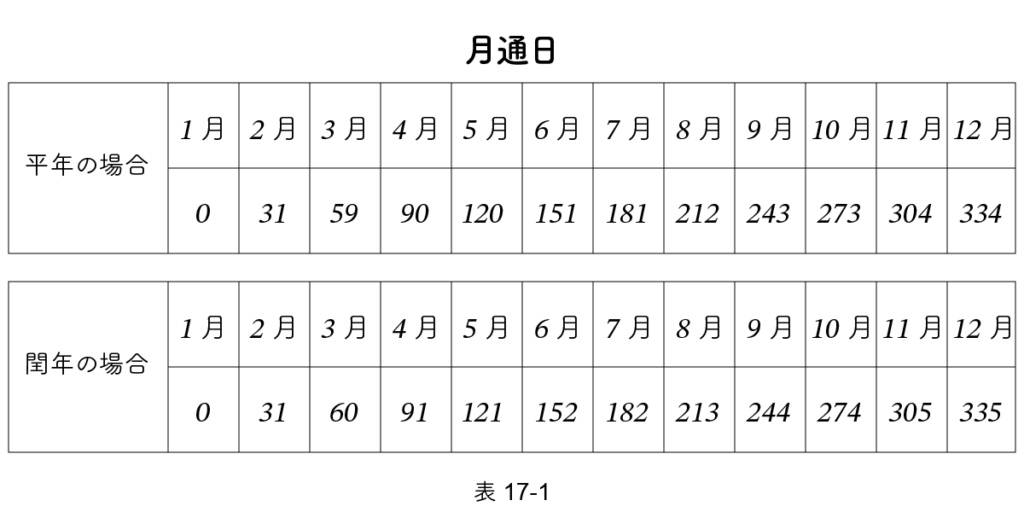
10月の月通日を上の表で引くと、273 ですから2027年10月19日の通日は

739,981＋273＋19＝ 740,273

となります。これより、2027年10月19日の曜日は

曜日(740,273)＝ 曜日(740,273 mod 7) ＝ 曜日(2) ＝ 火

となります。

昭和21年6月3日は何曜日か

この方法を使えば、昭和でも平成でも令和でも、次のような西暦との対応さえ分かれば曜日が簡単に計算できます。

昭和1年 ＝ 1926年、
平成1年 ＝ 1989年、
令和1年 ＝ 2019年

明治の改暦以来、日本の暦はグレゴリオ暦であり、元号は単なる名称です。たとえば昭和は、1926年12月25日からであり、12月25日以前は大正です。したがって通日の計算では、昭和1年1月0日が存在するとして計算できます。あるいはむしろ、

昭和0年 ＝ 1925年

と記録しておくと、

昭和 x年 y月 z日 ＝ グレゴリオ暦 1925＋x年 y月 z日

と簡単に計算できます。昭和21年6月3日が何曜日だったかを計算しましょう。グレゴリオ暦に直すと 1946年6月3日になります。1946年1月0日の通日は

1945÷4＝486.25,
[1945/4]＝486,
[1945/100]＝19,
[1945/400]＝4,
∴     1945×365＋486 – 19 ＋4 ＝ 710,396

6月の月通日は151日ですから、1946年6月3日の通日は

710,396＋151＋3 ＝710,550

曜日(710,550)＝ 曜日(710,550 mod 7) ＝ 曜日(1) ＝ 月

織田信長の誕生日は？– 旧暦の場合を考える

改暦前は旧暦なので注意が必要です。たとえば

文政 1年 1月 1日 ＝ グレゴリオ暦 1818年 2月 5日

のように、旧暦の月は西暦の月とは対応がとれていません。各年号の元年に対し、この例のように右辺のグレゴリオ通日を記録しておくとよいでしょう。文政元年は 1583年以後ですからグレゴリオ暦ですが、それ以前はユリウス暦であることに注意してください。たとえば織田信長の誕生日は

天文 3年5月 12日 ＝ ユリウス暦 1534年6月23日

であり、右辺はユリウス暦です。したがって、ユリウス通日を求めます。1534年1月0日のユリウス通日は

1533×365＋[1533/4] ＝ 559,928

となります。6月の月通日は 151ですから1534年6月23日のユリウス通日は

559,928＋151＋23＝560,102

となります。戦国時代には曜日はありませんが、あったとして信長の生まれた日の曜日を求めてみましょう。グレゴリオ通日はユリウス通日から2引けば求まりますから、

曜日((560,102 – 2) mod 7) ＝ 曜日(2) ＝ 木

となります。