第22回 月齢の計算

月の満ち欠けの数理

月の呼び名

月の満ち欠けの形にはいろいろな呼び名があります。三日月、十三夜、十五夜（満月、望月(もちづき)）、十六夜(いざよい)、上弦、下弦、など。本連載では、太陽・月・地球と一直線に並んだ時の月の相を朔(さく)月と呼び、その次の日を新月と呼ぶことにしています。歴史的には、月が消えてからふたたび生まれる日、つまり夕方西の空に太陽が沈んだ直後に再び姿を現した月のことを、一般に新月と呼んでいたからです。また“朔(さく)”という漢字はもとに戻るという意味もありますが、遡(さかのぼ)るという意味もありますから、最初に見えた日を1日遡(さかのぼ)るという意味でこのように呼ぶことにしました。

月齢とは

学術的には、月の相は月齢(げつれい)と呼ばれる実数で表されます。学術的な月齢は、前回の朔月からその日の正午 12:00 までの日数を表します。この方法だと、その日の10:00 に朔月になったとすると、月齢は 2時間＝ 0.08日となりますが、14:00 だと –2時間 ＝ –0.08日と、マイナスになってしまいます。これだと初心者は扱いにくいので、本連載では深夜の 24:00 を基準として深夜月齢を考えることにしました。

日・時・分の変換

ここで、単位の“日”“時”“分”の復習をしておきます。たとえば「5日4時間32分」を“日”で表しましょう。「1時間＝60分」ですから、「32分＝ 32/60時間＝ 0.533時間」。「1日＝24時間」ですから、

5日4時間32分 ＝ 5日4.533時間 ＝ 5日 4.533/24 日
＝ 5.1889 日

となります。こんどは逆に 5.1889日を“時・分”に変換してみましょう。

5.1889日 ＝ 5日 0.1889×24 時間 ＝ 5日 4.5336時間
＝ 5日4時間 0.5336×60分 ＝ 5日4時間 32.016分

と（ほとんど）もとに戻ります。

以下では、月齢は深夜月齢のこと、つまり、前回の朔月からその日の 24:00 までの経過日数を表すものとします。たとえば、月齢が 5.1889 であるとは、前回の朔月からその日の24:00 までに、5日と4時間32分が経過したことを表します。

剰余計算（正の実数）

前回の朔月から次の朔月までの期間を1朔望月といいます。

1朔望月 ＝ 29.53059日

実は、1朔望月は平均値なのですが、しばらくは均等にこの期間で朔月が巡ってくるとして議論します。起点はなんでもよいのですが、これまでどおりグレゴリオ通日とします。グレゴリオ通日に朔月が何個入り、どのくらい余るかを考えます。〔第18回 万年カレンダー〕では、自然数を自然数で割った余り（剰余）を考えました。これを正の実数に拡張します。

a と b を正の実数とします。すると次を満たす非負整数 n と r が存在します。

a ＝ nb ＋ r,   0 ≦ r ＜ b                                              (1)

n を、a を b で割った商、r を余り（剰余）といいます。n を非負整数としたのは、a ＜ b のとき n ＝ 0 となるからです。このとき r＝a です。

長さ a と b の2本のロープを考えます。式 (1) は、ロープ a からロープ b が n本とれ、r 余ることを意味します。a＝5.8, b＝1.1 としましょう。

5.8 / 1.1 = 5.272727 ･･･
5.8 = 5.272727 ･･･ × 1.1 = 5 × 1.1 + 0.272727 × 1.1
= 5 × 1.1 + 0.2999997

となります。つまり、長さ 5.8 のロープから長さ 1.1 のロープが5本取れ、0.3 余るということになります。上の計算で余りが 0.299997 となったのは、5.8/1.1 の計算結果の小数部をあるところで四捨五入したためです。関数電卓などで計算する場合は、計算結果の 5.2727… から整数部の 5 を引いて、その結果に除数 1.1 を掛けると 0.3 が得られるものが多いと思いますが、こういった計算に誤差はつきものだと考えたほうがよいと思います。

月齢の計算

グレゴリオ通日と朔望月

さて、西暦1900年の1月1日22時51分が朔月でした。これを利用しましょう。まず1900年1月0日のグレゴリオ通日を計算しましょう。

1899/4 ＝ 474.75, 
[1899/100]＝ 18,
[1899/400]＝ 4

ですから、グレゴリオ通日は

1899×365＋474 – 18 ＋ 4 ＝ 693,595

となります。1月1日はこれに1足した数です。これを１朔望月で割った余りを計算します。

693,596 ÷ 29.53059 ＝ 23487.3736
0.3736×29.53059 ＝ 11.03262842

すると、1900年までに1朔望月が 23487回あり、11.03日余ります。通日から 11.03日引いて計算すると余りは 0 となります。月齢 0 は24:00 に朔月になったということですが、実際はもう少し前の 22:51 ですから、11.03 は引きすぎです。そこで 10.7 引くことにします。つまり、月齢を次の式で計算することとします。

【月齢の計算式】
（グレゴリオ通日 – 10.7）を1朔望月 29.53059 で割った余り

現在の皆さんは電卓とかコンピュータが使えますから、大きな桁数の計算もできると思います。昔から月齢の計算はいろいろな方法が考えられてきましたが、それらはたいてい表を使った計算です。現在のコンピュータは大量のメモリーが使えますから、たとえば2000年分のデータを記憶しておくことなどなんでもありません。ここで上の公式を述べたのは、「暦の数理」を理解してもらいたかったからです。

2030年3月3日の月齢

たとえば、2030年3月3日の月齢を計算してみましょう。2030年1月0日のグレゴリオ通日は

2029×365＋ 507 – 20 ＋ 5 ＝ 741,077

ですから、3月3日の通日は

741,077＋31＋28＋3 ＝ 741,139

したがって月齢は上の公式より、

(741139 – 10.7)/29.53059 ＝ 25096.96894
0.96894×29.53059 ＝ 28.61336

となり、3月3日の月齢は 28.6 となります。したがって、次の日は 29.61 となりますが、1朔望月は 29.53 で終わりですから、次の日4日の月齢は

29.61 – 29.53 ＝ 0.08

となります。

1朔望月の変動

上で計算される月齢は単なる近似値で実際に観測される月齢値ではありません。しかし、人間の目で観測した場合月齢1日の差はほとんど見分けがつきません。月齢は0日から始まっていますから、上の近似値はおおよそ次の対応があると考えてよいでしょう。

0～1日：朔、　7～8日：上弦、　14～15日：満月、　21～22日：下弦

上の公式が誤差を含むのは、1朔望月が平均値であって、実際には変動するからです。変動の原因はいろいろありますが、主な原因に地球の公転面と月の公転面が同一平面ではなく、ほんの少し（5度ほど）角度を持っていることがあります。

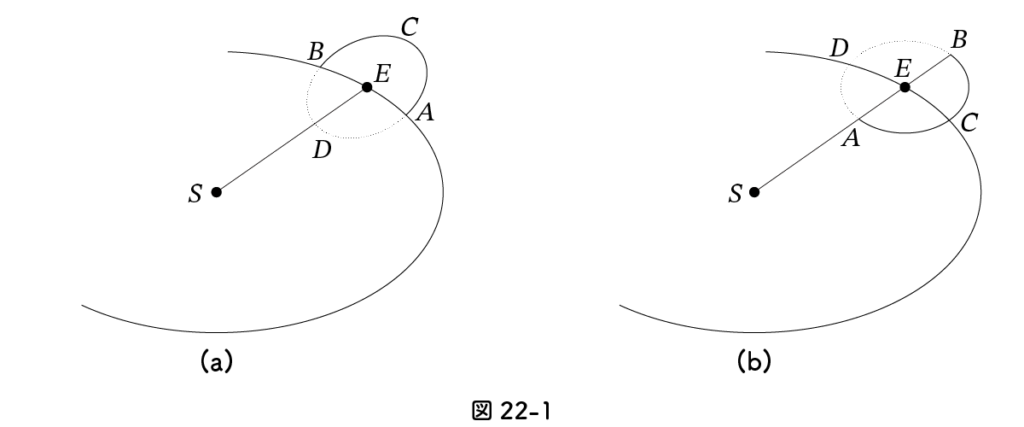
図22-1で、S は太陽 E は地球、ACBD は月の軌道です。A と B は地球の軌道面にあります。A を昇交点、B を降交点といいます。しかし C と D は地球の交点面上にはありません。(a) では真上から見た場合、SDEC は一直線上にありますが、日食も月食も起きません。一方 (b) では A で日食が起き、B で月食が起きます。

天球モデル

図22-1は太陽系モデルですが、今度は天球モデルを考えましょう。毎晩夜の 24:00 に南の空を眺めていると思ってください。星々は毎日約1度、東から西に移動します。1度は日周に換算すると 24/360時間 ＝ 24×60/360分 ＝ 4分 です。こんどは毎日4分ずつ時間を進めてみましょう。つまり、最初の夜は 24:00、次の夜は 23:56、… と観測します。すると天球は固定され同じ星空が広がり、一日ごとに月や太陽は西から東に移動します。太陽の通る道を黄道、月の通る道を白道といいます。黄道は地球の公転軌道を、白道は月の公転軌道を表しています。黄道と白道の交わる点が昇交点と降交点です。黄道は天球に固定されていますが、白道は移動します。つまり、昇交点と降交点は東から西へ移動するのです。月の公転に関しては次の3つの数値があります。

1朔望月＝ 29.53059日
1恒星月 ＝ 27.3216615日
1交点月 ＝ 27.212221日

昇交点は、月が黄道を下から上に通過する点で、降交点は上から下に通過する点です。1恒星月とは、月が再び天球上の元の位置に戻ってくるまでの期間です。1交点月とは、月が昇交点を出発して、反対側の降交点を横切り、ふたたび昇交点にまで戻るまでの期間です。1恒星月と比べ、約 0.1日短いのは、昇交点が黄道上を西に移動するからです。1恒星月で、月が天球の元の位置に戻ってきたとき、太陽も進んでいますから、月が元の形に戻るまでにはあと約2日かかります。 1恒星月と1交点月の差は 0.1日とわずかですが、無視できるほど小さくはありません。また地球から月までの距離と、地球から太陽までの距離の比は 1 : 400 と大きいのですが、これも無視できません。つまり図22-1で、(a) の場合と (b) の場合では、太陽と月の間の引力の変化のしかたが異なるのです。それでは月の運行において、昇交点の位置が同じ状態に戻る期間はどのくらいなのでしょうか。次を満たす自然数 n と m を求めましょう。

n × 朔望月 ≒ m × 交点月

実際 n＝223、m＝242 とすると次のようにほとんど一致します。

223×29.5306日 ＝ 6585.3238日
242×27.2122日 ＝ 6585.3524日

400年に1回の例外を除くと、18年に4回の閏年があるので

18年11日8時間 ＝ 18×365＋4＋11 ＋ 8/24 日
 ＝ 6585.3333日

となり、上の数値とほとんど一致します。 　

「18年と11日と 1/3日」をサロス周期といいます。これについてはまた「日食のお話」のところで議論しましょう。

サロス周期ごとに月齢は繰り返されるのですが、「11日と 1/3日」が余分です。都合のいいことに、12朔望月（1太陰年）の 29.5×12 ＝ 354（日）をこれに加えると 365と1/3日となり、これはほぼ1太陽年です。〔第11回 メトン周期の正体〕で述べたように、19太陽年がちょうど 235朔望月となり、月の相（月齢）もだいたい19年ごとの繰り返しとなります。

このお話の最初に述べた方法は、1朔望月の値が一様だという仮定のもとでの方法で、実際には1朔望月の値は複雑に変動します。より正確な月齢の計算は次の公式で計算できます。

【正確な月齢の計算式】
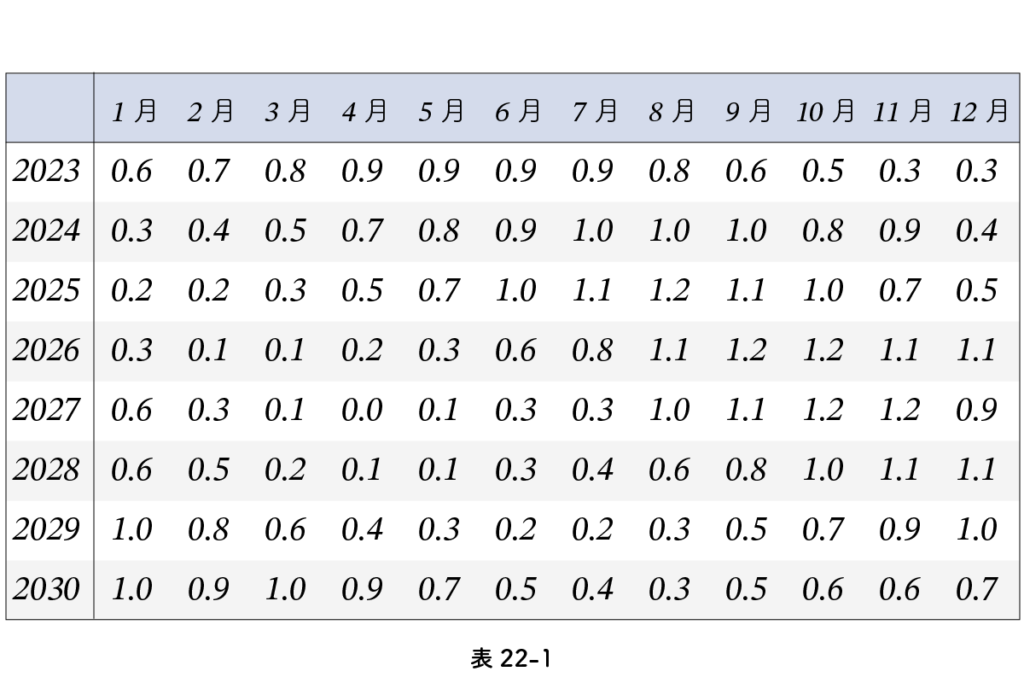
（グレゴリオ通日 – 11.3 ＋α）を1朔望月 29.53059 で割った余り

ここで、αは月齢を求める日時の補正値で、表22-1から持ってきます。