小石の数理
アルキメデスの面積と体積
放物線の求積
1-4. 四角錐の体積|ピラミッド建設でも使われた四角錐の体積の公式
前節〔1-3 小石の数理〕では砲弾を並べて三角数や三角錐数の性質を考えました。今回は四角錐の体積について考えてみましょう。
ページ目次
四角錐数と準立方体
四角錐数:平方数の数列の級数
平方数の数列の級数を考えます。平方数の数列は、以下です。
12, 22, 32, 42, …
この級数の各要素を四角錐数と呼びます。現在の私たちは、次の公式をよく知っていると思います。
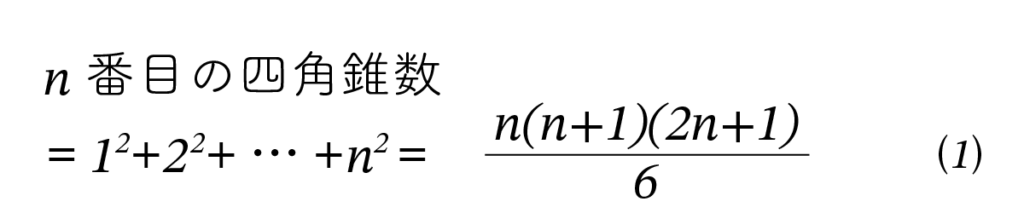
四角錐数と準立方体の関係 〜 準一般的な証明 〜
図1.4.1は4番目の四角錐数です。四角錐数と呼ぶよりは、“ピラミッド数”と呼んだ方がよいかもしれません。
古代の人は (1) のような式は使えませんから次のように表現しました。
n番目の四角錐数×6 = (n – 1)番目の準立方体 + n番目の準立方体 (2)
古代では変数 n は使えませんから n=5 の場合を示します。しかしこの5は特定の自然数を表すのではなく一般の自然数を代表しているのです。このような証明を準一般的な証明といいます。
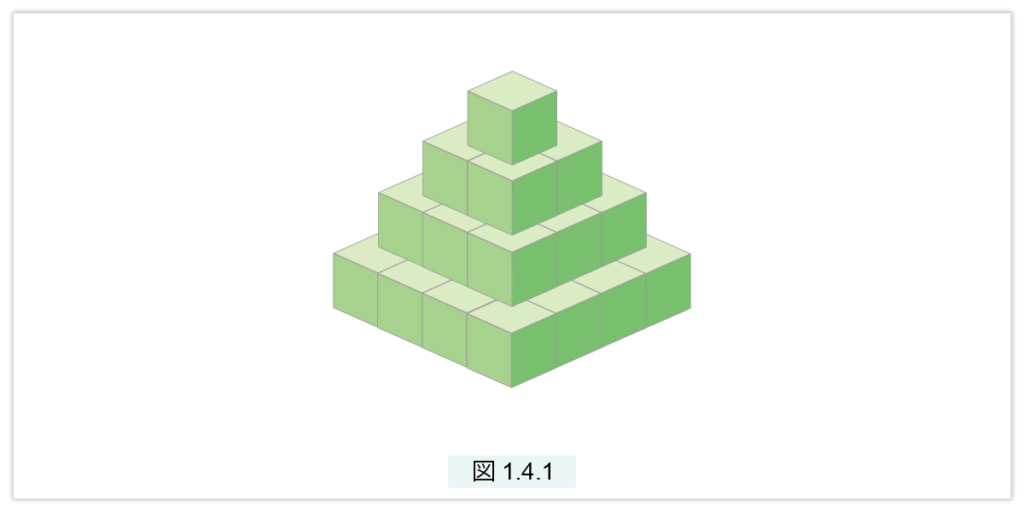
この証明に、前節で議論した次を使います。
隣り合う2つの三角数の和は平方数になる(図1.3.10 – 再掲)。
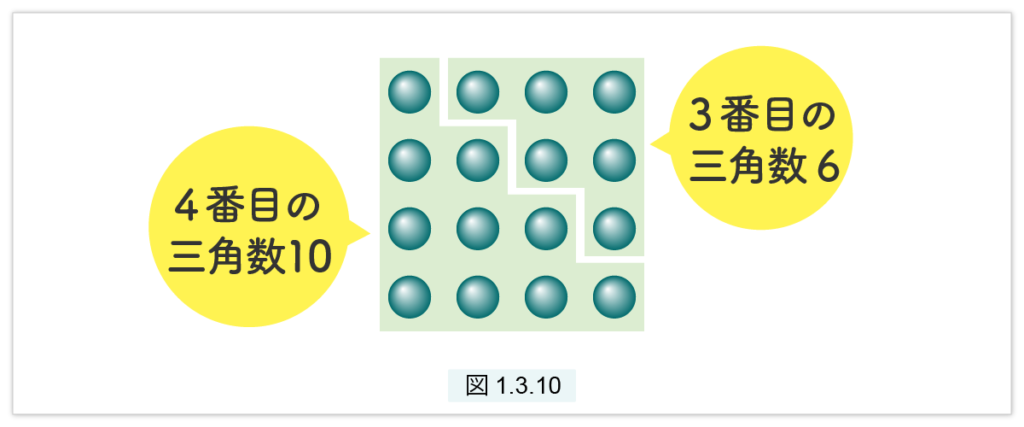
これを現代の式を使って表すと次のようになります。
n=5の時、すなわち5番目の四角錐数を計算すると次のようになります。

前節で示したように、「n番目の三角錐数×6 = n番目の準立方体」が成立します。したがって (2) が成立します。
四角錐の体積とピラミッドの体積
準立方体は「ほぼ立方体」である
前節で、準立方体は“ほぼ立方体”だと述べました。実際次が成立します。
(n – 1)番目の準立方体 < n番目の立方体 < n番目の準立方体
これを現代の式で書くと次のようになります。
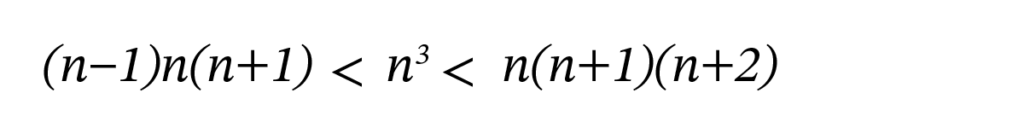
四角錐の体積の公式
数学では、正確な計算も必要ですが、反対におおざっぱに見ることも大切です。(2) をおおざっぱに見ると、「四角錐6個は、ほぼ立方体2個」とみなせますから、「四角錐は、ほぼ立方体の 3 分の1」とみなせます。
1辺が A の正方形を底面とし、高さがH の四角錐の体積 V は次で表されます。

古代エジプト人はこの「四角錐の体積の公式」を知っていました。古代エジプト人がどのようにしてこの公式を導いたのかは分かっていません。エジプト人は何万個もの石を積み上げ巨大なピラミッドを建造しました。積み上げた石の個数からここで述べたような方法で公式を得たのかもしれません。
以下でこれを証明しましょう。現代数学で証明しますが、基本的にはアルキメデスがよく用いた方法と同じです。
【四角錐の体積の公式】の証明
図1.4.2 のような四角錐を考えます。
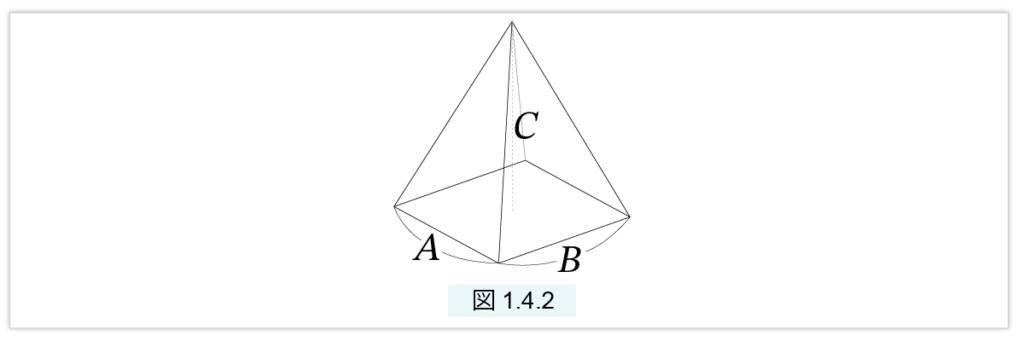
底面は A×B の長方形、高さは C とします。この四角錐を V とします。V は立体を示すとともに、その体積も示します。
自然数 n を適当に定め
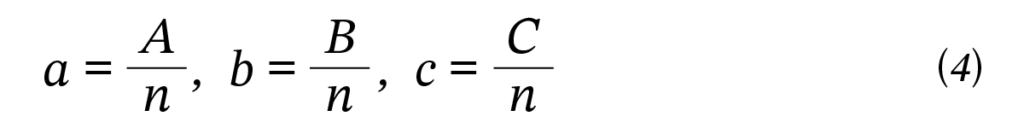
と置きます。a×b×c の直方体のブロックを積んで、ピラミッドを作ります。一番下は n×n 個、その上には (n – 1)×(n – 1) 個、…、最後に1個のブロックを載せます。ブロックの総数は
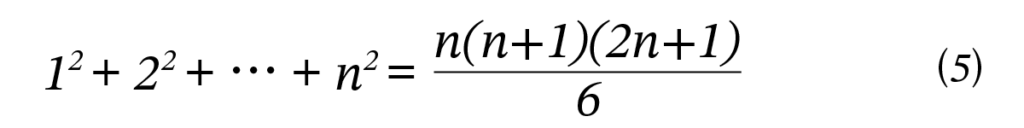
となります。このブロックを積んだピラミッドを Vn で表すことにします。図1.4.3が示すように、Vn は 図1.4.2 の四角錐 V をすっぽりと覆います。Vn から一番下の n×n のブロックを取り除いたピラミッドを Vn-1 とします。図1.4.4 が示すように、V は Vn-1 をすっぽりと覆います。
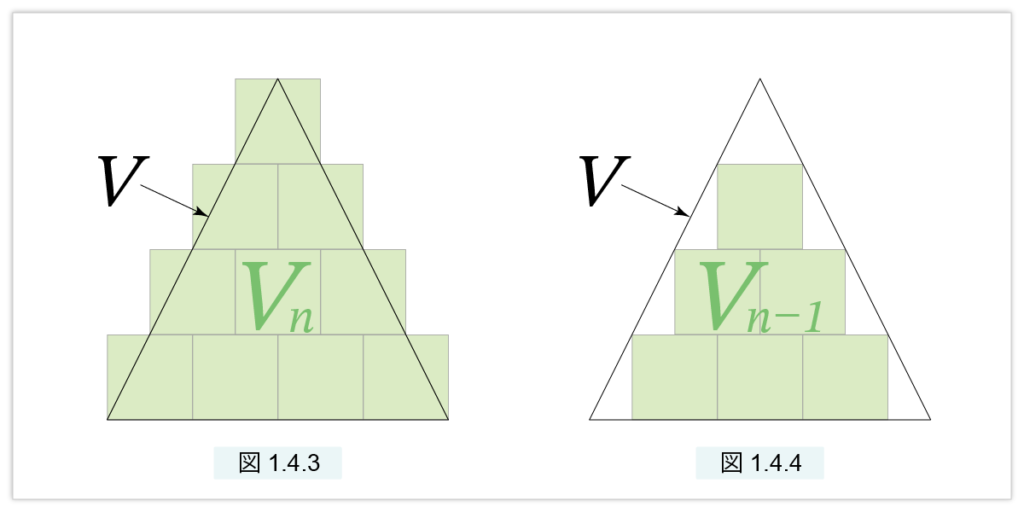
したがって、次が成立します。

Vn を計算しましょう。Vn は体積 abc のブロックを (5) で示される個数だけ積んだものですから
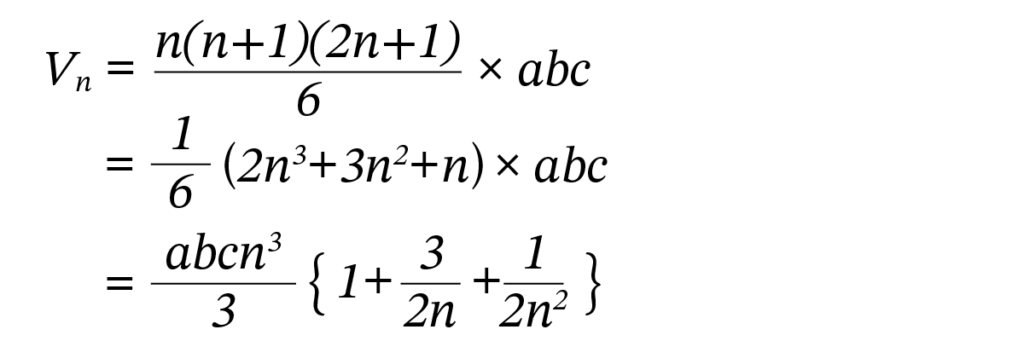
となります。したがって (4)より
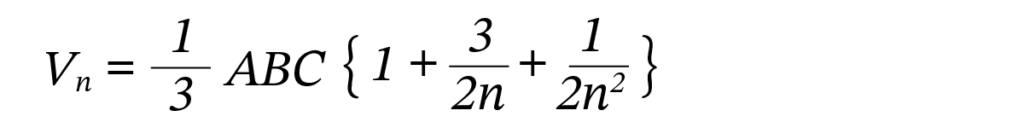
同様にして次が成り立ちます。
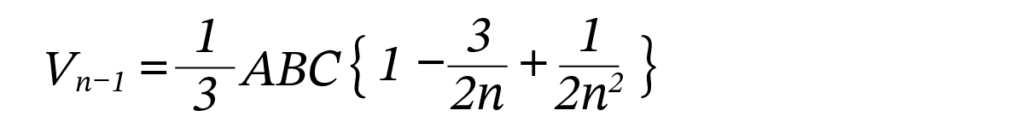
n が十分大きいと、3/2n と 1/2n2 は無視できます。したがって (6) より

が成立します。つまり、四角錐は外接する直方体の 1/3 となります。
面積の求め方
三角形の面積
自然数の列の n項までを棒グラフで表してみましょう。自然数の列は以下です。
1, 2, 3, …, n
図1.4.5 は n=10 の場合です。
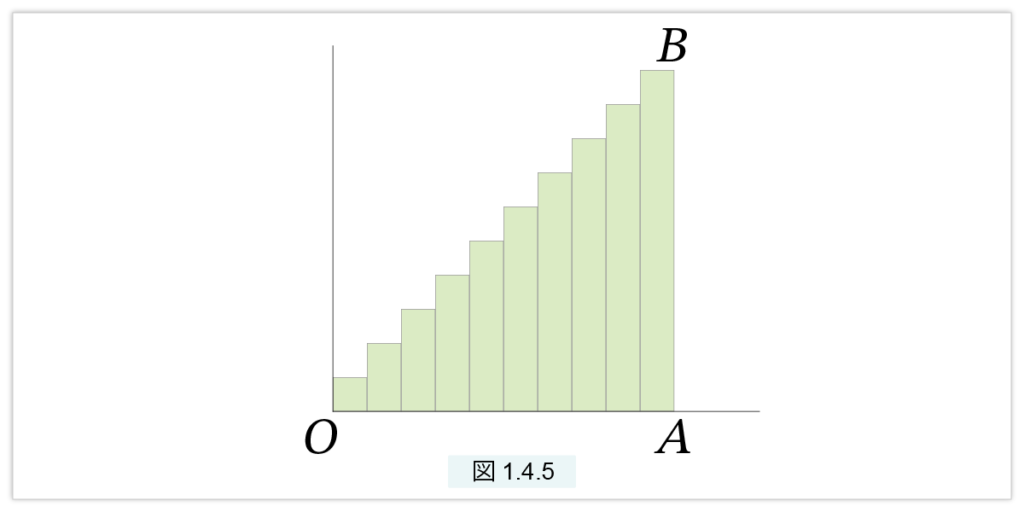
1+2+…+n は棒の和で、これはほぼ三角形 OAB の面積とみなすことができます。つまり、
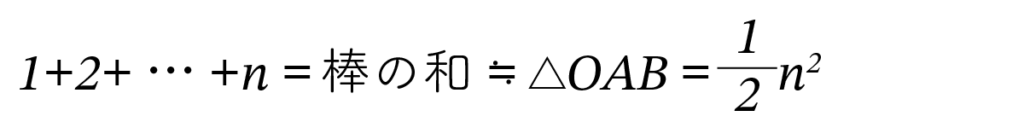
となります。
放物線下の面積
次に平方数の列を考えましょう。
12, 22, 32, …, n2,
これを棒グラフにしたのが図1.4.6 です。棒の上辺の中点を結んでできる曲線が放物線です。
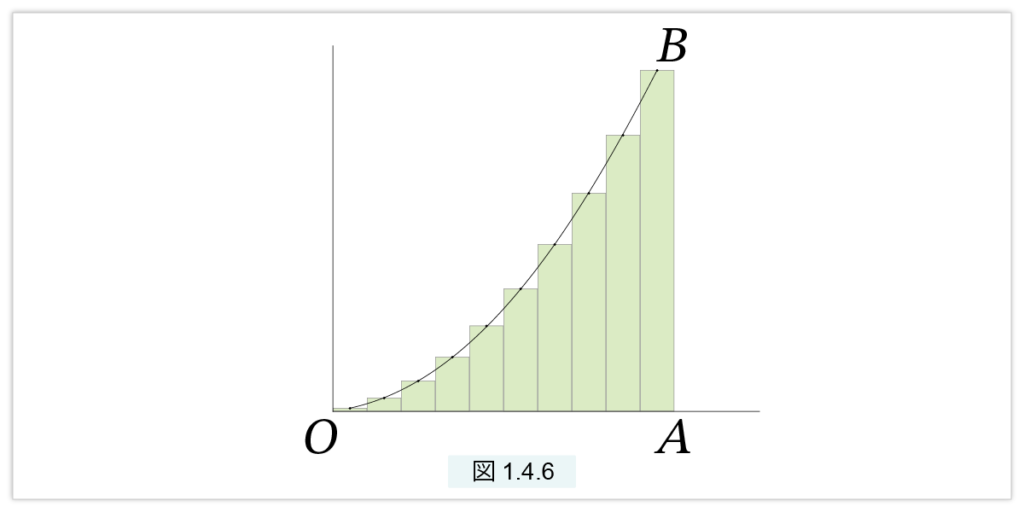
この場合も、和 12+22+ …+n2 は棒の和で、これはほぼ「放物線下の面積」、つまり放物線と線分 OA と AB で囲まれた面積となります。すなわち、

となります。
面積は線の集まりである
放物線の場合も三角形の場合も、n が小さいと誤差がありますが、n が大きくなると誤差は無視できるほどになります。ここで、線分 OA を固定しましょう。n を大きくするということは、OA をさらに細分するということです。すると、棒はどんどん細くなり線となります。つまり、面は“細い”線の集まりになります。
ギリシア人は「平方数は面」と考えていました。細い線を集めると面になるように、薄い面を集めると立体になります。上のピラミッドの体積の計算はこれを利用しました。この事実は、現在の3次元プリンター(3Dプリンター)や、薄い板を張り合わせて作る木工細工などからも想像がつくものと思われます。
まとめ
アルキメデスと数学の歴史
以上が、これからの議論の“予告編”です。現在の私たちは「放物線下の面積」をいとも簡単に計算できます。アルキメデスは同様の問題を込み入った議論を駆使して苦労して求めています。同じ問題をさまざまな方法で何度も解いています。まさに天才ともいえる巧妙で独創的なアイディアが用いられています。現在とどこが違うのでしょうか。そこには数学の発展というものがあるのだと思います。
現在の私たちが持っている“数”という概念を得るのに、人類は途方もない時間と努力を費やしてきました。皆さんは、“長さ”とか“面積”とか“体積”など、小学生でも知っている簡単な概念だと思っていると思います。しかし、これにも“数”と同様に多くの歴史があるのです。
PICK UP!!こちらのWeb連載もおすすめです

積分の源流、アルキメデスの求積
アルキメデスの結果は、やがてニュートンやライプニッツの“積分”へと発展します。ニュートンやライプニッツの難解で当時の最先端の理論も、いまや高校生の受験問題です。アルキメデスが扱った問題は、具体的で直感的に理解できる図形や立体が対象でしたが、解くのに多くのアイディアを必要としました。現在では、適用範囲が大きく広がりましたが、そのぶん理論が抽象的となりました。また、理論と技術を習得しさえすれば、誰でもがみな同じ方法で解けるようになりました。また、解くのに独創的なアイディアも必要なくなりました。
次の章ではアルキメデスの時代の人々が面積や体積をどのように扱っていたのかを詳しく見てみましょう。

