1-3. 三角数・正方形数・立方体数とは？古代ギリシアの数の分類を解説

現代数学は、抽象的で、形式的で無味乾燥だと感じている人が多いかもしれません。古代の数学もこんな風だったのでしょうか。ギリシア数学には「小石の数理」と呼ばれるものがあり、これは数学の原初の姿をとどめており、とても具体的で直観的です。

古代では小石を使って数を数えていた

calculate の語源

古代の人は数を数えたり計算したりするときに小石を使ったようです。これは「計算する」という意味の英語 calculate が小石を意味するラテン語 calculus から来ていることからの推定です。一方中国では細い竹を使って数を表していました。これは“算数”の“算”には“竹”が入っていることからも分かります。古代では、“数”といえば小石や竹の個数を表す自然数でした。まず自然数から始めましょう。古代の小石を使った数理と現代数学の数式を使った数学の違いを観察してください。

数え上げ〜数の習得

皆さんは自然数というと、幼稚園児でも知っている簡単なものだ、と思うかもしれません。しかし自然数はとても抽象的な概念なのです。

ではなぜ幼稚園児はいとも簡単に自然数を習得するのでしょうか。幼児教育の専門家は、それは「数えあげ(counting)」にあるといいます。子供のころ、お父さんかお母さんからお風呂などで繰り返し「ひとつ、ふたつ、みっつ、…」と数を数えるのを教わった人も多いと思います。数学は「頭の中だけで考える」ことも重要ですが、繰り返し練習して習得する「技術」も必要です。「数えあげ」を繰り返すことによって、子供たちは数という抽象的な存在をあたかも実在する対象として認識できるようになると考えられています。

「数える」とは何か

どんな動物も、哺乳類だけでなく、鳥も魚も、小さい数の識別はできるようです。これは生まれながらに持つ生得的な能力ですが、せいぜい3とか4といった小さい数に限るようです。数えるという行為は、数える対象と、“ことば”あるいは“ゆび”あるいは“小石”との対応をつけることです。

古代ギリシアにおける数の分類

三角数・三角錐数

前節〔1-2.数を並べる「数列」の概念〕では三角数とか三角錐数を定義しましたが、古代の人々はこれらをどのように扱っていたのでしょうか。小石を使って想像してみましょう。まず、原始列は小石を順番に並べます。(図1.3.1)

自然数の列は、まず1個置き、次からは直前のものに1個ずつ加えていきます。(図1.3.2)

次の三角数の列は、直前に作ったものを上に載せます。まず1個。次は2個の上に1個載せます。次は3個の上に今つくった“三角”を乗せます。さらにこれを続けます。(図1.3.3)

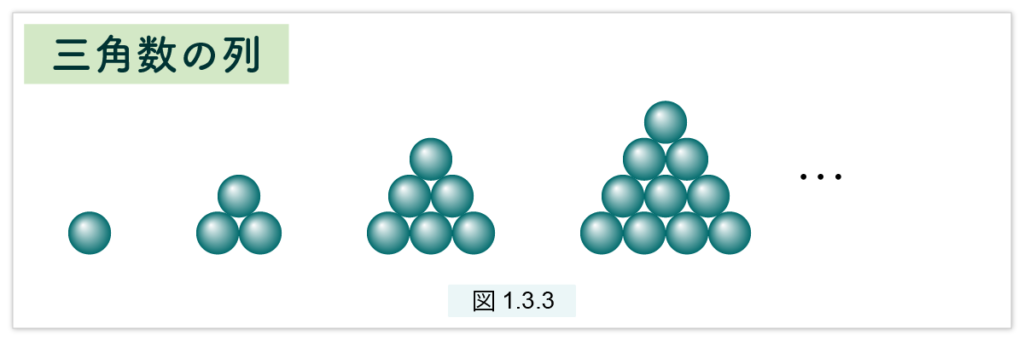
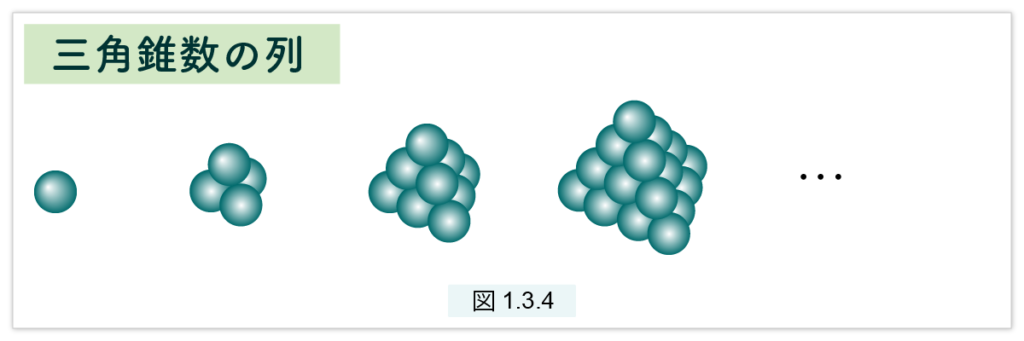
次の三角錐数は球状の“砲弾”を積んでいきます。図1.3.3 の 〇 は砲弾だと思ってください。 まず最初は1個の砲弾。次は図1.3.3 の3個の三角形の上に1個の砲弾を乗せると“三角錐”ができます。次は、図1.3.3 の三番目の三角形の上に、今つくった三角錐を乗せます。この手続きを繰り返します。(図1.3.4)

さて、これから次を証明したいと思います。

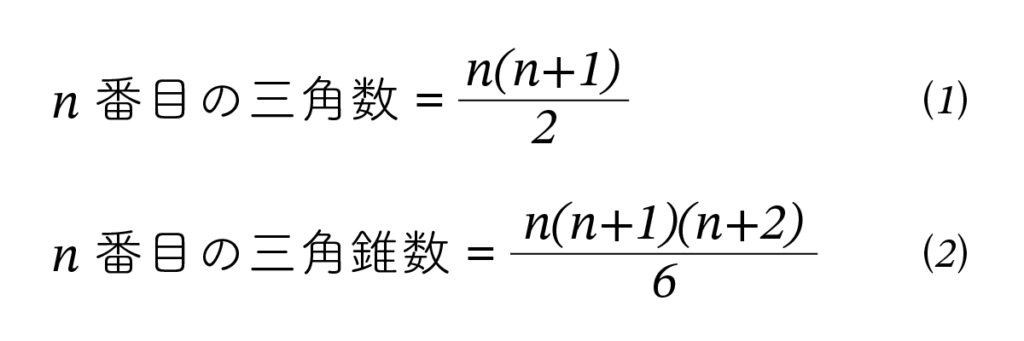
(1) と (2) では数式を使いましたが、古代では式など使えません。すべて言葉で表さなければなりません。これを証明のためにはまずいろいろな言葉を用意する必要がありました。

偶数と奇数

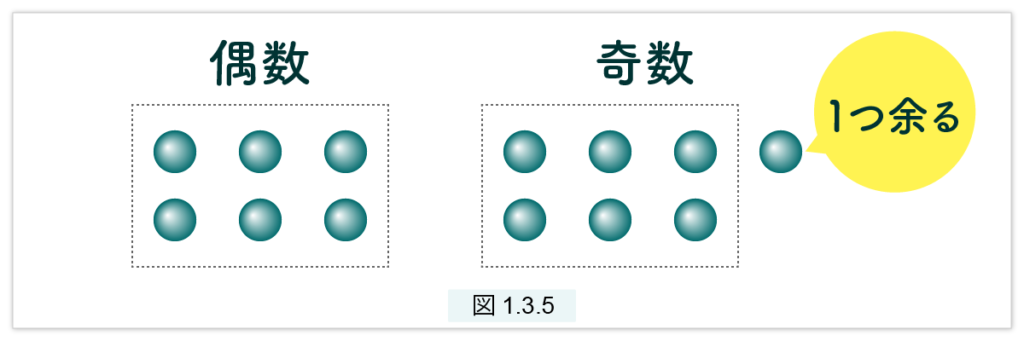
古代ギリシアでは数を「小石を並べてできる形」で分類しました。2列に並べることができる数を偶数、2列に並べると1つ余る数を奇数と呼びます。このように数を類別すること、つまり新しい言葉（概念）を作ることが「理論の始まり」です。(図1.3.5)

長方形数・正方形数・合成数

長方形に並べられる数を長方形数といいます。ただし1列は長方形とは認めません。正方形に並べることができる数を正方形数といいます。

ギリシアでは形で数を分類しましたが、現在の私たちは数を、掛け算を使って分類します。1以外の2つの数の積として表される数を合成数、ある数の平方（2乗）で表される数を平方数と呼んでいます。たとえば、ある数 a が2つの数 b と c の積で表されるなら、すなわち a＝b×c (b≠1, c≠1) なら、a は b と c から「合成される」から今では合成数と呼ばれ、ギリシア時代では、a個の小石は、縦 b、横 c の長方形に並べられるから長方形数と呼ばれたのです。正方形数と平方数の関係も同様で、同じ概念を表します。 長方形数でない数を素数といいます。また、3乗の形で表わされるもの、つまり a³ で表される数を立法数と言います。

以上をまとめると次のようになります。(図1.3.6)

三角数と準正方形数の関係

さて、(1) の証明をしましょう。図1.3.7(a) は4番目の三角数です。図1.3.7(b) はこれをひっくり返したものです。

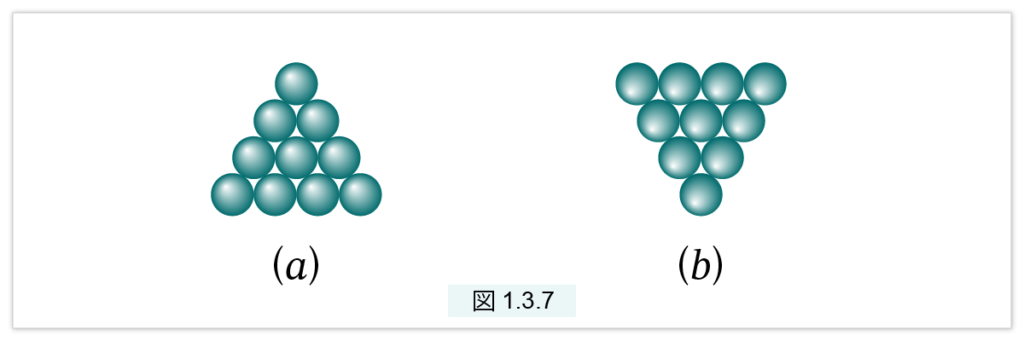
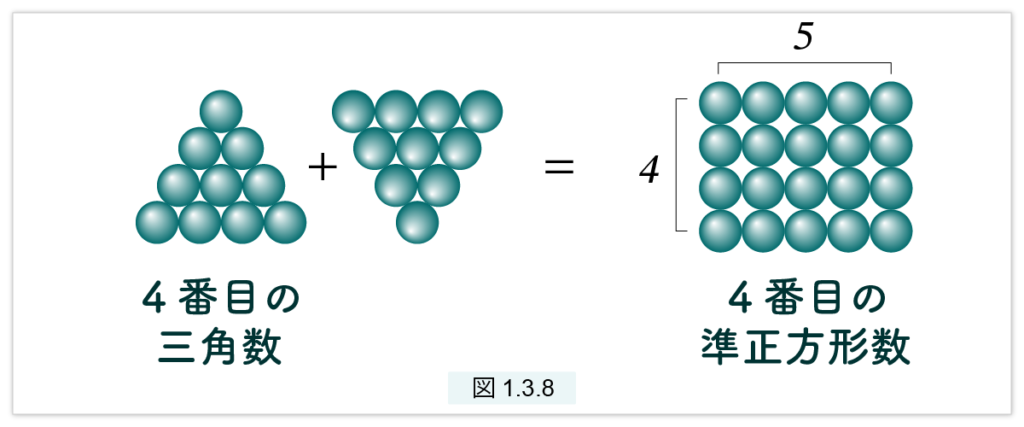
図(a) と図(b) を合わせると、4×5 の長方形になります。縦の個数より横の個数が1個だけ大きい長方形を準正方形と呼び、それの表す数を準正方形数とようことにします。特に縦の個数が n の場合、n番目の準正方形と呼びます。すると (1) は次のように表されます。

n番目の三角数は、n番目の準正方形数の半分である                     (3)

証明は、図1.3.8 から明らかです。

グノモン：ギリシア数学に現れるL字型

連続する奇数の和は平方数

前節で、1から始まる奇数列の和は平方数となると述べました。正確にいうと

1 + 3 + 5 + … + ( 2n – 1 ) = n²

となります。これに対しても図形による証明を与えておきましょう。奇数は図1.3.9 で示されるように、L字型の図形で表すことができます。図に現れる Ｌ字型、あるいはLを反転した図形はグノモンと呼ばれ、ギリシアの数学ではたびたび現れます。グノモンとは、日時計を簡略化したL字形の時計で、突起部の影の長さで時刻を測る器具です。

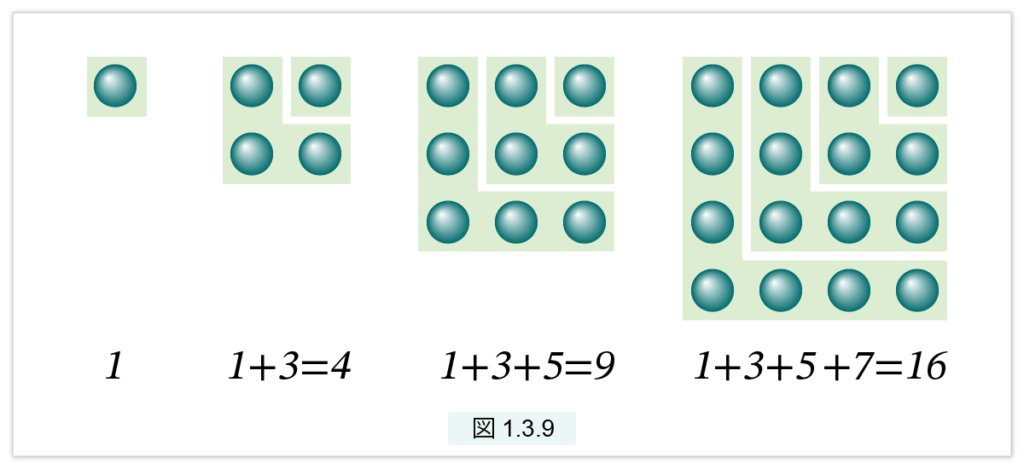
このように並べてみると、奇数の級数は正方形つまり平方数になっていることが一目瞭然でわかります。奇数の和が平方数になるなんて、不思議だとは思いませんか。

隣り合う三角数の和は平方数

平方数と三角数に関しては次も知られています。

隣り合う2つの三角数の和は平方数になる。                                  (4)

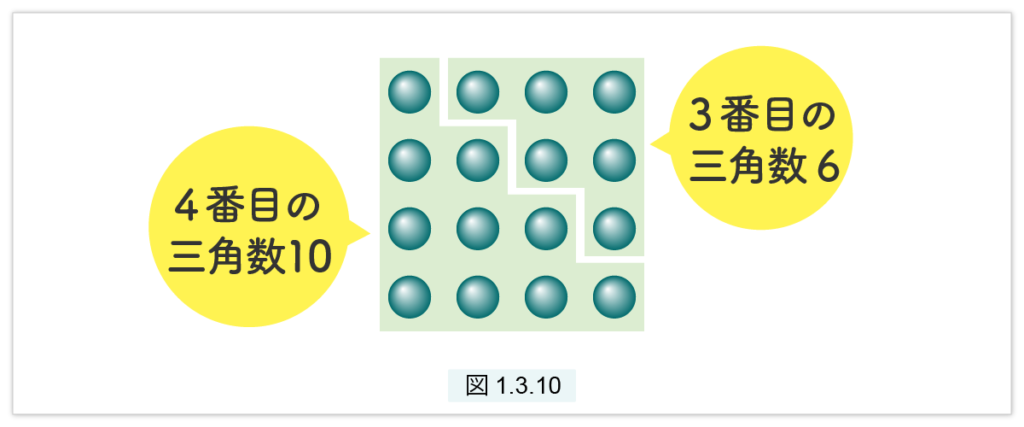
図1.3.10より、3番目の三角数 6 と4番目の三角数10を合わせると、平方数 4² ＝16 となることが分かります。(4) を n＝3 の場合について示しましたが、任意の n について成り立つことは明らかです。

三角錐数と準立方体数の関係

準立方体数とは

(2) の三角錐数を示しましょう。縦 n、横 n＋1、高さ n＋2 の直方体を準立方体、その表わす数を準立方体数と呼ぶことにします。すると、(2) は次のように表すことができます。

三角錐数は準立方体数の6分の1

したがって、

(三角錐数)× 6 ＝ 準立方体数                               (5)

となります。n が十分大きければ、準立方体はほぼ立方体となることに注意してください。

1番目の三角錐数

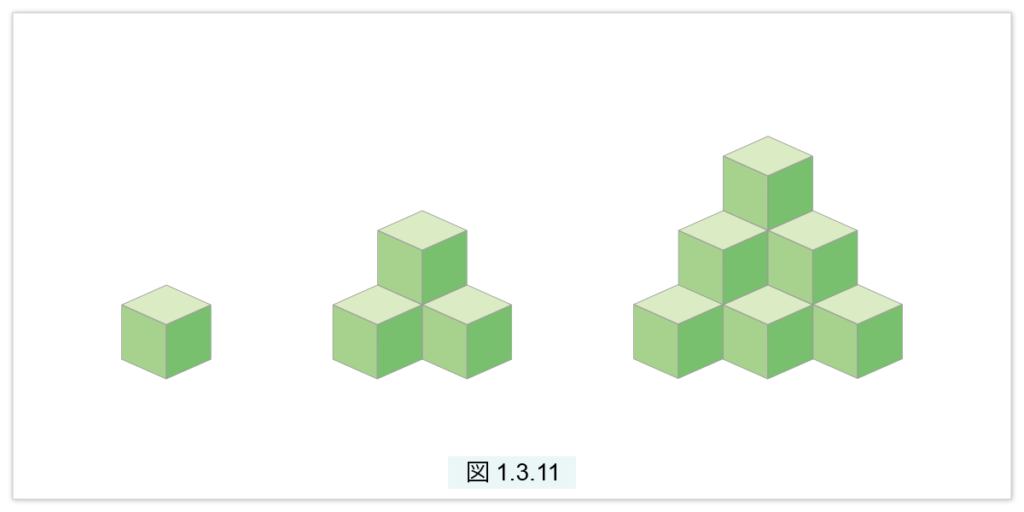
上の図1.3.4では砲弾（球）を積みましたが、今度はキューブ（小立方体）を積むことにします。図1.3.11 は最初の3つの三角錐数です。n＝1 の場合。1 は三角数でもあり三角錐数でもあります。一個のキューブが6個で 1×2×3 の準立方体ができます。

2番目の三角錐数

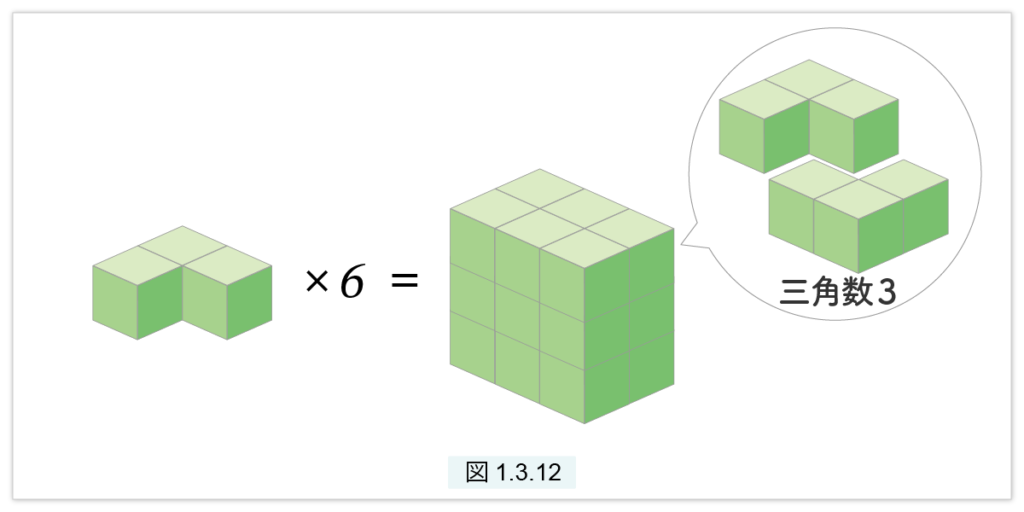
n=2の場合。2番目の三角錐数は、2つの三角数の和 1＋3 です。三角数 1は、6個で、n＝1 で作った 1×2×3 の準立方体とします。三角数 3 は 、2個で準正方形数2×3となります。すると、図1.3.12 が示すように6個で、2×3×3の直方体ができます。これと n＝1 で作った 2×3×1 と合わせると、2×3×4 の準立方体ができ上ります。同様の操作はいくらでも繰り返すことができます。

3番目の三角錐数

n＝3 の場合もやってみましょう。3番目の三角錐数は、3個の三角数の和 1＋3＋6 です。1＋3 に対しては今つくった準立方体 2×3×4 を使います。三角数 6 は、2個で 3×4 ですから、これを3個集めると、3×3×4 の直方体ができます。2つの直方体を合わせると、(2＋3)×3×4 となりますが、これは 3×4×5 の準立方体となります。