1-2. 数列とは何か？三角数・三角錐数を図でわかりやすく解説

数学用語はなぜ必要か

本連載では、アルキメデスの理論をなるべく誰にでも分かるように解説したいと思っています。数学が近づきがたいと思われるのは、数学が独特の言い回しをすること、特に“式”を多用することのようです。「数学は言語」だとよくいわれます。言語を習得するには、何度も何度も使ってみることです。古代の数学では式は現れません。言い回しも、おそらくは日常語とあまり変わらないものだったのでしょう。実は、すべて言葉で表すと、数学の表現がとても難解になるのです。数学独特の言い回しは、数学をできるだけわかりやすく表現しようと発達してきたのです。

本節で述べる用語は、とても基本的なことがらです。したがって、記号とか数学特有の言い回しをしなくても、平易な日常語で表せます。しかし、数学独特の言い回しを覚えてもらうために、あえて数学用語の説明をすることにしました。とっつきにくいかもしれませんが、一度覚えてしまうと、とても便利です。

もちろん古代には以下で述べるような用語や概念はありません。ここで述べるのは、現代数学の用語です。基本的な事項ですので、ご存知の方は読み飛ばしてください。また、必要になったら読む、ということでも結構です。

数列とは何か

数列の表し方

数学にとってもっとも基本的な概念の一つが数列です。数を一列に並べたものを数列といいます。たとえば次は奇数の列です。

1, 3, 5, 7, 9, 11, 13, …                                                (1)

次は2乗の形の数、つまり平方数の列です。

1, 4, 9, 16, 25, 36, …                                          (2)

数列を一般的に表すには、添(そ)え字(じ)付き変数を使って次のように表します

a₁, a₂, a₃, a₄, … , a_n, …                                            (3)

a₁, a₂, a₃…のどれかを表わすのにa_nといった記号を使います。記号 n は一般の自然数を代表する代名詞です。これらの添え字付き変数の使い方は、普通の変数と同じです。

(3)の数列を考えましょう。a₁ を第1項、a₂ を第2項 といい、n 番目の項 a_n を第n項といいます。特に最初の a₁ を初項といいます。(1) の数列の第n項は 2n – 1  で、(2) の数列の第 n 項は n² です。古代では 0 という数はありませんが、現代では数列の始めをゼロ 0 から始めたり、初項を a₀ としたりすることがあります。

級数：数列の和からなる数列

数列 (3) を使って、数列 b₁, b₂, b₃, … を次のように定めます。

b_n ＝ a₁ ＋ a₂ ＋ … ＋ a_n                                                (4)

数列 b₁, b₂, … を数列 a₁, a₂, …  の級数といいます。簡単にいうと、級数とは数列の和からなる数列のことです。

たとえば、数列 (1) の級数は

1, 1＋3, 1＋3＋5, 1＋3＋5＋7, …

ですから

1, 4, 9, 16, …

となり、(2) の平方数の列となります。つまり、「平方数の列は奇数の列の級数」となっています。不思議な現象です。古代ギリシアの数学者はこのような数の不思議に“神秘”を感じました。これについては次節で議論しましょう。

三角数と三角錐数

三角数とはどのような数列か

数列のなかでもっとも単純なのは次の(5)の数列です。

1, 1, 1, 1, 1, …                                                       (5)

この数列を原始列と呼ぶことにしましょう。原始列の級数は自然数の列となります。

1, 2, 3, 4, 5, …                                                       (6)

自然数の列 (6) の級数は次となります。

1, 3, 6, 10, 15, …                                              (7)

これらの数は図1.2.1 のように三角形に並べることができるので三角数と呼ばれています。

三角錐数とはどのような数列か

次は三角数の列の級数です。

1, 4, 10, 20, 35, …                                             (8)

この列に現れる数を三角錐数といいます。ここでおこなった操作は、このあといくらでも続けることができますが、ここでやめておきます。

配列と要素

得られた数列 (5)～(8) を次のように表にまとめましょう。

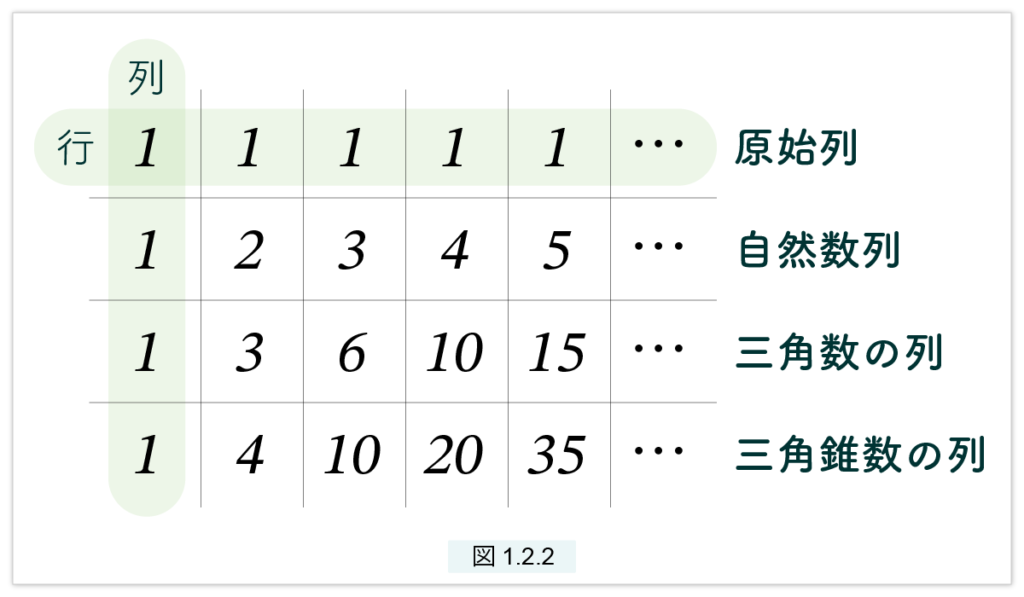
横を行といい、縦を列と呼びます。1行目は原始列、2行目は自然数列、3行目は三角数の列、4行目は三角錐数の列です。図1.2.2 に、たとえば F という名前を付け、i行i列の要素を F_ij で引用することにします。このような表現 F を配列といいます。配列は、行列とか表と呼ばれることもあります。また要素 F_ij は、F(i,j) と書かれることもあります（図1.2.3）。

図1.2.2 は次の規則に従って構成されます。

(a) F(1,j) ＝ 1, j＝1, 2, 3, …
(b) F(i,1) ＝ 1, i＝2, 3, …
(c) i＞1, j＞1 に対しては F_i,j ＝ F_i,j-1 + F_i-1,j

規則 (a) は1行目に関するもので、1行目が原始列 1, 1, 1, … であることを述べています。(b) は、i行目の1列が1であると述べています。

三角数と三角錐数の関係

(c)に関しては、現代数学ではこういった証明は数学的帰納法を使うのですが、ここでは一行ずつ見ていくことにします（図1.2.4）。

まず、2行目。2列目の 2 は左の1と上の１の和となっています。3列目の3は 1＋1＋1 ですが、これも左の2＝1＋1 と上の１の和となっています。3行目を見てみます。2列目の 3 は 1＋2 ですが、これも左と上の和となっています。3列目の６は 1＋2＋3 ですが、1＋2＝3 は左にきていますから、左と上の和となっています。これに続く列と、行についても同様に (c) が成立します。

規則 (c) を図示すると次のようになります。

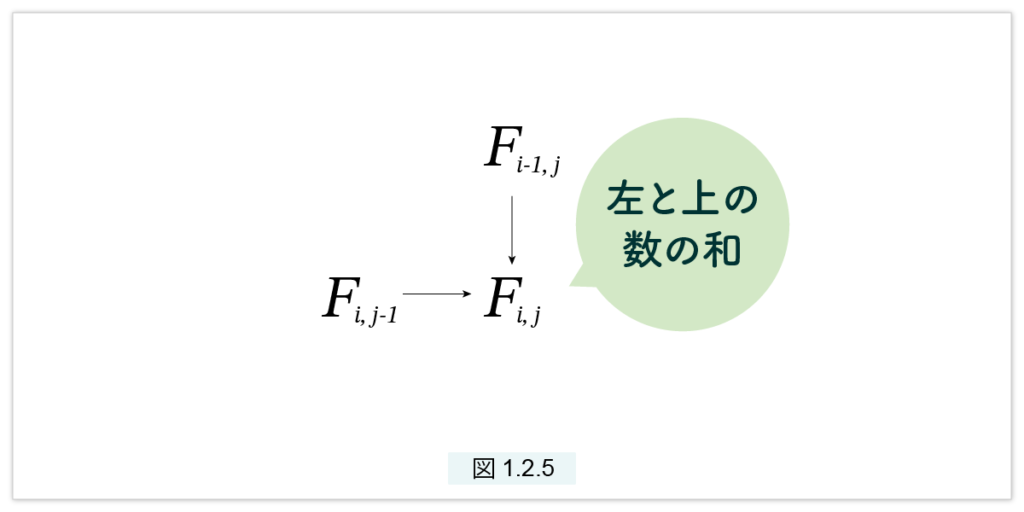
図1.2.5 は、F_ij  が左と上の和として表されることを示しています。

〔まとめ〕上で定義した次の数列を覚えておいてください。

       F_1,n: 原始列,  F_2,n: 自然数,   F_3,n: 三角数,   F_4,n: 三角錐数

これについては次が成立します。

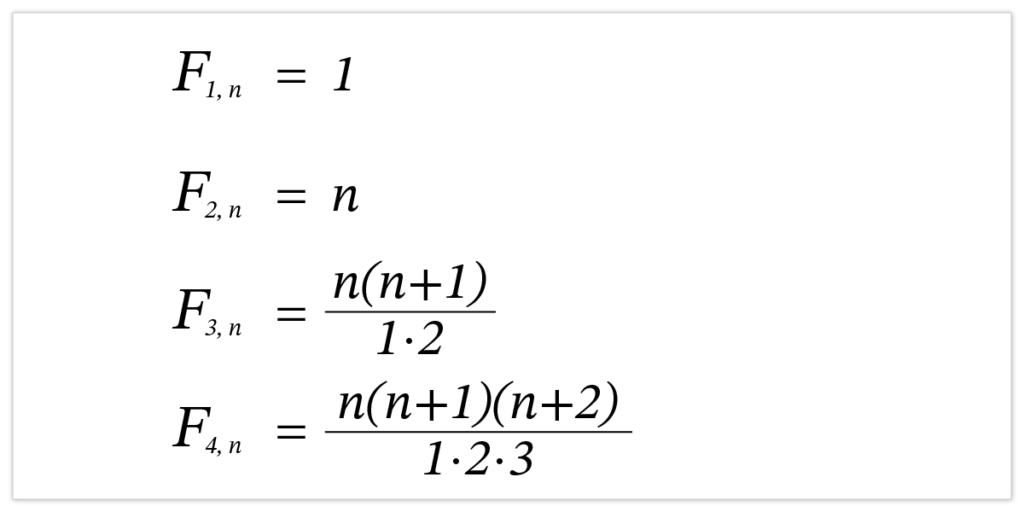
パスカルの三角形

パスカルの三角形の法則

図1.2.2を時計回りに45度回転させると、パスカルの三角形と呼ばれるものになります。

パスカルの三角形は本連載のメインテーマではありません。しかし数学では不思議なことに、まったく関係のないと思われるようなことが突然顔を出すことがよくあります。関係ないと思われても、頭の片隅に入れて置くと理解が深まることがあるので、ざっと目を通しておくことをお勧めします。

図1.2.6は図1.2.2 とまったく同じものなのですが、添え字の付け方が違います。_iC_j も C の i行 j列、あるいは C の第 ( i , j )要素などと呼ばれます。添え字が変わったので、上の規則 (a), (b), (c) も次のように変更します。

(a) _nC₀ = 1, n = 0,1,2, …
(b) _nC_n = 1, n = 0,1,2, …
(c) _nC_m = _n-1C_m-1 + _n-1C_m, n = 1,2, … , m = 1,2, … ,n-1

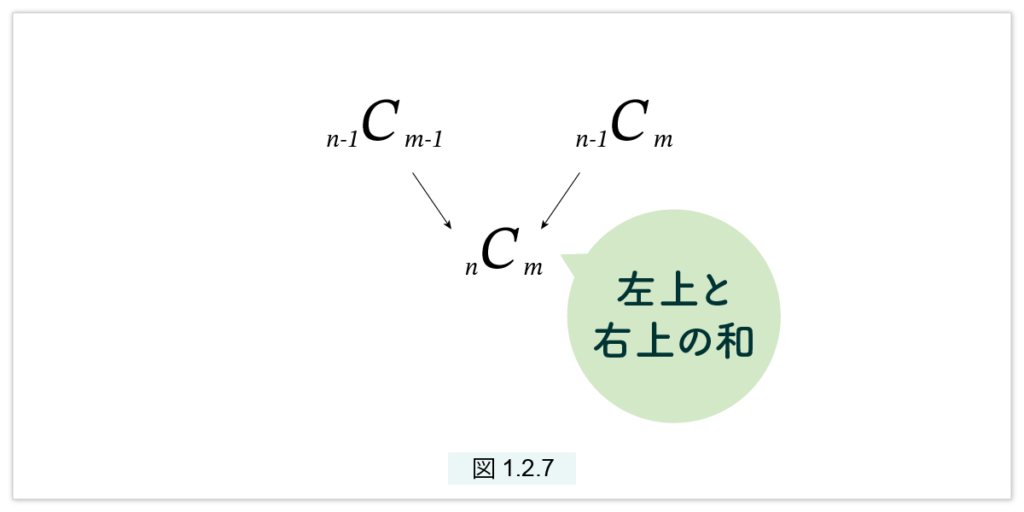
F の場合、図1.2.5 が示すように、「左と上の和」だったのですが、C の場合図1.2.7が示すように「左上と右上の和」となります。

パスカルの三角形と2項係数

図1.2.6に現れる数は、(a＋b)ⁿ の展開式の係数として現れるので、2項係数と呼ばれます。

( a + b )¹ = a + b
( a + b )² = a² + 2ab + b²
( a + b )³ = a³ + 3a²b + 3ab² + b³

(a＋b)ⁿ の展開式に現れる係数が上の (a), (b), (c) を満たすことは、次の展開式から想像できると思います。

( a + b )³ = ( a + b )² × ( a + b )
= ( a² + 2ab + b² )( a + b )
= a³ + 2a²b + a²b + ab² + 2ab² + b³
= a³ + ( 2 + 1 )a²b + ( 1 + 2 )ab² + b³

パスカルの三角形は、近世の数学においてとても重要な働きをします。このパスカルの三角形に代表されるように数学では非常に古い概念が現代においてもまったく色あせることなく使われているものが多いのです。

次回は、三角数や三角錐数を古代の人々がどのように扱っていたのかを詳しく見てみましょう。