小石の数理
- 1-1アルキメデスと無限
- 1-2数を並べる「数列」の概念
- 1-3小石の数理
- 1-4ピラミッドの体積
- 2-1数と量
- 2-2連続する正方形の和
- 2-3πの源流
- 2-4比の理論
- 2-5円周と円の和
- 2-6グノモンの定理
- 2-7比例中項
- 2-8量の列の和
アルキメデスの面積と体積
放物線の求積
2-7 比例中項
ページ目次
長方形の正方化
長方形の等積変換
線分で囲まれた図形を多角形といいます。多角形は図2.7.1で示されるように三角形に分解できます。
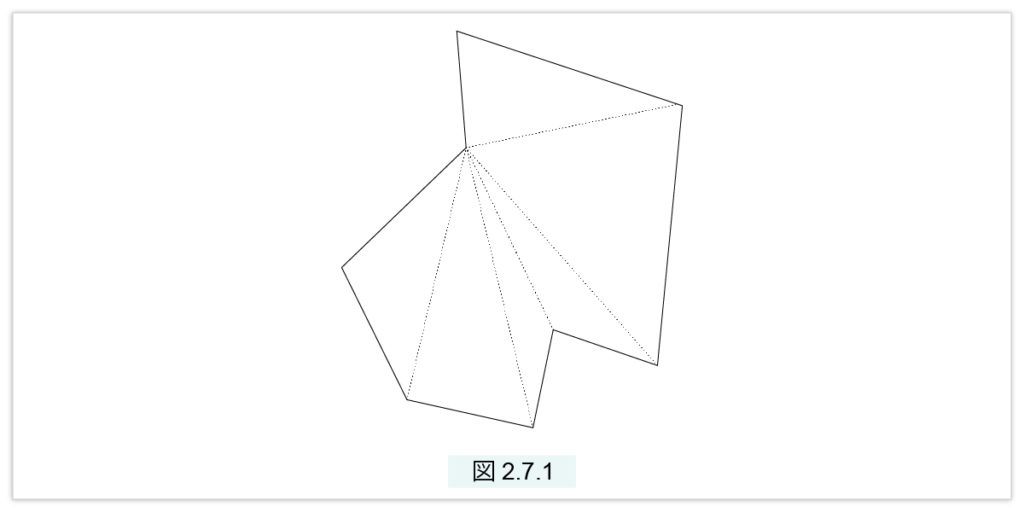
各三角形は前節〔2-6 グノモンの定理〕で述べたように長方形に等積変換できます。また、複数個の長方形の和は1つの長方形に等積変換できます。さらに次の定理が示すように、任意の長方形は正方形に等積変換できます。
比例中項
【定理】比例中項
任意の線分 a, b に対し次を満たす線分 x が作図できる
□(a, b) = □2(x)
図2.7.2 のように長さ a+b の線分 AB を H で分割し、AH=a, HB=b とします。AB を直径とする円を描き、H における AB の垂線と円との交点を C とします。
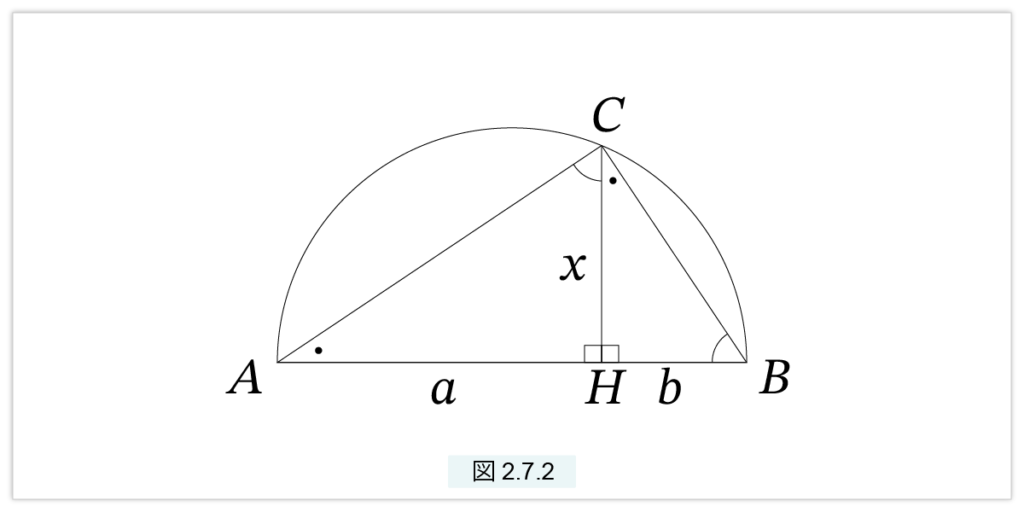
すると ∠C = ∠R となります。(∠R は“直角”と読みます) すると、
∠R = ∠A + ∠B = ∠A + ∠ACH = ∠B + ∠BCH
となります。よって
∠B = ∠ACH
∠A = ∠CHB
となりますから△AHC と △CHB は相似となり、
AH : CH = CH : HB
が成立します。HC = x と置くと
a : x = x : b
となります。〔内項外項〕の定理より、
□(a, b) = □2(x)
が得られます。
比例中項の公式
与えられた線分 a と b に対し、
a : x = x : b (1)
を満たす x を a と b の比例中項といい、記法
√ (a, b)
で表します。これは、式 (1) を満たす線分 x という意味であって、現代の \( \sqrt{ab} \) ではないことに注意してください。□2(x) が正方形を意味するものであって、現在の x2 ではないのと同様です。
次の公式は、以下の議論でたびたび用います。
【公式】比例中項
□(a, b) = □2(√ (a, b))
4つの長方形の間の面積比
2重比
次の定理は比 a : b を分数 a/b とみなした時の“積”にあたりますが、〔比の積〕という定理の名前は〔2-4 比の理論〕ですでに使っているので〔2重比〕という名前を付けました。
【定理】2重比
線分 a, b, c, d, x, y, u, v に対し次が成立する。
a : b = x : y, c : d = u : v なら □(a, c) : □(b, d) = □(x, u) : □(y, v)
直観的には、図2.7.3 に示すように「4つの長方形の間の面積の比」を考えれば、覚えやすいと思います。
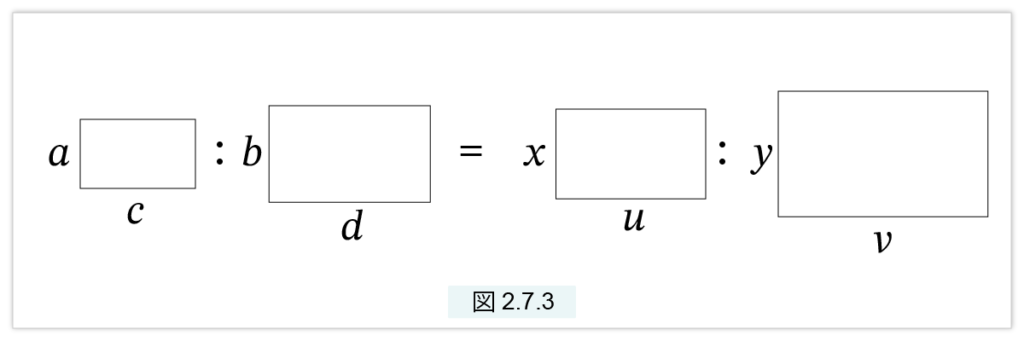
変数が8個も出てくるので、初めての皆さんは何を表しているのか意味が読み取れないかもしれません。現在の言葉で言いなおすと、これは次の式で表される「分数の掛け算」の規則を表しています。古代ではすでに分数の掛け算が行われていたのです。
\( \frac{a}{b} = \frac{x}{y} \) かつ \( \frac{c}{d} = \frac{u}{v} \) ならば\( \frac{a}{b} \times \frac{c}{d} = \frac{x}{y} \times \frac{u}{v} \)
〔2重比〕の定理の証明
〔2重比〕の定理 を証明しましょう。
a : b = □(a, c) : □(b, c)
x : y = □(x, u) : □(y, u)
∴ □(a, c) : □(b, c) = □(x, u) : □(y, u) (1)
c : d = □(b, c) : □(b, d)
u : v = □(y, u) : □(y, v)
∴ □(b, c) : □(b, d) = □(y, u) : □(y, v) (2)
(1) と (2) と命題〔比の積〕より、
□(a, c) : □(b, d) = □(x, u) : □(y, v)
比の2乗、相似面積比
次の2つの定理は、〔2重比〕の定理 からただちに得られます。
【定理】比の2乗
a, b, x, y 線分とする。
a : b = x : y なら □2(a) : □2(b) = □2(x) : □2(y)
【定理】相似面積比 – 面積比は辺の自乗比
△ABC と △XYZ が相似なら、△ABC : △XYZ = □2(BC) : □2(YZ)
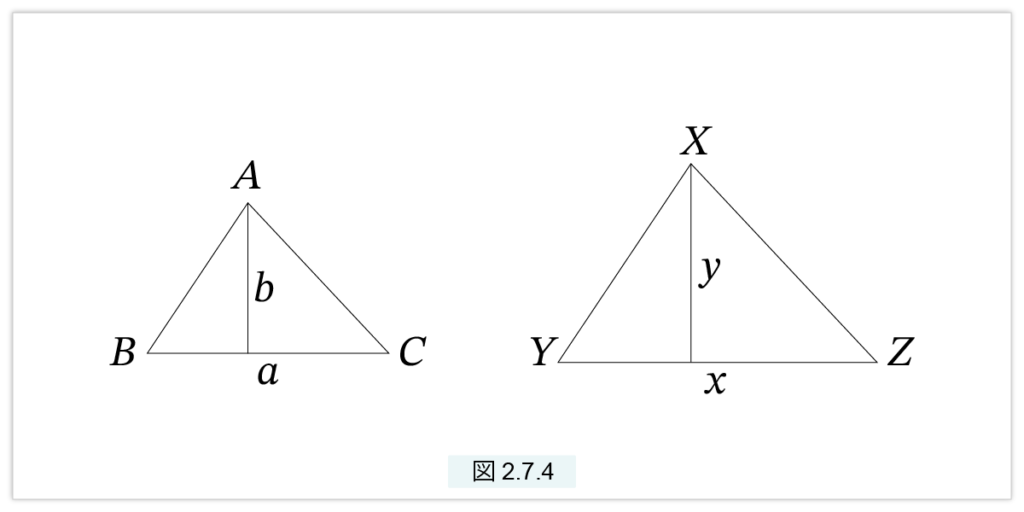
△ABC の高さを b、BC=a、△XYZ の高さを y、YX=x と置きます(図2.7.4)。すると、
△ABC = 1/2 □(a, b)、 △XYZ = 1/2 □(x, y)
よって、
△ABC : △XYZ =□(a,b) : □(x,y)
となります。△ABC と △XYZ は相似だから、 a : x = b : y となります。したがって、
a : x = a : x と b : y = a : x
に〔2重比〕の定理を適用すると、
□(a, b) : □(x, y) = □2(a) : □2(x)
が得られます。
比例中項が果たす重要な役割
アルキメデスの時代の掛け算
皆さんは2つの数 a と b の掛け算がどのように定められているか知っていますか。a と b が分数とか小数で表わされているなら、計算できますが、数には円周率 π とか √2 のような無理数があります。アルキメデスにとっては、数とは自然数だけですが、辺 a と b に関しては、a と b の積 a×b に対応するものとして、長方形 □(a, b) を考えました。つまり □(a, b) が現在の私たちの実数の掛け算 a×b に対応するのです。
正方化の意味
この節の最初に述べたように任意の多角形は三角形に分割されます(現在でも、任意の図形は多角形に分割し処理されます)。三角形は同じ面積の長方形に変換でき、複数の長方形は足し合わせることができます。また、長方形は同じ面積の正方形に変換できます。正方化する理由は、2つの正方形が等しいか、あるいはどちらが大きいかが判断できるからです。これには今回のテーマである “比例中項”という概念が用いられました。
a と b の比例中項を √ab と書きました。これは現代の“平方根”です。とくに 1 と a の比例中項は √a でし。アルキメデスは“平方根”に対応するものまで使っていたのです。
現在の私たちは a の2乗 a2 を a の平方(英語でsquare)といいますが、これは □2(a) という意味です。最後に述べた 相似面積比 の結果は、2つの相似な多角形の面積比は、対応する辺の自乗比となる、という結果です。
