小石の数理
- 1-1アルキメデスと無限
- 1-2数を並べる「数列」の概念
- 1-3小石の数理
- 1-4ピラミッドの体積
- 2-1数と量
- 2-2連続する正方形の和
- 2-3πの源流
- 2-4比の理論
- 2-5円周と円の和
- 2-6グノモンの定理
- 2-7比例中項
- 2-8量の列の和
アルキメデスの面積と体積
放物線の求積
2-5 円周と円の和
ページ目次
地球を一周するロープを1m持ち上げると?
前節〔2-4 比の理論〕で比の公式がいくつか出てきました。今回はこれらの公式がどのように使われるのかを見てみましょう。その前に皆さんに問題を出します。頭の体操だと思って考えてみてください。
地球の赤道をロープで結んだとします。地球は、表面がツルツルの完全な球だとします。ロープの長さは地球の周長の約4万キロメートルです。さて、このロープを1メートルだけ持ち上げるにはどのくらいの長さのロープが必要でしょうか。もちろん、ロープは伸び縮みしないものとします。
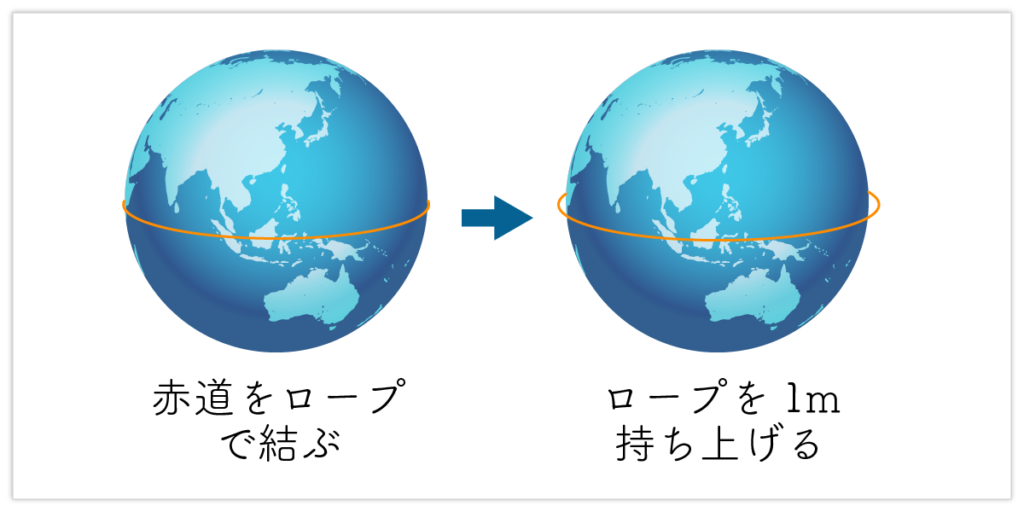
地球の周長は約4万キロメートルもあるので、ロープを1m持ち上げるには相当の長さを継ぎ足す必要があるような気もします。実際はどうなのでしょうか。
現在の皆さんは円周率πが使えますから円周は簡単に計算できます。地球の半径を r1メートルとすると、赤道の長さは 2πr1メートルになります。半径をr2(=1)メートル増やします。

すると、
2π(r1+r2) = 2πr1 + 2πr2 (1)
となります。つまり、地球を結んだロープを1メートル持ち上げるには、ロープを 2πr2 ≒ 6.3メートルだけ継ぎ足せばよいことになります。
--Advertising--
円周の足し算
古代では「円周の足し算」をどのように考えたか
(1) を古代の表現方法で表すと、
〇(r1+r2) = 〇(r1) + 〇(r2) (2)
となります。 〇(r1) は半径がr1の円の円周です。
アルキメデスは (2) をどのように証明したのでしょうか。
数学は、与えられた規則に従って行う団体競技や将棋などのゲームでと同じで、与えられた公理や規則以外のものは使うことはできません。使ってよいのは前節で述べた「比の規則」だけです。それでは (2) を証明しましょう。
〔円周率〕の定理より、
〇(r1) : 〇(r2) = r1 : r2 (3)
〇(r1+r2) : 〇(r2) = r1+r2 : r2 (4)
が成立します。次に定理〔比の和〕の特別な場合
A:B = a:b なら (A+B):B = (a+b):b
を (3) に適用すると、
〇(r1)+〇(r2) : 〇(r2) = r1+r2 : r2 (5)
が得られます。(4) と (5) より
〇(r1+r2) : 〇(r2) = 〇(r1)+〇(r2) : 〇(r2)
この比例式の右項は共に 〇(r2) です。したがって、命題〔右項の一致〕より (2) が得られます。
円と長方形の定理
現代では、円を考えるときは常に半径を基準として考えますが、古代では半径よりは直径、直径よりは円周を基準として考えました。たとえば木材を伐採するとき、木の円周は木を切り倒さなくても測ることができるからです。円周が分かれば、円の直径や半径は円周から計算できます。次は、「円は円周を底辺、半径を高さとする長方形の半分」であることを述べています。
【定理】 円と長方形
〇2(r) = 1/2 □(C, r)
円に内接する正n角形と外接正n角形を考えます。〔 2-3 πの源流 〕でおこなった議論より、
内接正n角形 < 〇2(r) < 外接正 n角形
が成立し、n が大きくなると、内接正 n 角形と外接正n角形は限りなく円に近づきます。図2.5.1 は内接正n角形と円を円の半径で切り、横に並べたものです。
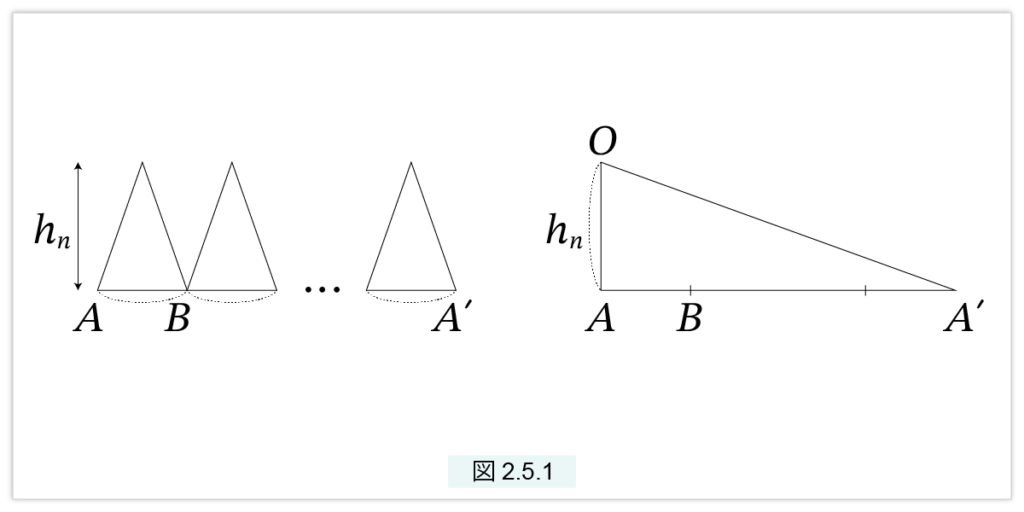
線分AA’は正n角形の外周で、n が大きくなると、円周 C に近づきます。hn は △AOB の高さで、n が大きくなると、円の半径 r に近づきます。並んだ n個の三角形は高さがみな hn なので、この n個の三角形の和は、右の図の直角三角形 OAA’ となります。つまり、
内接正n角形 = △OAA’
となります。内接正n角形は円に近づき、△OAA’ は底辺がC、高さが r の三角形に近づきます。
ギリシアの三大難問「円の正方化」
円の正方化とは
ギリシアの三大難問の一つに円の正方化というものがあります。これは、「与えられた半径 r の円に対し、コンパスと定規だけを使って、同じ面積の正方形を作図せよ」という問題です。定理〔円と長方形〕は、この問題を解いたことになりません。線分 r から円周 C が作図できないからです。これは論証数学であるギリシア幾何学を象徴する問題です。円周率πの値を 22/7=3.14257… と 0.1% 以内の誤差まで求めた実践科学者のアルキメデスにとって、円と実質的に同じ面積の正方形を実際的な方法で書いてみせることなど造作もないことだったでしょう。もちろん、ギリシア幾何学の伝統を守るアルキメデスは、これらのことは十分に承知していました。
円の面積と正方形の面積の関係
現在の私たちは半径 r の円の面積は πr2 と簡単に表せます。しかし古代では、記号πも、量の掛け算も使えません。〔円周率〕の定理 は、「円周は半径に比例する」というものでした。古代では「円の面積は半径の2乗に比例する」とは言えません。これを古代のいい方で述べると「円の面積は、半径を1辺とする正方形の面積に比例する」となります。正式には次のようになります。
【定理】円と正方形の面積比
〇2(r1): 〇2(r2) = □2(r1): □2(r2)
〔内項の交換〕を適用とすると、次になる
〇2(r1): □2(r1) = 〇2(r2): □2(r2)
「円と正方形の面積比」の証明
現代数学は“式の変形”で証明します。式の変形に慣れないと、なかなか難しいですが、ゆっくりと追えば自分でもコツがつかめるようになりますので、辛抱強く追いかけてください。
半径 ri の円の円周を Ci とする(i=1,2)。すると定理〔円と長方形〕より
〇2(r1) : 〇2(r2) = □(C1, r1) : □(C2, r2)
が得られます。〔2-4 比の理論〕で述べた 定理〔長方形の面積比〕より、
□(C1, r1) : □(r1, r1) = C1 : r1
□(C2, r2) : □(r2, r2) = C2 : r2
〔円周率〕の定理より
C1 : r1 = C2 : r2
よって次が成立します。
□(C1, r1) : □(r1, r1) = □(C2, r2) : □(r2, r2)
内項の交換によって、
□(C1, r1) : □(C2, r2) = □(r1, r1) : □(r2, r2)
= □2(r1) : □2(r2)
が得られます。以上をつなげると
〇2(r1): 〇2(r2) = □(C1, r1) : □(C2, r2) = □2(r1) : □2(r2)
が得られます。
--Advertising--
円の足し算
円の面積の和
上の定理で、円の面積比は、正方形の面積比となることが分かりました。2つの正方形の面積は、ピタゴラスの定理を使うと足すことができます。一辺がそれぞれ r1 と r2 の正方形の和は、底辺と高さが r1 と r2 の直角三角形の斜辺の長さを r3 とすると、
□2(r1)+□2(r2) = □2(r3) (6)
と表されます。
これを利用すると、半径がそれぞれ r1 と r2 の円の面積の和が
〇2(r1)+〇2(r2) = 〇2(r3) (7)
と表されることが分かります。
「円の面積の和」の証明
証明は円周の和 (2) のときとほとんど同じです。やり方さえ覚えれば誰でもできるようになりますから、以下の証明を見て練習してください。
定理〔円と正方形の面積比〕より、
〇2(r1): 〇2(r2) = □2(r1): □2(r2)
命題〔比の和〕を使うと、
〇2(r1)+〇2(r2) : 〇2(r2) = □2(r1)+□2(r2) : □2(r2)
となります。よって (6) より
〇2(r1)+〇2(r2) : 〇2(r2) = □2(r3) : □2(r2) (8)
が得られます。もう一度 定理〔円と正方形の面積比〕を使うと、
〇2(r3): 〇2(r2) = □2(r3): □2(r2) (9)
が得られます。(8) と (9) をまとめると
〇2(r1)+〇2(r2) : 〇2(r2) = 〇2(r3): 〇2(r2)
が得られます。両辺の右項が一致しますから、〔右項の一致〕より
〇2(r1)+〇2(r2) = 〇2(r3)
が得られました。
