2-4 比の理論

 

アルキメデスが創り上げた理論は、現在では解析学と呼ばれ、代数学に属します。代数学は“数”を扱うのに対し、アルキメデスが扱った対象は図形や立体などの幾何学的対象で“数”は現れません。代数学の土台となる“掛け算”や“割り算”の代わりにアルキメデスが用いたのは 比の理論でした。現代の私たちにとって、アルキメデスの理論を理解する上でいちばんの障害となっているのがこの比の理論です。近世に入り、量は数となり、比は分数となって、ギリシアの比の理論は代数学の中に吸収されてしまいました。現在では、アルキメデスの理論を比の理論を使わずに述べなおすことができます。しかしそれでは、アルキメデスの理論の真のすばらしさや、数学がどのように発展してきたかが分からなくなってしまいます。アルキメデスが扱った比の理論は、その後の数学の発展に大きく寄与したのです。これからその様子を見ていきましょう。 本サイトでは、ユークリッドの『原論』シリーズで〔比の理論〕を詳しく解説する予定です。ここでは、アルキメデスの理論を理解するのに必要な部分だけを簡単に紹介するのにとどめます。現在の皆さんは分数をよく知っていますから、

\( a : b\) とは \( \frac{a}{b} \)  のこと

と解釈すれば、これから述べる比の理論は理解できると思います。

2つの比が等しいとは

比の等価性

数学において最も重要な概念は、“等しい”という概念、つまり 等価性 の概念です。ユークリッドの『原論』においては、“比とは何か”についての説明はありません。比とは2つの量の間の“関係”であると述べ、あとは比の等価性の定義を形式的に述べるだけです。上で、比 a:b は分数 a/b のこと、と述べましたが、皆さんは、分数 a/b のちゃんとした定義を知っていますか。ケーキとかパイを分ける問題などで理解していると思います。しかしそのような具体的な例による説明は、分数の定義にはなっていないのです。例をいくら挙げても、“すべての分数”を尽くしているわけではないのですから。悪質な不動産屋みたいに、都合のいい例だけを見せているのかもしれません。

現代数学も『原論』と同じ方法を採っています。たとえば分数（有理数） a/b も、「これこれの規則を満たす2つの整数の組 (a, b) のこと」としか述べないのです。次に述べる比の等価性の定義は、後の数学で、分数（正確には有理数）の正式な定義に大きな影響を与えました。

2つの量 a と b が比を持つのは、a と b が同じ種類の量のときにかぎります。同じ種類の量に関しては足し算が許されます。したがって、量 a の自然数倍 na は許されます。以下では a:b と書いたときは、常に a と b は同じ種類の量とします。次は『原論』における比の等価性の定義です。

定義〔比の等価性〕
比a:b と c:d が等しいとは、任意の自然数 n と m について次のいずれかが成り立つことである。

(i) na＜mb ならば nc＜md
(ii) na＝mb ならば nc＝md
(iii) na＞mb ならば nc＞md

以下では、2つの比 a:b と c:d が等しいことを「a:b ＝ c:d」で表すことにします。もちろん古代ではこのような式も、2つの量 a と b の比を a:b と表すこともありません。古代では次のように表現しました。

「a:b ＝ c:d」 は 「a に対する b の比は、c に対する d の比に等しい」

天秤を使った直感的な説明

直観的な説明をしましょう。a, b, c, d を重さ（分銅）とします。図2.4.1 のような2つの天秤 A と B を考えます。天秤 A の左の皿には a を、右の皿には b を載せます。B の左には c を、右には d を載せます。A と B の左には同じ個数（n個）、右にも同じ個数（m個）を載せます。n と m をどのように選んでも2つの天秤が常に同じ振る舞いをするとき、比 a:b と c:d は等しいと定めたのです。

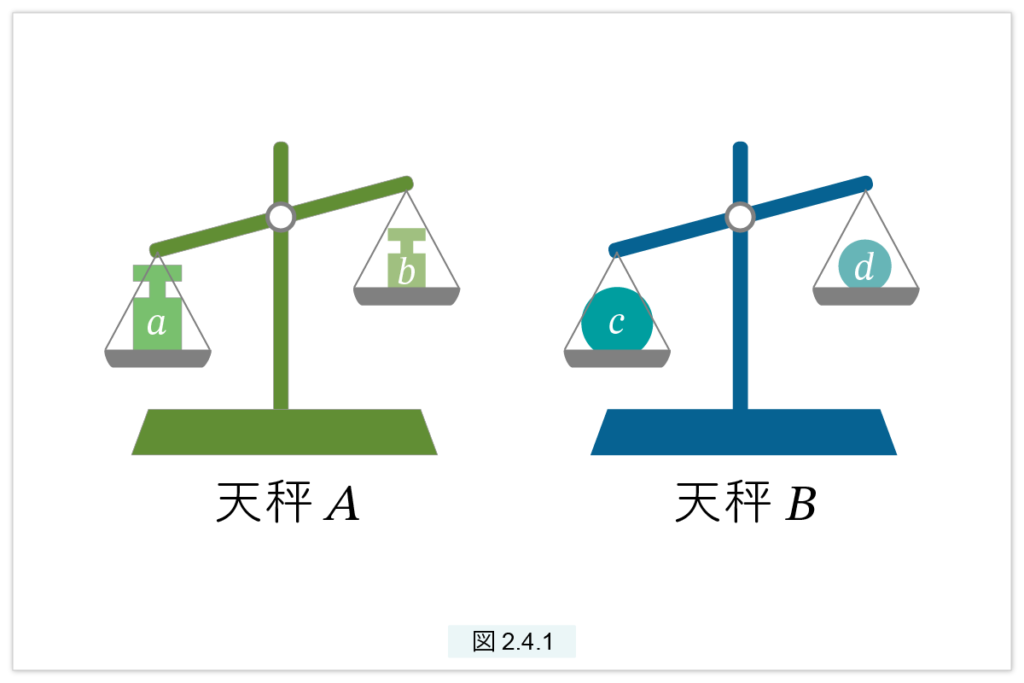
上では量を重さとしましたが、他の量の場合はその量を計る計測器とします。たとえば長さの場合は物差し、時間の場合は時計となります。a と b、c と d は同じ種類の量でなければなりませんが、a と c は違う種類の量でもかまいません。たとえば、a と b は長さ、c と d は面積でもかまいません。

比 a:b は分数と違って量とか数といった対象ではなく、2つの量の間の“関係”を表します。また、比に関する議論では、常に4つの量 a, b, c, d が現われ、「比 a:b が c:d と等しい」とか「比 a:b は c:d より大きい」といったことが議論されます。比の“大小関係”も、上の“等価性”のと同様に定義されます。皆さんは、分数の大小関係と同じで、

\(「a:b ＞ c:d」\) は \( \frac{a}{b} > \frac{c}{d} \) のこと

と理解してください。

比の等価性を使った証明

長方形の面積比

「数学は言語である」とよくいわれます。言語を習得するコツは何度も使ってみることです。上の定義を使って次の定理を証明しましょう。

〔2-3 πの源流〕で、「～は…に比例する」という表現がよく使われる、と述べました。この定理もそのうちの一つです。また、〔2-1 数と量〕では長方形の面積について議論ました。ここで少し復習をしておきましょう。□(c, a) は「底辺が c、高さが a 」の長方形を表します。底辺が等しい長方形は、重ねることによってどちら大きいか判定できます。すなわち次が成立します。

a ＞ b  なら □(c, a) ＞ □(c, b)                                (1)
a ＝ b  なら  □(c, a) ＝ □(c, b)                                (2)

また、na は線分 a をn個つなぐこと、n□(c, a) は長方形 □(c, a) を n個積むことですから次が成立します。

n□(c, a) ＝ □(c, na)                                           (3)

すると (1),(2),(3) より次が成立します。

(i) na＜mb ならば n□(c, a) ＜ m□(c, b)
(ii) na＝mb ならば n□(c, a) ＝ m□(c, b)
(iii) na＞mb ならば n□(c, a) ＞ m□(c, b)

したがって、定義よりa : b ＝ □(c, a) : □(c, b) が成立します。

ユークリッドの比の理論

4つの定理

以下で、ユークリッドの『原論』の比の理論を紹介します。証明は省略しますが、分数を知っている皆さんは、納得できると思います。またこれらの定理を使用するときは引用しますから覚える必要はありません。読み飛ばして、必要になったときに参照してもよいでしょう。

分数に書き換えると次のようになります。

内項の交換、内項外

比 A:B を考えるときは常に A と B は同じ種類の量でなければなりません。たとえば A が面積、B が長さであってはなりません。長さと面積は比較ができないからです。しかし、A:B ＝ a:b と書いた場合、A と B、a と b は同じ種類の量でなければなりませんが、A と a は必ずしも同じ種類でなくてもよいのです。

次の命題はよく用いますが、A, B, C, D が同じ種類の量のときに限ります。

現在の私たちは、長さ、面積、体積、… などはみな実数とみなしています。また、正の実数は線分の長さとして、数直線として考えています。したがって、面積、体積、角度、重さ、温度、時間、… などと、いろいろな種類の量を考えなくても、長さだけを考えればよいことになります。長さに関しては次が成立します。この定理の証明は〔2-6 比例中項〕で行います。

掛け算の定義とは

皆さんは実数 a と b の積 a×b の定義を知っていますか。近世に入ってヨーロッパに古代ギリシアの数学が伝わったとき、困ったのは数の積 a×b の定義でした。そのとき長さはすでに数となっていたのです。そこで a×b を「横a縦bの長方形の面積」と定義する人が現われ、古い著作ではこのように書かれています。しかしこれは、「面積とは何か」を明確に しなければ、掛け算の定義にはなりません。近世では、数（実数）の明確な定義もなく、したがって掛け算とか割り算の厳密定義もないまま、数学が議論されていたのです。

同じ種類の量 a と b が与えられたとき、どちらが大きいかは決まっています。しかしどちらが大きいかを実際に判定できるかどうかは分かりません。たとえば a と b が複雑な曲線の場合は、どちらが大きいか、あるいは等しいかが判定できないことがあるのです。a と b が同種の量、c と d が同種の量であっても、a:b と c:d が等しいのか、あるいは一方が他方より大きいのか判定ができないことがあります。上の「比の等価性」の定義は、「条件が満たされたとき、等価であると判断できる」という意味です。