2-2 連続する正方形の和

平方数の和の公式

現代の公式：2乗の和の公式とは

〔1-4 ピラミッドの体積〕では平方数の和（四角錐数）を考えましたが、これは数の和でした。アルキメデスは、これを面積の和に置き換えた、正方形の和を考えています。

平方数の和の現代の公式は

$1^2 + 2^2 + \cdots + n^2= \frac{n(n+1)(2n+1)}{6}$

となります。

アルキメデスが示したのは次の定理です。興味のある人は、これを現代の数式に変換して、上の式と同じになることを確認してみてください。

系 ：正方形の和

〔1-4 ピラミッドの体積〕の四角錐数の公式の証明も複雑でしたが、この定理の証明はそれ以上に長く複雑です。また、この定理は公式としては複雑で覚えにくいですが、実際には、次の系を用います。

系〔正方形の和〕　
線分 a と自然数 n＞1 に対して次が成立する。
(i) $3\{□^2(1a)＋□^2(2a)＋…＋□^2((n–1)a)＋□^2(na)\} ＞ (n＋1)□^2(na)$
(ii) $3\{□^2(1a)＋□^2(2a)＋ … ＋□^2((n–1)a)\} ＜ n□^2(na)$

(i) と (ii) の意味は分かりやすいと思います。(i) は、「一辺が a から na まで順次増加する正方形の和の3倍は、最後の正方形の n＋1 倍より大きい」と言葉で表せます。(ii) についても同様です。(i) は定理よりただちに得られます。

系(ii)の証明

定理の証明の前に、まず (ii) を証明しておきましょう。

式 (1) の左辺の □²(na) を右辺に移項すると

$3\{□^2(a)＋□^2(2a)＋ \cdots ＋□^2((n–1)a)\} \\ ＝ □(a, \{1＋2＋ \cdots ＋n\}a)＋ (n＋1)□^2(na) – 3□^2(na) \\ ＝ □(a, \{1＋2＋ \cdots ＋n\}a)＋ (n – 2)□^2(na) \\ ＝ □(a, \{1＋2＋ \cdots ＋(n–1)\}a)＋□(a, na) ＋ (n – 2)□^2(na)$

となります。ここで、前節〔2-1 数と量〕の〔正方形の3分割〕定理を適用します。

$＝ \frac{1}{2} \{□^2(na) – □(a, na)\} ＋□(a, na) ＋ (n – 2)□^2(na)$
$＝ \frac{1}{2} □^2(na) ＋ \frac{1}{2}□(a,na) ＋ (n – 2)□^2(na)$

 $a＜ na$ ですから

$＜ \left(\frac{1}{2} + \frac{1}{2} +n -2 \right) □^2(na) ＜ n□^2(na)$

が得られます。

「正方形の和」の式の証明

さて、問題の式 (1) を証明しましょう。アルキメデスはきわめて巧妙な方法をいくつも駆使しています。証明は長いですが、使われている手法はこれまでに述べたものだけですから、ゆっくり読めば分かるはずです。アルキメデスは n＝5 の場合を証明していますが、準一般的な証明です。

前節〔2-1 数と量〕で述べた 〔 正方形の3分割 〕の定理を使って □²(5a) から □²(1a) まで計算します。

$□^2(5a) ＝ □(a,5a) ＋ 2×□(a, (1＋2＋3＋4)a)$
$□^2(4a) ＝ □(a,4a) ＋ 2×□(a, (1＋2＋3)a)$
$□^2(3a) ＝ □(a,3a) ＋ 2×□(a, (1＋2)a)$
$□^2(2a) ＝ □(a,2a) ＋ 2×□(a, 1a)$
$□^2(1a) ＝ □(a,1a)$

これを辺々加えます。つまりこの5つの式の左辺は左辺で加え、右辺は右辺で加えます。すると、右辺に三角数の和、つまり三角錐数

$1＋(1＋2)＋(1＋2＋3)＋(1＋2＋3＋4)$

が現われます。この式に1は4個、2は3個、3は2個、4は1個現れますから、この式は

$＝ 1×4 ＋ 2×3 ＋ 3×2 ＋ 4×1 \qquad (2)$

と変形できます。したがって、上の式を辺々加えると、

$□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)＋□^2(5a)$
$＝ □(a, a＋2a＋3a＋4a＋5a)$
$＋ 2×□(a, 1×4a＋2×3a＋3×2a＋4×1a) \qquad (3)$

次に(2) の処理を考えます。アルキメデスは次の2つの公式を使いました。次で a と b は線分、n と m は自然数です。

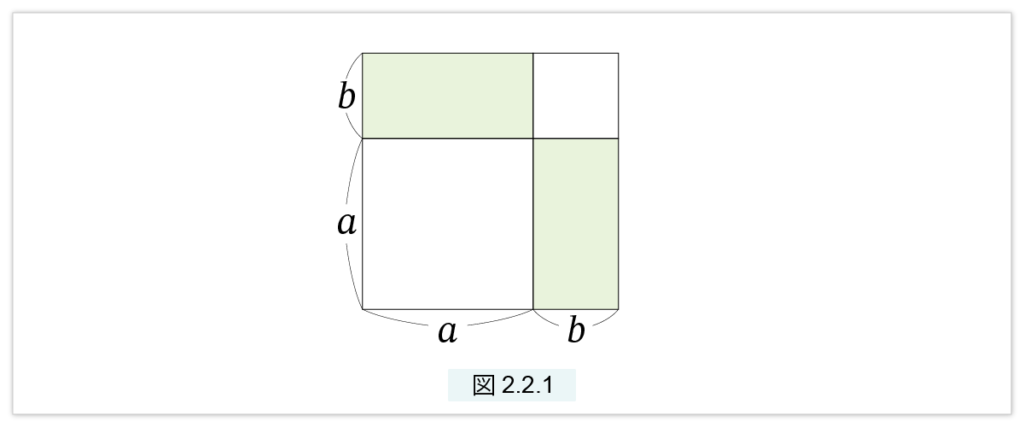
$(a)  □^2(a＋b) ＝ □^2(a) ＋ 2□(a,b) ＋□^2(b)$
$(b) □(na, mb) ＝ nm□(a, b) ＝ □(a, nmb)$

(a) は図2.2.1 より明らかです。

(a) を使うと□²(5a) は次のように展開できます。5a は目的の式 (1) の na にあたります。

$□^2(5a) ＝ □^2(1a＋4a) ＝ □^2(1a)＋□^2(4a)＋2□(a, 1×4a)$
$□^2(5a) ＝ □^2(2a＋3a) ＝ □^2(2a)＋□^2(3a)＋2□(a, 2×3a)$
$□^2(5a) ＝ □^2(3a＋2a) ＝ □^2(3a)＋□^2(2a)＋2□(a, 3×2a)$
$□^2(5a) ＝ □^2(4a＋1a) ＝ □^2(4a)＋□^2(1a)＋2□(a, 4×1a)$

辺々加えると

$4□^2(5a) ＝  2×\{□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)\}$
$＋2×□(a, 1×4a＋2×3a＋3×2a＋4×1a) \qquad (4)$

式 (4) から式 (3) を引きます。

$4□^2(5a) – \{□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)＋□^2(5a)\}$
$＝ 2×\{□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)\}$
$– □(a, 1a＋2a＋3a＋4a＋5a)$

整理すると

$4□^2(5a) ＋ □(a, a＋2a＋3a＋4a＋5a)$
$＝ 3×\{□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)＋□^2(5a)\} – 2×□^2(5a)$

よって、

$3×\{□^2(1a)＋□^2(2a)＋□^2(3a)＋□^2(4a)＋□^2(5a)\}$
$＝ 6□^2(5a) ＋ □(a, 1a＋2a＋3a＋4a＋5a)$

となります。準一般的な証明なので、5はnを、 6はn＋1 を表します。したがって、定理が証明されました。

放物線下の面積

数学にはよくあることですが、定理や補助定理がどのような意図考えられ、今後どのような使われ方をされるのか、途中では分からないことがよくあります。上の定理が使われるまで、しばらく別の話題に入りますから、この定理を現在の数学の言葉で説明します。現在の概念で過去の数学を語ることはよくないことなのですが、本連載の目的は過去の数学を通して、初心者に数学というものを知ってもらうことなので、ここはおきてを破ります。定理〔正方形の和〕の系は、次のように表されます。

(i) $3\{(1a)^2＋(2a)^2＋\cdots ＋ (na)^2\} > (n+1)(na)^2$
(ii) $3\{(1a)^2＋(2a)^2＋\cdots ＋ ((n-1)a))^2\} < n(na)^2$

長さ a を実数とみなし、na ＝ A と置きます。y ＝ x² のグラフを考えます。A を n 等分し

$x_1 = 1a, \quad x_2 = 2a, \cdots, \quad x_n = na,$
$y_1 = x_1^2, \quad y_2= x_2^2, \cdots , y_n = x_n^2,$

と置きます。図2.2.2(a) の棒グラフを考えます。

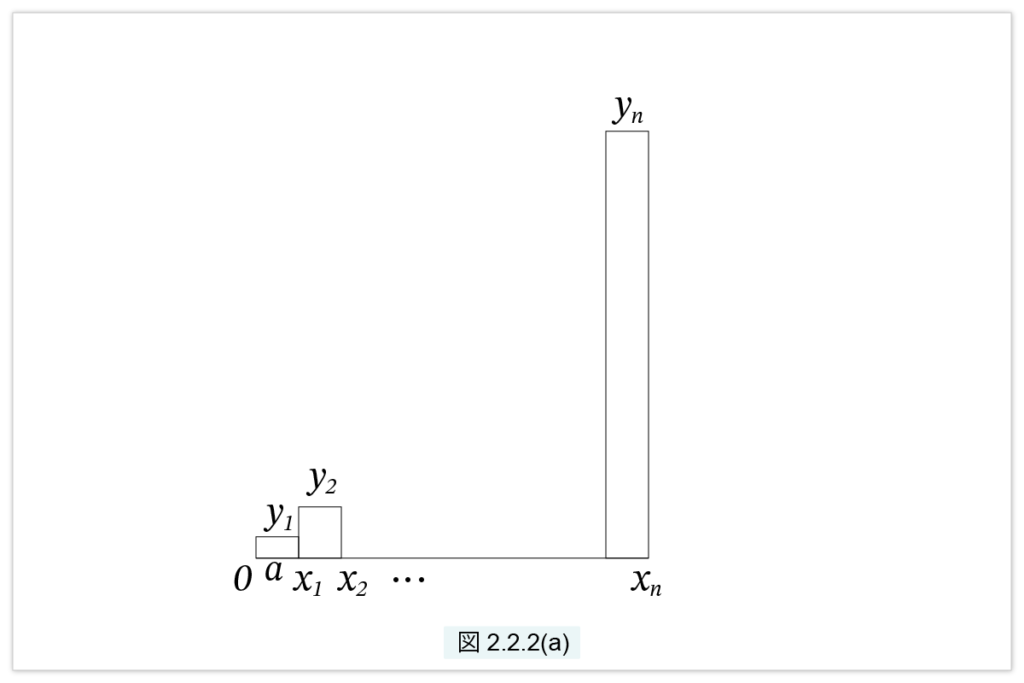
棒は、底辺が a で、高さが y₁, y₂, …, y_n ですから、棒の面積の和は

$ay_1+ay_2+… + ay_n= a\{(1a)^2+ (2a)^2 +…+(na)^2\}$

となり、上の (i) を用いると、

$> \frac{1}{3} a(n+1)(na)^2 > \frac{1}{3}(na)^3 = \frac{1}{3}A^3$

が成立します。

同様に、図2.2.2(b)の棒の面積の和は　

$ay_1 + ay_2 + … + ay_{n-1}= a\{(1a)^2 + (2a)^2 + … +((n-1)a)^2 \}$
$< \frac{1}{3} an(na)^2 = \frac{1}{3}A^3$

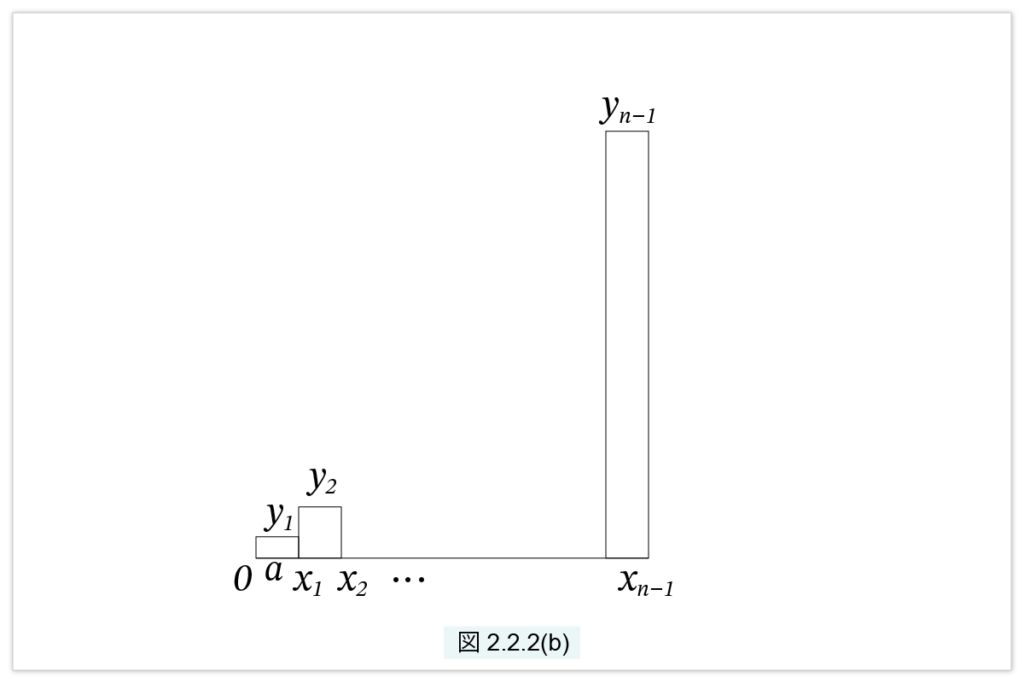
よって、両式をまとめると

$ay_1 + ay_2 + … + ay_{n-1} < \frac{1}{3} A^3 < ay_1 + ay_2 + … + ay_n$

が得られます。

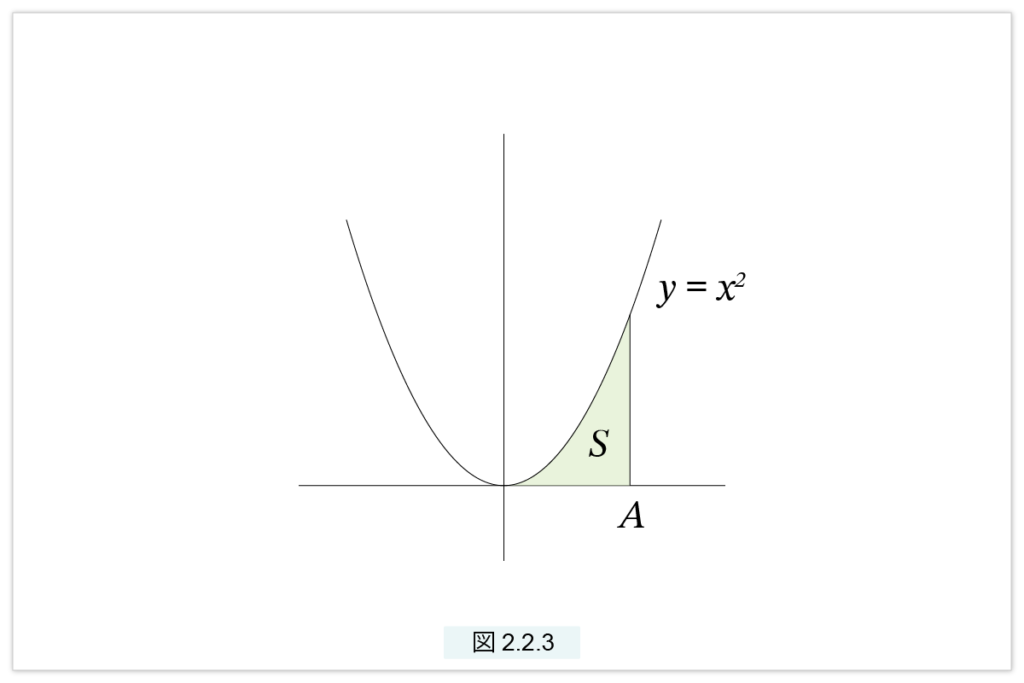
また放物線 y ＝ x² と x軸と直線 x＝A で囲まれた部分の面積を S と置くと(図2.2.3)

$ay_1 + ay_2 + … + ay_{n-1}< S < ay_1 + ay_2 + … + ay_n$

が得られます。この式の右辺と左辺の差は ay_n ですが、

$ay_n = ax_n^2= aA^2 = \frac{1}{n}A^3$

ですから、n を大きくとればいくらでも小さくできます。よって

$S = \frac{1}{3}A^3$

が言えます。しかし、これは現代数学でいえることで、アルキメデスの時代ではこの論法は使えません。というのは A は線分（長さ）で、A³ ＝ A×A×A は「長さ×長さ×長さ」ですから体積です。一方 S は面積ですが、「面積＝体積」という等式は考えられないからです。

今回のお話はアルキメデスの著作の中でもハイライトというべき最も難解な部分です。読者の皆さんの中にはなぜこんなことを思いついたのだろうと不思議に思う人もいるでしょう。天才アルキメデスが、1時間とか2時間なんかではなく、何日も何ヵ月も、ひょっとしたら何年もかかって得た結果です。一読しただけでは理解できなくて当然です。内容さえ分かれば読み飛ばして結構です。