小石の数理
アルキメデスの面積と体積
放物線の求積
2-1. 数と量とは?|古代ギリシアの量の足し算と基本等差列を解説
〔1-1アルキメデスと無限〕で述べたように古代ギリシアの数学では数と量を明確に区別していました。古代の人にとって、“数”とは個数を数えるときにだけ用いる自然数であって、長さや、面積や、体積などは“量”として扱い、“数”と“量”とは全く別物として扱っていました。
現在の私たちにとって、長さ、面積、体積などの量は実数で表され、自然数は実数の特別なものに過ぎません。つまり、自然数も実数なのです。“数”という概念はあまりにも基本的な概念なので、古代の人の“数”がどのようなものであったかを理解するのはとても難しいことだと思います。たとえば、古典期のギリシア人は分数も小数も知らなかったこと、それにもかかわらず高度な論証数学を発展させてきたことなどはにわかには理解できないと思います。したがって、「ギリシア人にとって“数”とは何であったのか」を考えるのは後回しにして、ここではアルキメデスが“量”をどのように扱ってきたのかを述べることにします。
ページ目次
量はどのように扱われていたか
本連載で用いる略記法
ユークリッドの『原論』と同様、アルキメデスも“長さ”とか“面積”とか“体積”という用語は使っていません。線分 AB といったとき、線分 AB 自身を表すときと、線分 AB の長さを表すときとがあります。これは便利なので現在も用います。たとえば、線分 AB と CD に対し、AB = BC と書いたときは、線分 AB の長さと線分 CD の長さが等しいことを表します。
古代では式は用いませんが、本連載では略記法としての式をよく用います。たとえば「三角形ABC」の代わりに △ABC と書きます。たとえば、△ABC = △DEF と書いたとき「2つの三角形 ABC と DEF の面積は等しい」と読みます。本連載では次のような略記法を用います。
〇(r) 半径 r の円の円周
〇2(r) 半径 r の円の面積
□(a,b) 底辺が a 高さが b の長方形
□2(a) 1辺が a の正方形
□3(S, h) 底面がS、高さが h の直方体
□3(a) 1辺が a の立方体
記号 〇2 は円の面積を、□2 は正方形を表す記号で、2乗を意味するものではないことに注意してください。□3 についても同様です。これらは右の言葉の略記法であって、言葉に置き換えることができることにも注意してください。これだけの記号ではとても多くの図形に対処できるものではありません。あとは言葉を使って、たとえば「台形ABCD」などと表すことにします。
同じ種類の量は足すことができる
同じ種類の量は足したり引いたりできます。しかしこれは「実際に足せる方法がある」ことを意味するものではありません。量には大きさがあり、同じ種類の量は、どちらが大きいか、あるいは等しいかが決まっています。これも「どちらが大きいか」を実際に判定する方法があることを意味するものではありません。たとえば、複雑な2つの曲線は、どちらが長いか実際に判定する方法が分かっていないことがあります。重要なことは、種類の異なる量は足したり、大きさを比較することができない、ことです。たとえば、長さと面積は足せませんし、大きさを比べることもできません。
交換法則、分配法則
同じ量は足せますから、自然数倍することができます。量 a と自然数 n に対して na は、a を n 個足した a+a+ … +a を意味します。
自然数 n と m、量 a に関しては次が成立します。
(a) na + ma = (n+m)a
長方形に関しては次が成立します。ここで a, b, c は任意の辺とします。
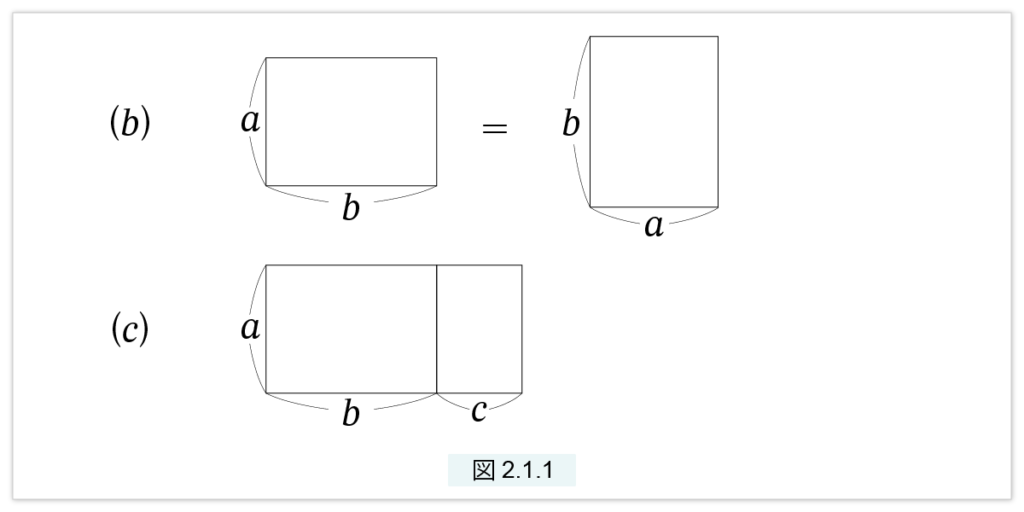
(b) □(a, b) = □(b, a)
(c) □(a, b+c) = □(a, b) + □(a, c)
これを図に表すと以下のようになります(図2.1.1)
□(a, b) を a×b と置き換えると、次となります。
(d) 交換法則 a×b = b×a
(e) 分配法則 a×(b+c) = a×b + a×c
時代が進むと、辺(線分、長さ)は実数とみなされるようになり、(b) は(d) の交換法則、(c) は (e) の分配法則とみなされるようになりますが、アルキメデスの時代ではまだ (b) と (c) は任意の量に対する規則ではなく、辺についてだけ述べたものです。
古代ギリシアにおける量の足し算
円周の足し算
現在の皆さんは、次の式を認めると思います。
2π(r1+r2) = 2πr1 + 2πr2 (1)
この式を、上で述べた古代の方法で書き直すと
〇(r1+r2) = 〇(r1) + 〇(r2) (2)
となります。(2) は次の“言葉”を書き換えたものです。
半径 r1+r2 の円周は、半径 r1 の円周と半径 r2 の円周の和である
しかしこれは、アルキメデスにとって、ただちに成り立つ事柄ではなく、証明を要する事柄なのです。現在の (1) と古代の (2) では意味が違うのです。(2) の左辺の “+” は「長さの足し算」で、長さが線分で与えられた場合は“つなぎ合わせ”で実現されます。一方右辺の “+” は「円周の足し算」ですから、線分と違ってそのままでは足せません。古代の数学を扱う場合は、単純に現代の式に置き換えることができないのです。
面積の足し算
現在の私たちは、長さも面積も体積もみな実数ですから四則演算が自由にできますが、古代では量は数ではないので、演算が非常に制限されていました。面積に関しては、足し算引き算が自由にできるのは長方形に限ります。上で述べた (b) と (c) 以外に次の規則がよく使われます。任意の自然数 n と、辺 a, b に対して次が成立します。
(f) □(na, b) = n□(a, b) = □(a, nb)
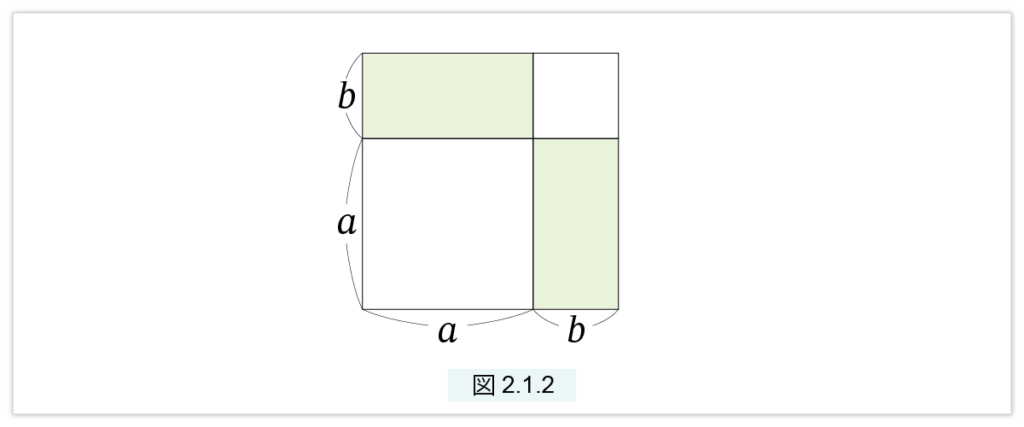
任意の辺 a と b に対して次が成立します。これは 図2.1.2 より明らかです。
□2(a+b) = □2(a) + 2□(a,b) + □2(b)
「量」の列はどのように扱われたか
基本等差列
ギリシアの数学では、数と量をまったく別のものとして扱っています。ユークリッドの『原論』でも、数に対する同じ内容の定理を量に対しても証明しています。アルキメデスも、数の列 1, 2, 3, … にあたる量の列
A, B, C, …
を扱っています。この列は、A から始まり、順次 Aずつ増加する量の列で、現代的な表現で表すと、この列は
1A, 2A, 3A, …
と書けます。このような列を基本等差列と呼ぶことにします(この用語は次の定理を述べるためだけに用います)。
モナド 〜 ギリシアにおける“1” 〜
実は古代ギリシアでは、最初の項を単にA と表し、1A と表すことはありませんでした。ギリシアでは、1(いち)はモナドといって数の仲間にさえ入れていません。現代人でも、日常会話では「私の今持っているお金はきみの持ち金の1倍だ」などとは言いません。このような言い方をするのは数学者だけです。しかし本連載では、現代の読者のため“1” を使うことにしました。
基本等差列の定理
本連載では、上で述べたような式を使いますが、アルキメデスはすべて言葉で表しています。「数学は国語力だ」と言われることもありますが、皆さんは次のアルキメデスの定理の意味が分かりますか。
【定理】基本等差列 1
基本等差列の初項から最後の項の一つ手前までの和の2倍に最後の項を足したものは、最後の項の項数倍に等しい
アルキメデスは項数が5個の基本等差列
A, B, C, D, E
について証明しています。この場合、5は特定の数ではなく“任意の数”を代表しています。上の定理を式で表すと、
2×{A+B+C+D} + E = 5×E (3)
となります。E が最後の項、5 が項数で、5×E は「最後の項の項数倍」です。現代式に表わせば
2 ×{1+2+ …+(n-1)} + n = n2 (4)
となります。
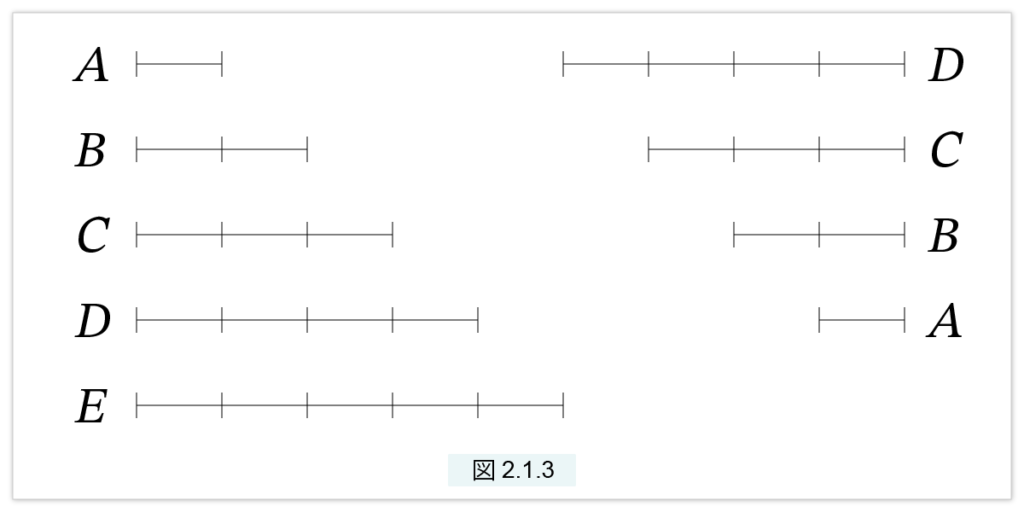
アルキメデスは (3) を、ロープを使って図2.1.3 のように示していますが、現在の私たちには次のような式のほうが分かりやすいかもしれません。
2×{A+B+ … +C+D} + E
= {(A+D)+(B+C)+ … +(D+A)}+ E = n×E
式 (4) は現在の次の公式を言い換えたものにほかなりません。(4) の両辺に n を足して2で割ればこの公式が得られます。
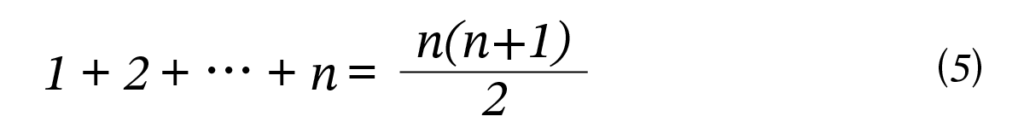
上の〔基本等差列1〕の定理は現在の私たちにとって扱いにくいので次の形で用いることにします。
【定理】基本等差列2
量 A と任意の自然数 n に対して次が成立する。
2×{1A+2A+3A+…+(n-1)A} + nA = n2A
ただし、右辺の n2A は「最後の項 nA が n個」という意味です。実際の応用では上の基本等差列の定理より次の系がよく用いられます。
【系】
2×{1A+2A+3A+…+(n–1)A} < n2A
2×{1A+2A+…+(n–1)A+nA} > n2A
ここで、a を任意の線分とし、A = □2(a) = □(a, a) と置くと、(f) より
1A + 2A + … +(n-1)A
= □(a, 1a)+□(a, 2a)+…+□(a, (n–1)a) )
= □(a,{1+2+…+(n–1)a)
したがって上の定理より
2×□(a,{1+2+…+(n–1)}a) + n□(a,a)= n2□(a,a)
が得られます。また
n2□(a,a) = □(na,na) = □2(na)
ですから、次の定理が得られます。この定理は次節で用います。
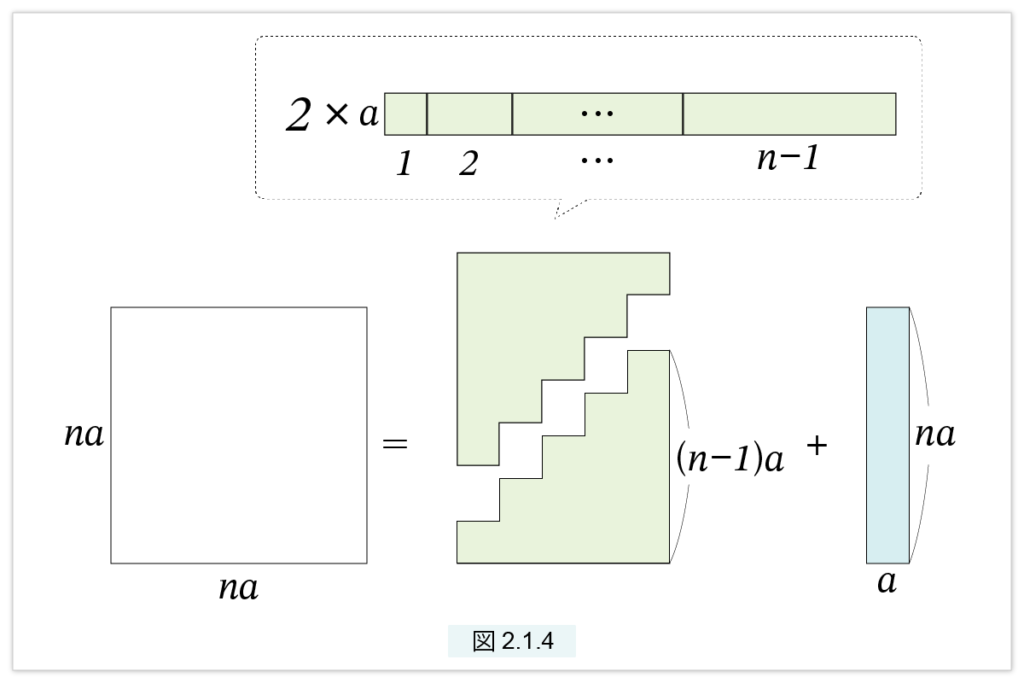
【定理】正方形の3分割
線分 a に対して次が成立する。
□2(na) = 2×□(a, {1+2+…+(n–1)}a) + □(a, na)
図2.1.4 を見てください。一辺が na の正方形は、□(a, na) と2つの階段状の領域に分かれています。階段状の領域の面積は □( a, {1+2+…+(n–1)}a )となります。
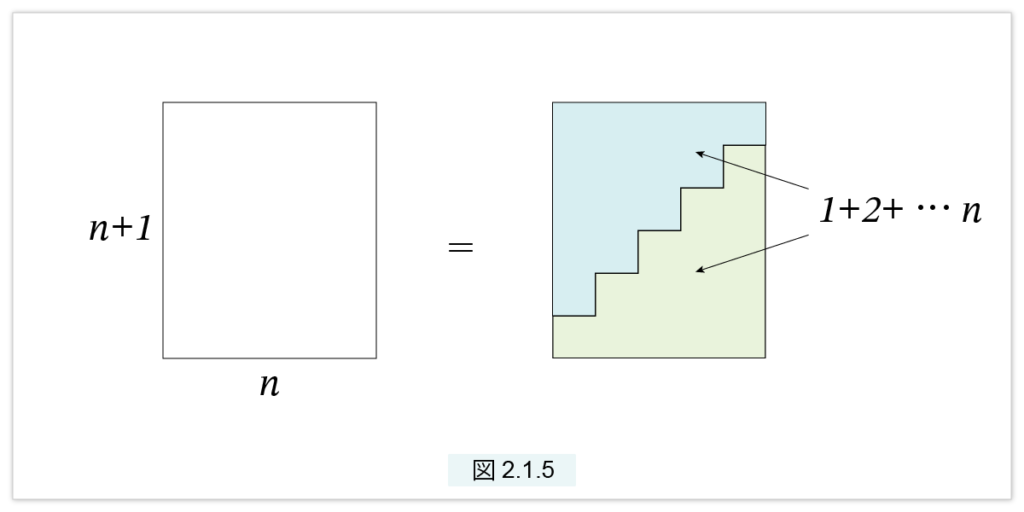
現在の私たちは (5) を公式として覚えます。古代ではこの代わりに 図2.1.5 の図形を覚えました。図は n×(n+1) の準正方形です。青と緑の2つの階段状が 1+2+…+n となります。
PICK UP!!こちらのWeb連載もおすすめです


