第21回 春分の日の計算

現在日本で使われている暦では春分の日は3月21日に固定されてはいません。ときどき20日になったりします。現在私たちが使っている暦はグレゴリオ暦で、そもそも春分の日を太陽の動きに合わせるためにユリウス暦を改めたはずです。それなのになぜ春分の日が固定されていないのでしょうか。

グレゴリオ暦とユリウス暦についてはこちらの記事で詳しく解説しています▼
第13回 グレゴリオ暦：ユリウス暦の改良

第13回 グレゴリオ暦：ユリウス暦の改良

ユリウス通日とグレゴリオ通日

グレゴリオ通日

これまで暦に関するいろいろな計算にグレゴリオ通日を使ってきました。ここでこれらを復習しておきましょう。

古代天文学や歴史学で使われているものは、ユリウス日と呼ばれているもので、これは紀元前4713年を起点とするものです。本連載では、計算を簡略化するため、起点を西暦元年とし、これをユリウス通日と呼ぶことにしました。また、現在使われている暦はグレゴリオ暦なので、グレゴリオ通日という概念も導入しました。これらの三つは本質的には同じで、一方から他方に次のように簡単に変換できます。

ユリウス日 ＝ ユリウス通日 ＋ 1,721,423
ユリウス通日 ＝ グレゴリオ通日 ＋ 2

グレゴリオ通日やユリウス日について詳しく知りたい方は、こちらをぜひご一読ください▼
第17回 ユリウス日：暦の対照

第17回 ユリウス日：暦の対照

グレゴリオ通日と実際の日数の差

グレゴリオ暦は1万年に3日の誤差と述べましたが、これは平均値であって、個々の年における誤差ではありません、たとえば 1903年12月31日のグレゴリオ通日を計算してみましょう。

1903×365 ＋ [1900/4] – [1900/100] ＋ [1900/400]
＝ 693,595 ＋ 475 – 19 ＋ 4 ＝ 695,055                      (1)

一方、天文学的な実際の日数は、1太陽年が 365.2422日ですから、

1903×365.2422 ＝ 695,055.9066                                    (2)

となり、実際の値の方がグレゴリオ通日より約 0.9日大きくなります。実は 1903年が、このあたりでは誤差が最大となるのですが、それでも約1日の誤差となります。以下ではこの

グレゴリオ通日 – 実際の日数

について考えます。式(1) と式(2) を見てください。1903×365 は両式に含まれ、差をとると消えます。そこで次のように式を定義します。

暦年(n) ＝ [n/4] – [n/100]＋[n/400]
太陽年(n) ＝ 0.2422n
差(n) ＝ 暦年(n) – 太陽年(n)                                             (3)

ここで nは、グレゴリオ暦の年数。暦年(n) は n年12月31日のグレゴリオ通日（から 355nを引いたもの）。太陽年(n) は実際 n年間の日数（から 355nを引いたもの）。たとえば 2096年を例に計算してみましょう。

暦年(2096) ＝ [2096/4] – [2096/100]＋[2096/400] ＝ 509
太陽年(2096) ＝ 0.2422×2096 ＝ 507.6512
差(2096) ＝ 509 – 507.6512 ＝ 1.3488

今度はグレゴリオ通日の方が実際に日数より1日以上大きくなります。グレゴリオ暦では、4年、100年、400年、といったわかりやすい規則で日数を調整しています。この方法ではどうしても、プラス・マイナスの両方に約1日の誤差が出てしまいます。

春分の日を決定する方法

春分の日を決定する「表」

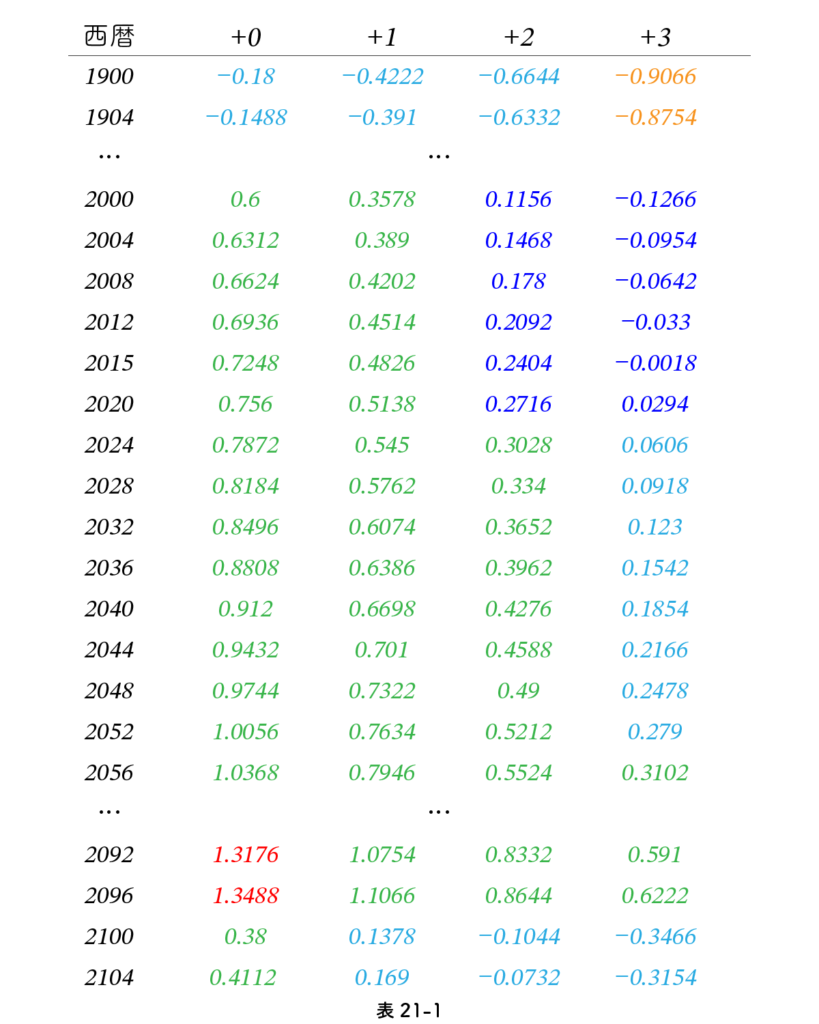
表21-1を見てください。一番上の行は 1900年、1901年、1902年、1903年の“差(n)”です。一般に、左端の列から順に、左端で示された年の ＋0、＋1、＋2、＋3 年の“差”を示します。

春分の日を決定するしきい値

春分の日は、差(n) の値によって西暦 n 年の春分の日が決定されます。

表21-2に置ける 1.28, 0.28, -0.72 のような値をしきい値といいます。式 (3) の 差(n) の定義と表21-2のしきい値があれば、現代の皆さんなら電卓を使って、春分の日がいつの日か簡単に計算できます。

古代ではこのような式はありません。膨大な過去の記録である暦書を用いていました。ヨーロッパ中世の暦算家は数の扱いが苦手で、桁数の大きな数を扱うためのいろいろな工夫がなされていました。また、暦書を丹念に研究することによってそのなかに隠された規則性を発見していきました。近世になると数論が発達し式の変形が可能となります。数学も、他の自然科学と同様に、“実践”という土壌から生まれたのです。以下では式の変形によって、差(n) の計算がどのように簡単に計算できるようになるか、表21-2 にはどのような規則性があるのかを見ていきます。

春分の日決定の数理

整数部分の性質

小数点表示された正の実数 x を考えます。式 [x] は x の整数部分を表します。すると、自然数 n と正の実数 x に対し

[n＋x] ＝ n ＋ [x]

が成立します。したがって、自然数 m, k, n に対して次が成立します。

m が n で割り切れるなら [(m＋k)/n] ＝ m/n ＋ [k/n]

x を 0 ≦ x ＜ 400 となる自然数、n を任意の自然数とするとき

暦年(400n＋x)
＝ [(400n＋x)/4] – [(400n＋x)/100]＋[(400n＋x)/400]
＝ 100n – 4n ＋ n ＋ [x/4] – [x/100]＋[x/400]
＝ 97n ＋ 暦年(x)

よって次が得られます。

差(400n＋x) ＝ 暦年(400n＋x) – 太陽年(400n＋x)
＝ 97n – 0.2422×400n ＋ 暦年(x) – 0.2422x
＝ 0.12n ＋ 差(x)

同様にして、0 ≦ m ＜ 3、 0 ≦ y ＜ 100、 0 ≦ k ＜ 25、 0 ≦ i ＜ 4 なる自然数 m, y, k, i に対して次が成立することがいえます。

差(100m＋y) ＝ -0.22m ＋ 差(y),
差(4k＋i) ＝ 0.0312k ＋ 差(z),
差(i) ＝ -0.2422i

これを整理すると次のようになります。

差(400n＋100m＋4k＋i)
＝ 0.12n – 0.22m ＋ 0.0312k – 0.2422i                 (4)

ためしに上で述べた 差(2096) を計算してみましょう。

差(2096) ＝ 0.12×5 – 0.22×0 ＋ 0.0312×24 – 0.2422×0
＝ 0.6 ＋ 0.7488 ＝ 1.3488

春分の日を計算する「表」の作り方

次に、表21-2の作り方を見てみましょう。これは表21-2の性質を表すものでもあります。式 (4) を頻繁に用います。

まず、表21-2の 2000年の行から2096年の行までの100年間を作成しましょう。差(2000) は (4) より 0.12×5＝0.6 と計算できます。一般にある欄の値が定まっていたら、その値から 0.2422 を引けば右の欄の値が定まります。またその値に 0.0312を足すと下の欄の値が求まります。たとえば 2001年の値は 0.6 – 0.2422 ＝ 0.3578 となり、2004年の値は0.6312 となります。2005年の値は左の値からも、上の値からも計算できます。 　

2100年の行から2196年の行までの100年間の各欄の値は、いま構成した100年間の対応する欄の値から0.22 を引けば得られます。たとえば、2015年の値は、2005年の値 0.389 から0.22 を引いた 0.169 となります。この次の100年、さらに次の100年も、同様に前の100年の各値から0.22 を引いたものになります。これで2000年から400年の値が定まりました。

次の400年、つまり2400年から2799年までの各要素の値は、対応する2000年から2399年の値に 0.12加えることによって得られます。1600年から1999年までの値は、2000年から2399年の値から 0.12を引けば得られます。