第6回 メトン周期：天文学者メトンと閏月

メトン周期とは、暦の19年を235朔望月とする周期で、19年に7回の閏月を挿入する暦法です。これは古代ギリシアの天文学者メトンによって発見されたと言われています。今回はこれについて詳しく調べてみましょう。

古代では小数をどのように扱ったか

1年の日数、1ヶ月の日数

“数“の概念は「物を数えること」から生まれました。人類は太古の昔から日数を数えていました。しかし、1年の日数、1ヵ月の日数は自然数ではありません。次は本連載中に何度か出てきましたが現代のデータです。

1太陽年 ＝ 365.2422日　　　(1)
1朔望月 ＝ 29.53059日　　　(2)

小数は高級な概念で、これを扱うには“数学力”が必要です。このお話では、古代の人がこのような数値をどのように扱ったかを見てみましょう。

古代の暦：月の満ち欠け

古代の暦は月を基準にしていました。『旧約聖書』の詩篇の中にも、「エホバは月を作りて時をつかさどらせたまへり」とあります。また、多くの民族では月が時(とき)を司(つかさど)る神（女神）です。太陽暦のエジプトでも、1ヵ月は30日で、1年は12ヵ月であることから、もともとは月を基準としていたことがわかります。月の満ち欠けを見れば、日数の経過が分かりますし、12ヵ月は1年を区切るのにちょうどいい区間です。

平朔(へいさく)法

新月から次の新月までの日数を数える

まず、1ヵ月の長さ (2) を見てみましょう。発明・発見は同時に独立になされた可能性があります。紀元前では中国とオリエントはおそらくほとんど交流がなかったと思われます。ここで古代中国を見てみましょう。新月から次の新月まで（あるいは満月から次の満月まで）の日数を数えると、29日か30日になります。29日の月を「小の月」、30日の月を「大の月」と呼ぶことにします。長いあいだ数えていると、やがて小の月と大の月を交互に繰り返すとだいたいうまくいくことに気がついたと思います。

大の月と小の月をどのように並べるか

ここで現代の数学の概念である小数を使って考えます。小の月と大の月を繰り返すということは、1ヵ月を 29.5日見なしていることになります。まだ 0.03059 残りますが、33倍か34倍すると1に近くなりそうです。34倍することにします（33の方が数値としては1に近くなるのですが、33は奇数なので後の処置がうまくいきません）。

0.03059×34 ＝ 1.04006

つまり、34ヵ月ごとに1日を加えると、残りの小数部が消化できます。具体的には大の月と小の月を次のように並べます。

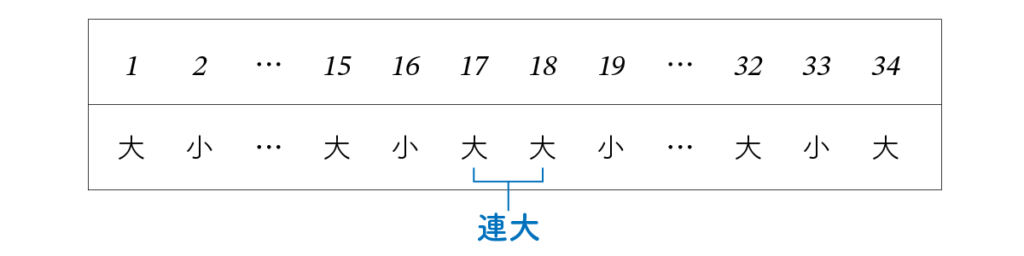
大大と大の月を並べることを連大といいます。第十七月と第十八月が連大となっています。この方法は「平朔(へいさく)法」といい唐時代まで用いられていました。これを直輸入した日本も平朔法が使われていました。

「1日の挿入」による調整

実はこの平朔法には欠点があります。実は (2) の1朔望月は平均値なのです。太陽の周りを回る地球の軌道は円ではなく、楕円です。したがって、「1日＝24時間」というのも平均値で、正確には、1日の長さは夏と冬では違うのです。同様の理由で、1朔望月も季節によって違います。したがって、月の形を正確に暦に合わせようとすると、季節まで考慮しなければなりません。さらに、この方法には大きな欠点があります。この方法には“年”が考慮されていないのです。暦は“年”を単位に設定されます。そこで、1朔望月を12倍します。

29.53059日 × 12 ＝ 354.36708日　　　(3)

右辺の 354.36708日 を1太陰年と呼ぶことにします。ここでも現代数学を使って考えましょう。小数部 0.36708 を分数で近似すると、

3/8 = 0.375, 4/11 = 0.3636…,
7/19 = 0.3682…, 11/30 = 0.3666…　　　(4)

となります。7/19 を例に説明しましょう。小数部は19倍すると整数 7 となります。すなわち、19太陰年のうち7年の各年に1日を挿入し、残りの12年はそのままとすれば小数部が消化できます。実際に計算してみましょう。

19太陰年 ＝ 354.36708日 × 19 ＝ 6732.97452日
≒ ( 354 + 7/19 日) × 19 ＝ 6733日

となり、19太陰年で 0.02548日の誤差となります。

「1日の挿入」は、小の月の一つを大の月に変えれば実現できます。現在、イスラームの国の多くが使っているヒジュラ暦は太陰暦ですが、分数近似 11/30 を採っています。これについては〔 第8回 暦の伝播 〕で解説します。

太陽暦と太陰暦

太陽暦・太陰暦、両方を満たすには？

次に太陽暦と太陰暦をうまく組み合わせる方法について考えましょう。太陽暦の1年は1太陽年、太陰暦の1ヵ月は1朔望月です。そこで次のような自然数 n と m を考えます。

365.2422×n ≒ 29.53059×m　　　(5)

このような n と m が見つかれば、「n年を mヵ月」と設定すれば、太陽暦と太陰暦を両方満足できます。(5) を分数に直してみましょう。

m/n ≒ 365.2422/29.53059 = 12.36826626　　　(6)

これはまったくの偶然の一致ですが、(3) の小数部 0.367 と (6) の小数部 0.368 がほとんど一致するのです。このような不思議な偶然の一致がよくあるのです。これは誤解を招くことが多いので注意しましょう。今度の場合も (4) と同じ分数近似が使えます。7/19 を使ってみましょう。

365.2422/29.53059 ≒ 12 + 7/19

ですから、

365.2422×19 ≒ 29.53059×12×19＋29.53059×7

となります。したがって、

19太陽年 ≒ 19×(12朔望月) ＋ 7×朔望月 ＝ 235朔望月

となります。

十九年七閏)の法：メトン 法

上で述べた 7/19 を使って太陰暦を補修する場合、19太陰年のうち7太陰年に1日の閏日を挿入しました。つまり、19年で7回、29日の小の月に1日の閏日を加え30日の大の月にしました。今度の場合は、19太陰年で7回朔望月を挿入するのです。つまり、12ヵ月の1年に閏月を加えた13ヵ月の年を作ります。閏月を加えられて13ヵ月となった年を閏年と呼びます。これを「十九年七閏(じゅん)の法」といいます。どのくらいの誤差かを見てみましょう。

235朔望月 ＝ 235×29.53059 日 ＝ 6939.68865 日
19太陽年 ＝ 19×365.2422 日 ＝ 6939.6018 日

19太陽年との差はわずか 0.08685日、つまり2時間5分にすぎません。

分数近似 3/8 を用いると、8太陰年に３回の閏月を加えるという、「八年三閏(じゅん)の法」となります。〔第3回 メソポタミアの暦〕で述べたように、紀元前22世紀のウル第3王朝の粘土板文書に「八年三閏(じゅん)の法」の暦の記録があります。また、紀元前8世紀頃のバビロニアの粘土板には「十九年七閏(じゅん)の法」の適用例があります。この「十九年七閏(じゅん)の法」という名称は古代中国のもので、古代中国でもこの方法を用いていました。「十九年七閏(じゅん)の法」は現在ではメトン法と呼ばれています。この方法については、もう少し述べなければいけないことがあるのですが、それはこの記事の最後のところで述べます。

３つの方法の違い

ここまでで紹介した暦法をまとめると以下のようになります。

「平朔法」：34ヵ月ごとに「1日」を挿入。“年”を考慮していない。
「1日挿入法」： 19太陰年のうち7年に「1日」を挿入。太陰暦。
「メトン法」：十九年七閏の法。太陰太陽暦。19太陰年のうち7年に「1朔望月」を挿入。

古代エジプトの暦

古代エジプトでも月の観測値を利用していた

次に古代エジプトの暦を見てみましょう。エジプトの民衆暦は太陽暦でしたが、太陰暦も用いていたことが知られています。中王朝時代のパピルス•テキストによると、その暦は1年が354日で、2年か3年に1度閏月を挿入しています。さらに正確にいうと、その暦は民衆暦の25年に309個の朔望月を設定していました。これは民衆暦（太陽暦）を使って、夕方に月を観測して新月が現れたらチェックを入れるという方法を25年間続ければ発見できます。おそらく25年間の観察1回というのではなく、何度も繰り返して得られた結果だと思います。エジプトの民衆暦の1年は365日です。1年に1朔望月が何個入るかを計算し、小数部を分数で近似します。

365/29.53059 = 12.3600646 ≒ 12 + 9/25 = 12.36

この式より、1年は12ヵ月と 9/25 ということが分かります。したがって、25年に9個の朔望月を挿入すればいいことが分かります。実際にエジプトの太陰暦はこのようになっていました。どのくらい正確か検算してみましょう。

25年の朔望月 ＝ 12×25 ＋ 9 ＝ 309 (朔望月)
25年の日数 ＝ 25×365 ＝ 9125 (日)

ですから、1朔望月の平均の日数は

9125÷309 ＝ 29.5307

ですから、現在の一朔望月の値 29.53059 にとても近い正確な値となっています。

メトン周期はメトンの発見か

天文学者メトンが測定したもの

メトン周期とは、暦の19年を235朔望月とする周期で、ギリシアの天文学者メトンが発見したというのが現在の定説となっています。しかしこれは上で述べた「十九年七閏(じゅん)の法」にほかならず、バビロニアではメトンが発見するはるか以前から用いられていました。ではメトンが独立に発見したのでしょうか。以下ではこれを検証しましょう。伝承では、具体的な次のような記述もあります。

「メトンは紀元前433年から432年にかけて、夏至と冬至を観測することによってメトン周期を発見した」

メトンが測定したとしているのは、1太陽年と1朔望月だと思います。〔 第1回 暦の始まり 〕で述べたように、夏至とか冬至の観察で太陽年を正確に測定するのは難しいと思うのですが、ここではそれが可能であったとしましょう。すると1年は 365日か、あるいは366日となります。古典期のギリシアには分数も小数もありません。「1年＝365日と見なした」とします。すると、12朔望月≒ 29.5×12日 ＝ 354日ですから、1年で11日余分です。2年で22日、3年で33日、… と順に数えていったと思います。すると8年で 88日、88＝ 29×2＋30 となります。つまり、8年で29日の月を2回、30日の月を1回とれば 88日となります。19年でなく8年で十分なのです。これは「八年三閏(じゅん)の法」です。「1年を366日」とした場合でも、1年で12日余分ですから、5年で60日、30日の月2回分です。もちろんこの考察だけで「メトンの発見」を否定することはできません。メトンがどのような計測と考察を行ったか分かっていないからです。

メトン法の弱点

しかしメトン法には重大な欠陥があります。メトン法は19太陽年が235朔望月とほぼ等しいという事実に拠(よ)るのですが、235朔望月は 6939.68865日 と整数ではありません。実際に割り当てる月は、30日の大の月か、29日の小の月です。ですから6939日か6940日のどちらかとなりますが、どちらか一方に固定するわけには行けません。つまり、19年1回の調整ではなく、19年ごとに大の月と小の月の並び方を変え、数回にわたって調整する必要があるのです。

さらに重大な欠陥は、1朔望月＝29.53059日 という数値が平均値だという事実を考慮していない点にあります。上の平朔(へいさく)法で述べたように1朔望月の長さは季節によって変化します。したがって、大の月・小の月の割り当ても季節を考慮しなければならないのです。バビロニアの天文学者はこの事実を認識していました。つまり、太陰太陽暦の作成において、メトン法は一つの目安に過ぎず、あまり大きな助けにはなっていなかったのです。

〔第15回 日本の暦〕で日本の暦について述べます。そこで日本（中国）でどのようにして太陰太陽暦が作られたのかを解説します。「十九年七閏の法」は自然に導かれる方法ではありますが、暦の作成において大きな役割を果たしてはいません。