第5回 黄道とは?天球上の太陽の通り道を図でわかりやすく解説
ページ目次
太陽の一年の動き、年周運動
天球モデル
皆さんは夜空を見上げて星の動きを観察したことはありますか?夜空に輝くたくさんの星々は、プラネタリウムの天井に映しだされた星々のように見えます。古代の人々は、星々は天球に貼りつけられていると考えていました。では太陽についてはどのように考えていたのでしょうか。毎日太陽は天球と共に地球を一周します。これを日周運動といいます。さらに太陽は、1年をかけて天球の星々の間を旅すると考えてられていました。これを年周運動といいます。ここでは年周運動と太陽の通り道「黄道」について見てみましょう。
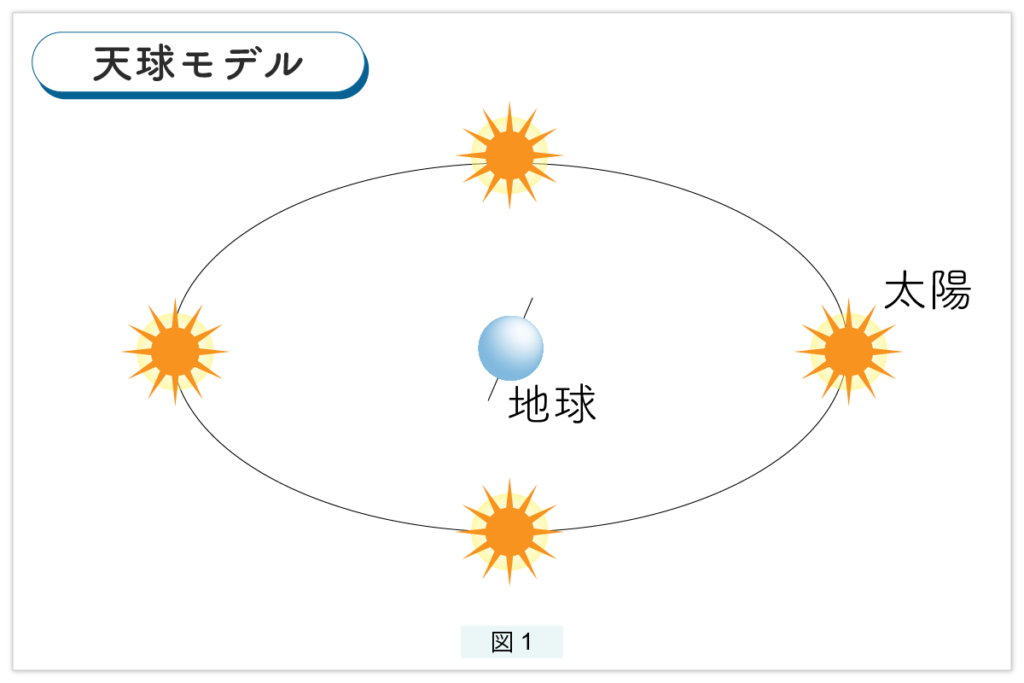
図1では、地球が不動で太陽が地球のまわりを回っていると考えます。これを天球モデルと呼びます。図1 の地球を天球の中心に置けば、これまで扱ってきた天球モデルとなります。
太陽系モデル
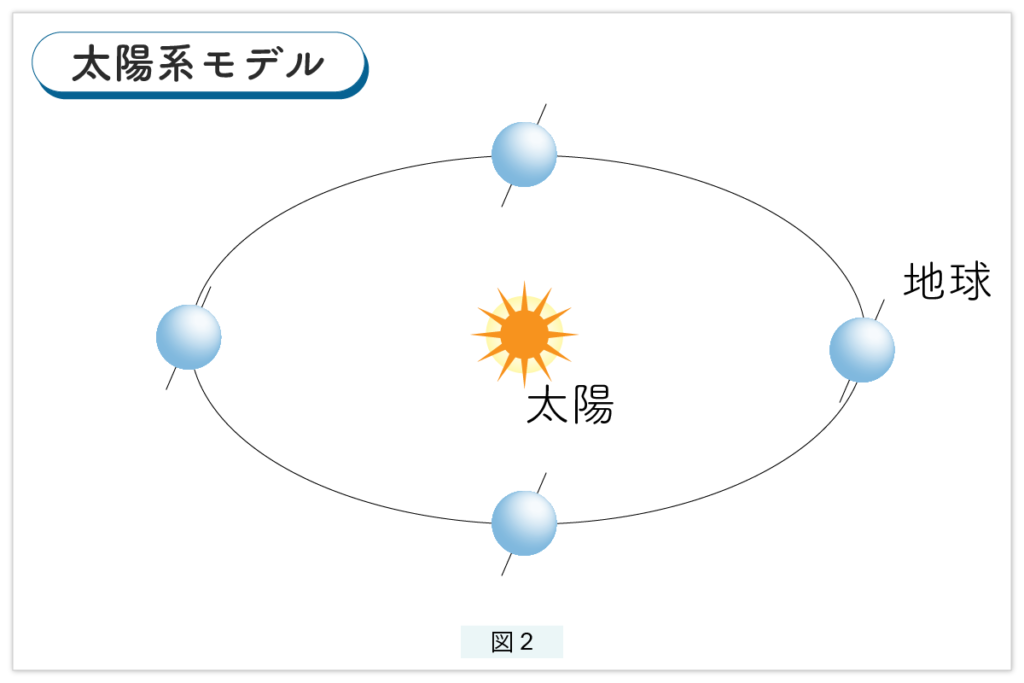
一方図2では、太陽が不動で地球が太陽のまわりを回っています。これを太陽系モデルと呼ぶことにします。太陽系モデルについても、太陽と地球のまわりには広大な宇宙が広がっています。太陽と地球の距離に比べ、星々はとても遠いところにあるので、太陽系モデルにおいても宇宙は天球と考えて支障はありません。
真夜中に南中する星の観察
毎日同じ時間に観察すると?
〔 第3回 地球と日周運動 〕では星々の一日の動き、日周運動について見てきましたが、今回は太陽の1年の動き、年周運動について詳しく見てみましょう。日周運動を年周運動から切り離し、年周運動だけについて考えます。それには天球を固定する必要があります。どのように考えたらよいかみてみましょう。
夜、南の空を眺めていると思ってください。現在の皆さんは正確な時計を持っています。太陽や星が東の山から昇り、やがて子午線を通過します。真南である必要はありませんが、南の地平線にある適当な山か建物を見つけ、その真上に来た適当な星に注目します。その星を毎日、夜の12時に観察するとします(図3)。
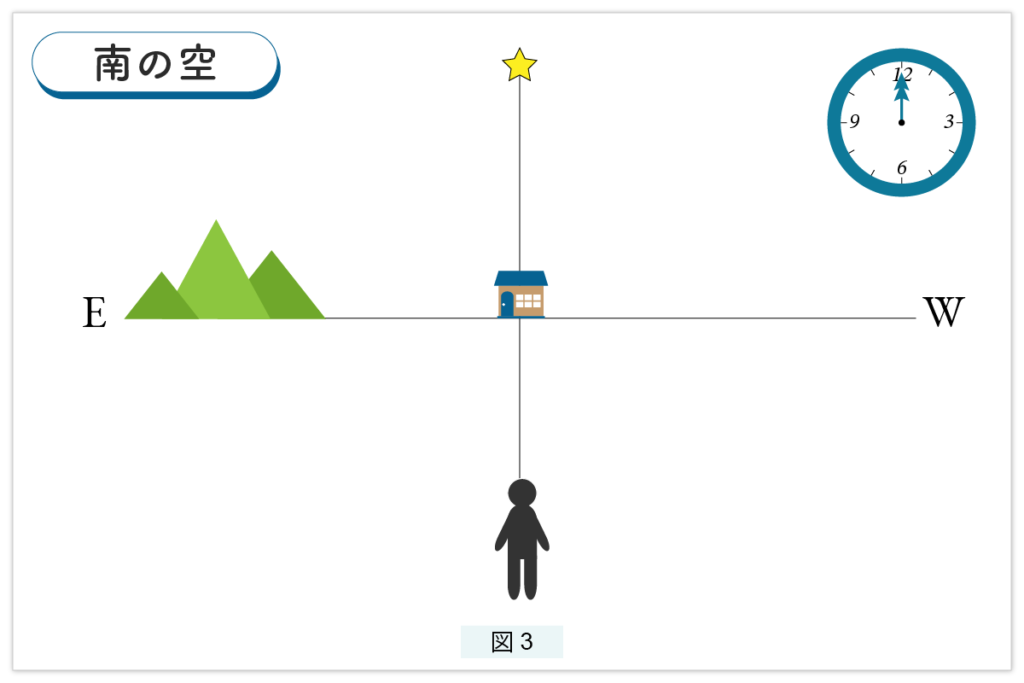
その星は次の日の12時には同じ位置にはなく、少し西に移動しています。1日ですと動きは少ないですが、1ヵ月もするとだいぶ西に動いています( 図4 )。
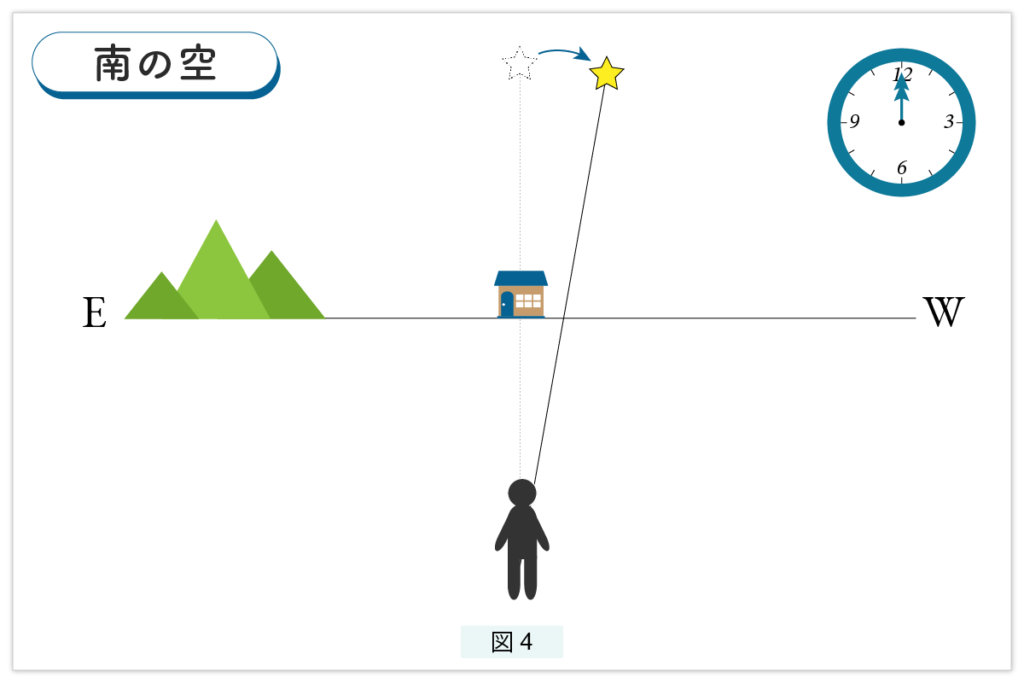
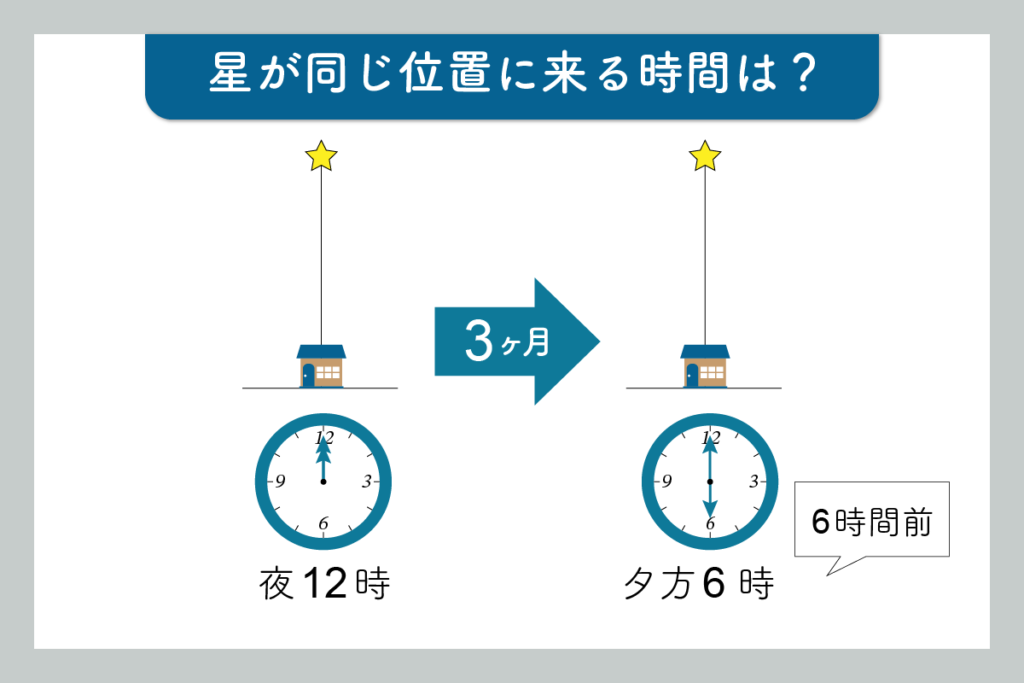
星が同じ位置に来る時間は?
星は1日経つとどれぐらい移動するのでしょうか。大まかな動きを理解するために、単純化して考えてみましょう。ここでは1年を360日と見なします。1年経つと星はまた同じ位置に戻ってきます。円は一回り360度、1年を360日と考えると、1日1度西へ移動します。3ヵ月(90日)なら90度です。
これまでは時間を夜の12時に固定しましたが、こんどは時間ではなく星を固定しましょう。つまり天球を固定します。ある日、夜の12時に南の空のある星を見ています。次の日の12時にはその星は前日見ていた位置を通り過ぎてしまっていますから、時間を巻き戻す必要があります。
1日 = 24時間 = 24×60分
ですから、1度移動するのにかかる時間は (24×60分)/360 = 4分 です。したがって、その星が前日と同じ位置にいたのは12時の4分前のことです。日を追うごとに時間は早くなります。3ヵ月経つと、4分×90 = 6時間ですから、その星が南の空の同じ位置に来るのは夜の12時の6時間前、つまり夕方の6時で、太陽が西の空に沈むころです。
太陽の通り道、黄道とは
天球上の太陽の動き:西から東へ
このような見方で天球を固定すると、太陽は1日に1度西から東に移動することになります。
春分の日と秋分の日は、太陽は朝6時に真東から昇り、昼の12時に南中し、夕方6時に西の地平線に沈みます。春分の日の夕方 6時に南の空の星を眺めていると思ってください。実際には昼間に星は見えませんが、見えているものと想像します。
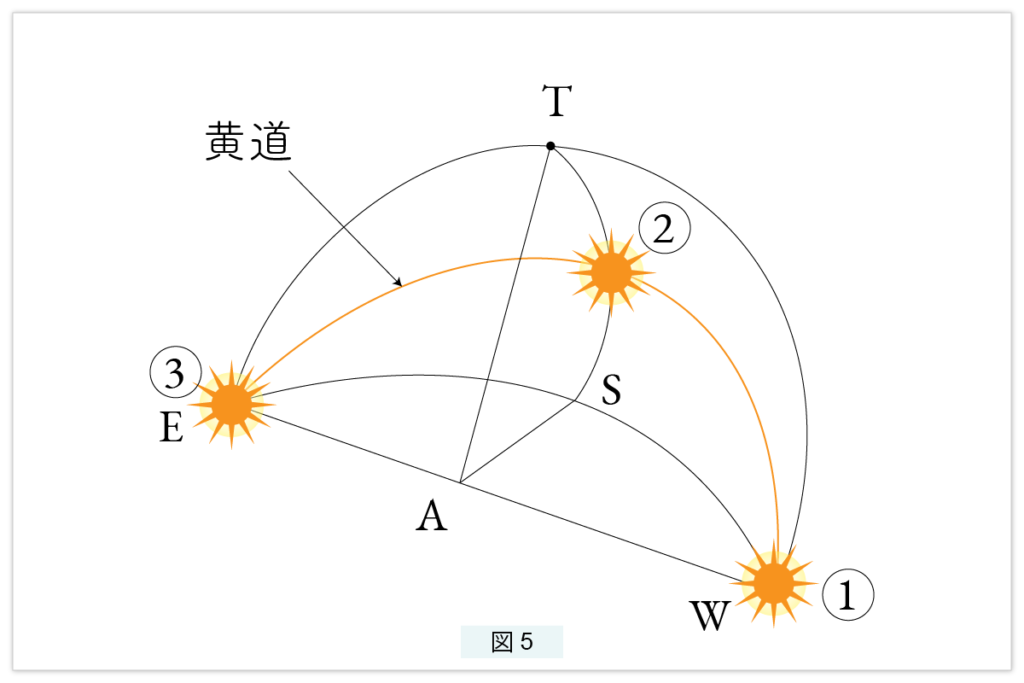
太陽は図5の ① にあります。毎日(実際には見えない)その星が南の空の同じ位置にあるのを見ているとします。次の日、24時間後では行き過ぎてしまいますから、23時間56分後に観測します。すると星は同じ位置にとどまっています。すると、時刻は毎日4分ずつ早くなります。つまり西の地平線 ① にあった太陽は、1日に1度ずつ東へ移動します。このように天球を移動する太陽の道が黄道です。3ヵ月経ち夏至になると、太陽は12時に南中します(図5の ②)。さらに3が月経って、秋分の日になると、朝6時に太陽は東の地平線に達します(図5の ③)。これで天球の半分の黄道が描けました。この後、太陽は地平線の下にもぐります。
天球モデルの考え方
もう一度天球モデルで見てみましょう(図1′)。
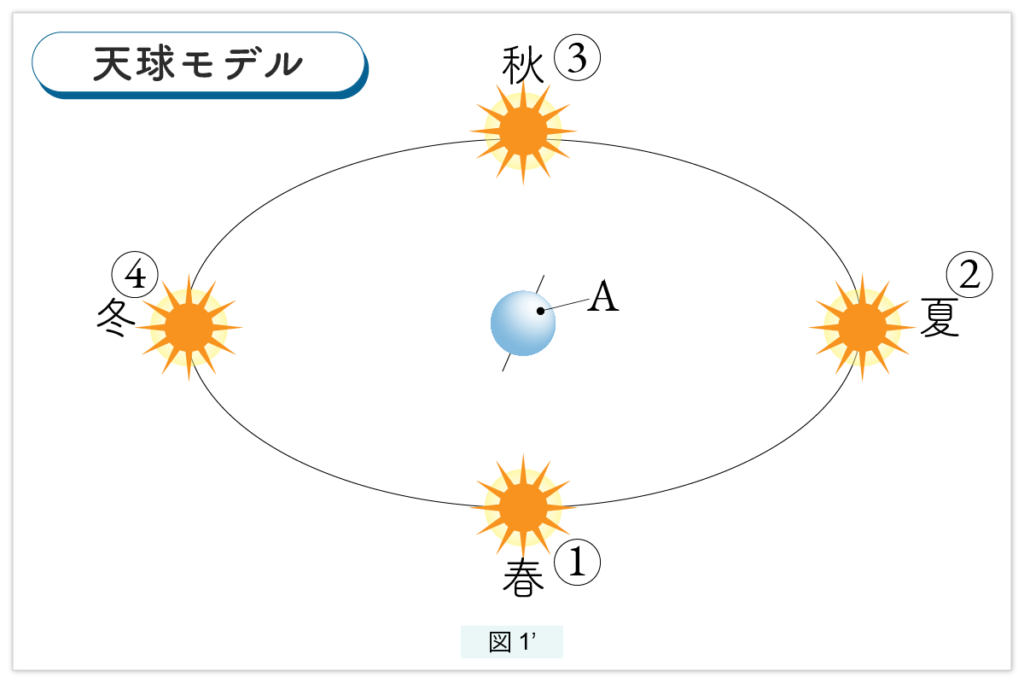
地軸が太陽の方を向いている ② が夏至の日です。真ん中の地球の上の方にある点 A が観測者です。地球は固定され、太陽が反時計回りに回転していると考えます。春分の日に ① を出発します。太陽は西の地平線にあり今まさに日が沈むところ、夕方の6時です。夏至には太陽は南の ② にきます。太陽は南中していますから12時です。秋分の日には ③ にきます。
太陽系モデルの考え方
次に太陽系モデルを見てみましょう(図2′)。
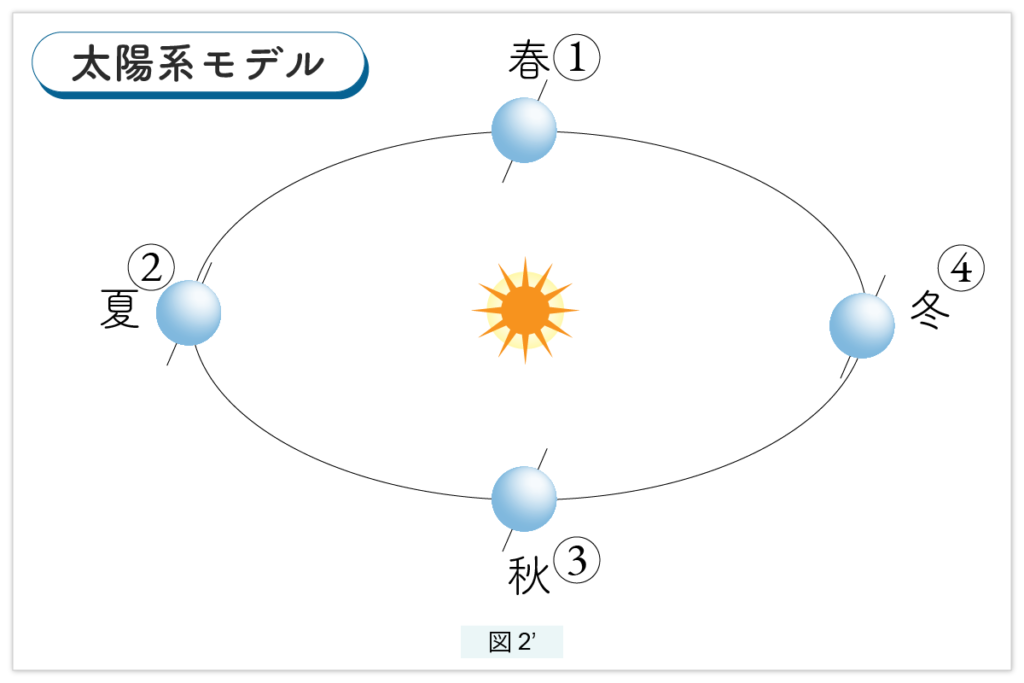
春分の日には ① にいて、下にある太陽を見ています。地球は反時計回りに自転していますから今夕方6時 で、太陽は西にあります。夏至の日には ② にいて南中している太陽を見ています。秋分の日には ③ にいて日の出の太陽を見ています。
図1は天球が動く天動説によるモデル、図2は地球が動く地動説によるモデルですが、どちらのモデルで考えてもまったく同じ振る舞いをします。
太陽と地球の関係を表す模式図
図1と 図2 の地球を模式的に表すと次の図6のようになります。( 第4回 天球モデル –図4と同じ図)この図は太陽と地球の関係を述べる時に使われます。
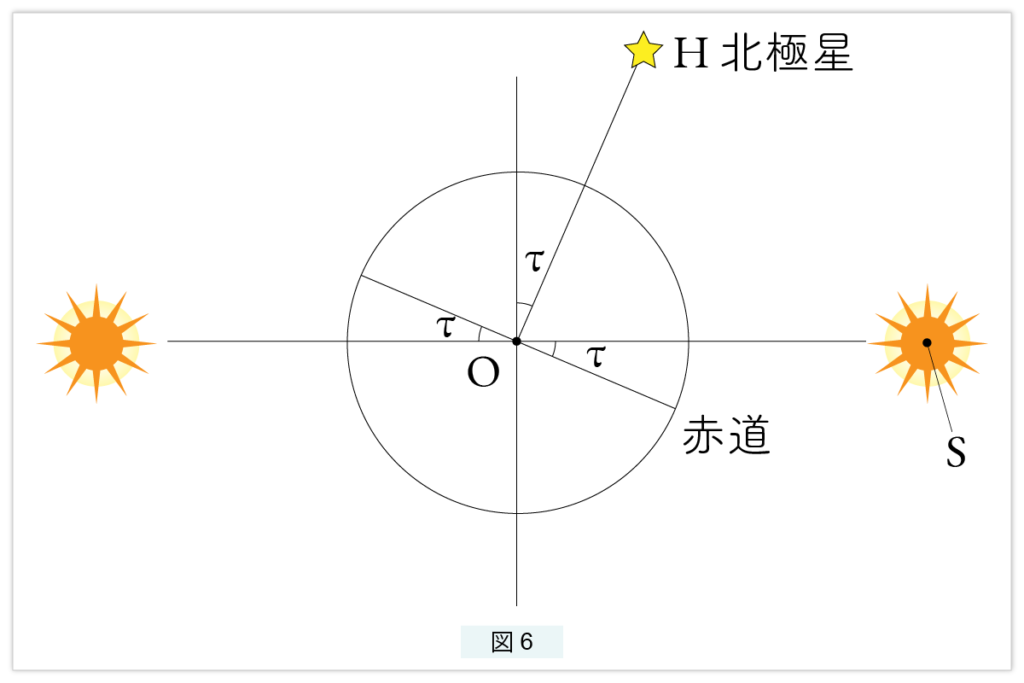
H は北極星で、OH は地軸です。地軸に垂直で O を中心とする大円が赤道です。太陽系モデルでは地球は太陽 S を中心とした半径 OS の円周(公転軌道)を回り、天球モデルでは太陽は地球 O を中心とした半径 OS の円周(黄道)を回ります。太陽系モデルの軌道面が天球モデルの黄道に対応します。この黄道(軌道面)と赤道のなす角を傾斜角といいます。この傾斜角を以下では τ (タウ)で引用します。
τ = 23.4度
傾斜角とは、Oを通り軌道面に垂直に立てた線からの地軸の傾きでもあります。
3次元の立体はいろいろな表し方があり、慣れないうちは混乱するかもしれません。例えば図1 で示される天球モデルでは、現在 ① の春側から見ていますが、② の秋側から見ると、地軸は逆に傾き、夏と秋も逆になります。また、前回のお話〔天球モデル〕で述べたように、地軸の傾きもいろいろ表し方があります。図1 の地球は図6で示されるように、黄道は水平に描かれています。
一方図5 は観測者の視点で見た天球です。この図では観測者が地球の真上に立っています。(宇宙の不思議:天球モデル-図3参照)図5は地平線が水平に描かれており、観測者が太陽や星々を眺めている図です。直観的に理解しやすいのですが、赤道、黄道、地平線などを考えると図1との関係が少し複雑になります。このお話はまた改めて説明したいと思います。



