第12回 恒星月・朔望月とは？ 月の動きを図でわかりやすく解説

朔望月と恒星月

日ごとに姿を変える月は、日時の経過を知らせてくれる暦として古代から親しまれてきました。地球は太陽のまわりを公転し、月は地球のまわりを公転しています。今回のお話では月と地球の動きについて、もう少し詳しく見てみましょう。

1恒星月とは何か

1ヵ月の定義としては、〔第9回 月の不思議〕で、1朔望月を「満月から次の満月までの時間」と定義しました。これまで使ってきた概念を使うと、1朔望月は「1太陽月」と呼ぶことができます。正確な値として現在では次が分かっています。

1朔望月 = 29.53059日

“恒星年”、“恒星日”と同様に1恒星月も次のように定義されます。

1朔望月と1恒星月の差

1恒星月を計算してみましょう。図1 を見てください。A, B, C は地球で、D, E, F は月です。D と F は満月で、したがって、A から C までの期間が1朔望月です。AD の方向に仮想的な星があると考えます。月は地球のまわりを反時計回りに回り、E で天球の同じ位置まで戻ってきています。つまり月はここまでで、360度回転しています。AからBまでの期間が 1恒星月です。

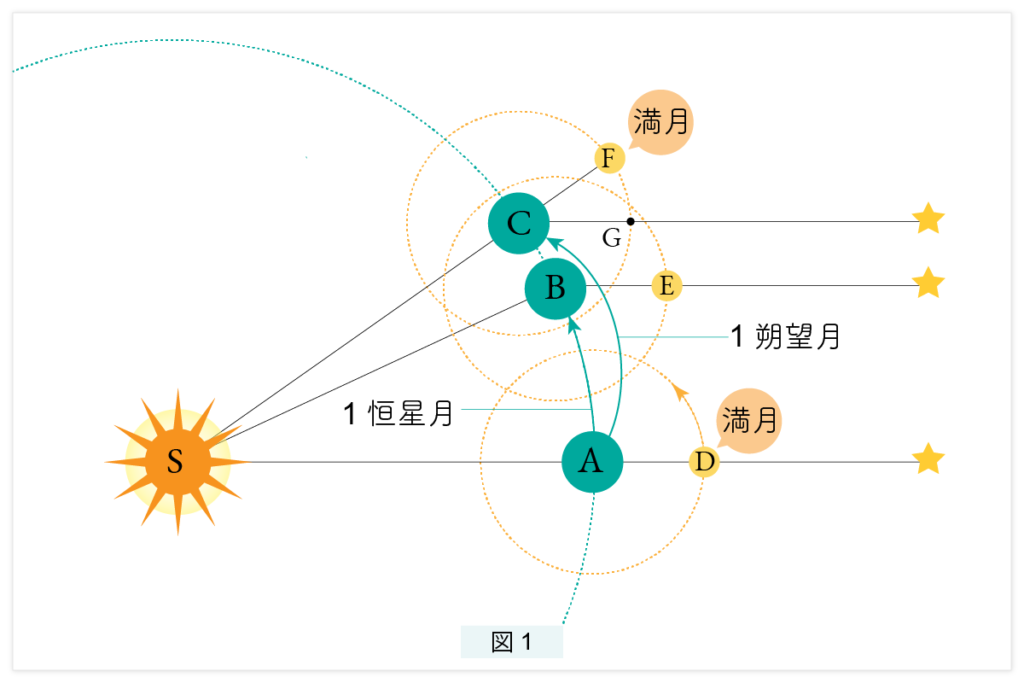
地球 C で月を観測していると思ってください。点 G を、CG がSA と平行になるようにとります。実際は1ヵ月前にAにいて月D を見ていたのですが、C で観測している人は、1ヵ月前に G から出発して地球を1周して G に戻り、さらに F まで進んだように見えます。このうち G からF への回転は、月の公転によるものではありません。仮に月が公転していないとしましょう。A にいた地球が公転してC に移ると、それに連れられてD にいた月はF に移ります。つまり G から F への移動は、月の公転によるものではなく、地球の公転によるものです。

1恒星月の計算

それでは月が1日当たり何度回転するかを計算してみましょう。CG と SA は平行ですから、

∠FCG = ∠CSA

です。∠FCG は地球が A からC に公転したためのもので、月の公転によるものではありません。月の公転が寄与した角度は G-G-F のうち G-G の360度です。∠FCG ＝ ∠CSA で、地球が360度太陽のまわりを回転するのは１恒星年ですから、1日当たり

360 ÷ 365.256363 = 0.9856091131 (約1度)　　　　(1)

となります。一方、月は G-G の360度を1朔望月かかって回転しますから、1日当たり

360 ÷ 29.53059 = 12.19074864 (約12度)　　　(2)

となります。(1) と (2) の合計は約13度となります。したがって、図1 で、月はG を出発し、1日約13度回転し、B でちょうど 360度回転します。以上より1恒星月は次で計算できます。

1恒星月 = 360 ÷ ( 12.19074864 + 0.9856091131 )
= 27.32166254　　　(3)

月の1ヵ月の動き

今述べたことを簡略化してまとめると次のようになります。（図2）

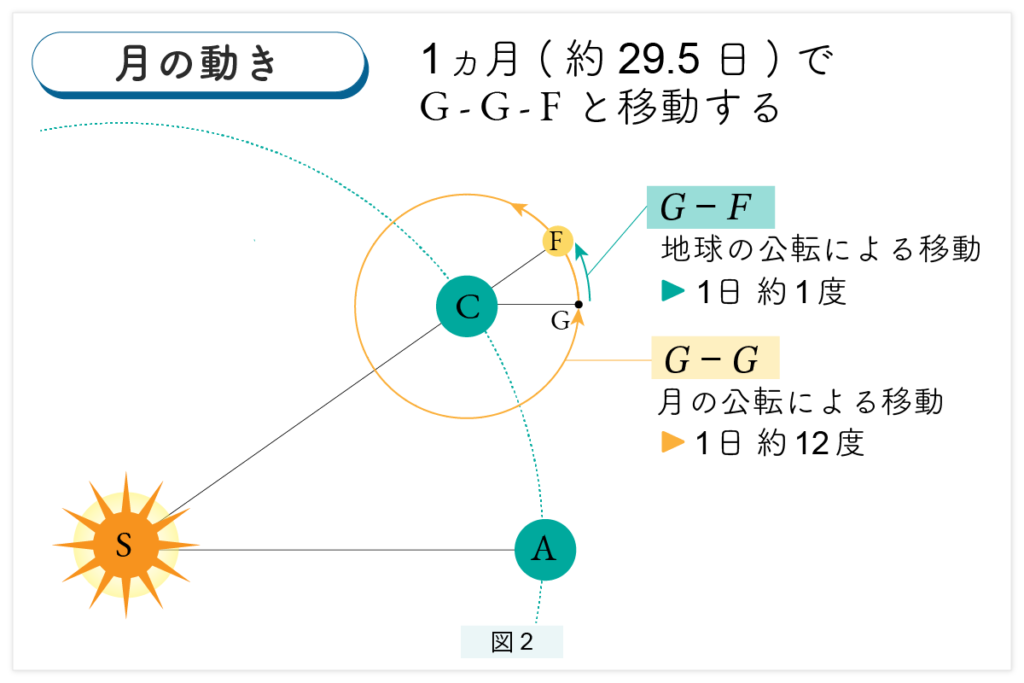
地球にいる人は地球が公転している意識はありませんから、ずっと C で月を観測していると思っています。1ヵ月（29.5日）で月は G-G-F と移動します。このうち G-G は月の公転による移動、G-F は地球の公転による移動です。月の公転による移動は1ヵ月で360°ですから1日当たり 12°、地球の公転による移動は1日1°、したがって計 13°です。つまり、1日13°で G-G-F と移動します。G-G は 360°ですから、G-G を移動するのに必要な日数の概算は 360/13 で計算できます。

月の動きと星の動き

星の1日の動き

正確な値は覚えるのが大変なので、まずはおおざっぱに捉えてみましょう。バビロニア人は、1年が365日と1/4日であることを知っていましたが、天文学だけでなく経済でも、年利を日割りで計算する際、1年を360日として計算していました。バビロニアは60進数だったので、これはとても計算しやすかったのです。次のように簡略化することにします。

1年 = 360日 = 12ヵ月
1ヵ月 = 30日

ある満月の夜、0:00 に南中している満月を見ていると思ってください。毎晩 0:00 に南の空を観測します。〔第5回 太陽の通り道〕で述べたように、星々（天球）は毎日1度西に移動します。

月の1日の動き

これに対し月はどうでしょうか。月の出は毎日遅れます。ということは、月は星々と違って東に移動します。30日経つとまた満月にもどりますから、1日に

360度 ÷ 30 = 12度

移動します。つまり、24時間後には月は東に12度移動し、星々は西に1度移動します。上で計算した (2) の12度と、(1) の1度です。27日経ったらどうなるでしょう。月は東に 12度×27 ＝ 324度、星々は西に27度移動します。合計 351度だからまだ出会いません。28日後は、月は東に 12度×28 ＝ 336度、星々は西に28度移動します。合計は 360度を越えています。したがって、月は27日と28日の間のどこかで前の位置に戻ったことが分かります。正確には、上で計算した (3) の 1恒星月＝27.3日に天球の前の位置に戻ります。

中国の二十八宿

天球における太陽の通り道を黄道といいます。同様に、月の通り道を白道といいます。おおざっぱに見ると、白道は黄道とほとんど同じとみてよいでしょう。古代インドや中国では、白道（黄道）の近くにある星座を28個選んでいます。中国ではこれを二十八宿と呼んでいます。インドでは紀元前800年のテキストに28個の星座が現われますが、その後27個に減らされ、現在まで続いています。

1年の経過を知るには

〔第2回 1週間はなぜ7日になったのか？〕で述べたように、日本の星占いである宿曜道（仏教の宿曜経）はインドから伝わったと考えられています。月の相（上弦、望、下弦、朔）が分かれば、月の経過を知ることができるのに、なぜ二十八宿を考えたのでしょうか。満月の日は、地球の裏側に太陽があります。したがって、現在満月がどの星座にあるかが分かれば、太陽が天球のどのあたりにあるかが分かり、現時点が1年のどのあたりかが分かります。月の相だけでは季節の移り変わりまでは分かりません。月と星座を組み合わせることによって1年の経過を知ったのです。

太陽と地球の関係、月と地球の関係

月の動きを天球モデルで考える

地球のまわりを太陽が回る天球モデルと、太陽のまわりを地球が回る太陽系モデルでは、太陽と地球の相対関係はどちらのモデルで議論しても同じです。地球のまわりを回っている月を太陽に置き換えると天球モデルとなります。したがって、太陽で起こっていることが12倍の速さで月に起きます。

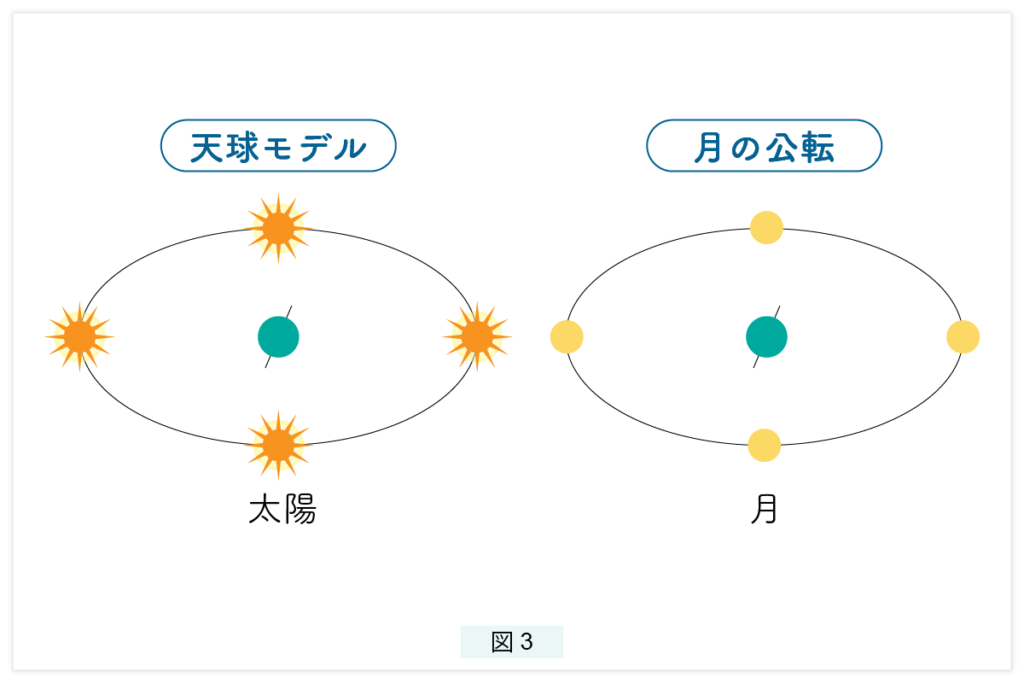
例えば太陽の場合、日の出の位置は最も北寄りの夏至の日の位置から、最も南寄りの冬至の日の位置まで、1年かけて往復します。これに対して月は、最も北寄りの位置から、最も南寄りの位置まで、1ヵ月かけて往復します。

「月の出」の遅れ

太陽は黄道上を1日に約1度、時間にして約4分移動します。月は白道上を1日に約12度、時間にして約50分移動します。これらは概算で、1年を通しての平均値だと思ってください。「太陽が1日約1度（4分）東に移動する」ことを「日の出が毎日約4分遅れる」ことだと勘違いしている人がいるようですから注意してください。天球を固定した議論では、時間を毎日4分遡るということであって、日の出は遅れていません。

日の出と日の入りの時間は、その土地の緯度や経度その土地の標準時、地形などいろいろな要素に依存しています。しかし月の場合、上で計算したように1日に12度、時間にして 12×4＝48分遅れます。つまり南中してから次に南中するまでの時間は1日と48分です。月の軌道は季節によって異なります。また48分というのは概算にすぎません。実際の月の出の遅れは、28分から78分まで変化するようです。