公開中

順次公開予定

9.バビロニア小数のしくみ｜60進法の記数法と小数表現を探る

『バビロニアの数』は全17記事からなるWeb連載です。

前回の記事はこちら 8.小数の歴史 | バビロニア人は小数を知っていた？有限小数とは？

前回のお話〔8.バビロニアの小数〕で述べたように、バビロニア人は1より小さい数としての小数という概念を持っていました。バビロニアの60進小数とはどのようなものだったのでしょうか？

ページ目次

1 60進数の記数法
2 60進数⇄10進数の変換
3 分数を d進小数に
- 3.1 1/7を10進小数で表す
- 3.2 1/7を60進小数で表す
4 10進小数⇄60進小数の変換
5 60進数の標準的な表記法

60進数の記数法

いろいろな記数法

60進数の記数法にもいろいろなものがあります。本連載でもすでに、絵文字による方法、楔形数字による方法と、算用数字と漢数字による方法を述べました。今回、また別の記数法を導入します。実は60進法の記数法としては標準的なものがあり、他の著作ではよく使われているのですが、以下で使う記数法はそれとは違う本連載独自の表記法です。標準的な記数法については最後に述べます。

60進数とは、0～59 までの数を並べたものです。以下の表に60進数の4つの記数法を示します。絵文字、楔形文字、〔 7. 60進数の掛け算〕で述べたこれまでの記数法、今回新しく導入するこれからの記数法の4つです。これらは記数法が違うだけで同じ数を表しています。

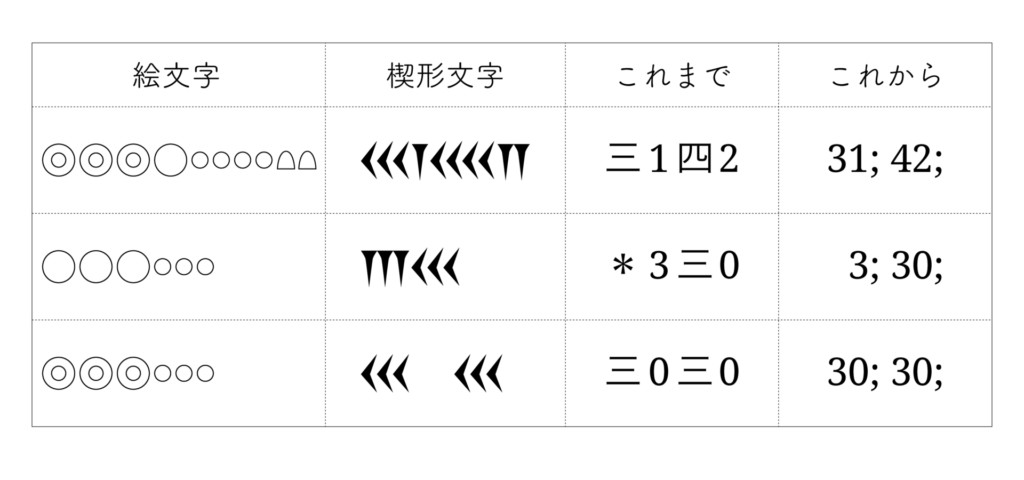
列見出し（左から右）：絵文字／楔形文字／これまで／これから 1行目（上段）： • 絵文字：同心円4つ、小円3つ、三角2つ • 楔形文字：左向きのくさび型8つ（←←←←←←←←） • これまで：三 1 四 2（漢数字） • これから：31; 42; 2行目（中段）： • 絵文字：大きな円3つ、小さな円2つ • 楔形文字：上向きのくさび3つ、左向きのくさび3つ（↑↑↑←←←） • これまで：＊ 3 三 0（アスタリスク付き） • これから：3; 30; 3行目（下段）： • 絵文字：同心円2つ、大中小の円が計3つ • 楔形文字：左向きのくさび2つ、右向きのくさび2つ（←←→→） • これまで：三 0 三 0（漢数字） • これから：30; 30;

これから用いる60進の記数法では、数字を区切り記号 “ ; ” (セミコロン) で区切って表します。小数の場合は途中で小数点を挿入します。

関連記事以下の記事で詳しく解説しています。

7. 60進数の掛け算 | 楔形文字の進化とバビロニアの記数法

60進小数の定義

60進小数は正確には次で定義されます。a_n, a_n-1, …, a₁, a₀, b₁, …, b_m を自然数とします。このとき

は、次の数を表します。

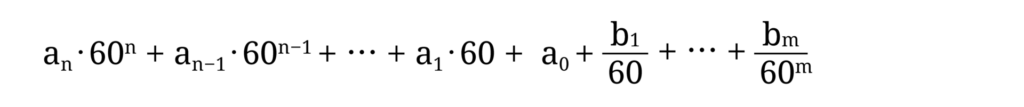
aₙ・60ⁿ + aₙ₋₁・60ⁿ⁻¹ + ⋯ + a₁・60 + a₀ + b₁／60 + ⋯ + bₘ／60ᵐ

一般には、各 a_i, b_i は次を満たします。

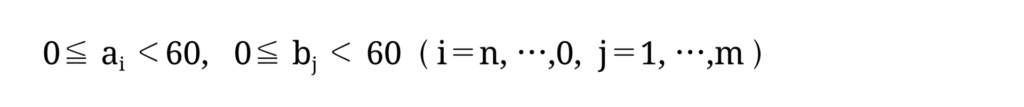
0 ≦ aᵢ < 60，0 ≦ bⱼ < 60（i = n, ⋯, 0，j = 1, ⋯, m）

しかし、計算の途中で（桁上がりなどで）この条件を満たさないものが現れるので、この条件は特に課さないこととしました。

各々の数字は10進数で表します。つまりセミコロンで区切られた2桁の10進数が60進数の一つの数字です。したがって、60進数の1桁の数は、10進数と同じとなります。たとえば 60進数で 54; と書いても、10進数で 54 と書いても同じ自然数を表します。60進小数で、整数部と小数部が共に1桁の場合、たとえば 12.34; の場合、最後にセミコロン ; がないと10進小数と解釈されてしまいますから最後に必ずセミコロンをつけます。

時間、角度の表し方はバビロニア由来

現在私たちが使っている、1日24時間、1時間60分、1分60秒という時間の表し方、あるいは、円ひとまわりの角度が 360度という角度の表し方もバビロニア数学から来ています。英語の分 (minute) はラテン語の「小さいもの」minuta(ミヌタ)から、英語の秒 (second) はラテン語の「もっと小さいもの」secunda minuta (セクンダ•ミヌタ)から来ています。

日本語と中国語の「分」は 1/60 以外に 1/10 の意味もあります。1/10 の意味の「分」は日本に入ってきてからしばらくして「割」に代わりました。「五分(ごぶ)五分(ごぶ)」という場合の「五分」は 5/10 の意味です。

60進数⇄10進数の変換

60進数を10進数に変換する

〔 5. 記数法の変換〕で、イギリスの貨幣を最下位の単位ファージングに変換する方法を述べました。量表現は「位(くらい)名方式」と本質的には同じです。60進数の 60³, 60², 60, 1 などは位名で、60進数 a;b;c;d; は定義より、数

を表します。関数電卓で計算するときは次のように変形すると簡単です。

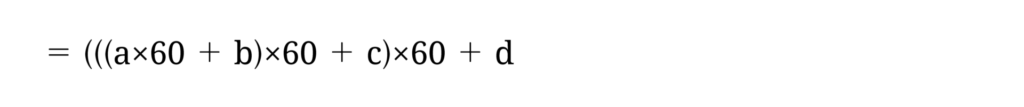
たとえば 60進数 12;34;56; を 10進数に直してみましょう。

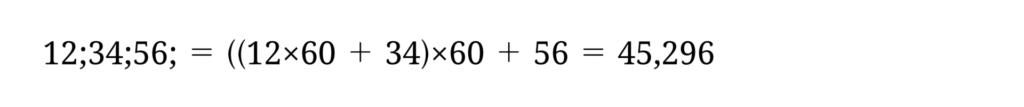
12;34;56; ＝ ((12×60 ＋ 34)×60 ＋ 56 ＝ 45,296

10進数を60進数に変換する

イギリスの貨幣のファージング硬貨を「最簡形」に変換する方法と同じです。45,296 を 60進数に直しましょう。

45296 ÷ 60 = 754 余り 56 754 ÷ 60 = 12 余り 34

よって、（ 割り算の原理 を思い出してください〔5. 記数法の変換〕参照）

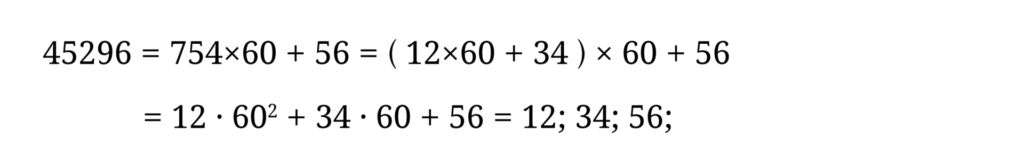
となります。

関連記事以下の記事で詳しく解説しています。

5. 記数法の変換 | 時間・分・秒を最小の単位「秒」で表してみよう

剰余計算。割り算の余りを求めるには？

〔5. 記数法の変換〕で自然数 a と b に対し、「a ÷ b ＝ q 余り r」という計算をしました。このように、商 qと余り r を求める計算を剰余計算といいます。たいていの関数電卓はこの機能 [ mod ] を持っていますが、持っていない電卓では次のように計算してください。45296 ÷ 60を計算しましょう。45296 を 60 で割ると

45296 ÷ 60 ＝ 754.9333…

となります。この結果から整数部の 754 を引いて、その結果に 60 を掛けると

0.9333… × 60 ＝ 56

となり、余りの 56 が得られます。電卓によっては 55.99999… となることもありますがこうなった場合も答えは 56 です。

上では自然数の10進数を60進数に、60進数を10進数に変換する方法について述べました。60進数について述べましたが、実は 60進数に限らず任意の d進数でも同じ方法で計算できます。

分数を d進小数に

次に小数について考えましょう。自然数については上で述べましたから、以下では 1より小さい数を扱います。

1/7を10進小数で表す

まず 1/7 を d進小数で表すことを考えます。dは何であっても同じですから、d＝10 で説明します。10進小数の場合は電卓を使って1÷7を計算すれば 0.14285714… と答えが出ます。これを 10倍すると 1.4285714… となり、整数部に第1桁目の 1 がきます。1 を取ってまた 10倍すると 4.285714… と2桁目の 4 がきます。これをつづけると小数部が1桁ずつ整数部に上がってきます。ここでは 1/7 を小数展開した形で表しましたが、この操作を分数のまま次のように変形することができます。

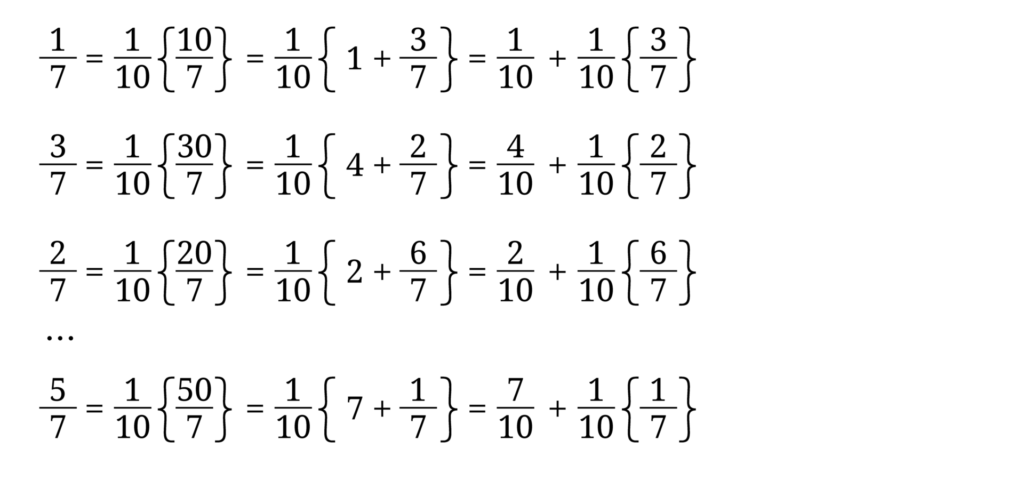
\frac{1}{7} = \frac{1}{10} + \frac{4}{10^2} + \frac{2}{10^3} + \frac{8}{10^4} + \frac{5}{10^5} + \frac{7}{10^6} + \frac{1}{10^7} \left\{ \frac{1}{7} \right\}

最後に 1/7 が現れましたから、後はこの繰り返しとなります。

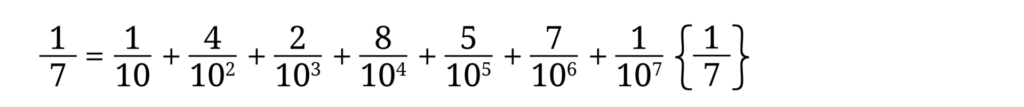
よって、

分数 \frac{1}{7} は、循環小数として \frac{1}{7} = 0.\overline{142857}

となります。

1/7を60進小数で表す

60進小数の場合も同様です。

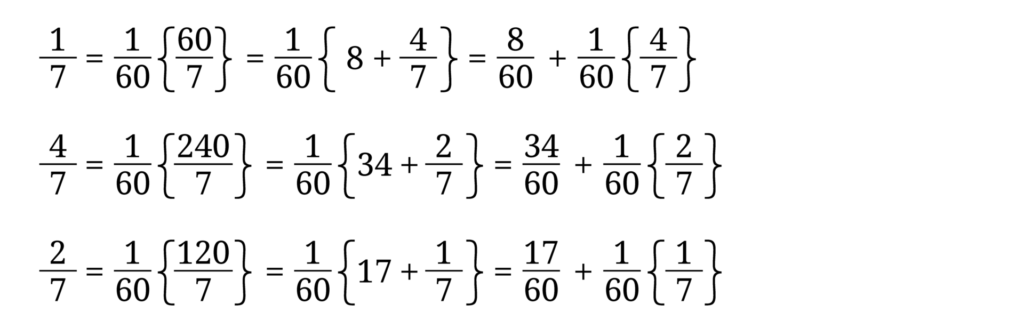
\frac{1}{7} = \frac{1}{60} \left\{ \frac{60}{7} \right\} = \frac{1}{60} \left\{ 8 + \frac{4}{7} \right\} = \frac{8}{60} + \frac{1}{60} \left\{ \frac{4}{7} \right\} \frac{4}{7} = \frac{1}{60} \left\{ \frac{240}{7} \right\} = \frac{1}{60} \left\{ 34 + \frac{2}{7} \right\} = \frac{34}{60} + \frac{1}{60} \left\{ \frac{2}{7} \right\} \frac{2}{7} = \frac{1}{60} \left\{ \frac{120}{7} \right\} = \frac{1}{60} \left\{ 17 + \frac{1}{7} \right\} = \frac{17}{60} + \frac{1}{60} \left\{ \frac{1}{7} \right\}

となり、最後に 1/7 が現れたので、あとはこの繰り返しです。1/7 は60進の循環小数となります。

分数 \frac{1}{7} は、10進数で循環小数として \frac{1}{7} = 0.\overline{142857}

10進小数⇄60進小数の変換

10進小数を60進小数に

次に 0.142857142857(≒1/7) を「60倍して整数部を取る」という方法を繰り返してみましょう。60進の4桁で打ち切ります。

0.142857142857 × 60 = 8.571428571
0.571428571 × 60 = 34.28571426 0.28571426 × 60 = 17.1428556 0.1428556 × 60 = 8.571336

したがって

となります。これより次の 60進小数が得られます。

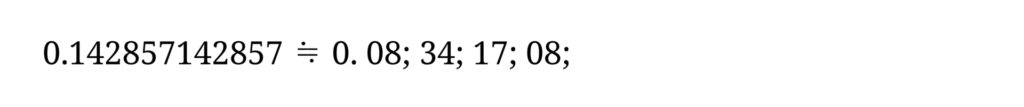
60進小数を10進小数に

60進小数 a;b;c;d; を10進小数に直すには次の定義式を使います。

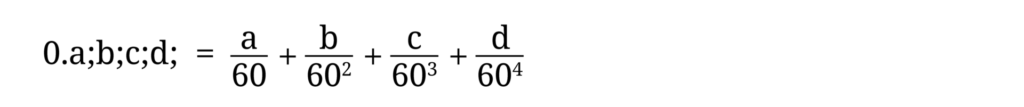
0.a;b;c;d; = a/60 + b/60² + c/60³ + d/60⁴

0.08;34;17;08; を10進小数に変換しましょう

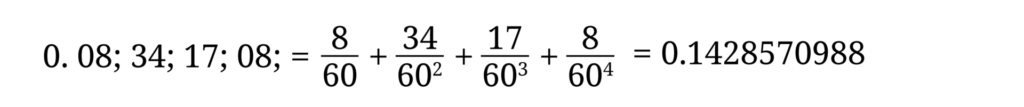
0.08;34;17;08; = 8/60 + 34/60² + 17/60³ + 8/60⁴ = 0.1428570988

となり、上の 1/7 の小数展開とほぼ一致します。

角度と時間

現在でも角度と時間は60進です。〔 5. 記数法の変換〕では、最小単位の秒に変換しましたが、通常は“度”と“時間”が基準単位です。つまり通常は次のように“度”と“時間”のところに小数点があるものとしています。

35度25分45秒は 35.25;45; 度と表記される。 10時間32分11秒は 10.32;11; 時間と表記される。

小数点以下を10進小数に変換してみましょう。

度分秒や時分秒の表記を小数に変換する式の例。上段では 35 度 25 分 45 秒を、35 + 25/60 + 45/3600 により 35.42916667 度と換算。下段では 10 時間 32 分 11 秒を、10 + 32/60 + 11/3600 により 10.53638889 時間と換算している。

上の計算は関数電卓で計算し、小数点以下適当なところで四捨五入しています。したがって、厳密には、＝は等号ではなく近似的に等しいことを表しています。

こんどは逆に上の10進小数を60進小数に変換してみましょう。

小数を度・分・秒または時間・分・秒に変換する例。上段では 0.42916667 度を 25.7500002（分）、0.75×60=45（秒）と変換し、35.42916667 度 = 35 度 25 分 45 秒と表現。下段では 0.53638889 時間を 32.183334（分）、0.183334×60 = 11.0004（秒）と変換し、10.53638889 時間 = 10 時間 32 分 11 秒と表現している。

となり、もとに戻りました。

60進数の標準的な表記法

本連載で用いている60進数や 60進小数の表記法は、本連載だけの表記法で、バビロニア数学に関する他の著作ではこれとは別の表記方法が採られています。その表記法は、すでに広く使われていて、標準的な表記法となっています。その表記法では、小数点はセミコロン “;” で表し、2つの60進数の数字を区切る区切り記号は、コンマ “,” を用います。

本連載では上で述べたように、小数点は10進法や2進法と同じピリオド “.” を、数と数の区切り記号としてはセミコロン “;” を用いることにします。コンマは文章の句読点(くとうてん)として用いられ、数学でもメタ記号としてよく用いられるからです。標準的な表現に慣れた読者は混乱するかもしれませんがご了承ください。