8.バビロニアの小数

バビロニア数学の驚異：小数の概念と平方根計算

バビロニア人は小数を知っていた！？

バビロニア数学の驚くべきところは、この時代にすでに小数の概念を持っていたことです。粘土板に 小数点 を表記することはしませんでしたが、1より小さい数としての小数という概念を持っていました。それどころかこの小数を使って、平方根（例えば √2）の計算まで行っていたのです。

この小数という概念を獲得するのに、おそらく計算盤が役に立ったのだと思います。中国の計算盤は、古くは現在のソロバンではなく、マス目に区切られた板の上に算木と呼ばれる棒を置くものでしたが、原理は現在のソロバンと同じです。紀元前のだいぶ前から10進法が使われており、九九も使われていました。計算盤を用いると、数という概念が具体的な対象として頭の中で形作られます。「一の位」の左のマス目は「十の位」、「十の位」の左のマス目は「百の位」…、では「一の位」の右のマス目は何だ？このようにして中国でも小数の概念が得られていました。

日本・中国の記数法

〔 3.位取り方式 〕で述べた日本の記数法を復習しましょう。これは中国から来たものですが大きな数を表すにはとても便利な方法です。ソロバンの各桁には次の位名が割り当てられます。

ここで、10^-n は 1/10ⁿ を表します。すなわち次を表します。

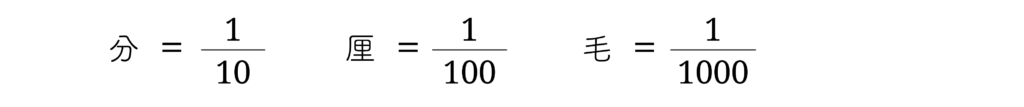
もちろん 10ⁿ や 10^-n などの記法は現在のものです。

ヨーロッパでは、近世になるまで小数や分数を知りませんでした。しかし中国ではすでに紀元前から小数の概念を持っていたのです。1より小さい数は次のように表します。

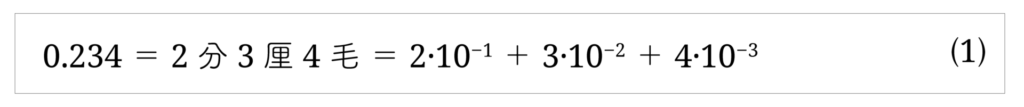
“分”は中国から日本に入ってきて“割”に変わりました。分は60進法（時間とか角度）だと 1/60 を表します。したがって、1/10 の場合は“割”とした方がよいかもしれません。

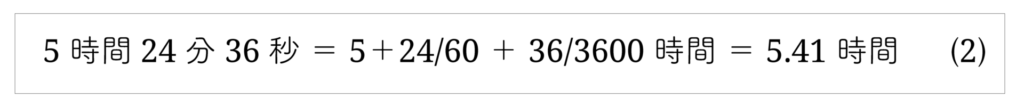
〔 5. 記数法の変換 〕では、上のような表現を 単進表現 として最下位の秒の単位で表しました。しかし上の場合は “時間”を基準単位としています。この“分”と“秒”は単位名と見ることができますが、あとで見るように時間や角度の場合は 60進数の位名とみる方が自然です。

式 (1) や (2) が示すように、「位名方式」とか「量表現」があれば、実用上は「小数」は必要ないのです。たとえば日本の貨幣でいえば、1円という最小単位で間に合わなければ、“銭”とか“厘”というもっと小さい単位を考えればよいからです。さらにいうと、実用上は「分数」か「小数」のどちらか一方があれば、他方は必要ありません。実際、現在の日本では分数は日常生活から姿を消しています。しかし分数も現代数学では依然としてとても大切な概念です。

有理数とは何か

有限小数と無限小数

ここで、有理数の復習をしておきましょう。有理数とは、 分母と分子が共に整数の分数で表される数 のことです。整数、分数、有理数などは「数が何進数で表されているか」とは関係のない概念です。しかし以下で述べる「有限小数」とか「無限小数」などは、数の表現に関する概念なので、何進法かに関係します。 　

まず 10進数について考えます。小数部が有限で終わっている小数を有限小数、小数部が無限に続くものを無限小数といいます。a と b が共に整数の分数 a/b を小数に直すには、a を b で割ればよいのです。5/22 でやってみましょう。

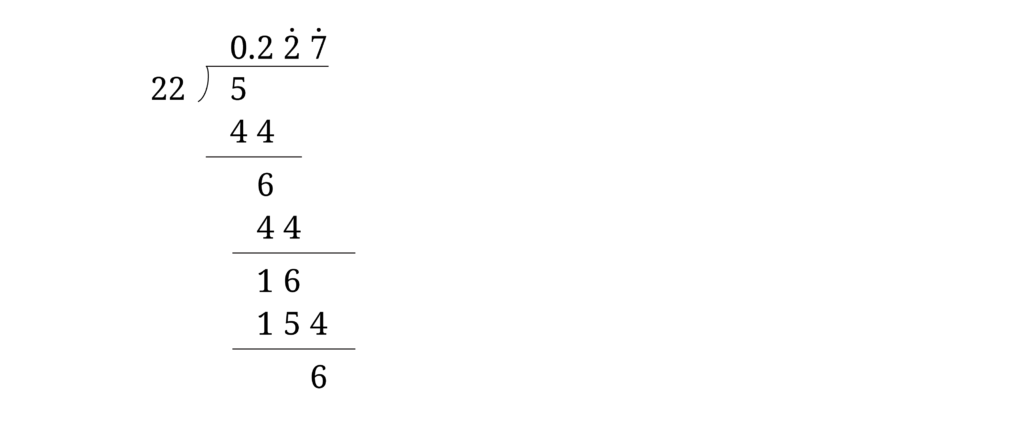
50 を22 で割ると、商が 2 で余りが 6、60 を 22 で割ると、商が2 で余りが16、160 を 22 で割ると商が7 で余りが 6 となります。最後の余り 6 は以前に現れています。これからあとは繰り返しとなり、答えは 0.2272727 … となります。繰り返される 27 を循環節といい、節の始まりと終わりの数の上に黒丸を打って以下のように表します。このような小数を循環小数といいます。

一般に b で割る場合、余りは 0 から b – 1 までのどれかです。0 の場合は割り切れて、有限小数となります。0 以外の場合は、÷b を続けるうちに同じ余りが出てきます。同じ余りになったら、それ以後は同じ計算の繰り返しです。したがって循環小数となります。有理数を小数で表した時、割り切れない場合は循環小数になるのです。

循環小数は分数で表される

今度は、 循環小数は分数で表される ことを示しましょう。

を考えましょう。

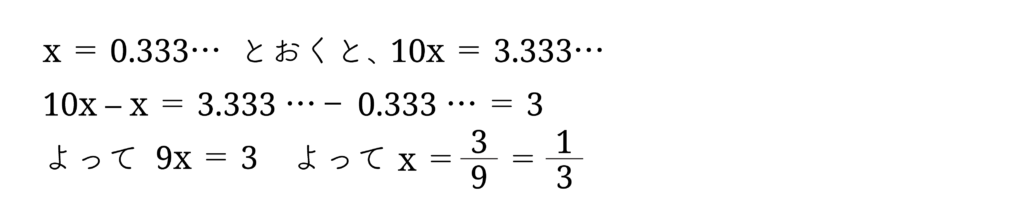
となります。次にもう少し一般的な例を考えてみましょう。

を考えます。これは、最初の循環しない部分と循環節を切り分けて、

となり、循環節は分数で表されます。したがって a 全体も

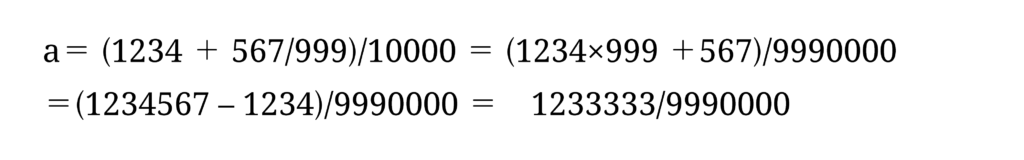
となり、分数で表せます。

以上の議論より、「有理数 ＝ 有限小数＋循環小数」であることが分かりました。したがって、「無理数 ＝ 循環小数以外の無限小数」となります。現代人なら、循環小数を受け入れられますが、バビロニア人は循環小数を“数”として認めることはしませんでした。

有限小数を分数で表す：分母は2,5以外の素因数を持たない

ここでもう少し用語の復習をしておきましょう。a, b, c を自然数とします。a＝b·c とかけるとき、a は b の約数、または因数といいます。任意の自然数 a に対し a ＝ 1·a ですから、1 は任意の自然数 a の約数であり、a は a の約数です。1 と自分自身以外に約数を持たない数を素数といいます。素数である因数を素因数といいます。自然数 a と b が、1以外の共通の約数を持たないとき、a と b は互いに素である、あるいは既約であるといいます。
数学では同じ概念を違う表現で表すことがよくあります。「約数」と「因数」、「互いに素」と「既約」もこの例で、どちらかに統一した方がよいように思いますが、そうはいかないようです。

本連載で扱う分数は、分子も分母も自然数の分数です。また、分母と分子は互いに既約であるとします。上では、任意の分数は有限小数か、循環小数となることを示しました。では分数 a/b が有限小数となるのはどんな場合でしょうか。たとえば有限小数 0.12345 は

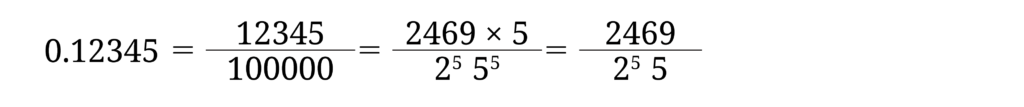
となり、分母が 2ⁿ5^m の形の分数で表されます。逆に分母が 2ⁱ5^j の形の分数は、たとえば i＝3, j＝1 のとき

となり、有限小数で表されます。一般に次が成立します。

 a/bが有限小数  ⇔  b が 2 と 5以外の素因数を持たない

分数と小数の関係

整数と分数の和を表す記法として帯分数というものがあります。たとえば 17/5 は  3 ⅖と表せます。しかしこの記法は掛け算  3 × 2/5と紛(まぎ)らわしいし、分数が1個しか書けません。したがって本連載ではこれを 3;2/5 と書くことにします。

もう一度イギリスの貨幣単位を考えます。

1ポンド＝20シリング、1シリング＝12ペンス、1ペニー＝4ファージング

小数とか分数の概念がないと、ファージングより小さい金額は扱えませんが、そんな必要はなかったのでしょう。もし必要なら、ファージングより小さい貨幣単位（たとえは 1/10ファージングにあたる貨幣単位）を作ればよいのです。しかし、ポンドを基準単位として見たい時があります。

中世（13世紀）のアラビアの数学はヨーロッパより格段に進んでいました。ヨーロッパの数学者フィボナッチ※は、アラビア数学をヨーロッパに紹介しています。彼はアラビア数字 0, 1, 2, …, 9 とその計算法を紹介したことで有名ですが、分数や小数も紹介しています。たとえば、1ポンド3シリング8ペンス3ファージングをポンドで表すと次のようになります。

これは「アラビア式分数」と呼ばれていたようでしたが定着しなかったようです。古代中国では上で述べたような位名を持っていましたから、たとえば 3.1415926 は

と表すことができます。つまり、中国ではすでに紀元前に、実質的に“小数”の概念を持っていたのです。

今回のお話では10進数について議論をしてきました。しかし本連載の主な対象は 60進数です。これについては第9回〔 60進小数 〕で議論しましょう。