4. 60進法の起源 バビロニア | シュメール人が発明した記数法

シュメール人の発明：位取り方式とその起源

現在私たちが使っている 10進数は、前回のお話で述べた 位取り方式と呼ばれる画期的な記数法です。この10進数はインドで生まれ、アラビアに伝えられ、やがて12世紀にヨーロッパに伝えられます。しかしヨーロッパでは長い間この記数法は定着しませんでした。15世紀になると、イタリアを中心に少しずつ普及し始めます。「17世紀の科学革命は10進数がなければ成し遂げられなかった」と言われるぐらいこの記数法は評価されています。この記数法では記号の “0” が重要な働きをしますから、「 0の発見 」としても有名です。しかし、位取り記数法はインドよりもずっと前にバビロニアで発見されているのです。ただし、バビロニアの記数法は10進数ではなく60進数でした。

60進数の書かれた楔形文字の粘土板文書は、メソポタミアの遺跡に埋もれ長い間忘れさられていました。したがって、位取り方式がシュメール人の発明だということを誰も気づきませんでした。しかし、60進数は延々と歴史の中を生き延び、現在まで伝わっていたのです。時間や角度の「分」や「秒」はバビロニアのから伝わったものだったのです。

ではどのようにして60進数という記数法が生まれたのか、その出生の秘密を探ってみましょう。

計算に使われたトークンとは？

図4.1 にあるように、古代では数えるものによっていろいろな形の計算玉(トークン)が用いられていました。たとえばヒツジは丸い円盤に十の字の書かれた計算玉(トークン)でした。

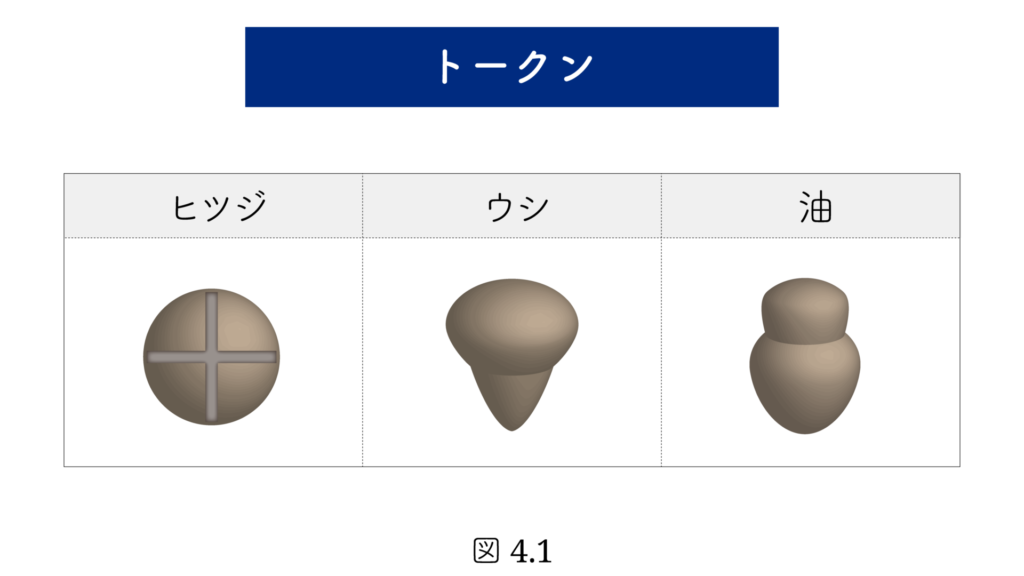
計算玉は計算にも用いられましたが、封泥(ブッラ)と呼ばれる粘土の壺に入れられ、個数を記録するのに用いられました。やがて、計算玉は絵文字で表されるようになります。ヒツジは丸に十の字の記号 十 となりました。羊3匹は

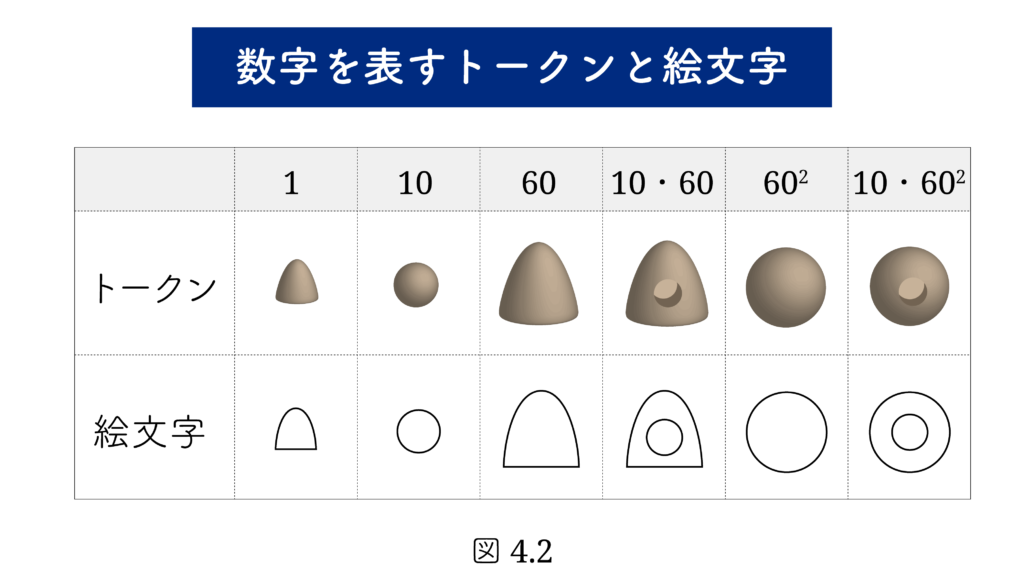
と表します。長い年月が経つうちに、ヒツジを数えるのもウシを数えるのも同じ計算玉でいいのではないかと気づきます。おそらく数えるものの数が増えてきたからでしょう。ここで“数”と数えるものの分離が起きます。しだいに数を表す専用の計算玉が考え出されました。図4.2 に示すように、小さなドングリのような形をした計算玉（ 小ドングリ ）は 「1」、小さな球形の計算玉 ( 小玉 ) は 「10」、大きなドングリ形の計算玉 ( ドングリ )は 「60」を表します。大きなドングリ形に円形を押しつけたもの( 穴付きドングリ )は 「10×60 」、大きな球形 ( 大玉 )は「60²」、大きな球形に円形を押しつけたもの ( 穴付き大玉 )は「10·60²」を表します。これらの計算玉は 図4.2 のような絵文字で表されました。

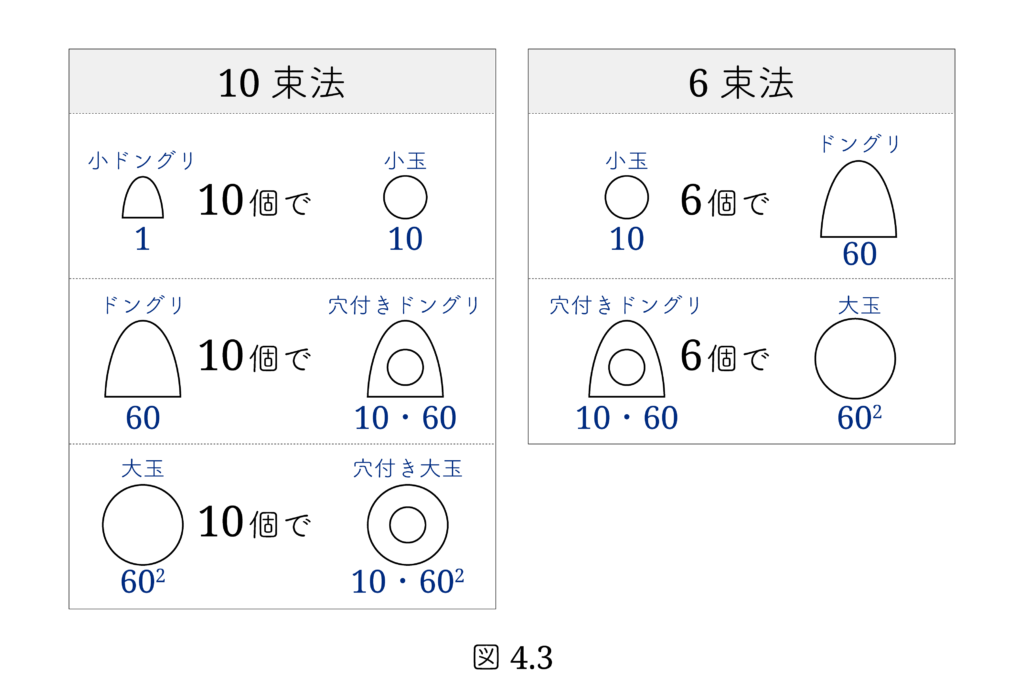
これらの計算玉はこれまで 60進数と考えられてきましたが、 図4.3 のような 10束法と6束法の複合体系 と見ることができます。

計算の仕方（特に連載の後半で述べる掛け算）を見ると、バビロニアの数体系は純然たる 60進法と微妙に異なるのです。これを 6・10進法 と呼ぶことにします。以下ではこれについて詳しく見てみましょう。

60進法の考え方「6・10進法」の解釈

60進法とみる従来の見方では、小玉と小ドングリを組にしてひとつの数字を表し、同様に穴付きドングリとドングリ、穴付き大玉と大玉をそれぞれ組にして数字を表すと考えます。すると、小玉と小ドングリで1から59までの数、穴付きドングリとドングリで60から59・60までの数、穴付き大玉と大玉で59・60²までの数を表すことができます。

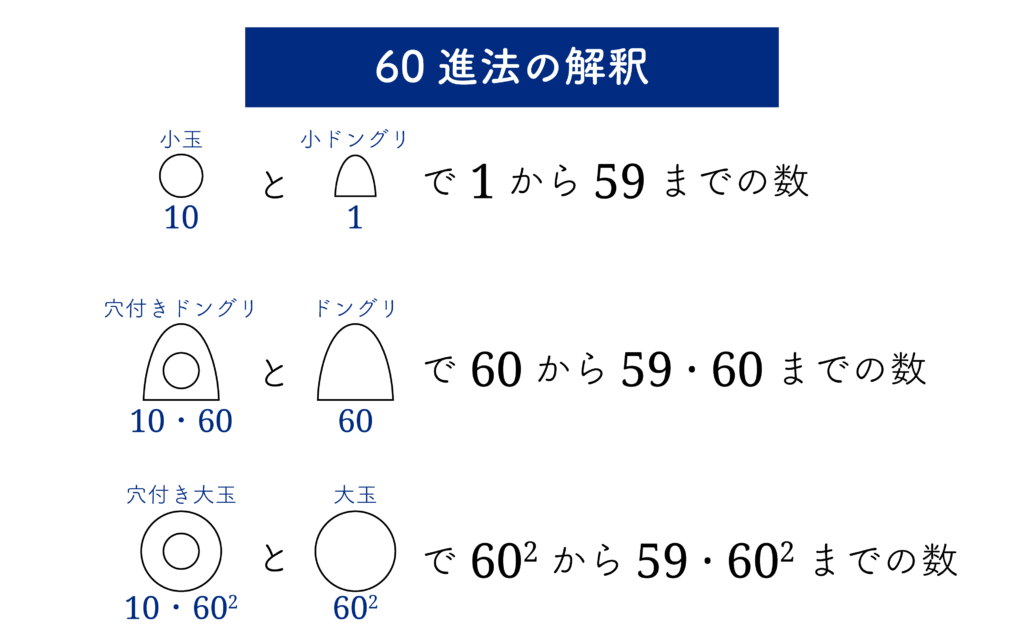
たとえば、

は、以下のように表すことができます。

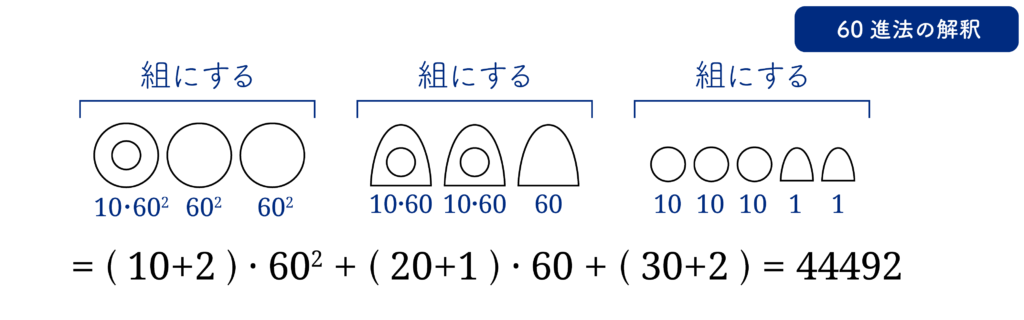
このようにみると60進数ですが、このように組にせず、10束法と6束法の組み合わせとみることができます。これが 6·10進法の解釈です。この解釈で計算すると、

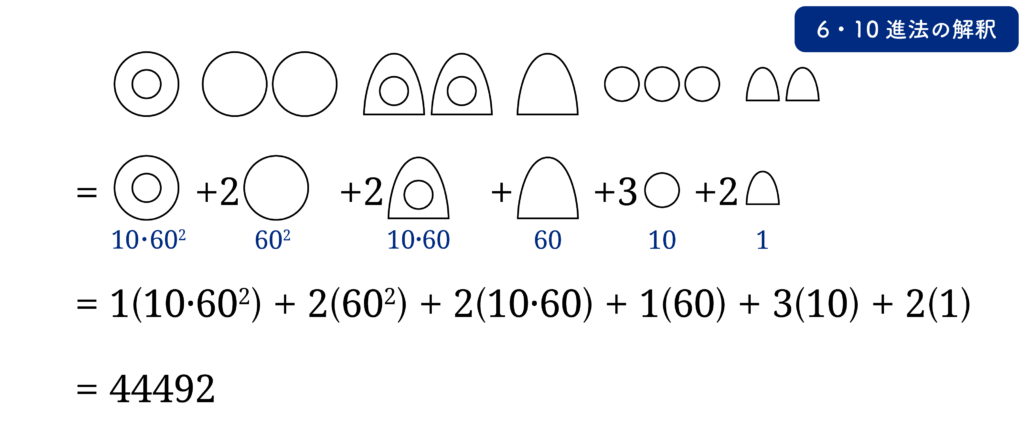
となります。6·10進法の考え方を使って、実際に足し算をやってみましょう。（ 図4.4 ）

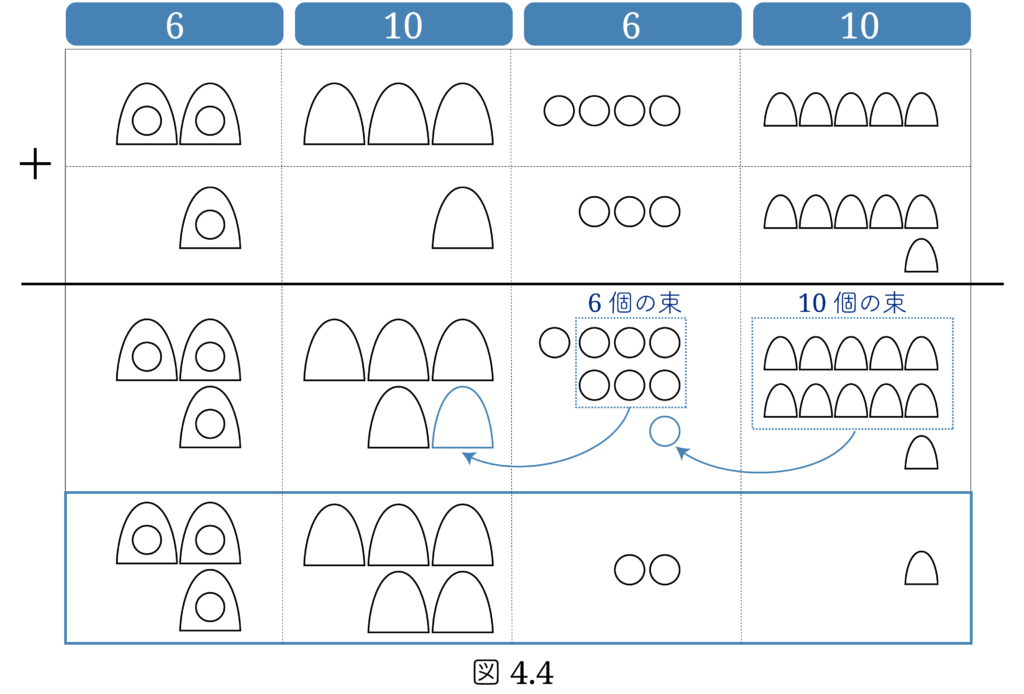
まず、一番下の桁の 小ドングリ を加えます。11個ですから、10個の束ができ、桁あがりが生じます。次の 小玉は桁あがりと合わせて 8 となります。この桁は6個で束ができ、桁あがりが生じます。

このように計算を行なえば、10進数とほとんど同じ手間(てま)で計算ができます。したがって、これは60進数というよりは 6•10進数と読んだほうがよいと思います。足し算は簡単ですが、問題は掛け算です。シュメール人は 60×60 の掛け算表を使って掛け算を計算したのでしょうか。これについては連載の後半の回で考えることにしましょう。

位取り方式はどのように発達したか

上では筆算で計算しましたが、シュメールでは地面に計算玉を置いて計算していたと思います。あるいは計算盤(アバクス)が使われていたかもしれません。

このとき、計算玉の置かれる位置は、小ドングリは一番右、小玉 は 小ドングリのすぐ左、ドングリはその左…というように、種類によって決まっていました。この位置のことを「位(くらい)」と言います。1の位、10の位(くらい)、60の位、600の位、3600の位、… と位によって置く計算玉が決まっていたのです。計算玉には種類があるので、別に置く位置を決める必要ななかったのですが、桁数の大きい計算を何度もするうちに、位の順に計算玉を並べた方が計算が効率的で間違いも少なくなることに気がついたのでしょう。すると粘土板に書くときも大きい位から小さい位に、左から右へと決まっていきます（粘土板によっては上から下に並んでいるものもあります）。

絵文字では、”1″ を表す計算玉 小ドングリ と、”60″を表す計算玉 ドングリ は大きさが違うだけですが、時代が経つにつれ、この2つの区別がつかないものが現れるようになります。現れる位置によって両者の区別がつくのですから、読み間違えることはありません。楔形文字に移行し時代とともに発展すると、この位による文字の区別は完全になくなります。このように、違う位に同じ数字を用いる記数法を位取り方式といいます。たとえば10進法の 333 では、一番左の3 は三百、二番目の 3 は三十、一番右の 3 は三と、現れる位置によって表す数値が違いますが、同じ記号 3 を用いています。つまり、私たちの使っている現在の算用数字は位取り記数法です。（詳しくは〔3.位取り方式〕を参照）

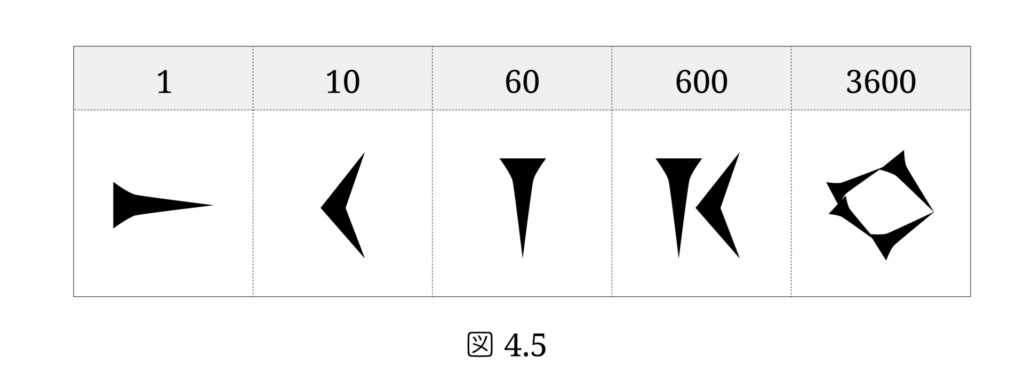
シュメールの絵文字はだんだん楔形文字に移行していきました。60の位や 600の位に対応する楔形文字がありますから、位取り記数法への移行のほうが楔形文字への移行より早いか、同時進行だったようです。図4.5 に示す楔形文字は、1の位と60の位は「横と縦」の違いで区別され、位取り方式ではありません。楔形数字も非位取り方式の時代があったのです。

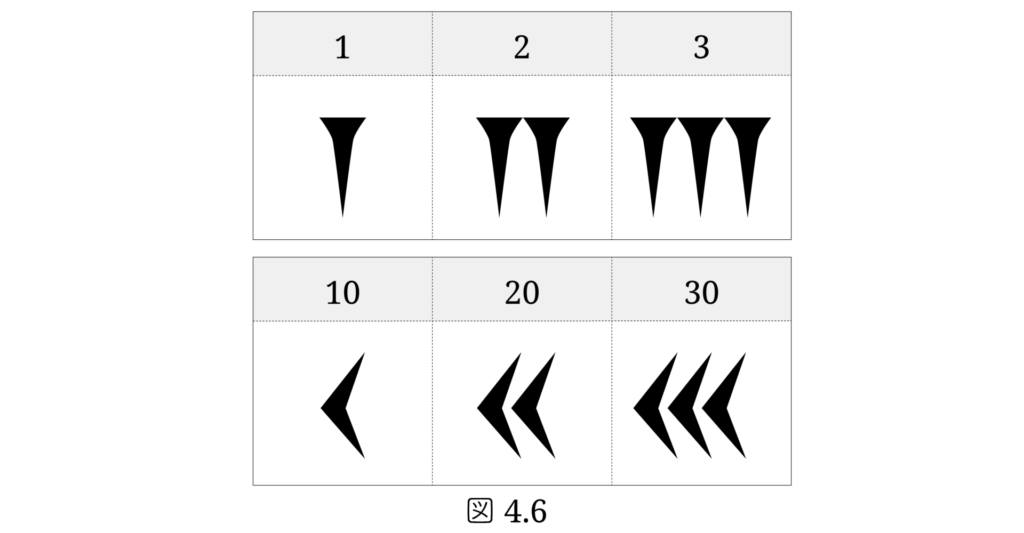
位取り方式の楔形文字は、1の位の数と、10の位の数では別の記号を用います。図4.6 に示すように1の位の数は縦の楔で構成される合成文字、10の位はくの字形の楔で構成される合成文字です。