3.位取り方式

位取り方式とは、数字の表れる位置によって位が定まる記数法のことです。本節ではソロバンや貨幣系を使ってわかりやすく説明します。

日本の記数法：10進数と位取り方式

現在私たちが使っている算用数字 0, 1, 2, …, 9 は、もともとはインドで生まれたようです。それがアラビアに伝わり、アラビアからヨーロッパに伝わりました。したがって、ヨーロッパの人たちはこれをアラビア数字と呼んでいました。しかし、最近ではこれがインド由来であることが認識されるようになり、インド・アラビア数字と呼ぶようになってきましたが、この名称は少し長いので本連載では昔のとおりに「アラビア数字」とか「算用数字」と呼ぶことにします。

本連載ではバビロニアの記数法を扱っていきますが、まず私たち日本人に馴染みのある日本の記数法から見てみましょう。説明のために現代の日本語の記数法を少し変更しています。私たちは、たとえば 321 を 3百2十1 と書くことができます。都合により、3, 2, 1 を漢数字ではなくアラビア数字で書きました。10進数 321 に出てくる3つの数字 3, 2, 1 はそれぞれ「百が3個、十が2個、一が1個」を表しています。このような 一、十、百、… のことを 位くらい名 と呼ぶことにします。次は位名の一部です。

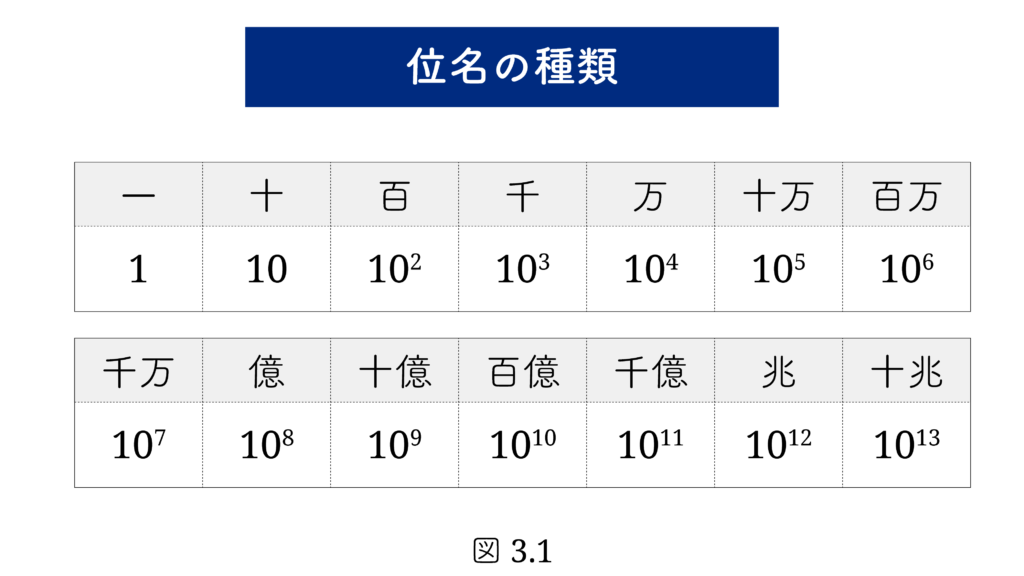
位名と9個の数字 1, 2, 3, …, 9 があれば 位名が存在する範囲のどんな数も表すことができます 。位名をそれぞれを抽象的な数字とみなせば、この位名を使って単一文字方式として数を表すことができます。たとえば「321」は

百百百十十一

と表せます。

数学では任意の対象を示すのに変数を用います。a, b, c を任意の数字とします。3つの数字 a, b, c からなる10進数を abc と書くと、一般には a×b×c と3つの数の積を表すものと取られてしまいます。したがって次のように書くことにします。10進数 abc は  

a百b十c一

と表します。通常最後の“一”は書きませんが、以下ではこれを書くこととします（もちろんこの書き方は一般的ではありません）。一、十、百、… という位名は、図3.1 のように、10⁰, 10¹, 10², … と表すことができます。そこで次のように書くことも許します。10進数 abc は

a10²＋b10¹＋c10⁰

と表します。ここで、10², 10¹, 10⁰ は位名です。

記数法などの表現論では、「表現とそれの表す対象」を厳密に区別します。例えば「123は覚えやすいキーワードだ」と言った場合 123 は3文字の文字列で、数字以外の記号を含むことができますが、「123メートル」といった場合、123 は 123 という文字列が表している数を意味します。しかし、このような厳密な議論は初心者にとって分かりにくいと思うので、上のような表記法を使うことにしました。この表記法を使えば、たとえば 321 の場合、次のように表すと、これが10進数であることと、これがどのような数を表しているのかがはっきりと示されます。

3百2十1一
3・10² + 2・10¹ + 1・10⁰

d進数のソロバンを考える：d 進数の 位名 

d を2以上の自然数とします。ここで d進数の位名方式による表現を定義しますが、これは10進数の 10 を d に置き換えただけです。次をd 進数の 位名 といいます。

d⁰ , d¹ , d² , …

以下ではおのおのの dⁿ をひとつの記号として扱います。 d が10以下の場合は算用数字 0, 1, 2, …, d – 1 で間に合いますが、d が 11 以上の場合は、10, 11, …, d – 1 を表す記号を用意する必要があります。また、数字 0 を使うことに注意してください。a₀, a₁, a₂, … を 0, 1, 2, …, d – 1  のd個の記号のどれかとします。このとき

a_ndⁿ + a_n-1d^n-1 + … + a₁d¹ + a₀d⁰      ( 1 )

を d進数、あるいは d進表現 といいます。ただし以下では最上位の数字 a_n は0ではないものとします。たとえば4桁の10進数 6003 の場合は、n＝3, a₃＝6, a₂＝0, a₁＝0, a₀＝3 ですから

a₃・10³ + a₂・10² + a₁・10¹ + a₀・10⁰
= 6・10³ + 0・10² + 0・10¹ + 3・10⁰
= 6千0百0十3一

となります。また 4桁の2進数 1101 の場合は、n＝3, a₃＝1, a₂＝1, a₁＝0, a₀＝1 ですから

a₃・2³ + a₂・2² + a₁・2¹ + a₀・2⁰
= 1・2³ + 1・2² + 0・2¹ + 1・2⁰
= 8 + 4 + 0 + 1
= 13

となります。

〔たばね法〕ではイギリスの貨幣系を計算する計算盤(アバクス)を考えましたが、ここではソロバンを考えます。ただし各桁には 図3.2で示されるように位名 が書かれています。各桁には d – 1 個の珠があり、0 から d – 1 までの数を表すことができます。

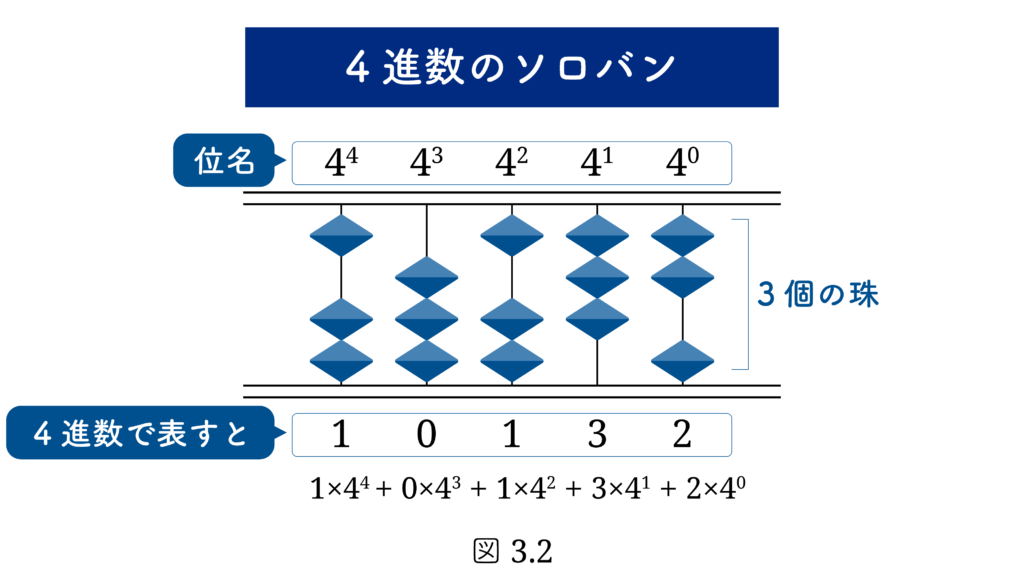
上では d進数を位名付きで ( 1 ) のように表してきました。

a_ndⁿ + a_n-1d^n-1 + … + a₁d¹ + a₀d⁰      ( 1再録 )  

一般には d進数は位名を省略して

a_n a_n-1 … a₁ a₀       ( 2 )

と書かれます。位名を明示しなくても、a_i には位名 dⁱ が付いていることが a_i の位置から分かるからです。言い換えれば、 数字の表れる位置には 位(くらい) が定まっている のです。図3.2ソロバン参照。一番右端が最下位の位で、一つ左に移動するごとに位が一つ上がります。各位には位名が割り当てられていますから、その数字がどのような数値を表すかが分かります。すなわち、( 2 ) の文字列は ( 1 ) の数値を表しています。例えば 321 は「3と2と1」ではなく、「3百と2十と1」を表しているのです。このような記数法を 位取り方式 と呼びます。位取り方式でないものを 非位取り方式 と呼ぶことにします。両者の違いは、非位取り方式では、位ごとに違う数字が用いられることです。 位取り方式は使用する数字の数を少なくすませる画期的な方法 でした。

ここではd進数のソロバンを使って位取り方式について述べましたが、そもそも2進数、10進数とは？なんとなくわかるけど…という方のために簡単な動画を用意しました。数の表し方をイメージできるよう2進数、3進数、4進数のソロバンの珠を動かしています。4進数のソロバンで簡単な足し算もご紹介していますのでぜひご覧ください▼

貨幣系の位名の構造：いくつ束ねると上の位になるか？

〔たばね法〕では、以下のようなイギリスの貨幣系を考えました。

貨幣系は量であって数ではありませんが、ファージング、ペニー、シリング、ポンドも位名と見ることができます。ただし、数の位名（たとえば百）は純粋に数を表しますが、量の場合（たとえばポンド）は数値だけでなく量としての属性（たとえば貨幣という属性）を持ちます。しかし、ファージングが一番下の位で、ペニーが次の位、… といった構造は数の位と同様です。
量の場合、各位は「下の位をいくつ束ねるとその位になるか」が決まっています。この数を 位数(いすう) と呼ぶことにします。例えば、ポンドの位数は20、シリングの位数は12、ペニーの位数は 4 です。数の場合、すべての位の位数は一定で、位数が d なら d進数となります。古代の量では、長さ、重さ、容量、… など種類によって各位名の位数はまちまちでしたが、現代のメートル法では一定の位数となるように定められています。例えば次は現代の重さの単位です。

トン、キログラム、グラム、ミリグラム

これらの位数は 1000 です。

数の発展：ローマ数字とギリシアのアルファベット

ここで「数の発達」を振り返ってみましょう。量のうち個数を表すものが量から“数”として独り立ちします。数は次のように発展します。

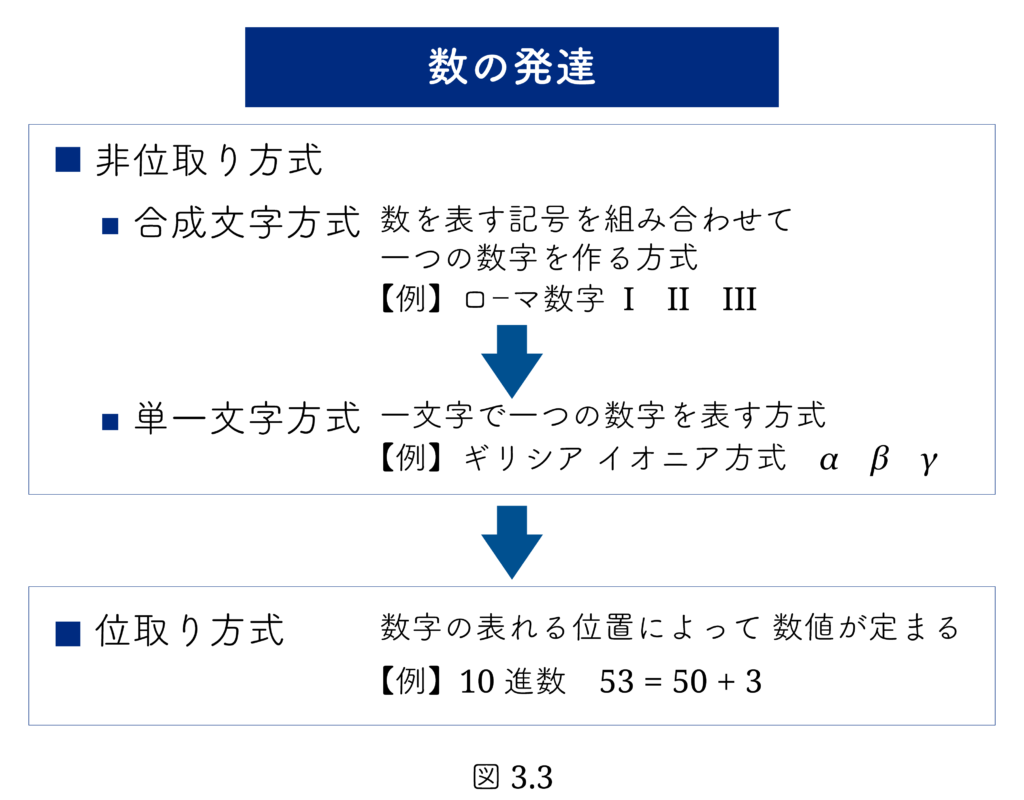
ギリシアの単一文字方式で、「なぜαが1で、βが 2 なのか？」と考えても意味がありません。アルファベットの順に機械的に 1, 2, … と番号を割り当てたにすぎないからです。このような数字の体系を、何もないところから思いつくことはできません。まず合成文字方式の数字体系があって、それを改良したものであると推測できます。また、ギリシアのアルファベットの並び順は、フェニキアのアルファベットの並び順とほとんど同じです。このことからギリシアのアルファベットはフェニキアのアルファベットをまねて生まれたことは明らかです。

ではローマ数字はどうでしょうか。ギリシアのアッティカ方式（合成文字方式）とよく似ていますが、ローマ数字の方が古い形を残しているようです。ローマは多くのものをギリシアから学びましたが、文字や数字もギリシアから学んだのでしょうか。
ローマがまだ寒村のころローマの北にエトルリア人が住んでいました。ローマの初期のころの王はエトルリア人だったようですが、やがてエトルリア人はローマから追い出されます。エトルリア人は謎の民族で、先住民説とオリエントからの移住民説とがあります。当時はイタリア南部にはギリシア人やフェニキア人の植民地ができていて、エトルリアは交易などでギリシア人の影響を受けていました。エトルリア人はギリシア人のような印欧語族ではないようですが、使っている文字はギリシア文字とよく似ています。このことからエトルリア人はギリシア人から文字や数字を学んだという説が有力です。しかしそのころギリシア人はフェニキア人から文字を学んだばかりですし、ギリシアで文字の使用が普及するのはだいぶ後だという説もあります。したがって、エトルリア人が文字や数字の知識を携えてオリエントから移住してきたか、あるいはフェニキア人から学んだという説も成り立ちます。つまり、ギリシアを介さずに伝わった可能性もあるのです。