7. 60進数の掛け算 | 楔形文字の進化とバビロニアの記数法
楔形文字の発達:絵文字から楔形文字への位取り方式の移行
〔 4.バビロニアの60進法 〕で、シュメール人はすでに絵文字の段階で60進数を使っていたことを述べました。 図7.1に示すように、この絵文字の60進数は非位取り方式で、位が違うと使われる絵文字が違っていました。
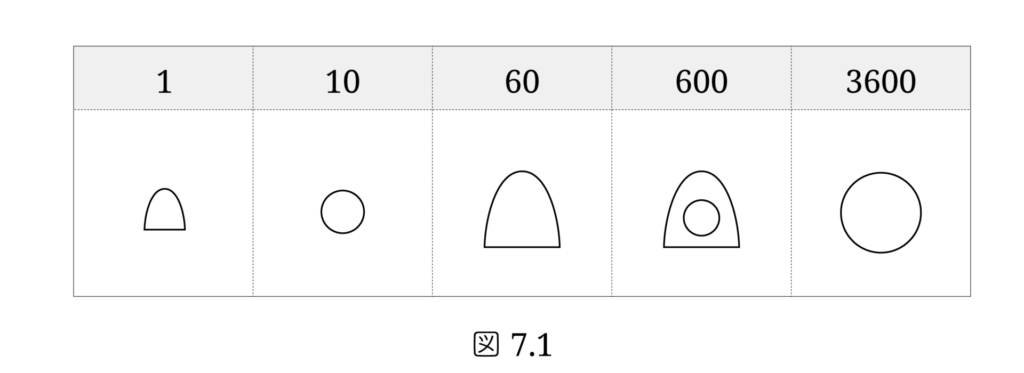
シュメール人は位の位置を決めて数字を書くうちに、位によって記号を変える必要のないことに気がつきます。もともと 1 と 60 は大きさが違うだけでしたが、大きさを区別しなくても 位置でどちらかが判別できる ことに気がついたのです。 位取り方式の発明 です。
次第にシュメール人は粘土板に葦のペンで楔形文字を書き始めます。図7.2 に示す楔形文字では、1, 10, 60, 600, … に対応する楔形文字がそれぞれ存在し、位取り方式ではありません。絵文字が非位取り方式から位取り方式へ移行した時期は、絵文字から楔形文字への移行より早いか、同時進行だったようです。
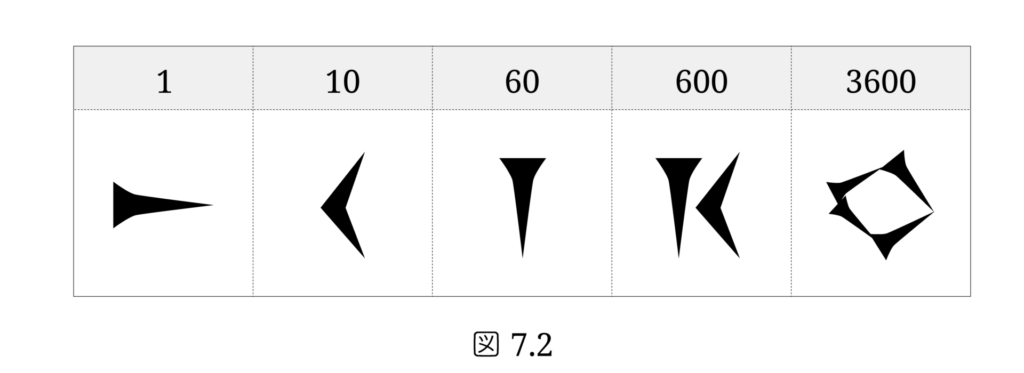
やがて楔形文字の数字は位取り方式となります。しかし各数字は合成文字方式で、1 は 「 | 」で表され、10は「 < 」で表されました。楔形文字の数字は、次の図7.3のように表します。
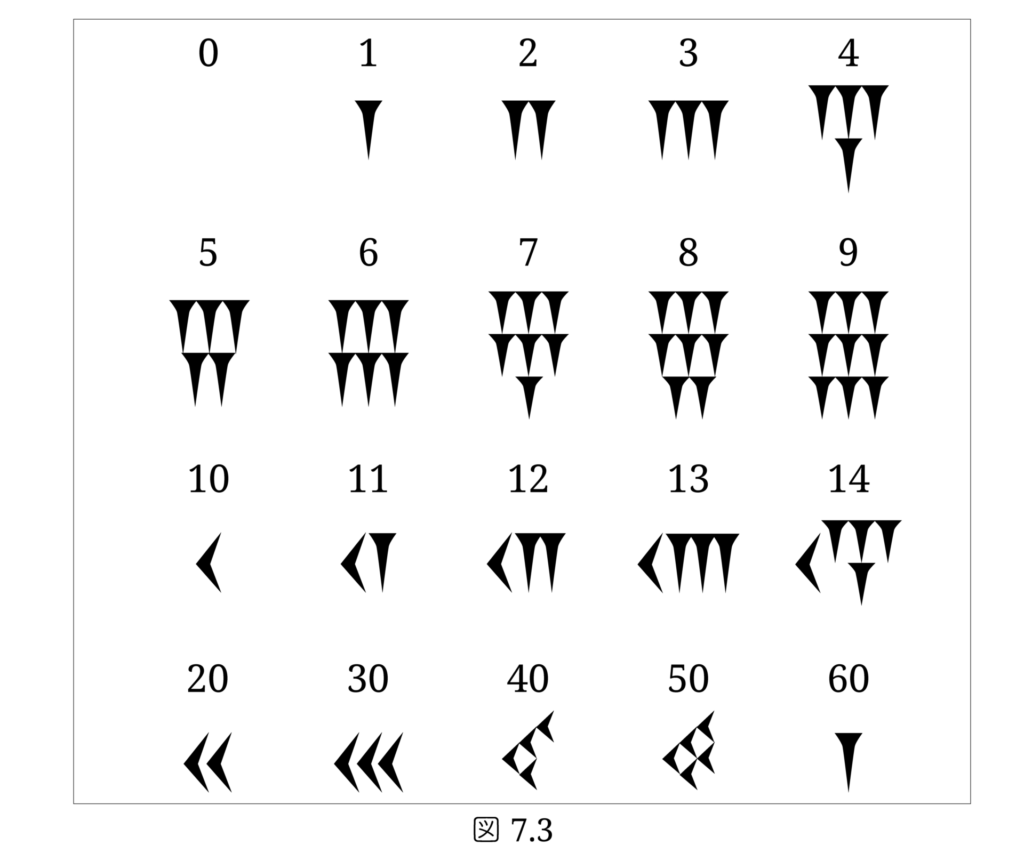
楔形文字と位取り方式:バビロニアの60進数の現代的な独自の記法を考えみよう
楔形数字は、1, 60, 602, … の位は「 | 」で、10, 60·10, 602·10, … の位は「 < 」で示されますから60進数というよりは 6·10進数とみなすことができます。楔形数字は皆さんにとってなじみがないと思いますので、前回のお話でローマ数字を置き換えた時と同様に、現代の文字で置き換えることにします。楔形文字では 空白 が 0 の働きをしていました。前回と同様、1の位の空白を 0 で、10の位の空白を * で表すことにします。 楔形文字の 1 から 9 までを算用数字の 1, 2, …, 9 で、楔形文字の 10, 20, 30, 40, 50 を漢字の 一, 二, 三, 四, 五 と表します( 図7.4 )。
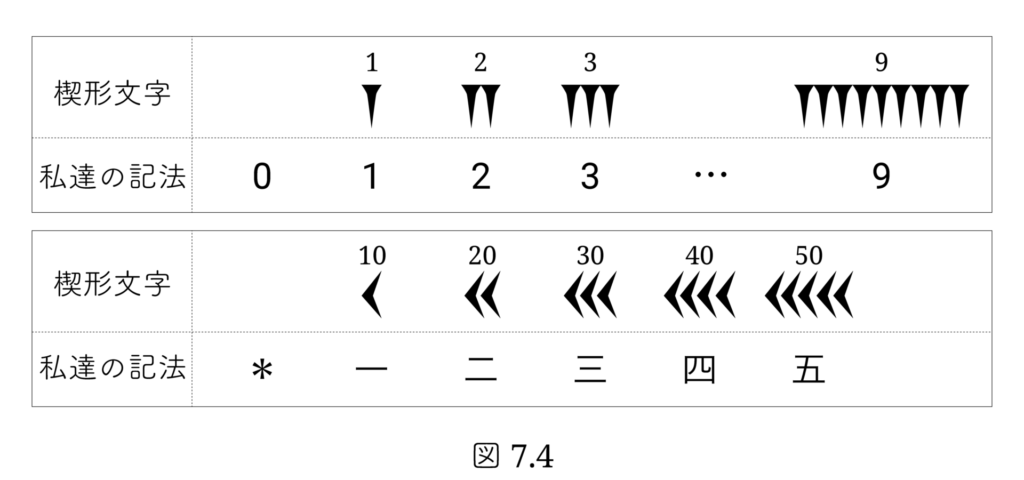
たとえば楔形文字の「 | | | 」は算用数字の「 3 」で、楔形文字の「 < < < 」は漢字の 「 三 」で表すことにします。位取り方式なので、同じ記号でも場所によって値が違います。たとえば

は 6·10進法としての私達の記法では

と書きますが、これは 60進数とみなすと
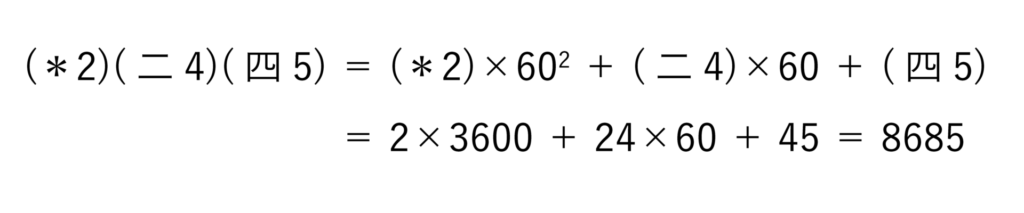
となります。
私達の記法をまとめると図7.5 のようになります。

バビロニアの粘土板に見る6・10進法の掛け算表
バビロニア人が実際に 6·10進法として掛け算を計算した証拠となる粘土板が出土しています。その掛け算表は、59×59 の掛け算表ではなく、a×b の掛け算表で、各 a ごとに1枚の粘土板です。a として 59 個全部が現れているわけではなく、現れているのは次の 22個です。
2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 16, 18,
20, 24, 25, 30, 36, 40, 45, 48, 50
このうち掛け算に使われるのは次の 13個だけです。
2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50
これ以外の数がなぜ掛け算表に現れているかは、連載の後半で説明します。各 a の a×b の粘土板には、上の 13個の b に対し a×b の値が刻まれています。 粘土板の掛け算表を、必要な部分だけ切り取って、上で述べた私たちの記号で書き換えたものが次の表です。( 表7.1 – 表7.3 )
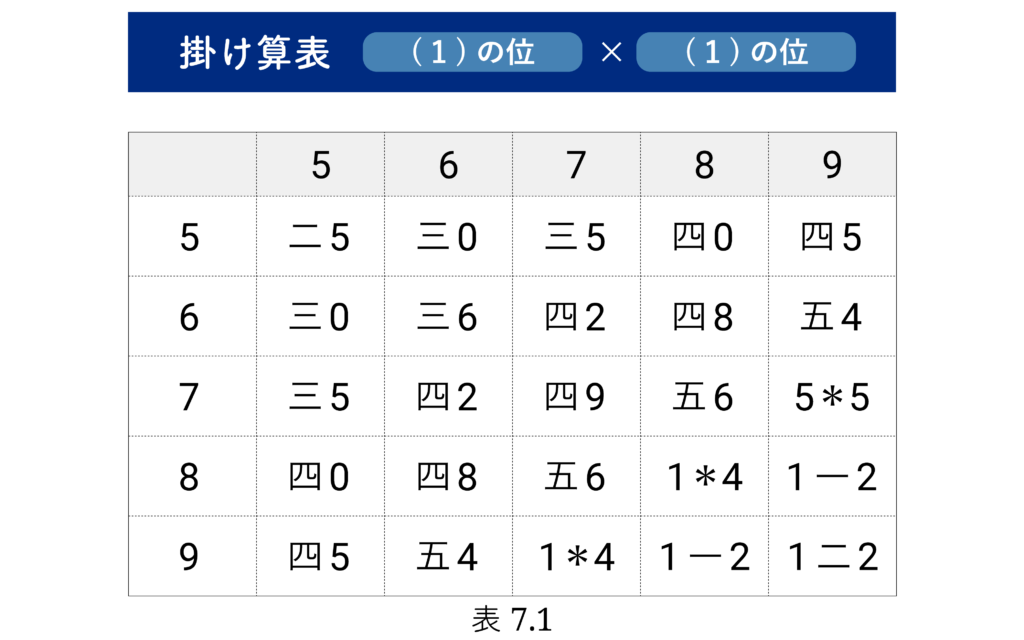
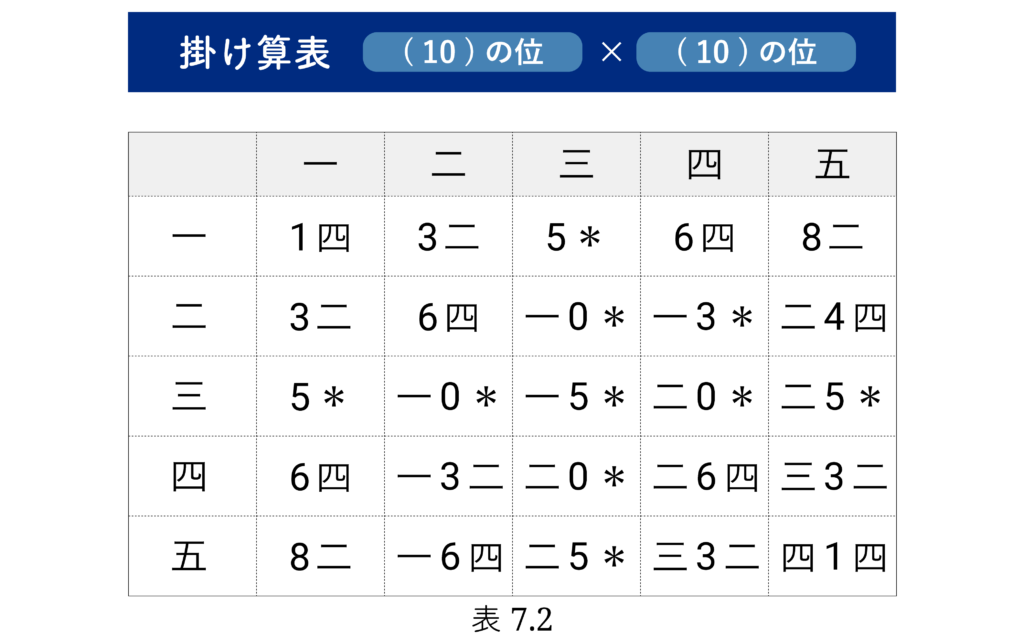
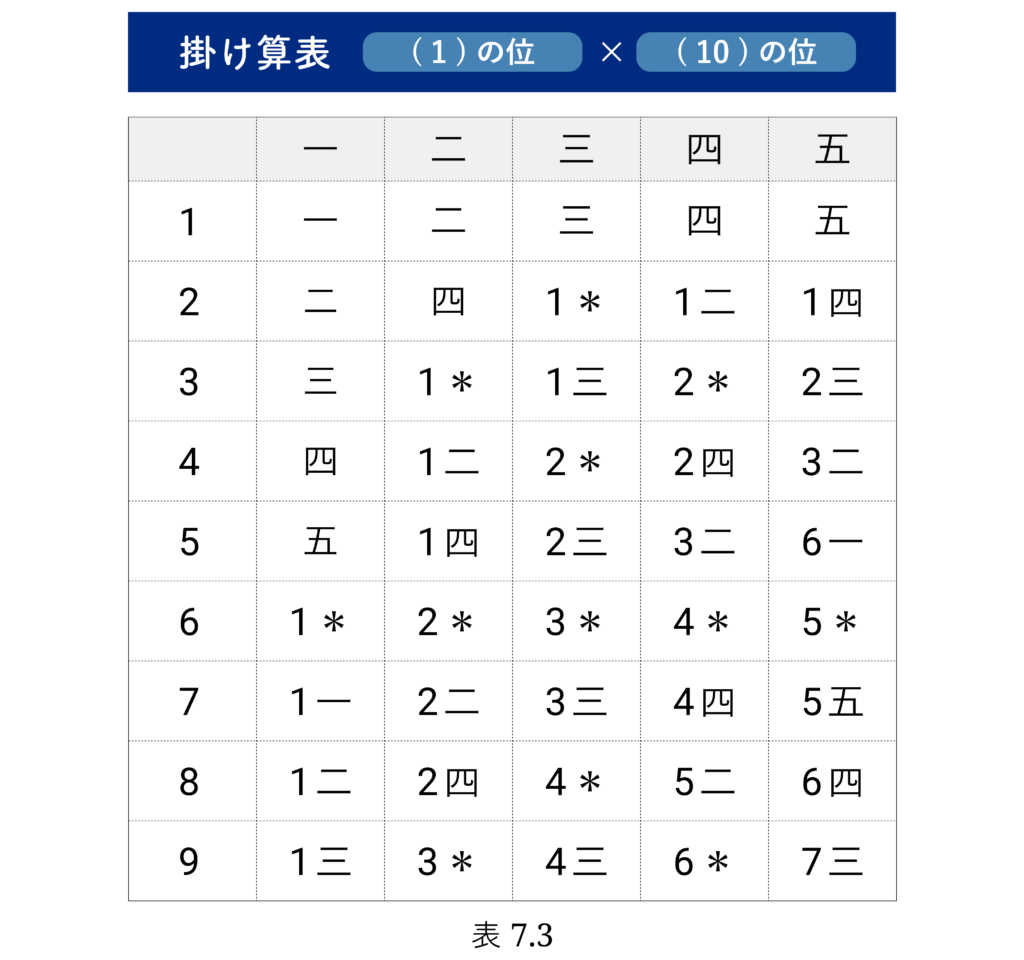
60進の「1桁×1桁」の掛け算ができれば、10進数と同様の方法で何桁の掛け算でもできますから、まず1桁同士の掛け算を考えます。
[(1)の位]×[(1)の位] の掛け算表で桁上がりがないものは皆さんよくご存じだと思うので省略してあります。7×8 の値は10進数では 56 ですが、60進数では 五6 と書きます。7×9 の値は10進数では 63 ですが、60進数では 10 の位は 6 で桁上がりするので 1*3 と書きます。正確には *1*3 と書くべきなのですが、最上位の * (ゼロ) は省略することにします。次の式では60進表記と10進表記が混在していますが、漢数字を含むものは60進表記、含まないものは10進表記です。等号で結ばれているのは数としては同じ値であることを意味します。

次に [(1)の位]×[(10)の位] の 7×四 を見てみましょう。
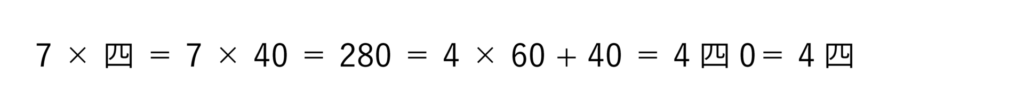
[(1)の位]×[(10)の位] の値の最後は必ず 0 となりますが、この 0 は省略することにします。
次に [(10)の位]×[(10)の位] の 二×四 と 四×四 を を見てみましょう。
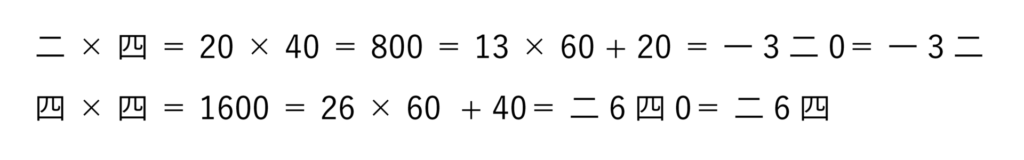
これも最後の 0 は省略することにします。
60進1桁同士の掛け算 34×38 と 56×38 を表7.1 – 7.3の掛け算表を使って計算してみましょう。
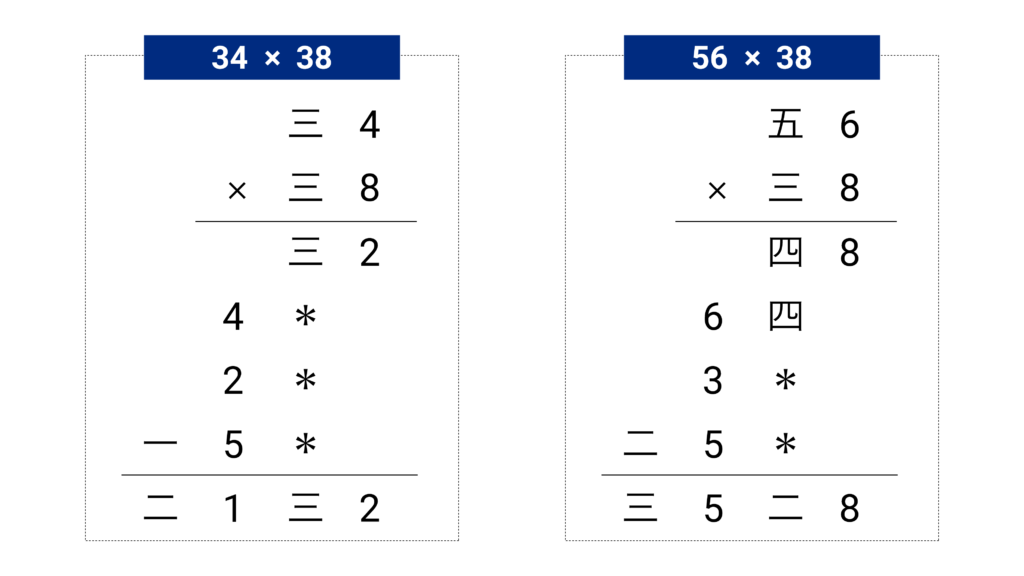
この計算を利用して 2696×38 を計算してみましょう。2696 = 34×60+56 = 三4五6 なので上の計算が利用できます。実はどのような順番で計算したのかわからないので、私たちが10進で計算しているように 60進で計算してみます。

掛け算表を使った計算はいかがでしたか?新しい記法を使っているので少し難しく感じた方もいるかもしれません。
これまで見てきたように、バビロニア人は60進数の足し算や掛け算を行なっていましたが、驚くべきことに、バビロニア人はこの時代に「小数の概念」も持っていたのです。〔 8.バビロニアの小数 〕もぜひご一読ください。

