6.ローマ数字と2･5進法

現在私たちが知っている60進数は時間と角度ぐらいで、皆さんは60進数の計算はあまり経験がないと思います。〔4.バビロニアの60進法〕では足し算を見ましたが、60進数の掛け算はどのように計算していたのでしょうか。60×60の掛け算表を使っていたのでしょうか。60×60は表が大きすぎます。計算の仕方を見ると、バビロニアの数は純然たる60進数と見るより、少し違った見方をした方がよいかもしれません。60進数の計算方法を学び、60進数という記数法をどのように解釈すればよいか考えてみましょう。

数の計算盤：古代ギリシア・中世ヨーロッパ・日本のソロバン

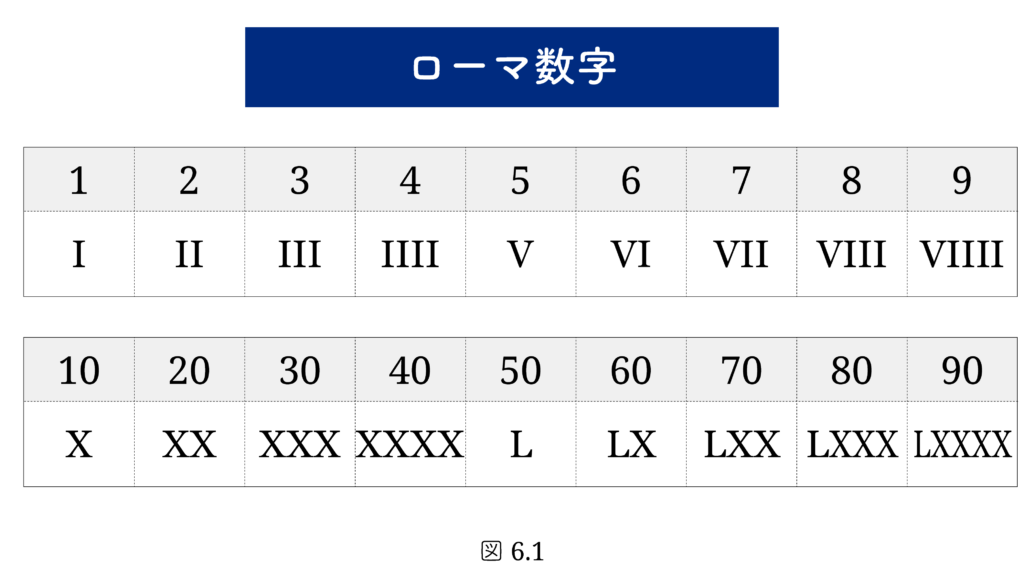
本題の60進数の計算方法に入る前に、まずは中世ヨーロッパを見てみましょう。ローマ数字では、1 ～ 9 と10 ～ 90 は次のように書きます( 図6.1 )。

〔 1.たばね法 〕でも述べましたが、古代の人々は計算盤を使って計算を行なっていました。計算盤にはいろいろなタイプのものがあります。図6.2(a) はギリシアの計算盤(アバクス)、図6.2(b) は中世ヨーロッパで使われた計算盤(アバクス)です。図6.2(a) の計算盤では、右端の欄から順に、一, 五, 十, 五十, 百, 五百 の位を表します。

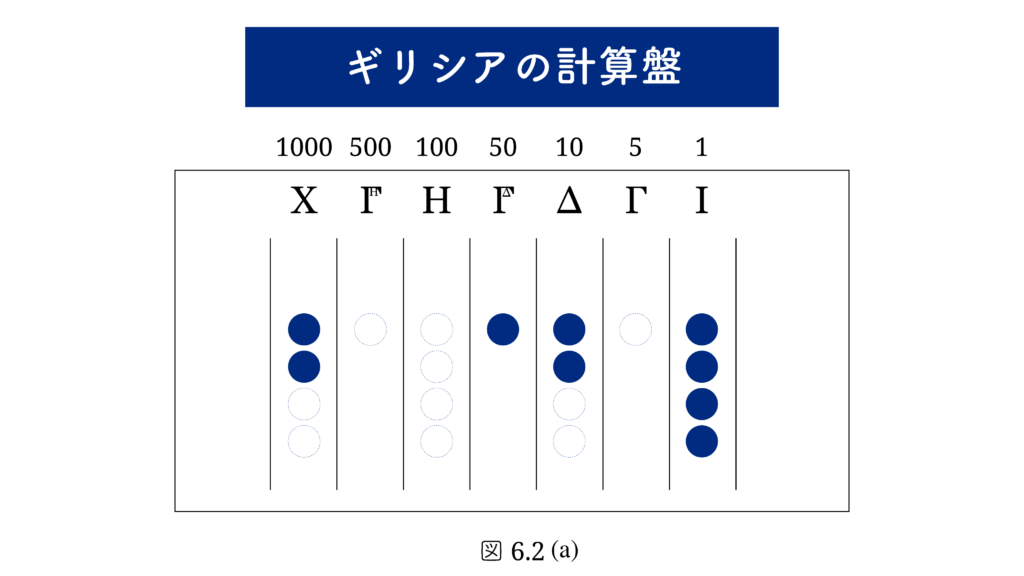
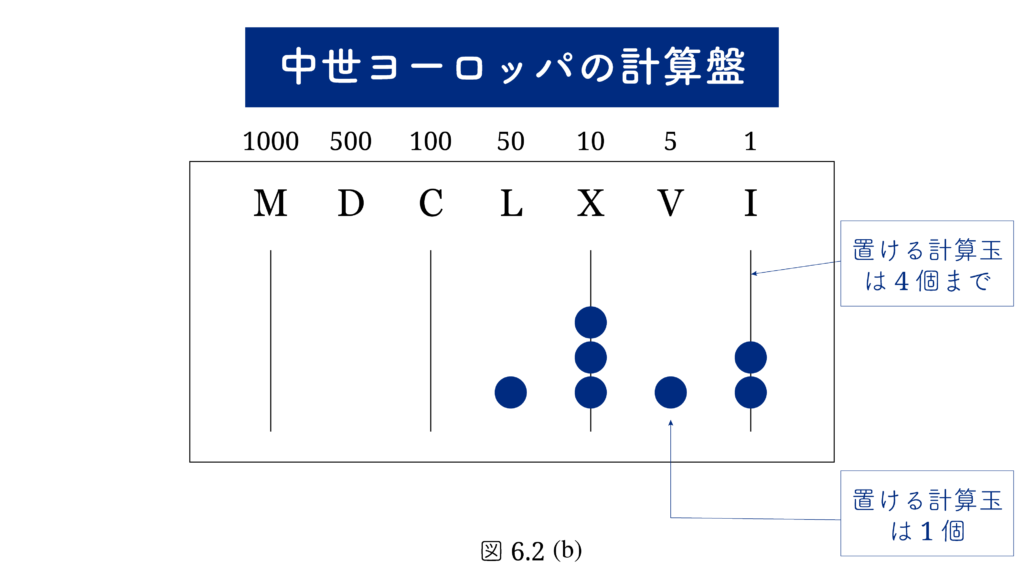
図6.2 (b) の計算盤では、計算玉を線上か、あるいは線と線の間に置きます。一番右の線は一の位、次の線が十の位、次が百、次が千の位です。線と線の間には計算玉を一個置くことができます。一番右の線と二番目の線の間は五、二番目と三番目の間は五十、三番目と四番目の間は五百を意味します。一、十、百、… の位は 5個計算玉がたまると上の位に繰り上がる5束法、五、五十、五百、… の位は 2個計算玉がたまると上の位に繰り上がる2束法と見ることができます。したがってローマ数字は、2束法と5束法が規則的に交互に繰り返す 2・5進法と見ることができます。

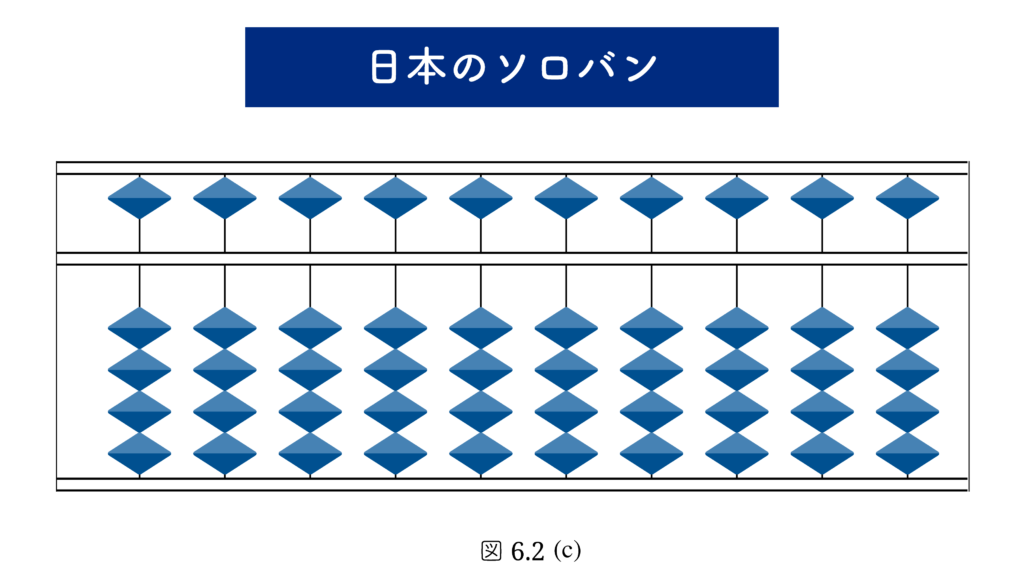
次に日本のソロバンを見てみましょう。図6.2 (c) は日本のソロバンです。日本のソロバンも五の珠(たま)と一の珠がありますが、これらは別々に用いられるのではなく一体として用いられています。

また、日本では奈良時代には九九が使われていたようです。このことは万葉集に言葉遊びとして九九が出てくることから分かります。柿本人麻呂、大伴家持、山部赤人などといった有名な歌人たちは、「二二を“し”、十六を“しし”、八十一を“くく”」と読ませています。このように奈良時代では、少なくとも万葉集を詠む人々にとっては、九九は常識だったようです。九九が存在したということは、「複数桁×複数桁」の掛け算のアルゴリズムが知られていたことを意味します。「一桁×一桁」や「複数桁×一桁」の掛け算では九九は必要ないからです。

ヨーロッパの掛け算方法：エジプト式の2倍法

ヨーロッパでいつ頃から九九が用いられるようになったかはっきり分かりませんが、おそらく14世紀までは使われなかったと思われます。16世紀になるとアラビア数字が普及し、計算盤に代わって筆算による計算が行われるようになると九九が使われるようになります。当時九九のことを“ピタゴラス表”と呼んでいましたが、もちろんピタゴラスの時代は九九などありません。では、ヨーロッパの人たちは掛け算をどのように計算していたのでしょうか。ヨーロッパでは掛け算はエジプト式の2倍法でした。2倍法では次が許されるように拡張されました。

(2倍), 3倍, (4倍), 5倍, 10倍

4倍は2倍を2回繰り返せばできます。古代エジプトでは3倍は表を使うかあるいは暗記していたようですが、a の3倍は 3a ＝ 2a＋a でも計算できます。10倍は10進法なら簡単です。5倍は、10倍を半分に割ります。これらは九九を知らなくてもできます。

古代では計算玉か計算盤を使いますが、ここでは代わりに式を使います。まず「複数桁×一桁」の計算をしてみましょう。a×7 は a×5＋a×2 と計算します。たとえば

83×7 ＝ (50＋30＋3)×(5＋2) ＝ 50×5＋30×5＋3×5 ＋ 50×2＋30×2＋3×2
＝500/2 ＋ 300/2 ＋ 30/2 ＋ 100 ＋ 60 ＋ 6
＝ 500＋50＋30＋1 (＝ 581)

となります。計算は長いですが単純作業です。「複数桁×複数桁」の計算は、たとえば

83×72 ＝ 83×70 ＋ 83×2             上の計算を使って
＝ (500＋50＋30＋1)×10 ＋ (50＋30＋3)×2
＝ (5000＋500＋300＋10) ＋ (100＋50＋10＋5＋1)
＝ 5000＋500＋400＋50＋20＋5＋1

となります。

このように、エジプト式の2倍法の拡張を使えば、ローマ数字でも私たちが行っている掛け算と大差ない手間で掛け算の計算をすることができます。

しかし、ローマ数字の最大の欠点は 位取り方式ではない ことです。ですから中世のヨーロッパの人々がエジプト式の「2倍法」あるいは「2分法」を使っていたとしても、現在の私たちの掛け算のように組織立ったアルゴリズムを持っていたかどうかは分かりません。

ローマ数字の掛け算を位取り方式で考える

2・5 進法の足し算

ここで、ローマ数字を位取り方式の記数法に変更して、上で述べた掛け算アルゴリズムを形式的な形で表してみましょう。これは中世ヨーロッパの人びとがこの方式で掛け算をしていたということではなく、次に述べるバビロニアの60進数の掛け算の理解のためです。以下に述べる記数法を、ここでは 2･5進法と呼ぶことにします。

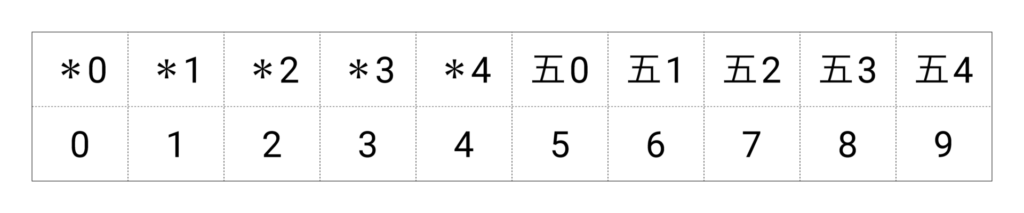
2･5進法 の記数法では、ローマ数字の代わりに次の数字を用います。

一、 十、  百、  千、 … の位は  0, 1, 2, 3, 4
五、五十、五百、五千、… の位は　＊, 五

ここで 0 と ＊ はその位に計算玉がないことを表します。たとえば 845 は 2･5進法 では

五3＊4五0                   DCCCXXXXV

となります。右は対応するローマ数字です。

2文字ずつ区切って下の数字で置き換えると通常の10進数になります。

練習のため足し算 74 ＋ 87 をやってみましょう。上の表より、7 は 五2、4は ＊4 と表されることに注意してください。

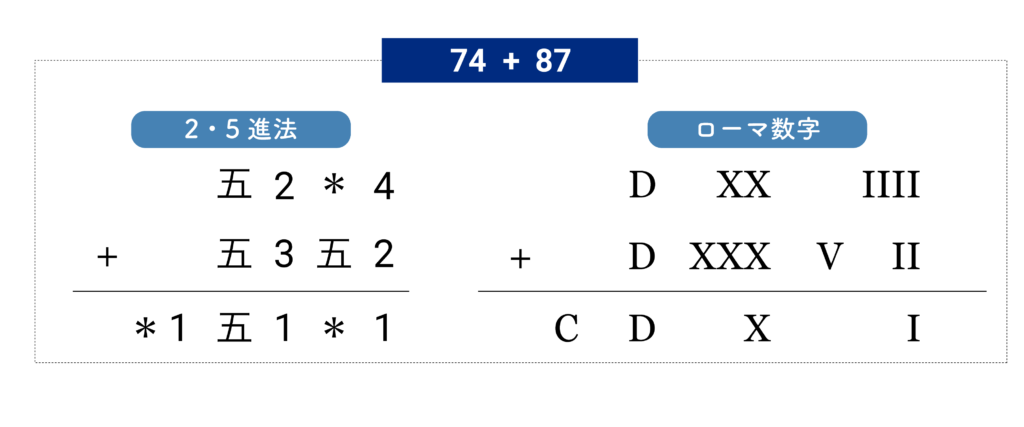
1桁目は 4＋2 ＝ 五1 ですから、五 が桁上がりします。2桁目は 五＋五 ＝ 1＊ となり、3桁目に 1 が桁上がりします。同様に計算をつづけ、＊1五1＊1 ＝ 161 となります。

2・5進法の掛け算

次に掛け算を考えましょう。4以下の a と b に対しては、次を知っていれば十分ですが、これぐらい暗記するのはたやすいと思います。

2×3＝ 五1, 2×4＝ 五3, 3×3＝ 五4, 3×4＝ 1＊2, 4×4＝ 1五1

3×4＝ 1＊2 に注意してください。次は五の位の九九です。

五×2 ＝ 1＊,  五×3 ＝ 1五,  五×4 ＝ 2＊,  五×五 ＝ 2五

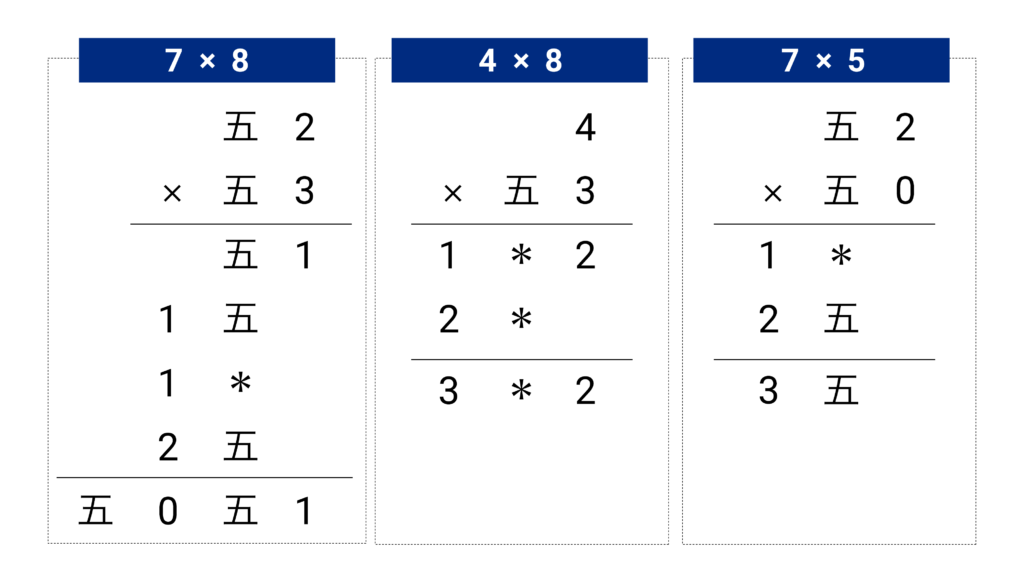
実際に計算してみましょう。10進で1桁の計算さえできれば何桁になっても、私たちが知っている組みたて算を使えば計算できます。7×8 と 4×8 と 7×5 を計算してみましょう。

次に 74×8 を計算してみましょう。これを 2·5 進法で表すと 五2＊4 × 五3 となります。計算する順序はいろいろありますが、たとえば次のように計算します。途中の桁上がりの計算は省略しました。

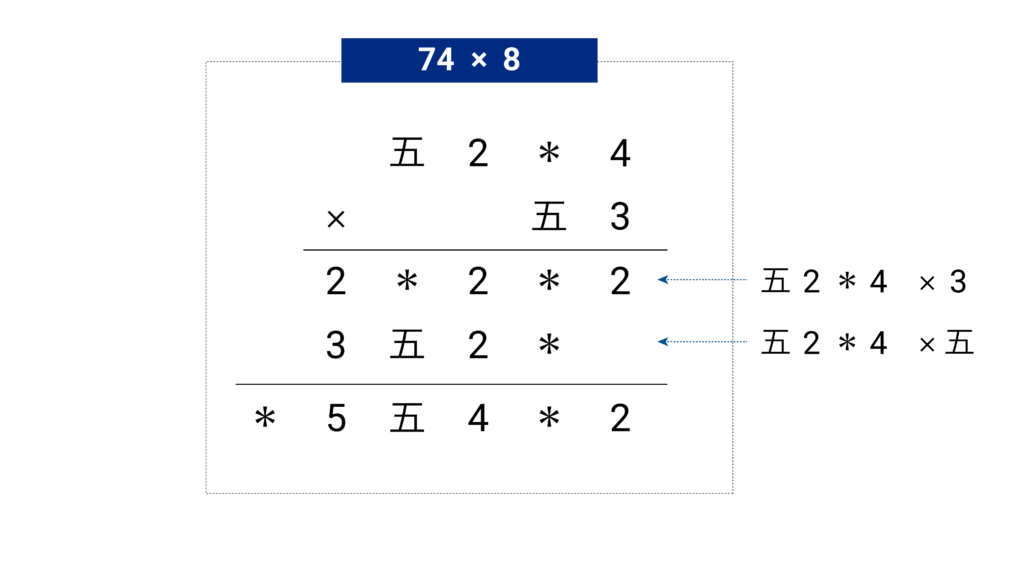
慣れないうちはとまどうかも知れませんが、慣れれば10進数の計算と同じような感覚で計算できるようになると思います。