最も美しい比率ー黄金比ー
それは「最も美しい比率」とも呼ばれ、古代ギリシアの数学から現代のデザイン、そして自然界にまで広く登場する神秘的な数です。
本記事では、
フィボナッチ数列との関係、五芒星やピラミッドに現れる構造、さらには自然界に見られる黄金比のパターンまで、
黄金比の魅力をわかりやすく紹介していきます。
身の回りに潜む「美しさの法則」を、数学の視点から一緒に探ってみましょう。
黄金比とは
「黄金比（golden ratio）」とは、人が最も美しいと感じる比率のひとつです。美術作品や建築、商業デザインにも多く取り入れられており、皆さんも一度は「黄金比」という言葉を耳にしたことがあるのではないでしょうか。
では、この「黄金比」とは具体的にどのような比率なのでしょうか？
黄金比の定義と計算方法
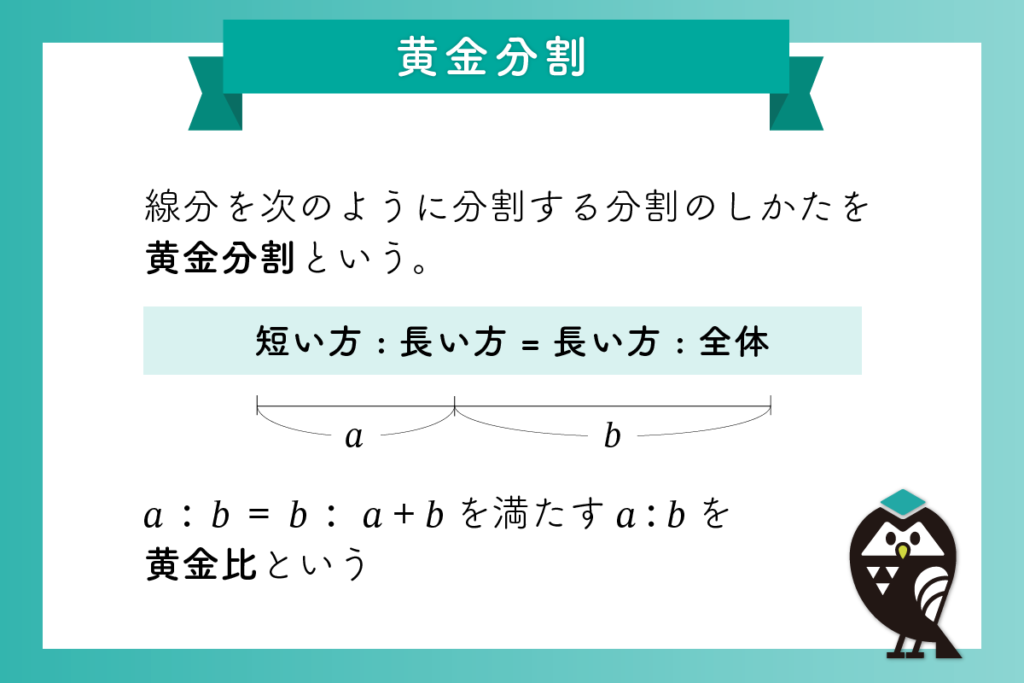
図1のように、線分ABを点Cで2つに分割してみましょう。ACを短い部分 a、CBを長い部分 bとします。このとき、次の関係を満たすように分割された比率を「黄金分割」と呼びます：
短い方 : 長い方 = 長い方 : 全体
これを式で表すと、次のようになります。
\(a:b=b:a+b\)(1)
この関係を満たす比率 b/a または a/bを、 黄金比 と呼び、その比率の値（およそ 1.618…）は、 黄金率 ともいわれます。
この比率は、ギリシア文字 φで表されることが多く、自然界の構造や古典建築、五芒星などにも現れることで知られています。
黄金比の計算
前述の関係式 (1) に外積＝内積の関係を適用すると、次のような式が導かれます：
\(b^2=a\times(a+b)\)(2)
この式（2）の両辺を a^2 で割り、x = b / a とおくと、次の二次方程式が得られます：
\(x^2=1+x\)(3)
この方程式（3）を解くと、正の解は以下のようになります：
\(\varphi=\frac{1+\sqrt{5}}{2}=1.6180339887\ldots\)(4)
となります。この φ が黄金率で、1 : φ が黄金比です。
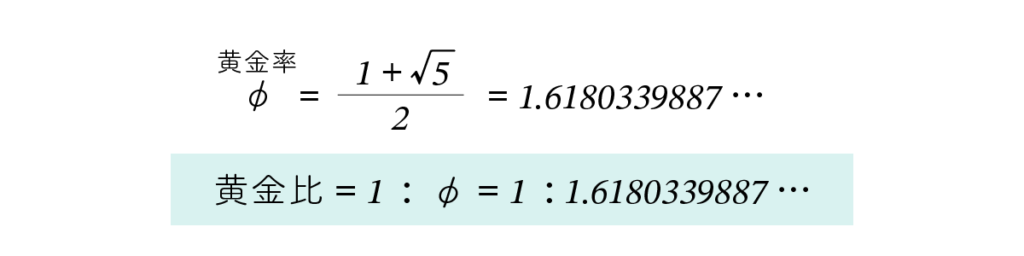
黄金比とフィボナッチ数列の関係
黄金比 φ（ファイ）は、自然界にも現れる美しい比率として知られています。実はこの黄金比、フィボナッチ数列と深い関係があります。
フィボナッチ数列とは？
フィボナッチ数列は、次のような数の並びです：
\(1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ 233,\ \ldots\)
この数列の隣り合う数の比（後の数 ÷ 前の数）を順に計算してみましょう：
\(\frac{1}{1}=1\)
\(\frac{2}{1}=2\)
\(\frac{3}{2}=1.5\)
\(\frac{5}{3}\approx 1.666\ldots\)
\(\frac{8}{5}=1.6\)
\(\frac{13}{8}\approx 1.625\)
\(\frac{21}{13}\approx 1.615\ldots\)
\(\frac{34}{21}\approx 1.619\ldots\)
このように、比の値は次第に φ（1.6180339887…）に近づいていきます。
フィボナッチ数列の隣接項の比は、黄金比に収束することがわかります。この性質は、植物の葉の配置や貝殻の渦、銀河の形状など、自然界の多くの現象とも関連があると言われています。
ギリシア数学における「比」の概念とは？
古代ギリシア数学の特徴のひとつは、「比」という考え方に重きを置いていた点です。なかでも、今回のテーマである黄金比（古代では「外中比」）は、特に注目されてきました。
ギリシア幾何学では数値を使わない？
ギリシアの数学、特に「幾何学」は、定規とコンパスのみを用いて構築されていました。ここでは数値を用いず、図形的な構成や関係に基づいて理論を展開します。
これは「数値を使ってはいけない」という禁止ではなく、数学を構築する前提として“数値”が存在していなかったことによります。ギリシア幾何学では、まず定義や公理（使ってよい概念）を明確にしたうえで、論理を積み重ねていくスタイルがとられていたのです。この方式はギリシア以降数学の標準として踏襲されてきます。
「比」は数値ではなく、2つの量の関係
古代ギリシア人にとっての比 a : bは、現代のように「b ÷ a」という数値そのものを意味するのではなく、2つの量aとbのあいだの“関係”を表すものでした。
また、無理数 φ（ファイ）＝1.618… のような概念も、当時は「数」としては認識されていません。無理数が数学の中で「数値」として扱われるようになるのは、もっと後の近世以降のことです。
では黄金比はどう扱われていたのか？
数値としての黄金比（1.618…）が使えなかった古代において、黄金比は図形的な比として捉えられていました。たとえば、五芒星（ペンタグラム）に現れる辺の長さの比は、黄金比を自然に含んでいます。
ギリシア幾何学では、このような図形の中に現れる比の関係を通じて、黄金比の美しさや構造を理解していたのです。
次にギリシア幾何学によく出てくる五芒星を見てみましょう。
五芒星と黄金比
図形の中に隠された、美しき比率
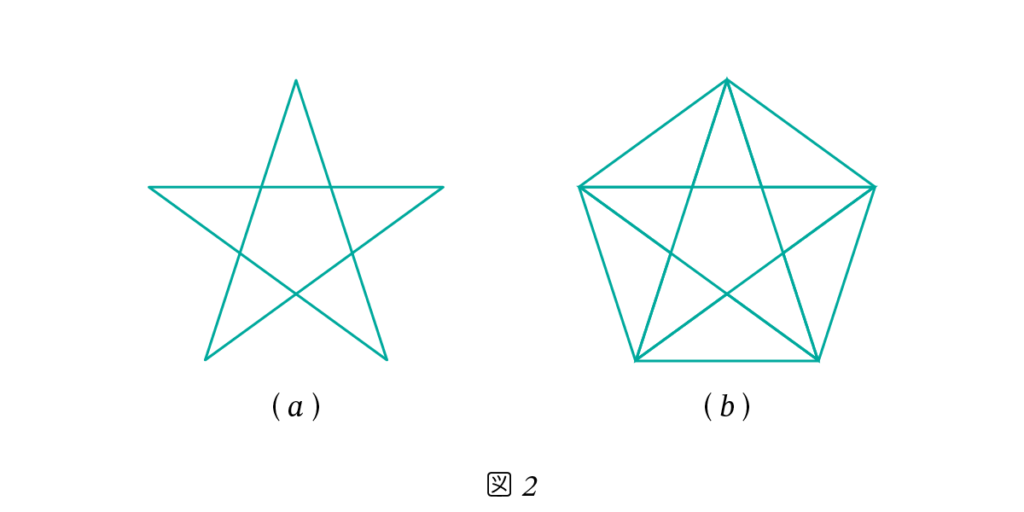
図2-(a) に示されるような星形の図形を 五芒星（ペンタグラム） と呼びます。この五芒星は、古代ギリシアのピタゴラス学派にとって特別な意味を持ち、教団のシンボルとして大切にされていました。
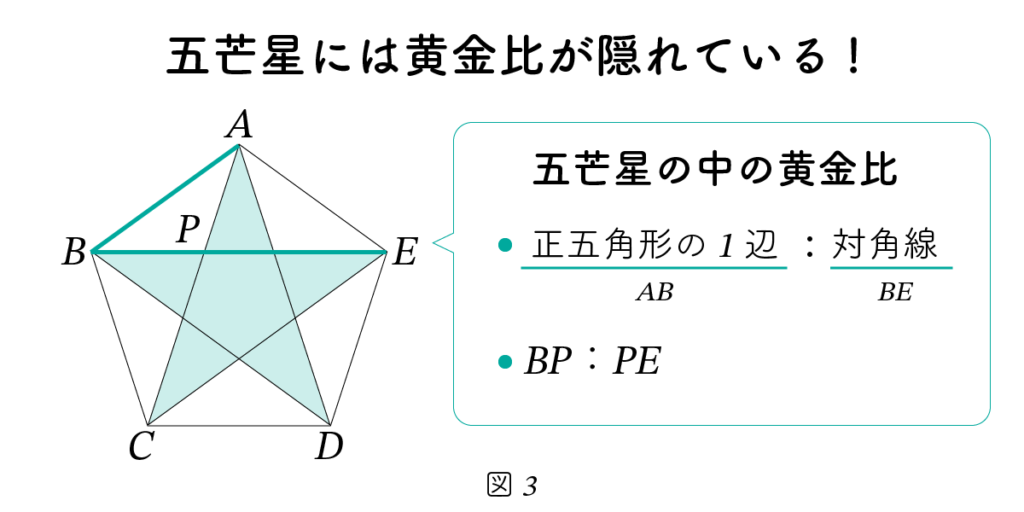
五芒星の中には、黄金比が繰り返し現れます。たとえば、五芒星の頂点同士を線で結ぶと、図2-(b) のように 正五角形が浮かび上がります。この正五角形の中にも、さまざまな場所に黄金比が隠されています。
なかでも代表的なものが、図3の AB : BE の比、すなわち「正五角形の1辺 : 対角線」に表れる黄金比です。
自然界にも現れる黄金比
黄金比は図形の中だけでなく、自然界にも数多く登場します。たとえば、木の葉の配置、貝殻の渦巻き、花びらの並びなどにも、この比率が見られるのです。
こうした自然の美しさに黄金比が関わっていることは、ピタゴラスが唱えた「自然は数の比によって支配されている」という思想を裏付けるものだと考えられてきました。
黄金長方形 〜繰り返し現れる美しい構造〜
図形の中には、自分自身と相似な形を内側に持つという特徴をもつものがあります。このような構造は、再帰構造（recursive structure）と呼ばれます。その代表例が、「黄金長方形」です。
黄金長方形とは？
縦横の比が黄金比（a : b）である長方形を 黄金長方形 と呼びます。この黄金長方形から、一辺の長さが a の正方形を切り取ると、残りの部分もまた黄金長方形になります。
この操作は何度でも繰り返すことができ、正方形を次々と切り取ることで、無限に続く再帰的な構造を作り出すことが可能です。図4は、このようにして形成された黄金長方形の例です。
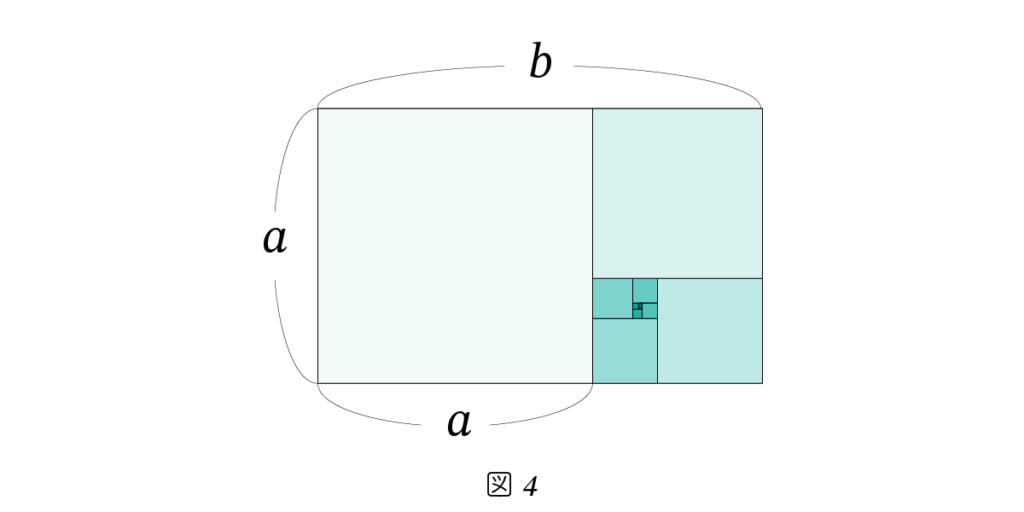
自然界に見られる黄金長方形の構造
この再帰的な構造は、巻貝の螺旋など、自然界の中にも実際に見られるパターンです。自然が生み出す美しさの中に、黄金比のような数学的構造が存在していることは、私たちにとっても驚きと魅力を与えてくれます。
ピラミッドにも『 黄金比 』が隠されている？
エジプトの大ピラミッドは、世界七不思議のひとつに数えられ、古代から多くの人々の関心を集めてきました。そのなかでもよく語られる謎のひとつが、「ピラミッドには黄金比が隠されている」という話です。
底面積と側面積の比が黄金比に？
この説によれば、大ピラミッドの底面積（S₁）と側面積（S₂）の比が、黄金比 φ（ファイ）＝1.6180339887… に一致するというのです。
式で表すと、
\(\frac{S_1}{S_2}=\varphi=1.6180339887\ldots\)
が成立するというのです。実際に計算してみると、確かにこの比率は黄金比に非常に近い数値になることがわかります。では、これは偶然なのでしょうか？それとも、古代エジプト人が意図してこの比を設計に取り入れていたのでしょうか？
Web連載【ピラミッドに隠された謎】では、この「黄金比の謎」を古代エジプトの歴史や神話、そして古代エジプトの数学能力など、様々な角度から解き明かしていきます。興味のある方はこちらもぜひ読んでみてください▼
まとめ
黄金比は、単なる数値ではなく、数学・自然・美の交差点とも言える特別な比率です。
- 黄金比は「短辺 : 長辺 = 長辺 : 全体」という比率から導かれ、数式では φ = (1 + √5) ÷ 2 ≒ 1.618…（約1.618）で表されます。
- フィボナッチ数列の隣接項の比は、この黄金比に収束していきます。
- 五芒星や黄金長方形のような図形、貝殻や植物の配置、さらにはエジプトのピラミッドにも黄金比は現れるとされています。
古代の哲学者たちが見つめ、現代の芸術家や科学者までも魅了し続けるこの比率。
「なぜ美しいと感じるのか」という問いに、黄金比は一つのヒントを与えてくれるかもしれません。