2進法の原理とは？ライプニッツが着目した数のしくみ

微積分学の創始者、ライプニッツ

現在のコンピュータの内部では、数は2進数で表現され、2進数をもとに設計されています。この2進数の重要性に最初に注目した人物のひとりが、17世紀の大数学者 ライプニッツ です。彼はニュートンと並んで 微積分学の創始者 とされ、数学史において非常に重要な存在です。

ライプニッツの父親は大学教授であり、彼は幼いころからギリシア語やラテン語の古典を読み、古代の哲学や幾何学を学びました。また、神学にも深い関心を寄せ、21歳のときには錬金術協会に参加して金を作ろうと試みていたことも記録されています。

ライプニッツが2進数に注目したのは、必ずしも数学的な動機からではなく、むしろ神秘主義に基づくものでした。ある伯爵に宛てた手紙の中で、彼は「2進数は10進数と違って、宇宙の完全性を表し、10進数よりもはるかに多くの意味を含んでいる」と述べています。1は「神」、0は「無」を象徴し、2進数の構造そのものが「無からの宇宙の創造」を意味するのだと考えました。

彼はこの思想を、当時中国にキリスト教を伝道していたイエズス会の宣教師たちにも伝えるよう勧めており、2進数を単なる数学的道具ではなく、哲学的・宗教的な意味を持つ概念として捉えていたことがうかがえます。

10進数と2進数：数の表し方の違い

私たちは子どもの頃から「数」に親しんできましたが、普段使っているのはほとんどが10進数、つまり10進法で表された数です。そのため、数といえば「10進数」が当たり前だと感じてしまい、2進数など他の表現方法にはなじみにくさを覚えるかもしれません。

ここで注意したいのは、「10進数」や「2進数」という言葉は、数そのものの“種類”を指しているのではなく、数の表し方（表現方法）を指しているということです。

たとえば、私たちが「みっつ」や「三」と言ったり、英語で “three” と言ったりしても、どれも同じ「3」という数を意味しています。つまり、“3”という数自体はひとつしかなく、違うのはその表現のしかたにすぎないのです。

ですから、本来なら「10進表現」「2進表現」と呼んだ方が誤解が少ないのですが、「10進数」「2進数」という言い方が広く定着しているため、ここでもその慣例に従うことにします。

当は、“10進表現”とか“2進表現”と呼んだ方がよいのですが、すでに言い習わされた表現なのでここでは慣例に従うことにします。

10進数とは？

私たちが日常的に使っている「10進数」は、大きな数を扱いやすくするための記法が工夫されています。たとえば、数「304005060」は「三億四百万五千六十」と書き表すことができます。ただ数字を並べるよりも、「億・万・千・百・十」といった単位（桁標識）を用いることで、数の構造がはっきりし、理解しやすくなります。

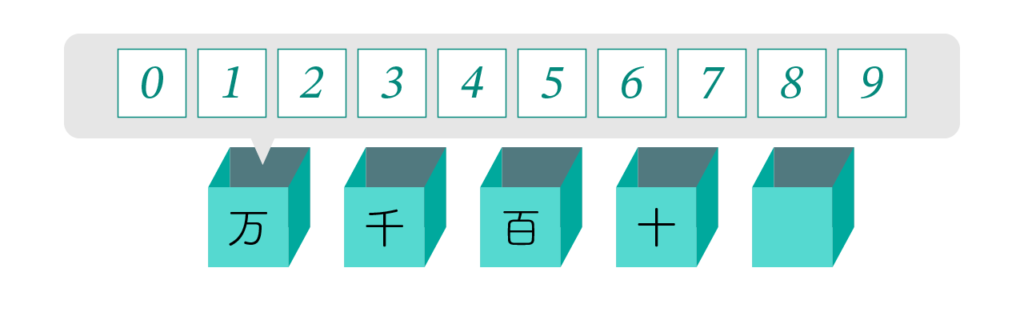
「億」「万」「千」などの単位は、各桁の重みを示す桁標識と呼ばれます。ソロバンに親しんでいる方なら、各桁の上に桁名が書かれたソロバンを思い浮かべてください。ソロバンに馴染みがない場合は、下の図のように桁標識のついた箱が横一列に並べられている様子を想像すると理解しやすいでしょう。

なお、最も右端の桁（最下位）には通常、桁標識はついていません。

各箱には 0 から 9 までの数字の一つが入ります。

たとえば 6, 5, 4, 3, 2 がそれぞれの箱に入った場合、これが表す数値は「 6万5千4百3十2 」となります。

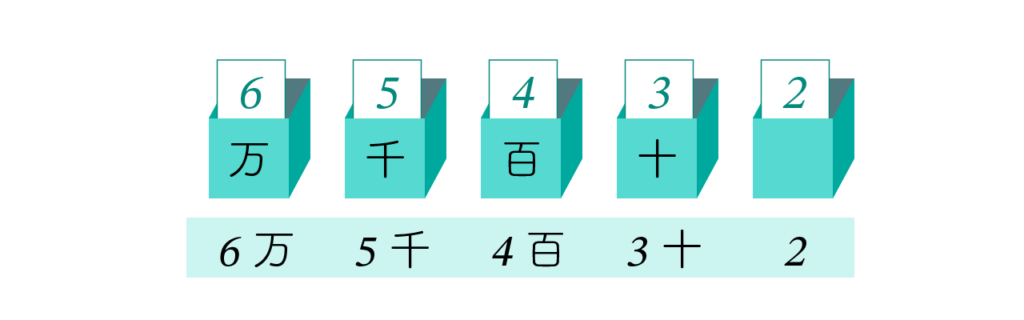
このように、10進数は「1から9までの数字を入れた箱が並んだもの」をイメージしてみてください。

2進数とは？

2進数では、数字を表すために「0」と「1」だけを使います。まず、下の図のように箱を並べて考えます。10進数では各桁に0〜9までの数字が入りますが、2進数では各箱に入るのは「0」か「1」だけです。

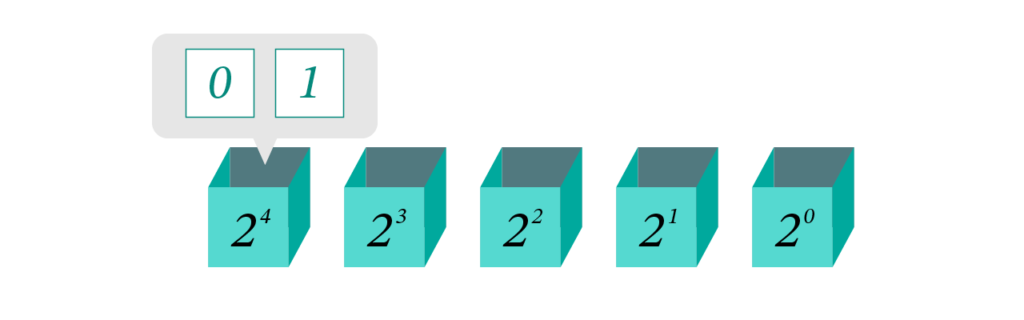
それぞれの箱に 1、0、1、0、1を入れてみましょう。この2進数が表す数は以下のようになります。

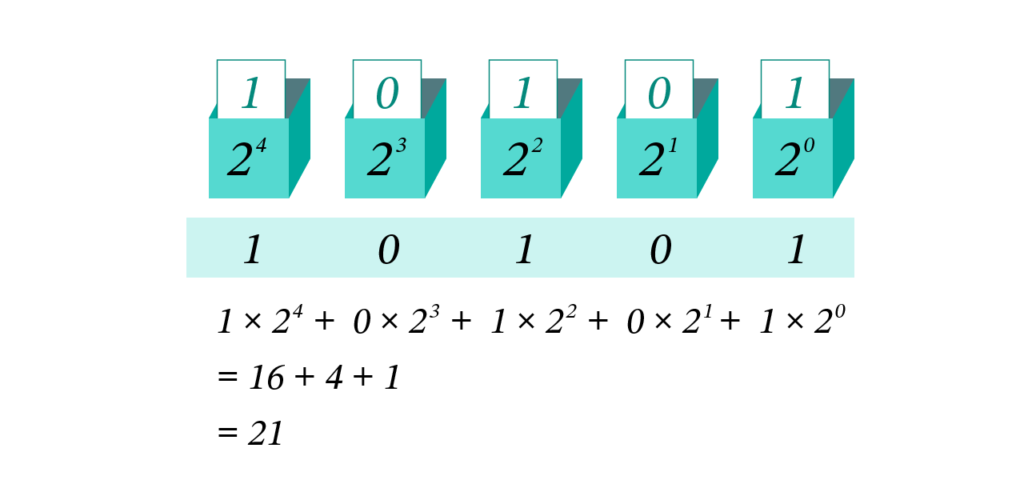
ヤードポンド法と2進的な単位の考え方

厳密に言えば「2進数」とは異なりますが、古代から 2倍ずつ増えていく単位系 というのはさまざまに存在していました。その一例が、ヤードポンド法における液体の容量の単位です。

たとえば、次のような順に単位が並んでいます：

ジル → チョピン → パイント → クォート → ポトル → ガロン → ペック

最小単位の「ジル」を起点として、

• 2ジル ＝ 1チョピン
• 2チョピン ＝ 1パイント
• 2パイント ＝ 1クォート

… というように、それぞれが2倍ずつの関係になっています。このような2進的な構造の単位系では、数字ではなく単位の組み合わせで量を表すこともあります。たとえば「9ジル」は、「1パイントと1ジル」と表現するような具合です。

現在でも、イギリスやアメリカではこのようなヤードポンド法（尺貫法）が日常的に使われており、ワインなどの液体の計量にこの単位体系が使われる場面もあります。

貨幣の例で考える2進数のしくみ

外国の単位系は私たちにはあまりなじみがないため、ここでは想像上の貨幣の仕組みを使って、2進数の考え方をイメージしてみましょう。

たとえば、次のような6枚の硬貨があるとします：

• 1円硬貨、2円硬貨、4円硬貨、8円硬貨、16円硬貨、32円硬貨

6種類の硬貨で61円まで支払える

1円、2円、4円、8円、16円、32円──この6種類の硬貨が1枚ずつあれば、0円から61円までのすべての金額を支払うことができます。

42円を支払う方法① ― 上位の硬貨から引いていく

たとえば、42円を支払う方法を見てみましょう。

1. まず32円硬貨を使うと、残りは 42 − 32 = 10円。
2. 次に、16円硬貨は大きすぎるので使いません。
3. 8円硬貨を使うと、残りは 10 − 8 = 2円。
4. 最後に2円硬貨を使って合計42円になります。

使った硬貨は、32円、8円、2円です。

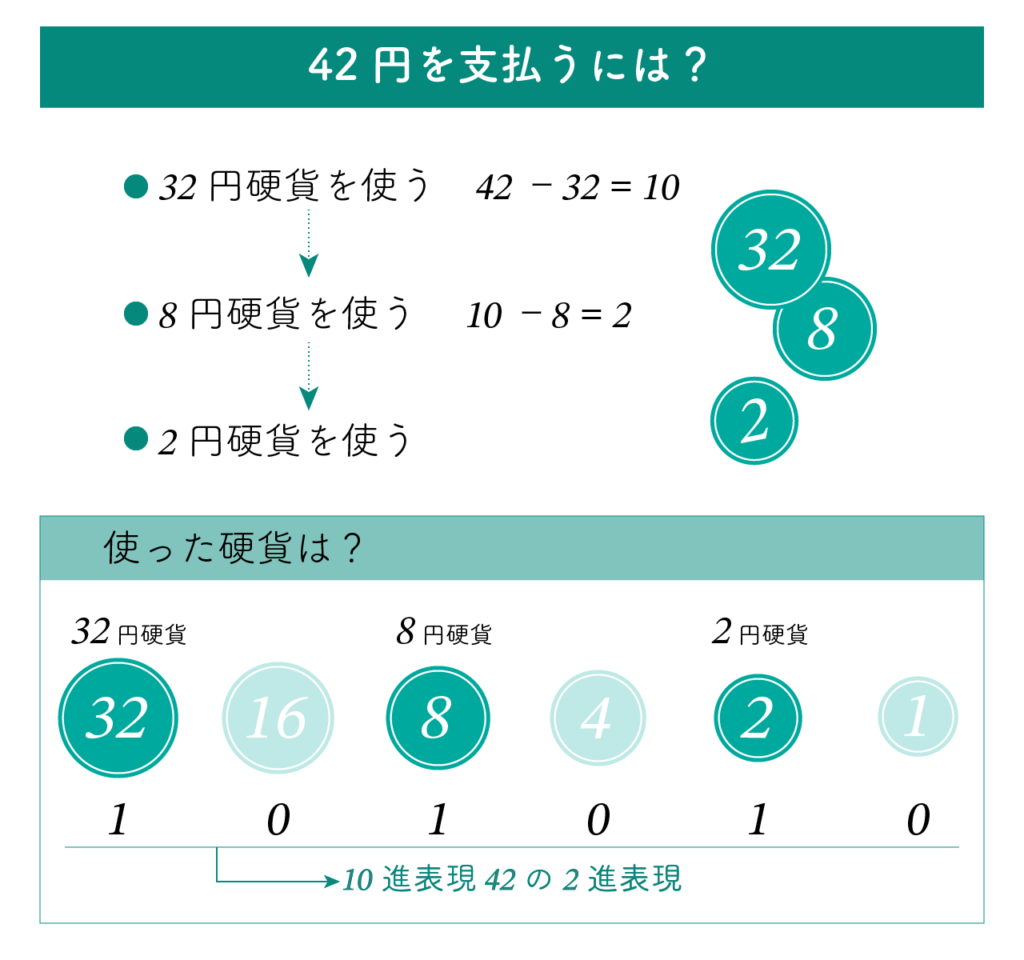
すると、使った硬貨は32円、8円、2円となります。使った硬貨を1で、使わなかった硬貨を0で表し、上の桁から並べると「101010」となります。この 101010 が10進表現 42 の2進表現です。

42円を支払う方法② ― 2で割っていく方法

今度は別の方法で、10進数の42を2進数に変換してみましょう。考え方は「2で割っていく」方式です。

1円硬貨が42枚あったとします。まずこれを2円硬貨に両替します。すると、2円硬貨が 21枚となります。2円硬貨を1枚使うことにします。20枚の2円硬貨を4円硬貨に両替すると、10枚の4円硬貨になります。これを8円硬貨に両替すると、5枚の8円硬貨になります。8円硬貨を1枚使います。残りの4枚の8円硬貨は2枚の16円硬貨に、2枚の16円硬貨は1枚の32円硬貨となります。

下から順に余りを並べると：101010

このようにしても、やはり42 = 101010 (2進数) となります。

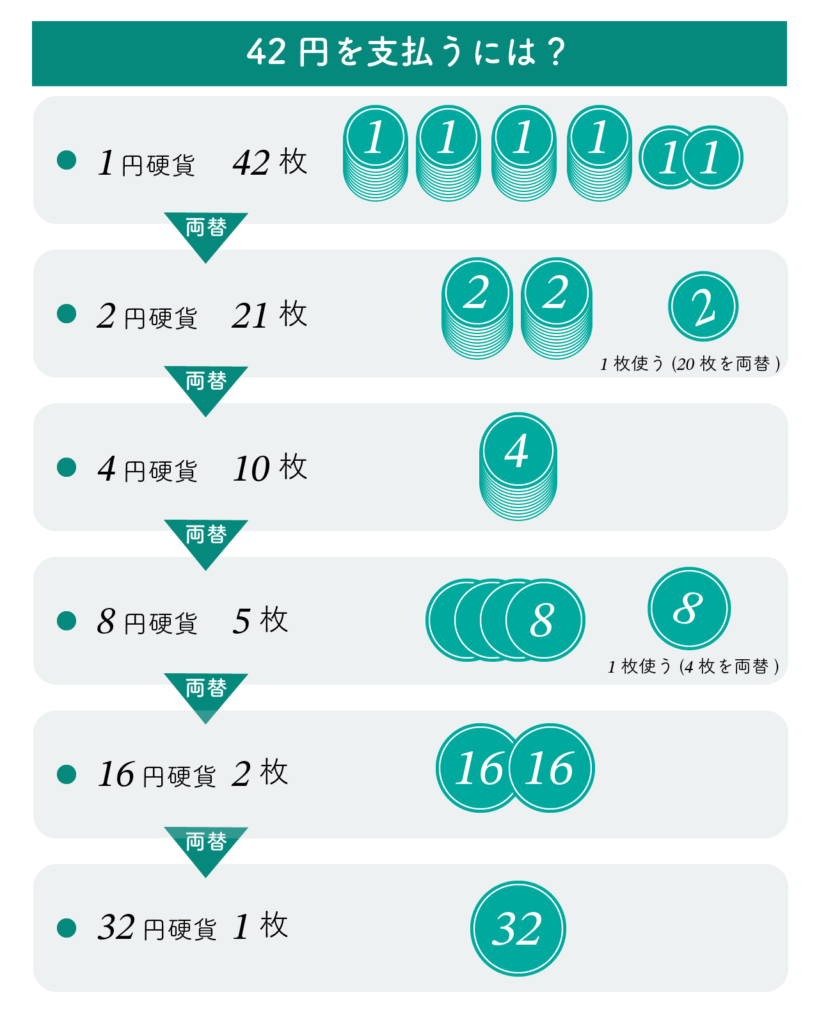
10進表現 42 の2進表現は？

次の図1は上で述べた「引いていく方法」の計算表、図2 は「2で割っていく方法」です。

図1 の中央の欄は 1, 2, 4, … を逆さまに並べた列です。左の欄から中央の欄を引き、引けたら右の欄に 1 を、引けなかったら 0 を記入します。図2では、左の欄を2で割っていきます。左の欄が奇数なら右の欄に1を、偶数なら 0 を記入します。2進数は、図1 では上から下へ、図2 では下から上に読みます。

このようにして、2通りの方法のどちらを使っても、10進数の42は、2進数では「101010」 と表されます。

これは「数を1か0かで表す」コンピュータの基本的な考え方と深くつながっています。

図でわかる！2進数のソロバン

2進数のしくみを視覚的に理解するには、図3 のような『2進数のソロバン』を使うとわかりやすくなります。
このソロバンでは、各桁に1個の珠（たま）だけがあり、それぞれが 「上がっている」か「下がっている」か で、1か0かを示します。

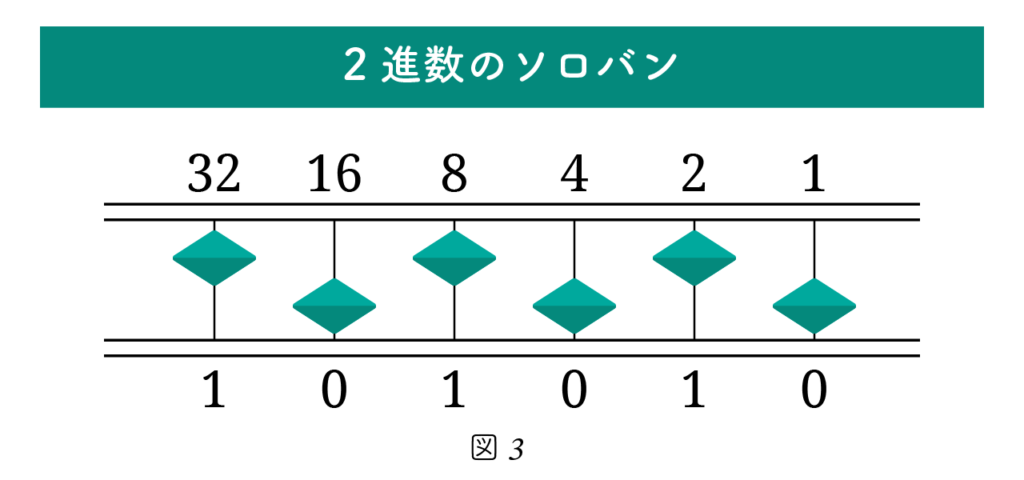
各桁の珠の状態は以下のようになっています。

桁の値	珠の状態	表す値
32	上がっている	1
16	下がっている	0
8	上がっている	1
4	下がっている	0
2	上がっている	1
1	下がっている	0

したがって、これが表す2進数は 「101010」10進数では 32 + 8 + 2 = 42 を意味します。

2進数は扱いづらい？

わずか100枚で、世界中の金額をカバーできる？

「2進数は桁数が多くなりすぎて、人間には扱いづらい」という声をよく耳にします。たしかに、小さな数を表すときは10進数に比べて桁数が多くなるため、直感的には見づらく感じるかもしれません。

しかし、大きな数になると、むしろその表現力の強さが際立ってきます。

たとえば、100枚の硬貨を使う場合を考えてみましょう。

2進数では、100桁の2進数で表せる数は

さらに、また〔完全数のお話〕で述べたように、2¹⁰ は 1,024 なので 10³（= 1,000）より大きい ということから、2¹⁰⁰は以下のように計算できます。

つまり、100枚の硬貨で10の30乗、すなわち

10³⁰ = 10¹⁸ × 10¹² = 10¹⁸兆

もの数を表すことができるのです。

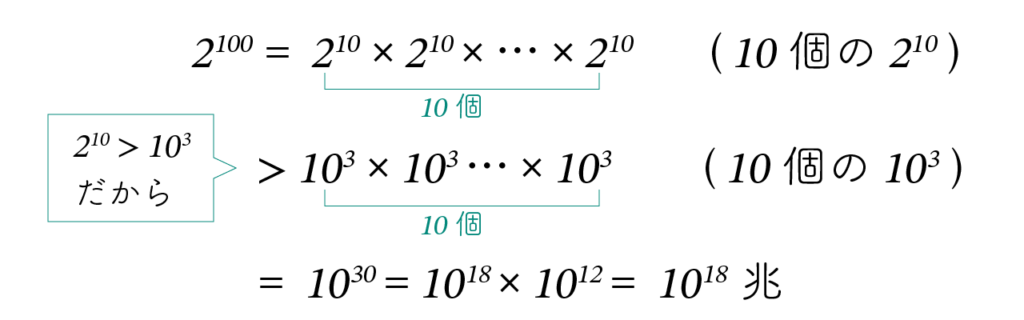
硬貨 100枚程度なら、少し大きめの財布なら十分に入ります。このように、2¹⁰⁰円 は世界中のお金をかき集めたよりもはるかに大きな金額となります。たった100枚の硬貨があれば、世界中で扱われているどんな金額でも表すことができるのです。

まとめ

2進数は、単にコンピュータの世界だけで使われている技術的な表現方法ではありません。17世紀にライプニッツが神秘的な魅力を感じたように、2進数には「万物を単純な要素から表現できる」という深い思想が隠されています。

また、現代においても、デジタル技術の根幹を支えるしくみとして不可欠な存在です。2進数の仕組みや可能性を知ることは、数に対する理解を深めるだけでなく、人類が数に込めてきた思想や文化の奥行きを知る手がかりにもなるのではないでしょうか。