黄金比 とは

黄金比とは──美と調和を生む不思議な比率

黄金比とは、人間が最も美しいと感じるとされる比率のことで、美術や建築、プロダクトデザインなど、さまざまな分野で活用されています。

この比率は、線分をある特別な方法で分けたときに現れます。その方法とは、線分を「短い部分：長い部分 ＝ 長い部分：全体」となるように分割すこと。このような分け方を黄金分割と呼び、そのときの比率が黄金比です。

黄金比の数式的な定義

たとえば、線分 AB を点 C で分割し、

• AC を短い部分（長さ a）
• CB を長い部分（長さ b）

とした場合、次の関係が成り立つときに黄金比が現れます：

a : b = b : a + b　　　( 1 )

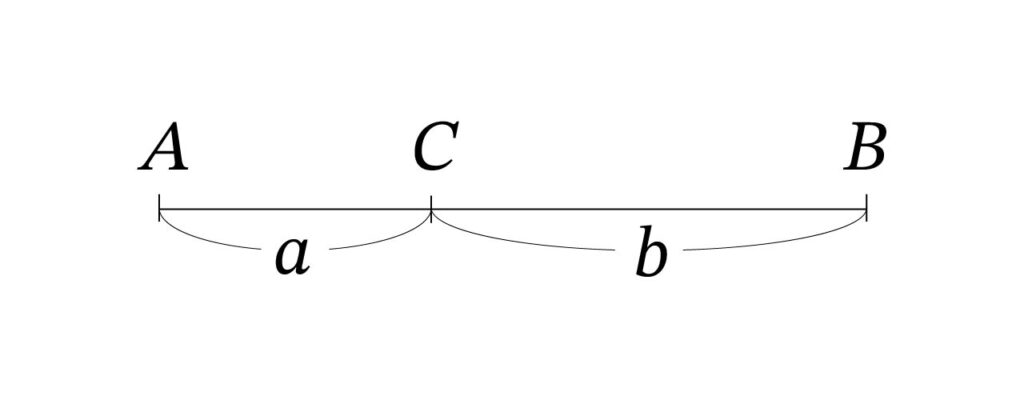
線分を二つに分割するとき、「短い方：長い方＝長い方：全体」となるように分割する分割のしかたを黄金分割と呼び、この時現れる比を黄金比といいます。下の図を見てください。

線分 AB を点 C で2 つに分割します。AC が CB より短いとし、ACの長さを a、CB の長さを b とします。

( 1 ) を満たすa : b を黄金比といい、b / a を黄金率と呼びます。（ b / a の逆数 a / b を黄金率と呼ぶこともあります。）黄金率はよくギリシア文字 φふぁいで表されます。

黄金比の計算──式から導く美の比率

「外積の項 = 内積の項」なので、 ( 1 ) は

b² = a × ( a + b )　　　( 2 )　

となります。( 2 ) の両辺を a²  で割り、x = b / a とおくと、次の二次方程式が得られます。

x²  = 1 + x　　　( 3 )

これは黄金比を表す二次方程式であり、その正の解が黄金比の値 φ（ファイ）です。

φ = ( 1 + √5 ) / 2 = 1.6180339887…　　　( 4 )

この値 φ が黄金率であり、比として表すと

1 : φ = 1 : 1.618…

が黄金比になります。

白銀比とは──日本文化に根ざしたもうひとつの美の比率

白銀比（はくぎんひ）は、1 : √2（約1 : 1.414）という比率のことで、黄金比と並んで「美しい」とされる比のひとつです。

この比率は、日本の伝統文化との関わりが深いことで知られています。たとえば、仏像の顔立ちや法隆寺の五重塔などの建築物において、この比率が用いられているとされています。

白銀比の実用性──紙の規格にも活用

白銀比は、実用面でも非常に優れた性質を持っています。特に、日本で使われているA4・B5などの紙の規格サイズは、この1 : √2 の比率に基づいて設計されています。

この比率を持つ長方形は、短辺を基準に半分に折っても、元の形と相似形になるという特性があります。そのため、折り畳んだり縮小・拡大しても比率が崩れず、無駄が出ないという点で非常に効率的です。

白銀比の魅力とは？

黄金比が「西洋的な調和と均整の美」とするなら、白銀比は日本的な静けさや端正さを象徴する美とも言われます。

私たちの身の回りにある紙・ポスター・パッケージ・家電のデザインなどにも広く用いられており、無意識のうちに目にしている比率なのです。

黄金長方形とは？──美しさが繰り返される不思議な形

黄金長方形とは、その縦と横の長さの比が黄金比（1:φ）になっている長方形のことです。

この長方形には、非常に特徴的で美しい数学的性質があります。

それは、内部に正方形を切り出したとき、残った部分が再び黄金長方形になるという点です。

たとえば、黄金比の比率 a : b（長辺 : 短辺）を持つ黄金長方形から、短辺 b を一辺とする正方形を取り除くと、残った長方形も同じ黄金比の比率 a – b : b を持ち、また新たな黄金長方形になります。

再帰構造としての黄金長方形

この操作を何度も繰り返していくと、どんどん小さな黄金長方形が連続的に現れます。このように、同じ構造が縮小されながら繰り返される形を再帰構造（recursive structure）と呼びます。

下の図は2辺の比が黄金比 a：b となる黄金長方形です。

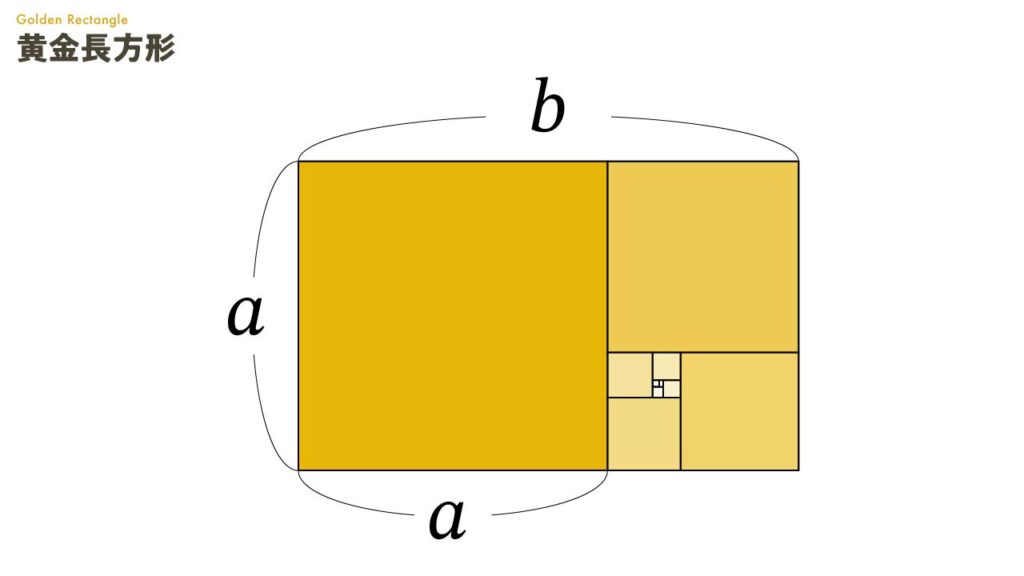
黄金比 a : b に従う黄金長方形から、縦横が等しい a × a の正方形を切り取ると、残された部分も再び黄金比の長方形になります。

この新しい長方形に対しても、同じように正方形を切り取る操作を繰り返すことができ、無限に続く再帰構造が形成されます。

黄金螺旋──数の中にひそむ自然のかたち

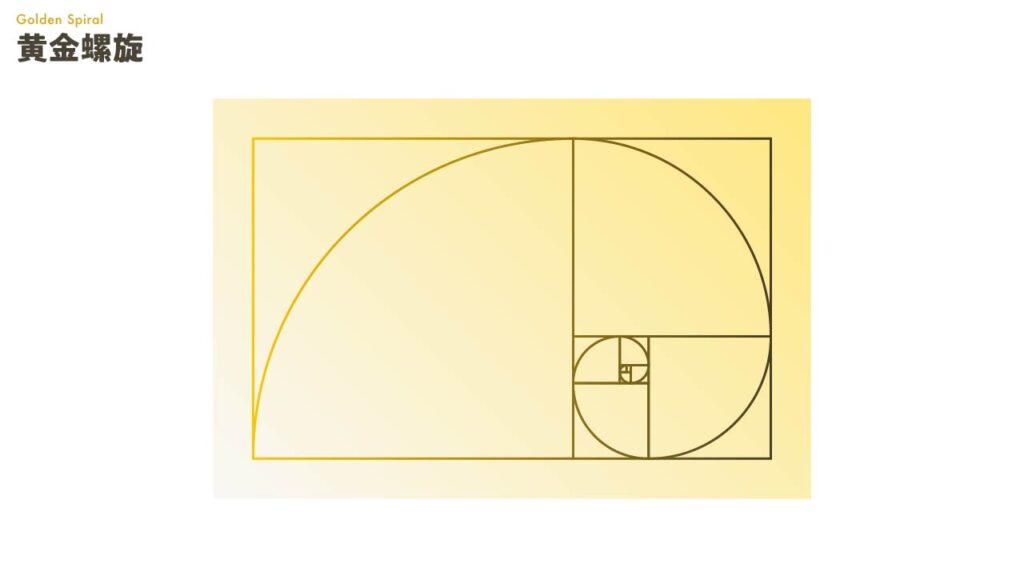
このようにして順に切り取った各正方形の対角に、四分円のような曲線を描いていくと、やがてそれらが連なって、中心に向かって渦を巻く「黄金螺旋（Golden Spiral）」が現れます。

この螺旋は、貝殻の形状や植物の花びらの配置、銀河の渦など自然界のさまざまな場所で見られるものによく似ています。黄金螺旋は、数学的な調和の美と自然界における秩序の象徴として、多くの芸術家や建築家にも影響を与えてきました

フィボナッチ数列と黄金比──自然が描く数学の調和

黄金比と深い関係を持つものに、フィボナッチ数列があります。

この数列は次のように始まります：

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

フィボナッチ数列の特徴は、「前の2つの数を足すと次の数になる」という単純な規則にあります。

黄金比との関係性

この数列の隣り合う項の比（たとえば 13 ÷ 8, 21 ÷ 13 など）を取っていくと、その値は次第に黄金比 φ ≒ 1.618… に近づいていきます。

つまり、フィボナッチ数列は黄金比に“収束する”性質を持つのです。この数学的な関係は、計算上だけでなく自然界にも現れています。

自然界に現れるフィボナッチと黄金比

フィボナッチ数列や黄金比は、以下のような自然の構造や形にも現れます：

• 葉の配置（葉序）や花びらの数
• ヒマワリの種の螺旋
• 松ぼっくりの鱗片の配列
• 貝殻の渦巻き（特に黄金螺旋に似た形状）

これらは、成長効率やバランスに優れた自然の最適化の結果と考えられており、数学的な規則が自然の美しさを生み出していることを示す好例とされています。

黄金比の歴史──ギリシア数学から近代へ

“比”は古代ギリシア数学における重要な概念のひとつです。その中でも、特に美と調和の象徴として知られるのが黄金比です。

現在でこそ「黄金比（golden ratio）」という呼び名が一般的になっていますが、この言葉が登場したのは近代以降のことです。

古代ギリシアの数学者たちは、この比を「外中比（extreme and mean ratio）」と呼び、ユークリッドの『原論』の中にもこの名称で登場します。ユークリッドは「ある線分を外中比によって分割する」と述べ、その性質を幾何学的に定義しました。

やがてルネサンス期の数学者や芸術家たちがこの比に再び注目し、「神聖な比（divina proportione）」や「黄金の比（goldene Schnitt）」といった名称で称えるようになります。

これが現代の「黄金比」という呼び名につながっていきました。

まとめ

黄金比は、単なる数式や幾何学の話にとどまらず、自然界・芸術・デザインに通じる「美と調和の象徴」として、今もなお多くの人を魅了し続けています。

古代ギリシアの知恵からはじまり、フィボナッチ数列や黄金螺旋などを通じて自然とつながるこの比率は、数学と美が交差する地点とも言えるでしょう。

私たちの身の回りにある美しいものに、黄金比が潜んでいるかもしれません。ぜひ、日常の中にもそのかたちを探してみてください。