3.プトレマイオスの天動説とコペルニクスの地動説｜ガリレオ裁判

天動説（地球中心説）と地動説（太陽中心説）

西洋における地球中心説の意味

これまで伝記などで書かれてきたガリレオ裁判についての記述には大きな誤解があるように思います。その最大の理由は、地動説であるコペルニクス説と天動説であるプトレマイオス説が、どんな説であったかが正確に捉えられていないからです。その前にまず、地動説と天動説という用語について注意しておきます。この用語は日本独特のもので西洋では、地動説を太陽中心説、天動説を地球中心説と呼びます。この日本語訳を作ったのは江戸時代の学者志筑忠雄(しづきただお)です。日本の寺や神社は森や山の中、鬱蒼とした自然の中に溶け込むように建っていますが、西洋の教会ははっきりとその存在を目立たせ、自然を支配するかのように建っています。日本の場合、太陽が中心でも、地球が中心でも、どちらも自然が中心なので、2つの語の違いがはっきりしません。「大地が動く」と「天が動く」の方が、違いがはっきりとします。一方西洋では、地球中心説は宇宙を支配するのは人間であるとする由緒正しい一神教を表し、太陽中心説は太陽や月や惑星が人々を支配するオリエント由来のいかがわしい多神教ではないかと疑われてきました。

単純地動説を採れなかった理由

地動説（太陽中心説）というと、自転（日周運動）と公転（年周運動）の場合があります。ガリレオが天体観測をしていたころは、コロンブスがアメリカ大陸を発見してから100年以上経ちますから、地球は球で宙に浮かび自転しているとほとんどの人は認識していました。したがって以下では、地動説とは地球が太陽のまわりを公転しているという説とします。現在の皆さんは、惑星が円軌道ではなく楕円軌道を描いていると知っていると思います。説明の都合上、惑星が太陽のまわりを円軌道を描いて周(まわ)っているという説を“単純地動説”と呼ぶことにします。一般の大衆にとっては、円軌道でも楕円軌道でもかまいませんが、当時の天文学者は単純地動説を採るわけにはいかなかったのです。その主な理由は、円軌道では、春、夏、秋、冬の期間の長さが違うことの説明がつかないからです。キリスト教会は、暦を設定するという重要な役割を負っていたからです。（詳しくは〔暦の起源〕第12回 中世ヨーロッパの暦 : アルマナックの普及 参照。）

以下で、コペルニクス説とプトレマイオス説について解説します。

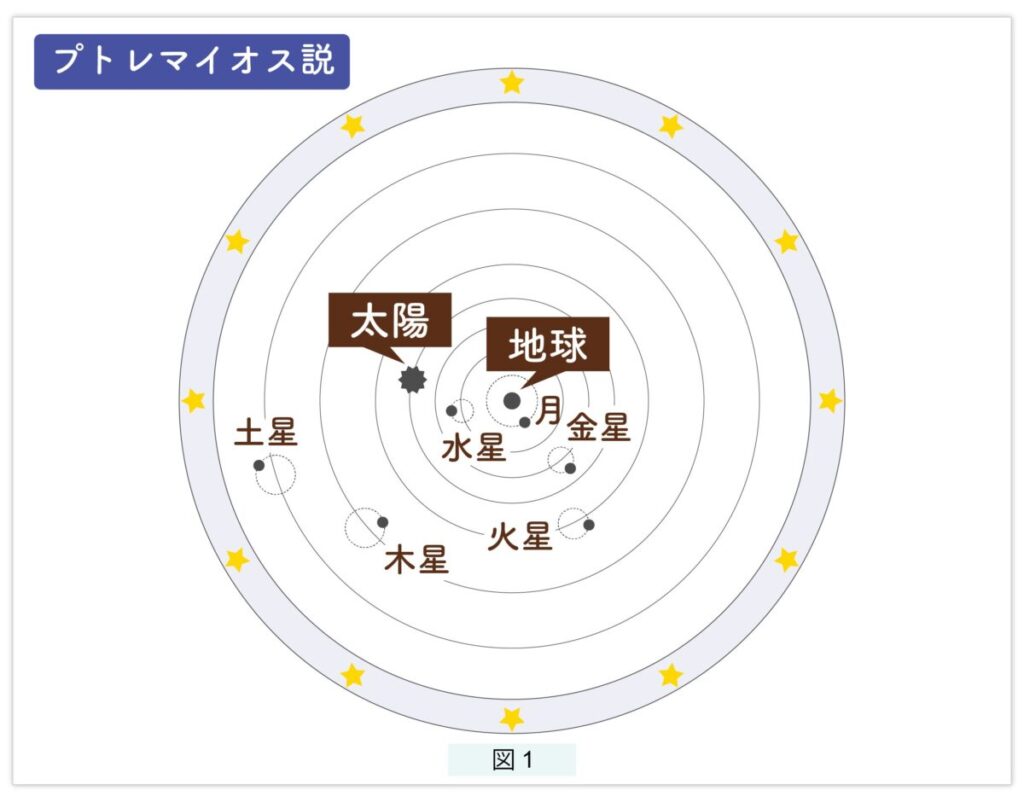
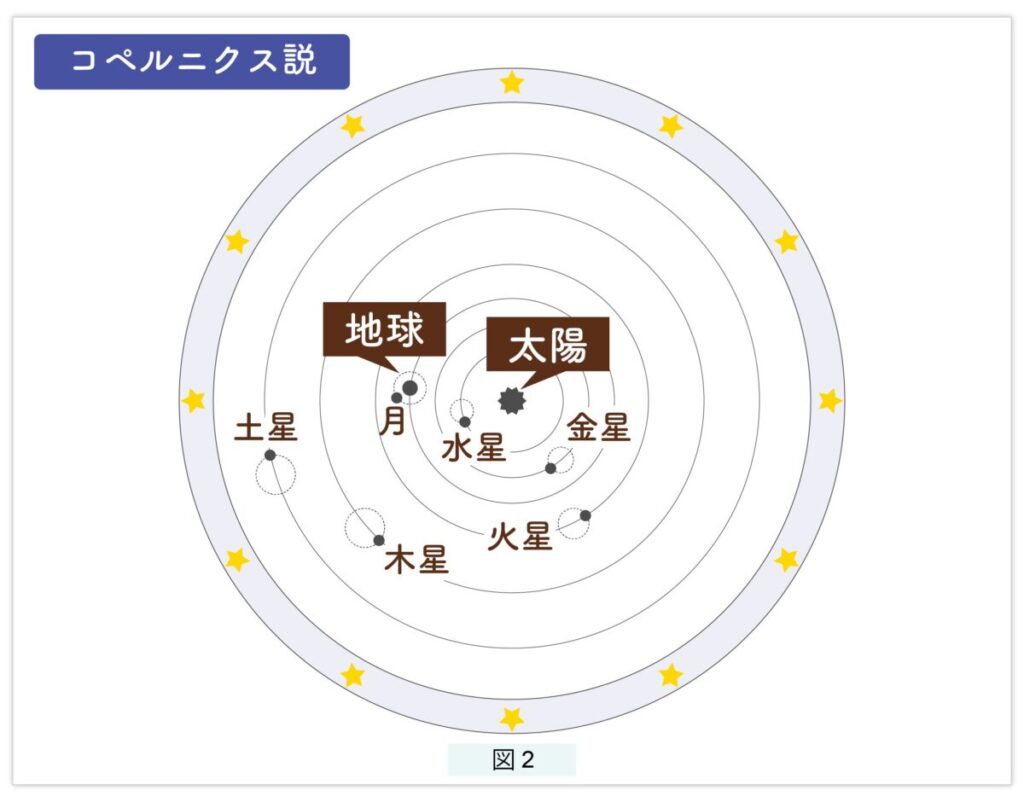
天球モデル

天球とは 〜 太陽、月、惑星の観測 〜

古代の人々は、星々は大きな球に貼りついていて、球が地球のまわりを回転していると考えていました。この仮想的な球を天球といいます。毎晩南の空を観察していると思ってください。太陽、月、惑星以外の星々は天球に貼りついていて動きません。天球は1日1回転します。単純化して考えると理解しやすいため、1年は360日とし、地球は24時間で1回転するとします。天球を固定したいのですが、自転を止めるわけにはいかないので、地球が1回転するごとに南の空を観察するとします。すると空（天球）は止まって見えます。

太陽の動く道

ある日の夜 0:00 に南の空を観測していたとします。次の日の 0:00 も南の空はほとんど同じですが、少しだけ違っています。公転しているからです。1年を360日としましたから、天球は1日に1度だけ西に動いているのです。1日＝24時間＝4×360分 ですから、1度動くのに4分かかります。したがって南の空が同じだったのは、その日の 4分前の11:54 なのです。毎日4分ずつ時間を早めて観測することにします。すると、空は毎日同じになります。1日4分ですから30日で、30×4分＝2時間、90日で6時間となります。つまり90日後は午後6時に同じ空を見ています。午後6時は、西の空に夕日が沈むところです。さらにあと90日観測することにします。お昼ですからもう星は見えませんが、同じ星が輝いていると考えてください。90日前から振り返ると、夕方の6時に西の空にいた太陽がお昼の12時に真南に来ていますから、太陽はこの不動の星空の中を西から東へ移動したことになります。この太陽の通る道を黄道といいます。月も惑星もだいたいこの道を通ります。実際には少しこの道を外れるので、惑星が通る帯を獣帯といいます。

プトレマイオスの周転円モデル

外惑星「惑う星」の動き

図2で、地球より内側の惑星、水星と金星を内惑星、外側の惑星、火星と木星と土星を外惑星といいます。もう1度、南の空を観測していると想像しましょう。太陽は1年に1周、月は1ヵ月に1周、西から東へと移動します。内惑星はあとまわしにして、外惑星を観察しましょう。外惑星も太陽と同様、太陽よりもゆっくりと移動しますが、太陽とは異なる奇妙な行動をします。通常は太陽と同じように西から東へ移動するのですが、あるとき動きがだんだん遅くなり、しばらく動きが止まったかと思うと、こんどは逆に西に向かって移動し始めます。逆行を何日か続けたのちに、また通常の移動に戻ります。この奇妙な行動のため、惑星は“惑(まど)う星”といいます。

惑星の動きは周転円モデルで説明できる

この現象を説明するために、2世紀前半にアレクサンドリアで活躍した天文学者プトレマイオスは、周転円というモデルを考え出しました。図3 のように地球 E を中心とした円を考えます。この円を導円と言います。惑星 P はこの導円上の点 O を中心とした小さな円上にあります。この小さな円を周転円と言います。

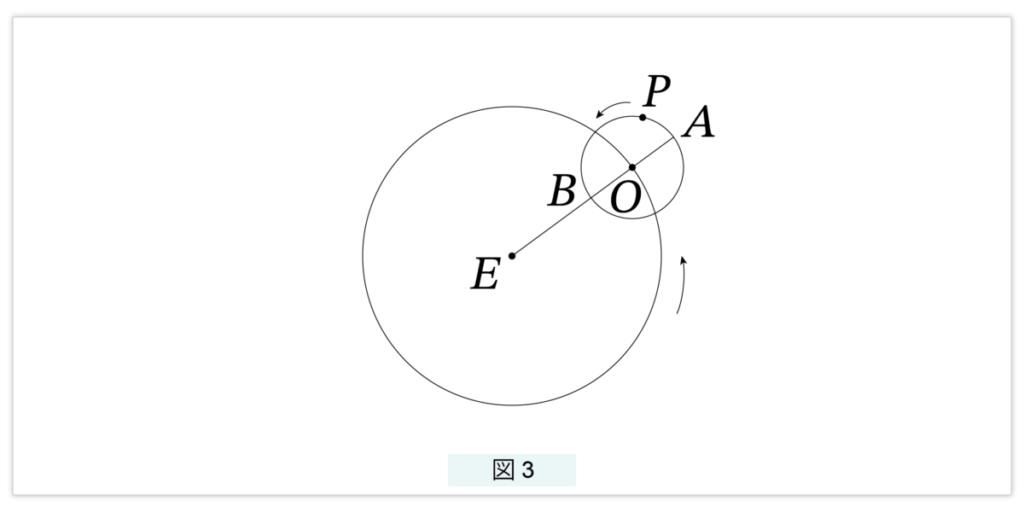
惑星 P は周転円を反時計回りに回転しますが、周転円の中心 O も地球の周りを反時計回りに回転します。地球の反対側の点 A のあたりに来た時が順行で、地球側の点 B のあたりが逆行です。この周転円モデルによって、惑星の奇妙な振る舞いがうまく説明されます。ここでは説明を省略しますが、内惑星の振る舞いも、この周転円モデルで説明がつきます。

プトレマイオスの離心円モデル

惑星の軌道は楕円である

もう一つ重要なことは、実際の惑星の軌道は、円ではなく楕円だということです。教科書などで描かれ楕円軌道は誇張されているものが多いですが、実際は、ほとんど円に近い楕円です。最もひしゃげている火星の軌道でも、半径10cm ぐらいの円をコンパスで描いてみると、実際の楕円軌道はこの円の鉛筆の線の太さほどひしゃげたものとなります。惑星 P が太陽 S のまわりを回っているとします。すると、P と S の距離が最も短い近日点と最も遠い遠日点とができます。近日点の近くでは速度が速く、遠日点の近くでは速度が落ちます。昔は時計などないので、1日の長さが短くても長くても影響はありませんが、1ヵ月となると問題が生じます。3ヵ月にもなると2日もずれることがあるので、月が星座のどの位置にあるかの測定とか、満月の日とか春分の日の測定などに支障が出てきます。

離心円（エカント）とは

プトレマイオスは、これを離心円というモデルを設定することで解決しました。

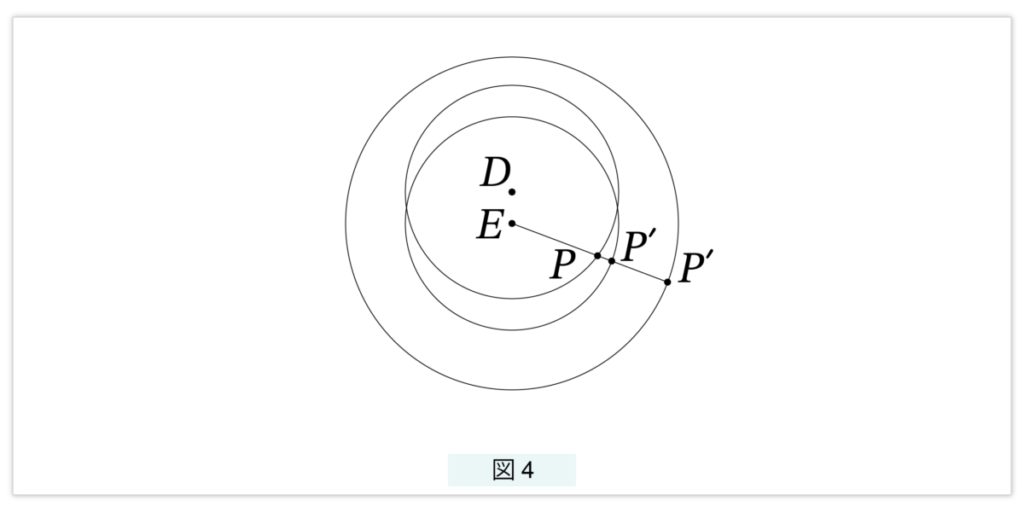
図4 を見てください。太陽 P は小さな円 D のまわりを回っています。E が地球です。地球は太陽の軌道の中心 D から離れたところにあるので、円 D を離心円（エカント）と言います。太陽 P は離心円上を回っていますが、地球から見ると太陽は E を中心とした円を回っているように見えます。図4では、E を中心とする円が2つ書かれていますが、どちらでもかまいません。つまり半径の長さは任意です。この円の一つを円E と呼びます。円E が黄道です。星々や太陽は遠いところにあるので距離ではなく E から見た角度で判別します。つまり、離心円上を動く P は黄道上を動く P’ として認識します。したがって、太陽や星の速度は“角速度”で測ります。これまで恒星の角速度は1日約1度としていましたが、ここではもう少し正確に

1日当たり 360/365.25 度

とします。これは P が円 D を回る角速度で、つねに一定です。しかし P’ が円 E を回る角速度は一定ではありません。A の近くでは速く、B の近くでは遅くなります。

「季節の長さの違い」の解釈

図5 を見てください。E は地球で、太陽は D を中心とする小さな円を回ります。太陽が最も地球に近づくのは A で、近日点といいます。最も遠さがるのは B で、遠日点といいます。しかしこれは季節とは関係がありません。現在では、冬の方が地球は太陽の近くにいますが、毎年ほんの少しずつ変化します。季節は地軸の傾きによって決まります。

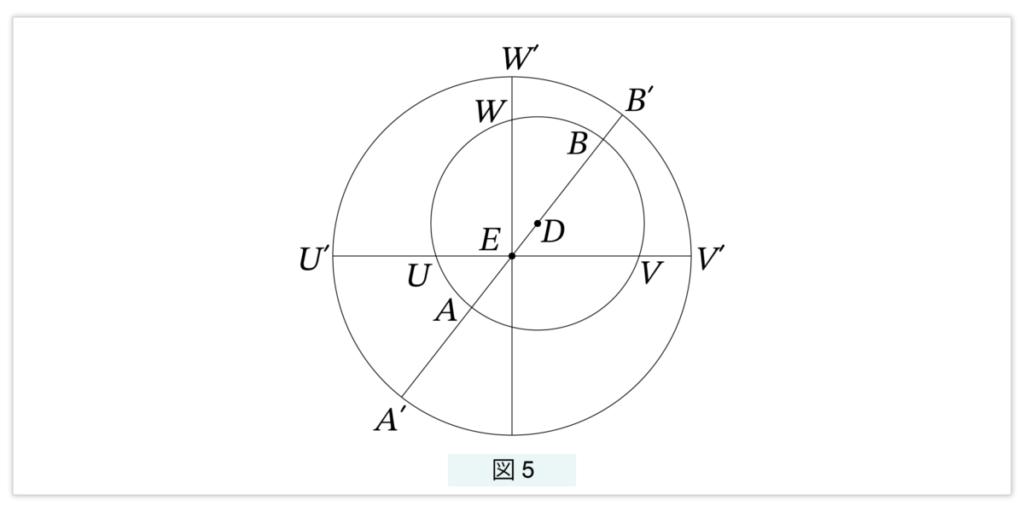
図5 では E を地球で、地球のまわりを回っているのは太陽だとしていますが、立場を入れ替えて、E を太陽で、太陽のまわりを回っているのが地球であると考えることもできます。実際は、ED を長軸、E を焦点とする楕円軌道ですが、これを外側の円で近似しています。太陽は V, W, U と移動しますが、人間の目には円軌道の V’, W’, U’ を移動しているように見えます。離心円というモデルは楕円軌道のよい近似となっているのです。

点 V, W, U はそれぞれ春分点、夏至点、秋分点です。春分の日から夏至までが 94.5日で、夏至から秋分の日までが 92.5日です。プトレマイオスは、この値をもとに ∠VED ＝ 65°30’ であることを計算しました。この値は毎年少しずつ変化します。この変化を春分点移動といい、春分点移動はバビロニア時代から問題となり、厳密に測定されてきていました。

コペルニクスの地動説とは

コペルニクス説は周転円モデルである

コペルニクスはこの離心円（エカント）という考えに猛反発しています。「神は、完全で完璧な宇宙をお創りになったはずだ。中心のずれたエカントなどありえない」と考えました。幸いエカントは周転円で簡単に実現できます。図4 で内側の円 E の半径は円 D と同じとし、これを導円とします。図6 参照。

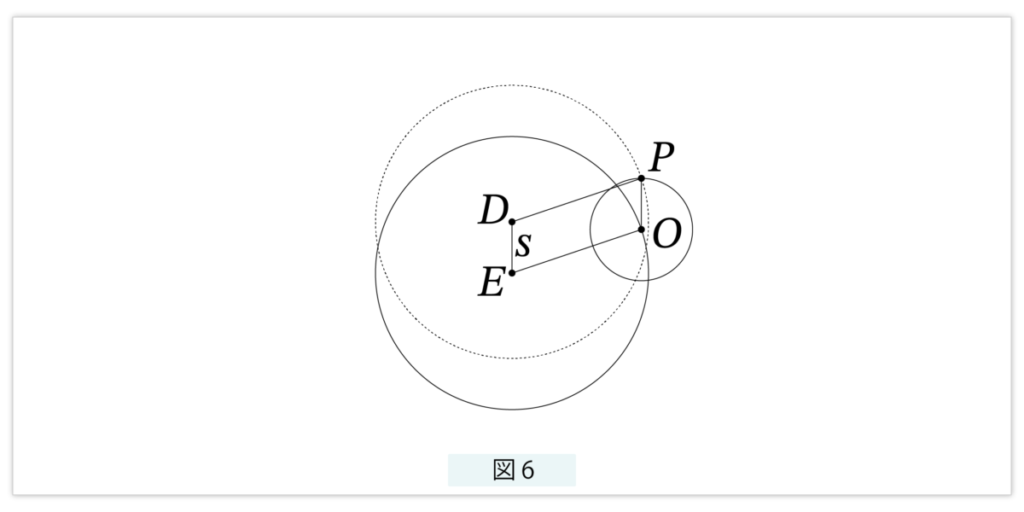
ED＝s とし、この導円上の点 O を中心とする半径 s の円周上を、Pは回転します。O が円 E を一周すると、Pも周転円上を一周します。四角形DEPP が平行四辺形になるように動くとすると、点 P が描く軌跡は図4 の点 P と同じになります。コペルニクスは、E を太陽、P を地球としています。太陽を中心にして、地球を含めすべての惑星が周転円を回るようにしたものがコペルニクス説です（この節の初めに述べた図2 参照）。コペルニクス説は単純地動説ではありません。図2 から周転円を取り除いたのが単純地動説であり、コペルニクス説はプトレマイオス説と同じで、周転円モデルなのです。

ティコ・ブラーエ説

ガリレオがスケッチしていますが、金星は月と同じように満ち欠けし、大きさも変化します。ガリレオはこれを地動説の証拠として述べています。この事実は、プトレマイオスの周転円でも説明できますが少し欠陥があります。周転円モデルでは、金星は常に地球と太陽の中間にありますから、月の場合の満月に対応するものがありません。しかし、この発見はガリレオが最初ではなく、ケプラーの雇い主ティコ・ブラーエのものです。次に示す 図7 がティコ・ブラーエ説です。

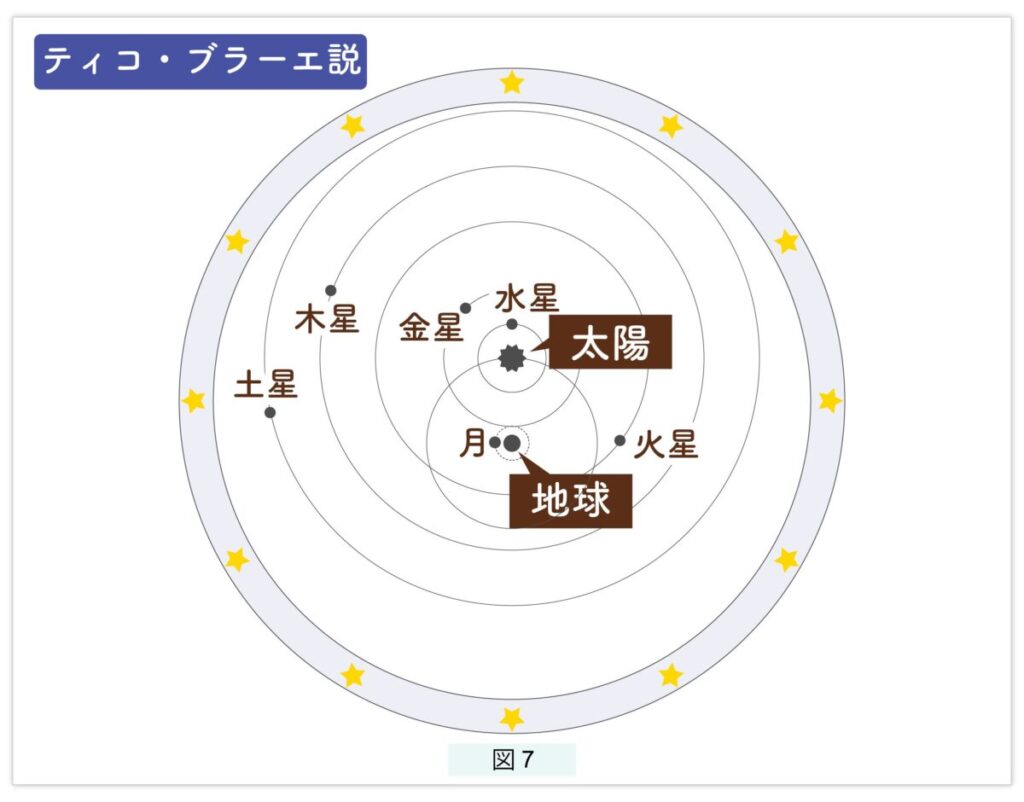
ガリレオはケプラーとも文通していますし、当然知っていたはずですが、ティコ・ブラーエのことはいっさい言及していません。ティコの説では、金星と水星が太陽の衛星となります。また、火星、木星、土星は太陽のまわりを回っていますが、太陽が地球の周りを回っていますから、ティコの説は“地球中心説”となります。

コペルニクス説は単純地動説ではない

これまでいろいろな著作で、コペルニクス説になって太陽系のしくみが簡潔になりすっきりした、と述べられていますが、これは誤りです。おそらくコペルニクス説を、単純地動説と勘違いしているのだと思います。太陽と惑星との関係は、上で述べた「逆行現象」と「楕円軌道」が主なものですが、それ以外にもいろいろあり、コペルニクスの時代には、周転円を中心にさらに周転円が回る、といった複雑怪奇なものになっていました。コペルニクスはこれを単純化したいと考えたのでしょうが、あまり成功しなかったようです。