タレスの定理 とは

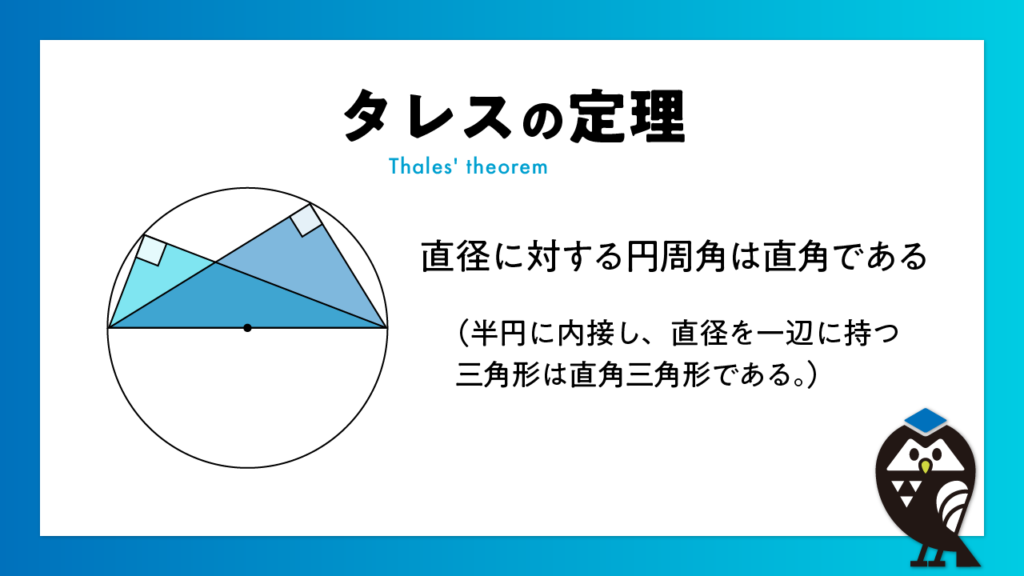
タレスの定理とは？──円と直角の不思議な関係

タレスは古代ギリシアの数学者で、図形の性質を初めて“証明”した人物として知られています。彼が扱った定理のなかでもとくに有名なのが、「タレスの定理」と呼ばれる円周角に関する法則です。

それは次のような内容です：

「直径に対する円周角は直角になる」

言いかえると、「円の中に直径を引き、その両端を結ぶ点を円周上に取ると、その3点を結んだ三角形は直角三角形になる」ということです。

これは円と三角形の性質を結びつけた非常に基本的かつ美しい幾何学的事実で、古代において「定理を論理的に導く」という数学的姿勢の出発点ともいえる重要な発見です。

下の図のように直径をABとする円の円周上に点Pをとると、∠APBは必ず90度になります。

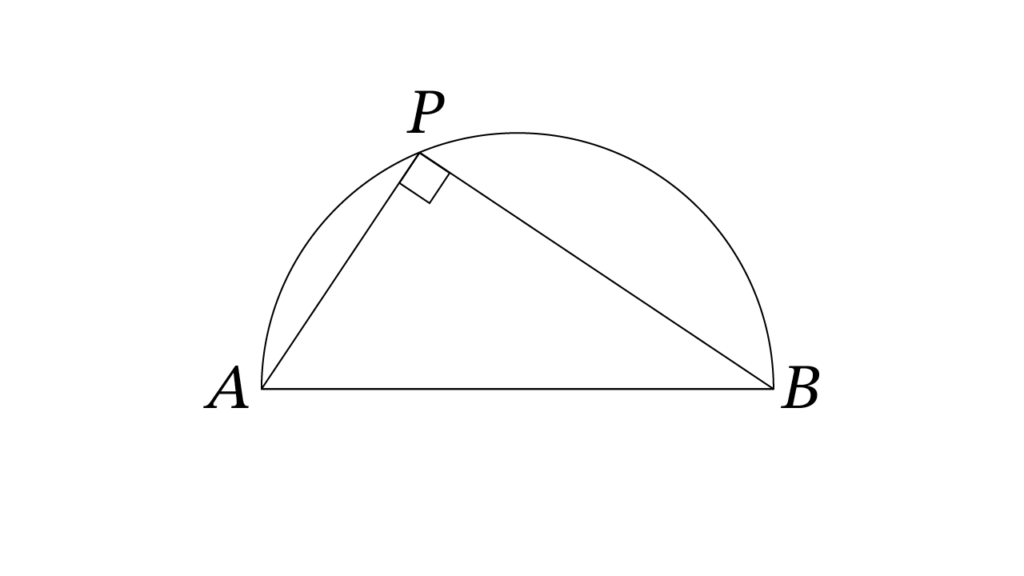
タレスの定理の証明

定理の内容：

「円の直径の両端と円周上の1点を結んだ三角形は直角三角形になる」

すなわち、∠APB = 90° であることを証明します。

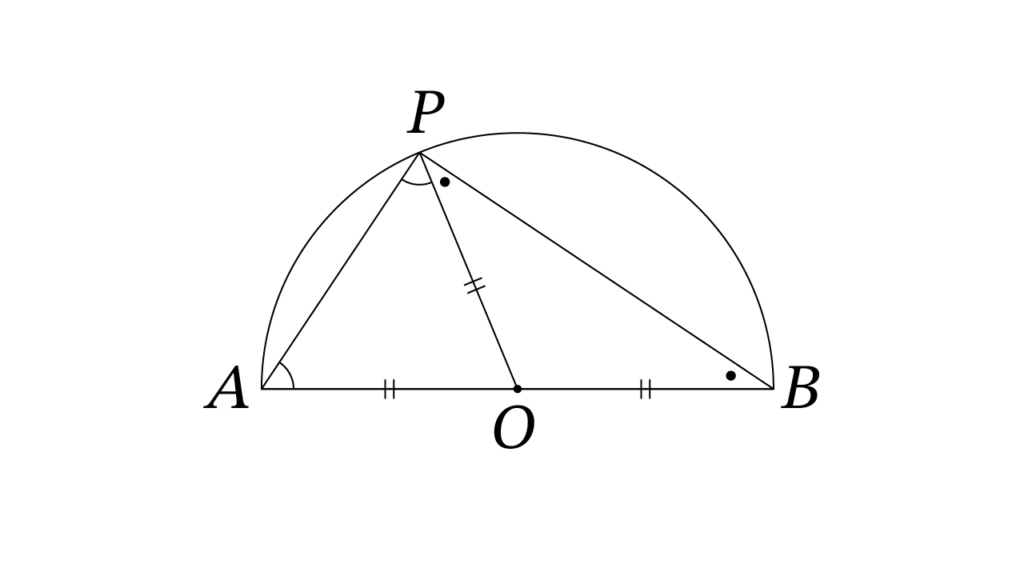
証明の流れ

図のように、点 O を円の中心とし、点 P を円周上の任意の点とします。直径 AB の両端と点 P を結んで三角形 APB を作ります。

また、点 P と中心 O を結んで補助線を引きます。

すると、

OA = OP = OB

となり、三角形OAPと三角形OBPは二等辺三角形となります。

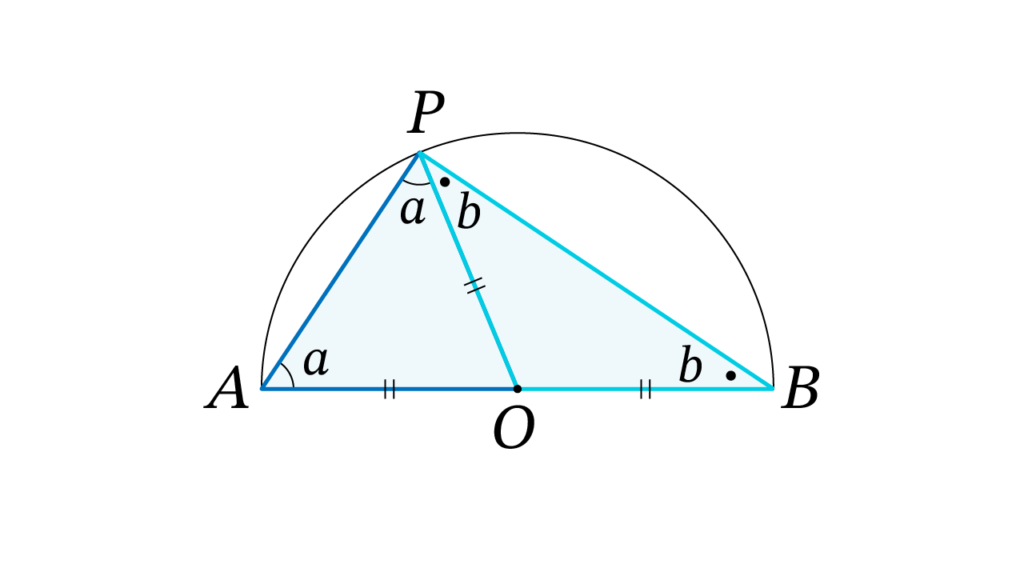
二等辺三角形の底角は等しいので

∠OAP = ∠OPA = a
∠OBP = ∠OPB = b

三角形PABの内角の和より

a + a + b + b = 180°
2a + 2b = 180°

よって a + b = 90° となり、∠Pは直角です。

この他にも、彼は以下を証明したと言われています。
・円はその直径で二等分される
・二等辺三角形の底角は等しい
・対頂角は等しい

これらの定理の内容はタレスよりも以前から知られていました。タレスよりも1000年以上前、古代バビロニアでは高度な数学が発達していたのです。

タレスとはどんな人物？

タレスは、紀元前6世紀ごろに小アジアのイオニア地方、ミレトス（現在のトルコ西部）で活躍した哲学者・数学者・天文学者です。

古代ギリシアで最も古い自然哲学者の一人とされ、**「ギリシア七賢人」**にも数えられています。

タレスは、世界の成り立ちについて「万物の根源（アルケー）は水である」と考えました。これは神話的な説明に頼らず、自然の中に法則や原因を求めようとした、哲学的思考の出発点として重要な意味を持ちます。

また、タレスはエジプトで学んだ知識をギリシアに持ち帰ったとも言われており、数学や天文学における理論的な推論の基礎を築いた人物でもあります。

とくに図形の性質を「証明」によって導いたという点で、後の数学の発展に大きな影響を与えました。

タレスの影響を受けた人物の一人、ピタゴラスのお話はこちらから▼
古代ギリシアの数学者ピタゴラスのお話[Vol.1]

また、タレスはエジプトを訪れた際にピラミッドの高さを影の長さを利用して測定したと伝えられています。

まとめ

タレスの定理は、三角形と円の深い関係を示すと同時に、「図形の性質を論理的に説明する」という数学の本質を体現する定理でもあります。

タレスが残したこの定理は、単なる図形の性質を超えて、証明によって真理に迫るという思考の重要性を教えてくれます。

2000年以上経った今でも、数学を学び始めた人々が最初に出会う定理のひとつであり、論理的思考の原点として今なお輝き続けています。